Бусыгин Б.С., Коротенко Г.М., Коротенко Л.М. Введение в современную информатику

Подождите немного. Документ загружается.

290

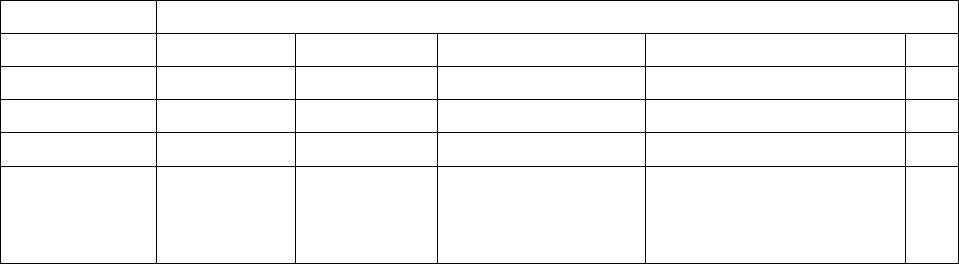
8.19. Моделирование в циклических вычислениях некоторых

типовых выражений

В циклических процессах очень часто используются некоторые

выражения, которые имеют стандартные алгоритмические реализации. К ним

можно отнести следующие:

(–1)

(8.8)

(8.9)

!2!)2( nn =

(8.10)

Все они зависят от элементов натурального ряда чисел:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, ... , n

Как правило, сокращённо, изменение значений натурального ряда на

отрезке [1,n] записывают так:

1, 2, ... , n

В зависимости от изменения значений элементов ряда n, вышеуказанные

выражения принимают соответствующие значения (табл. 8.42). При этом и ряд

можно рассматривать как выражение, значение которого изменяется в

соответствии с изменением номера элемента n.

Таблица 8.42

Изменения значений выражений в соответствии с изменением значений,

которые подставляются в них

Выражение

Изменение значений выражения

…

(–1)

= –1

(–1)

= +1

(–1)

= –1

(–1)

= –1

…

1!=1

2!=1·2=2

3!=1·2·3=6

4!=1·2·3·4=24

…

!2!)2( nn =

2!=2

4!=24

6!=

1·2·3·4·5·6=

=720

8!=1·2·3·4·5·6·7·8=

=40320

…

Значение выражения (–1)

можно моделировать двумя разными

способами:

 на каждом шагу приформировывать унарный знак "–" к предыдущему

значению переменной, сохраняющей значения (–1) или (+1);

 на каждом шагу умножать предыдущее значение (–1) или (+1) на (–1).

Вместе с тем, следует помнить, что для выполнения приформировывания

знака или умножения на (–1) необходимо предварительно извлекать число из

перменной на сумматор, проводить требуемые действия, а потом засылать их

назад в переменную.

Первые пять строчек значений этих функций, которые будут выведены на

экран программой и текст самой программы приведены на следующей

странице.

291

(–1)

2n!

1 –1.0 1.0 2 2.0

2 1.0 2.0 4 24.0

3 –1.0 6.0 6 720.0

4 1.0 24.0 8 40320.0

5 –1.0 120.0 10 3628800.0

{Программа моделирования значений функций (8.8), (8.9), (8.10)}

Var

med1, med2, Factor1, Factor2 : Real;

n, n2, I : Word;

Begin {Инициализируем начальные значения переменных}

med1 := –1; {Имя переменной, принимающей значения (–1)}

med2 := –1; {Имя переменной, принимающей значения (–1)}

Factor1n := 1; {Имя переменной, принимающей значения

}

Factor2n := 2; {Имя переменной, принимающей значения

!2n

}

n := 1; { Имя переменной, принимающей значения n}

n2:= 2; { Имя переменной, принимающей значения 2n}

{ Фактически присваиваем переменным значения выражений}

{ при n = 1, которое моделирует значения переменной n.}

{ Переменную 2n моделирует значение переменной n2.}

{Ограничиваем действие цикла с предусловием значением n=40,}

{что эквивалентно максимальному значению n1=40}.

{}

Writeln ('Значения переменных=', med1:8:1,

med2:8:1, n:3,

Factor1n:8:1, n2:3, Factor2n:8:1);

while n <= 40 do Begin

med1 := –med1;

med2 := (–1)*med2;

n:= n + 1;

Factor1n := Factor1n * n;

n2 := n2 + 2;

Factor2n := Factor2n * (n2–1) * (n2);

Writeln ('Значения переменных

=',

med1:8:1, med2:8:1, n:3,

Factor1n:8:1, n2:5, Factor2n:11:1);

end;

end.

Очень важным моментом является процесс отображения циклического (то

есть последовательного) добавления некоторых данных к значению

определённой переменной. Допустим, необходимо вычислить выражение

Y = A+5, при значении А=2.

292

На языке ТП это выглядит так:

А := 2;

Y := A + 5; {Стало Y = 7}

Однако, если нужно добавить к значению, которое находится в

переменной Y ещё какие-либо значения (допустим 8 и 10), это будет выглядеть

так:

Y := Y + 8; { Становится Y = 15}

Y := Y + 10; { Становится Y = 25}

……………………… {и так далее}.

Выражение Y := Y + 10 для компьютера указывает, что необходимо:

 взять предыдущее значение, находившееся в переменной Y;

 сложить его с постоянной 10;

 заслать новое значение на старое место в переменную Y.

Другой пример. Допустим необходимо вычислить выражение:

zyxf coscoscos ++=

На языке ТП оно может быть записано следующим образом:

f := cos (x) + cos (y) + cos (z).

Тогда встроенной функцией cos(х) будут вычислены три значения

косинусов от соответствующих аргументов x, y, z, а потом, после

суммирования этих трёх значений, сумма будет заслана в переменную f и

заменит там предыдущее значение. Однако, если это же выражение вычислять в

цикле, то необходимо предварительно очистить переменную f, а потом

проводить прибавления на каждом шагу. Очистка содержимого переменной f

выполняется засылкой в неё нулевого значения. Соответствующиий код может

выглядеть так:

.....................

f := 0;

f := f + cos (x);

f := f + cos (y);

f := f + cos (z);

.............. ....

В результате выполнения этой последовательности команд получим

результат, соответствующий вычисленному в вышеприведенном выражении.

Упражнения

1. Вычислить с помощью цикла с параметром for значения конечной

суммы S для выражения:

∑ ∑

= =

−+−=

332

.)1()1(

n n

nnS

Проведите исследование работы программы с помощью дебаггера.

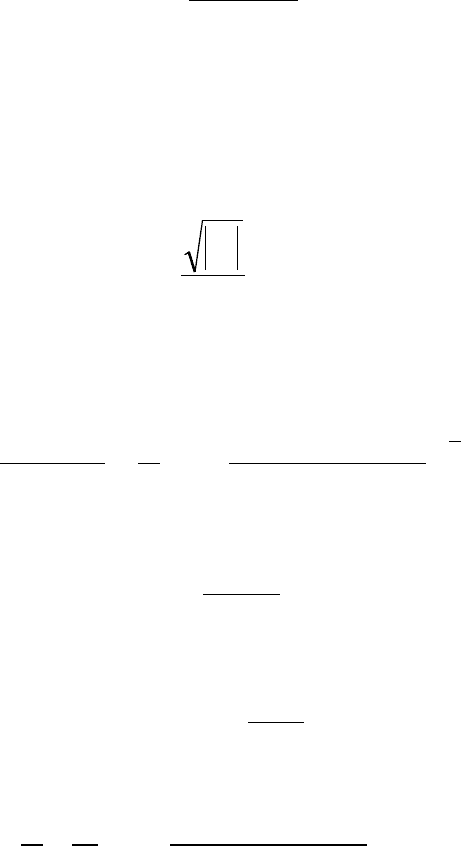
293

2. С использованием оператора цикла с предусловием while напишите и

выполните программу табулирования значений функции y с действительным

аргументом x = 0.25 на отрезке измененя n [1, 5]. Проведите исследование

работы программы с помощью дебаггера.

3sin

−

3. С использованием оператора цикла с послеусловием

repeat напишите

и выполните программу табулирования значений нижеприведенного

выражения функции y с действительным аргументом на отрезке изменения n [1,

7] при х= –9. Проведите исследования работы программы с помощью дебаггера.

y =

4. С использованием оператора цикла с предусловием

while напишите и

выполните программу табулирования значений нижеприведенных функций:

∑

∞

−

−−

−

)!2(

)12()1(212

)(csc

∑

∞

−

∑

∞

−=

)1(

∑

∞

+−

=−

)14)(14(

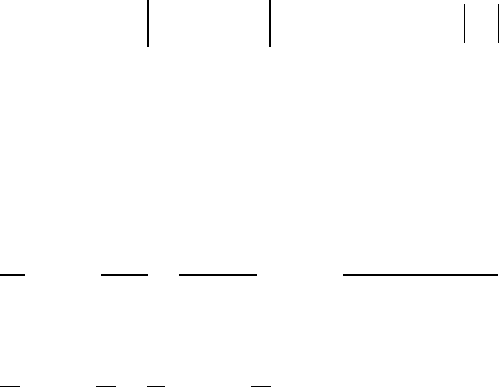
294

8.20. Особенности вычисления бесконечных сумм. Организация

итерационных процессов с помощью циклов

while и repeat

Одним из наиболее распространённых алгоритмических процессов

является математическое действие прибавления. В простых случаях сумма

выглядит обычно так:

С = А + В.

Однако в более сложных случаях сумма выглядит совсем иначе, когда

количество прибавляемых элементов заранее неизвестно, а результат стремится

к некоторому пределу по какой либо формуле. Типовым примером

итерационного циклического процесса может быть задача вычисления суммы

бесконечного ряда. Понятие суммы неразрывно связано с понятием сходимости

такого бесконечного ряда. Обычно, ряд значений

...,,...,,

10 n

ttt

называется

сходящимся, если сумма

ttts ...

++=

его первых (n+1) элементов, которые

суммируются при бесконечном возрастании n, стремится к некоторой границе

S, которая и называется суммой ряда, то есть:

∑

∞→

lim

Общий член

ряда, который сходится, при этом стремится к нулю, то

есть:

.0)(lim;0lim

=−=

−

∞→∞→

sst

Таким образом, последовательность

...,,...,,

21 n

sss

является

последовательностью значений, которые мы ищем и определяет следующие

условия завершения суммирования:

εε

≤≤−

− nnn

tилиss

Как правило, суммой нескольких элементов является результат

прибавления очередных значений к сумме всех предшествующих элементов из

этой последовательности.

Математически это записывается с помощью знака суммирования ∑:

∑

∞

⋅⋅⋅⋅

⋅⋅

⋅

321

nn 



(8.11)

∑

∞

++++=



(8.12)

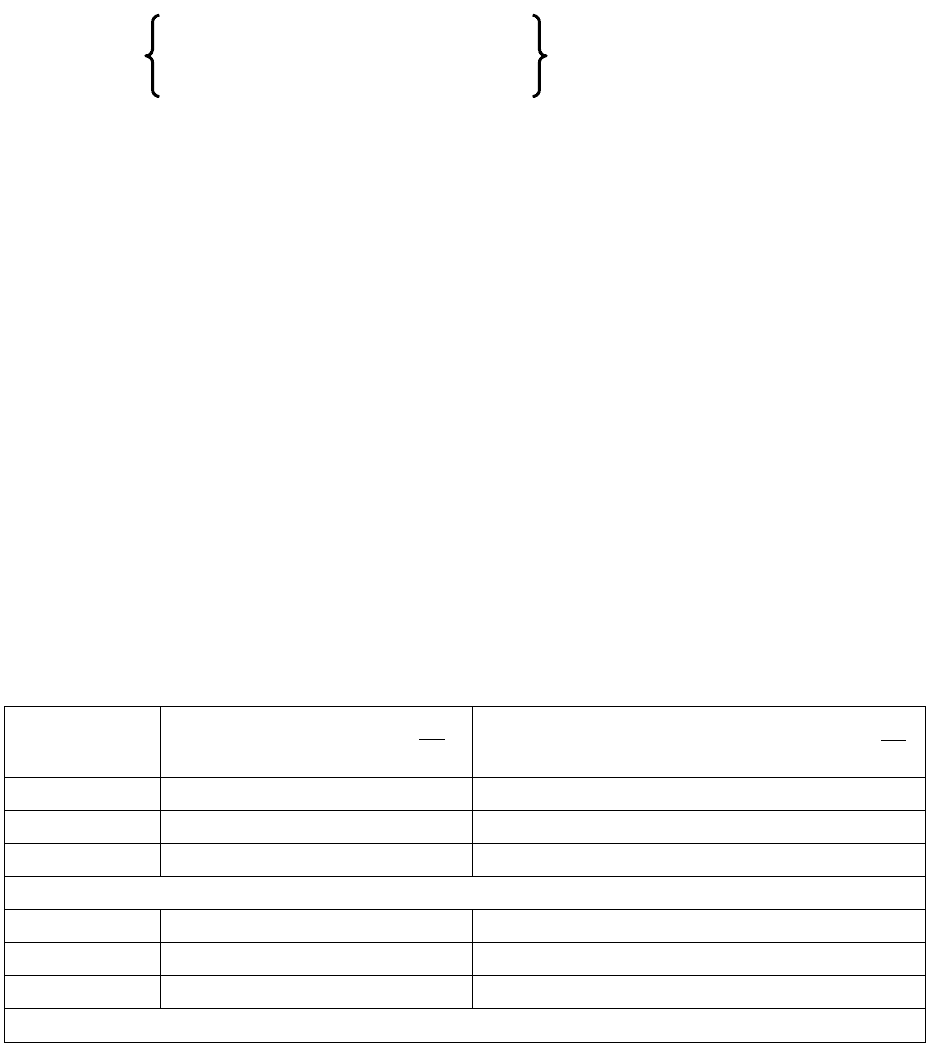
295

Несмотря на простоту записи этого процесса, имеются некоторые важные

обстоятельства для более внимательного рассмотрения того, что происходит

при суммировании элементов бесконечных рядов.

Так, как операции прибавления значений в таких суммах в математическом

понимании нужно выполнять до бесконечности (∞), следует понимать, что в

компьютере такие большие значения, конечно же, обрабатываться не могут. С

другой стороны, как правило, необходимо вычислять конечную сумму с

некоторой точностью. Рассмотрим, что в этом случае имеется в виду.

Когда выполнена определённая часть вычислений, на некотором k-ом шаге

уже имеется накопленная сумма (k-1) елементов и очередной k-й элемент

суммирования (рис. 8.42), который должен быть прибавлен к общей сумме.

Очевидно, что очередной элемент ряда сделает тем меньший вклад в

общую сумму, чем меньше его значение. При этом, если его величина окажется

меньше некоторой достаточно малой постоянной величины (константы)

(например, наперёд заданой величины

ε = 0.0000001 или какой либо другой), он

должен перестать вносить соответствующий вклад в общую сумму и,

соответственно, оказывать влияние на те цифры суммы, которые определяют её

точное значение. Однако, как свидетельствует опыт многочисленных

вычислений, существует ещё ряд факторов, которые влияют на процесс

разработки подобных алгоритмов. Посмотрим внимательнее на результаты

вычисления сумм, представленных формулами (8.11) и (8.12). Оказывается, что

точность (т.е. близость к точному значению) текущей суммы зависит ещё и от

того, насколько быстро увеличивается знаменатель дроби, которая

вычисляется. К примеру, для формулы (8.11) значения компонентов будут

изменяться так (табл.8.43).

Таблица 8.43

Изменение значений компонентов формулы (8.11)

Значение n

Значения элемента

Значения суммы К элементов

∑

1.000000000

1.0

0.500000000

1.5

0.166666666

1.6(6)

.........................................

0.000000275

1.718281801

0.000000025

1.718281826

0.000000002

1.718281828

Примечание: K – количество просуммированых элементов n

=(a

+ a

+ … + a

k-1

)

k-1

∑

n=1

Рис. 8.42. Схема суммирования при вычислениях бесконечных сумм

+ a

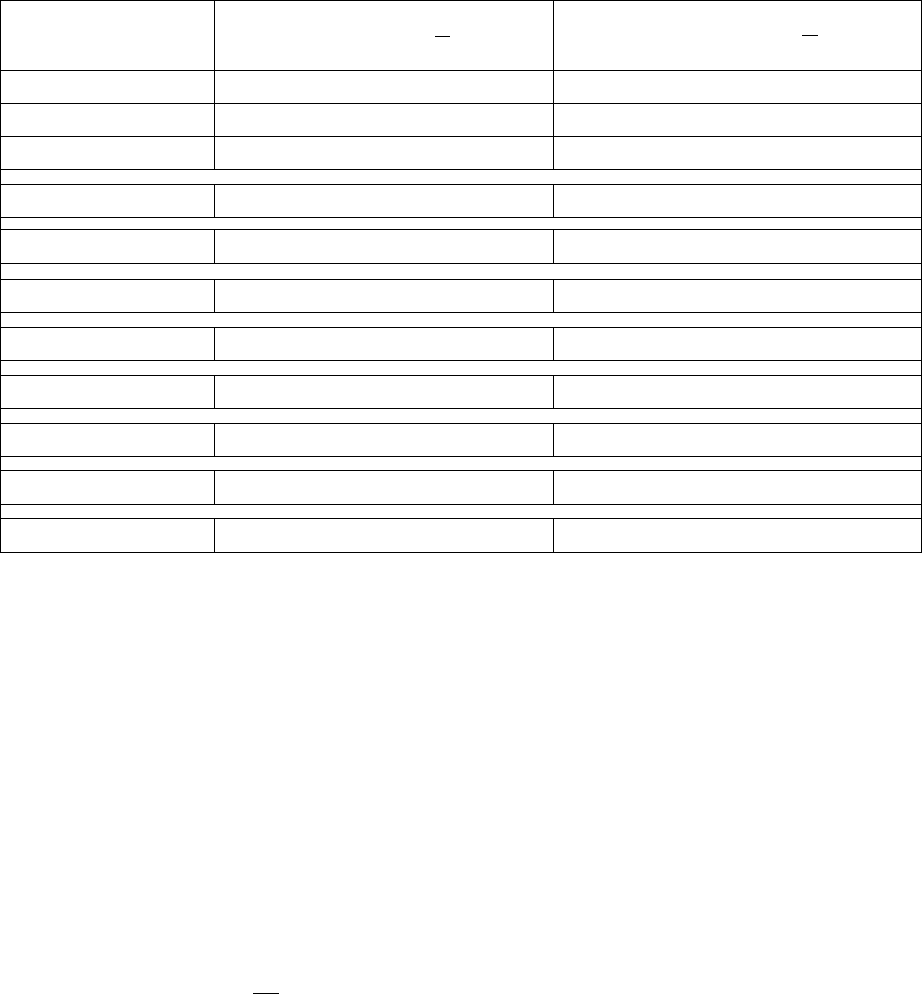
296

Видим, что знаменатель дроби, принимающей участие в выполнении

необходимых действий растёт очень быстро и процесс суммирования сходится

за несколько десятков шагов. Другая картина наблюдается при вычислении

формулы (8.12) (см. табл. 8.44):

Таблиця 8.44

Значения элементов ряда (8.12)

Значения n

Значения

∑

1.0000000

0.5

1.5000000

0.3(3)

1.8333(3)

......................................................................

0.1000000

2.9289683

......................................................................

1350

0.0007407

7.7854450

......................................................................

10224

0.0000978

9.8097577

......................................................................

20000

0.0000500

10.4807282

......................................................................

100000

0.0000100

13.0901461

......................................................................

1000000

0.0000010

15.3927267

......................................................................

5000000

0.0000002

17.0021642

......................................................................

10 000 000

0.0000001

17.6953113

Из таблицы 8.44 хорошо видно, что когда элемент, который прибавляется,

уменьшаетсяся очень медленно, предусмотреть его вклад в общую сумму

достаточно трудно. Поэтому Вы должны иметь ввиду несколько вариантов

алгоритмов, которые могут дать возможность получить необходимый результат

в разных случаях или использовать дебаггер для контроля точности результатов

вычислений.

Посмотрим внимательнее на таблицы 8.43 и 8.44. Очевидно, что для

успешного завершения суммирования элементов первой суммы, достаточно

проверить условие, чтобы очередной элемент ряда был меньше некоторого

малого числа ε (епсилон), которое задаёт сам программист (пользователь).

Величина ε и будет контролировать точность конечной суммы. Другими

словами, (в соответствии с данными таблицы 8.45), если мы сравним значения

очередного элемента

с ε = 1е-6 (так записывается в ТП число 0.000001), то

получим значения суммы с точностью приблизительно 6 знаков после точки.

При сравнении значения этих же елементов с ε= 1е-7, точность увеличивается,

и так далее (табл. 8.45).

297

Таблица 8.45

Зависимость значения конечной суммы от

Значения ε,

задаваемые

пользователем

Конечное

значение

параметра n

Значения последнего

элемента

в сумме

Значения конечной

суммы

∑

..........................................................................

1е-6

0.000000275

1.718281801

1е-7

0.000000025

1.718281826

1е-8

0.000000002

1.718281828

.............................................................................

Реализация алгоритма итерационного вычисления ряда

∑

∞

с таким

подходом может выглядеть так:

Uses Crt;

Const Eps = 1.e–7; {Задаём точность вычисления ε=0.0000001}

Var

Sum, Elm, Fact : Real; {Объявляем вещественные переменные}

n : Integer; { Объявляем переменную для вычисления n}

Begin ClrScr; {Очищаем экран процедурой ClrScr}

n := 1; {Инициализируем n}

Sum := 0; {Обнуляем переменную под значение суммы}

Elm := 1; {Инициализируем Elm для входа в цикл}

Fact := 1; {Инициализируем начальное значение факториала}

While Elm > Eps Do

Begin

Fact := Fact * n; {Моделируем значение факториала

}

Elm := 1/ Fact; { Моделируем значения элемента

}

Sum := Sum + Elm; { Моделируем сумму

∑

∞

}

n := n + 1; { Моделируем переменное значение индекса n}

End;

Writeln(‘Результат= ’, Sum); {Выводим на экран результат}

End.

Упражнения

1. Вычислить приближённое значение бесконечной суммы S с точностью

до ε=0.05. S =

1 4

4 7

3 2 3 1⋅

⋅

+ +

− +

+ 

( )( )

n n

2. Вычислить приближённое значение бесконечной суммы S с точностью

ε=0.005. S =

x x x

− + − + −

+3 5 2 1

3 5

2 1! !

( )

( )!

 

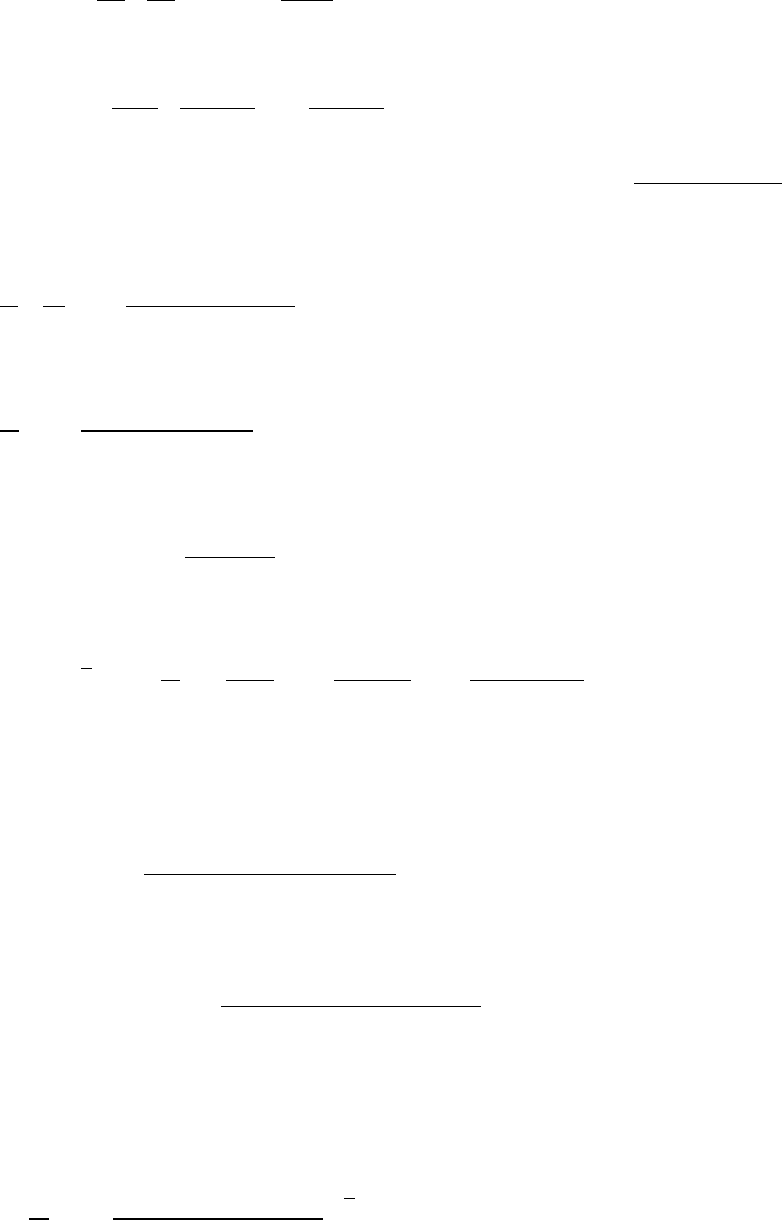
298

3. Вычислить приближённое значение бесконечной суммы S с точностью

ε=0.00001. S =

x x x

− + − + − ±

2 4 2

2 4

2! !

( )

( )!

 

4. Вычислить приближённое значение бесконечной суммы S с точностью

ε=0.00000001. S =

−

+ +

−

1 1

( ) ( )

 

5. Вычислить сумму с точностью до ε=0.00000001.

∑

∞

−+

))((

nxnx

6. Вычислить следующие суммы с определённой заранее точностью:

∑

∞

+−

=−

)14)(14(

∑

∞

+−

)12)(12(

∑

∞

−

−=

)!12(

)1(sin

( )

...

8642

11975

642

975

432

 xxxxx

⋅⋅⋅

⋅⋅

⋅

+=±

−

7. Вычислить следующие суммы с определённой точностью (при x=m, где

m–номер в журнале).

( )

∑

∞

−

−++

+=−

)1)...(1(

nmmm

( )

∑

∞

−

−++

−+=+

)1)...(1(

)1(11

nmmm

8. Вычислить ряд.

( )

∑

∞

−

−−⋅

12121

)(

299

8.21. Бесконечные произведения и их вычисления

Одним из достаточно рспространённых, является также процесс

умножения одного числа на другое. К примеру:

C := А ⋅ В;

Однако, когда количество елементов, принимающих участие в процессе

умножения, начинает возростать, вычисления такого результата усложняется.

Циклическим умножением называется процесс умножения

последовательности некоторых величин на число, отображающее результат

умножения всех ранее перемноженных чисел.

В математических выражениях оно имеет обозначение Π, а его действие

можно отобразить на графичекой схеме следующим образом (рис. 8.43).

Рассмотрим одну из формул (8.13), описывающих процесс умножения.

Если начать подставлять в неё значения n = 1, 2, 3, 4, 5, … ,

∞

, то элементы

этой последовательности сомножителей будут выглядеть так:

...

∏

∞













⋅













⋅













⋅=















(8.13)

А результаты вычисления значений этой формулы при изменениях n,

моделирующих К, приведены в таблице 8.46.

Процесс вычисления результата перемножения n елементов,

приведенный в данной таблице, ограничен величиной ε= 1е–7. Поэтому он

закончился на значении К = 3162. Следует особо отметить, что подход к выбору

проверки условия завершения вышеприведенного итерационного процесса

существенно отличается от того, который рассматривался при вычислении

формул суммирования. Это связано с тем, что значения очередного элемента

произведения влияют на конечный результат не пропорционально какой либо

постоянной величине. Поэтому в алгоритме программы вычисления

произведения был использован подход, завершающий процесс вычисления в

том случае, когда разница

между предыдущим и текущим значениями

результата умножения становится меньше ε = 1е-7 (рис. 8.44). Тогда можно

считать, что дальнейшие действия не приведут к изменению цифр значения

произведения в первых 6-ти позициях (в данном случае, при ε = 1е–7) .

=(a

× a

× … × a

k-1

)

k-1

∏

n=1

Рис. 8.42. Схема вычисления бесконечных произведений

× a