Черненко В.Д. Высшая математика в примерах и задачах (том 3)

Подождите немного. Документ загружается.

240 Гпава 26

Составим таблицу отклонений значений случайных вели-

чин от их математических ожиданий

-1,21

-0,21

0,79

-0,105

0,04

0,16

0,10

-0,05

0,15

0,05

0,15

-0,095

0,05

0,10

0,20

Дисперсии находим по формулам (2)

D(X) = (-0,105)2+(0,04+0,16+0,10)+(-0,05)2(0,15+

+0,05+0,15)+(0,095)2( 0,05+0,10+0,20)=0,0082437;

D(Y) = (-1,21)2(0,04+0,15+0,05)+(-0,21)2 (0,16+

+0,05+0,10)+(0,79)2(0,10+0,15+0,20)=0,6459.

Средние квадратические отклонения находим по формулам (3)

а, =

л/о,

0082437 = 0,09079; а^ = ^0,6459 = 0,803689.

12.2.

Закон распределения вероятностей системы двух дис-

кретных случайных величин

{X,

У)

дан в

таблице.

Найти:

а) ряды

распределения для Z и для У; б) М(Х), M(Y), D(X), D(Y),

• f^xv' 'V; в) линии регрессии У на Х и Хна У.

I^^'^"^—^

У^^--^

^•

\pi-P(x,)

0,1

0,05

0,15

0,3

0,2

0,5

0,2

0,15

0,35

^j=P(yj)\

0,6

0,4

Решение, а) Сложив вероятности по столбцам, получим

вероятности возможных значений для X, а сложив по строкам,

СПУЧАЙНАЯ ВЕПИЧИНА И ЕЕ ЧИСПОВЫЕ ХАРАКТЕРИСТИКИ 241

получим вероятности возможных значений для У.

6) М(Х) = ^]^^х,р,=\-^Л5

1-а.5 +

Ъ-0,Ъ5

1,2:

^(^^>» =

Х5=,Л^у=2-0,6+4-0,4

2,8.

D(X)

Y,(x,-M(X)fp,=

= 1,2' 0,15 + 0,2' 0.5+0,8' 0,35 = 0,46

^Г}';=ЕГ:и,-л/Г7;/^^.=о,8'о,б+1,2'о,4=о,9б

7=1

<т,

yJDfX)

л/Мб =

0.6782329

а^,

= yjD(Y) = ^096 = 0,97979.

Корреляционный момент находим

по

формуле

(9)

H:,,=t,t,(x,-M(X))(yj-M(Y))p,j=\,2-0.S-0.l

1=1 7=1

+1,21,20,05 + 0,20,80,3-0,21,20,2-

-0,80,80,2

0,81,20,15

= 0,04.

Коэффициент корреляции вычислим

по

формуле

(12)

г^=-^ = 0,06.

Находим коэффициенты регрессии

в) b(Y/X)

= г„

^ = 0,0577848, b(X/Y)

г ^

0.0276889.

• (7 <Т

"л "у

Таким образом, линия регрессии Y ни X принимает

вид:

= 0,058л:+2,67287.

242 Гпава 26

а линия регрессии Z на 7 вид:

х^т^^г^(у-т);

0,0277>;

+2,12247.

12.3.

Задана дифференциальная функция непрерывной дву-

мерной случайной величины

О прих<0 или у<0.

f(x.y) = \

Найти: М(Х

M(Y), D(X

D(Y).

Решение. Математические ожидания составляющих нахо-

дим по формулам (5). Найдем сначала дифференциальные фун-

кции:

f(^>y)

\f(^sy)dy =хе'''' ^ ye'-'dy

-хе~'';

о о ^

fi(y)^y

е~^''

^^~^^

-y е'У'.

М( X

)--^^^

х^ё""' dx

-\^ х(2хе-'' dx)--

= —('-хе +\ е dx)

А^

Jo ^ Й

Здесь, интегрируя по частям, учитывается, что интеграл

Пуассона J

е'""

dx = .

Аналогично, M(Y)

—\

у^е'^'

dy = .

Дисперсию находим по формулам (7)

л/л:

I хе ах-\

1 ( Г\ \

D(X)^-rx'e-'^'dx-\ —

=-rx'(2xe-''dx)

64 ~ 4' •'о ^ 64 4

4 Jo ^ /^4 4^ 16

СПУЧАИНАЯ ВЕЛИЧИНА И ЕЕ ЧИСПОВЫЕ ХАРАКТЕРИСТИКИ 243

Аналогично,

' ' 2^^ 64 4 16

7Г

12.4.

Внутри квадрата 0<х<—, 0<>^<— плотность рас-

пределения системы двух случайных величин f(x,y) =

= —sin(^jc +jj; вне квадрата f(x,y)=^Q.

Найти: М(Х), M(Y), D(XX D(Y), д,^, r,^,.

Решение. Математическое ожидание составляющей X на-

ходим по формуле (5)

M(X):=\''^^xf,(x)dx,

Tjxtf^(x) вычисляется по формуле ((5)

п. 10)

Гя/2 1 f 2

fx(x)

—\ sm(x

y)dx

—QOs(x-^y)\ =

Отсюда

cos

—+

JC -COSX

•

—f

sinx + cosxy.

f^/2 л:

M(^Xj =

—J

x(^mx

Л-

cosx)

dx = —.

Аналогично находим математическое ожидание составля-

ющей Y

M(Y)

[''yf(y)dy.

где

лл:/2

1 гк/2

1 ""^^ 1

= —со^(х

у)

=—(^sin

+ cos>^^;

2 о 2

244 Г пава

Г^/2 %

Г^/2

-Jo

----- • "--- 4

Дисперсии составляющих определяем

по

формулам (7)

ря/2

D(X)=r (x-M(X)/f,(x)dx

f%'f,(x)dx-[M(X)f

"^+^-2.

-\l%'A(y)dy-W(Y)t = Y^+f-2.

Корреляционный момент

по

формуле

(11)

равен

к 1

Г^^^

Г^^ ^

/t^=Mrjnr;---

-J^ J, xysin(x+y)dxdy-~

f^/2

/(-я/г

\ jc^

Jo ^r->'cos('jc+>';+sm('x+>';;|

ff/z . 7'^

«;/'—vcos/'x+v)

+ sin^x+v))

—

1 rit/l

ЛГ . . 7t^

— x(—%va.x-'rCosx—s\nx)dx

г-*»

2 16

—

((

\)xsm.x+xcQsx)ax

=—f

\)(-xco%x+

2J0

"2 16 2 2

'/^

1 T^ л:^ л: л:^

'о

2 'о 16 2 16

Коэффициент корреляции находим

по

формуле

(12)

^- ^2 16^

0.7369

_ Q,^g

"" ^D(X)^D(Y) ^^.^_2

3,0023

Глава 27

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ

СТАТИСТИКИ

27.1.

Основные понятия математической

статистики

1°,

Все объекты данной совокупности называют генераль-

ной совокупностью.

Выборочной совокупностью

(выборкой) называют совокуп-

ность случайно отобранных для обследования из генеральной

совокупности объектов.

Если случайно отобранный объект возвращается обрат-

но в генеральную совокупность, то выборка называется по-

вторной. Если же не возвращается, то выборка называется

бесповторной.

Случайная бесповторная выборка имеет место тогда, ког-

да из генеральной совокупности берется сразу нужное количе-

ство объектов.

Любой результат, вычисленный по данным выборки, имеет

погрешность, которая называется ошибкой репрезентативнос-

ти (или представительности).

246 Гпава 27

Ошибка репрезентативности характеризует величину рас-

хождения между результатами выборочного метода и соответ-

ствующими данными по генеральной совокупности.

Изменение изучаемого признака

х.

данной статистической

совокупности называется его вариацией.

Наблюдаемые значения объекта (признака) х., извлечен-

ного при выборке из генеральной совокупности, называют ва-

риантами.

Варианты принято группировать по отдельным значениям

признака (дискретная группировка) или по интервалам измене-

ния признака (интервальная группировка).

Вариационным

рядом называется последовательность ва-

риант или интервалов вариации, расположенных в возрастаю-

щем порядке.

Число наблюдений объекта

м.

при выборке называется час-

тотой. Отношение частоты к объему выборки

n-/n=W.

назы-

вается относительной частотой.

Представленная в виде таблицы совокупность вариант и

соответствующих им частот или относительных частот называ-

ется статистическим распределением выборки.

2^,

Пусть известно статистическое распределение частот

количественного (дискретного или непрерывного) признака X.

Функцией распределения

выборки или эмпирической функ-

цией распределения называется функция

F*(x),

определяющая

относительную частоту события Х<х для каждого значения х:

F*(x)

где

п^

— число вариант, при которых значение признака мень-

ше х, « — объем выборки.

Свойства эмпирической функции распределения:

функция/^*(^xj —неубьгоающая;

2) значения функции F^(x) принадлежат отрезку

[0,1];

ЭЛЕМЕНТЫ MA ТЕМА ТИ ЧЕС КОЙ СТА ТИСТИКИ 247

3) если

Ху

— наименьшая варианта, а

х^.

— наибольшая, то

эмпирическая функция

F'^(x)-

при х < х^ и

F'^{x)-\

при

х,>х^,

3°.

Геометрическая иллюстрация статистического рас-

пределения представляется графическим изображением ва-

риационных рядов: полигоном, гистограммой, кумулянтой

и огивой.

При построении полигона частот на оси абсцисс прямо-

угольной системы координат откладывают варианты х., а на

оси ординат — соответствуюш^ие им частоты

п^.

Ломаная линия,

соединяющая точки

(х^.,г?.),

называется

полигоном

частот,

^zm^

по оси ординат откладывать относительные частоты vv. — соот-

ветствующие вариантам

х^,

то ломаная

линия,

соединяющая точ-

ки (x^,w^.), называется полигоном относительных частот.

Гистограмма— графическое изображение интервального

вариационного ряда.

случае непрерывного распределения при-

знака в некотором интервале, интервал разбивают на несколько

частичных интервалов длины

и находят суммы частот

п.

в каж-

дом частичном интервале. При построении гистограммы на оси

абсцисс откладывают интервалы значений признака

Л,

и на каж-

дом из них, как на основании, строят прямоугольник с высотой

равной отношению

«^./Л,

где

п^

— частота вариант /-го интерва-

ла; «.

— плотность частоты. Площадь гистограммы частот

равна сумме всех частот, т. е. объему выборки.

Если высоты прямоугольников равны w./h —плотности

относительных частот, то ступенчатая фигура, состоящая из этих

прямоугольников, называется

гистограммой относительных

ча-

стот.

Накопленной частотой в точке х. называется суммарная

частота элементов статистической совокупности со значениями

признака, меньшими чем х^.

Кумулятивным рядом называется ряд накопленных частот

{х), члены которого соответствуют границам интервалов или

значениям признака.

248

Гпава 27

Если

на

оси

ординат откладывать накопленные частоты у, (^)

а на

оси

абсцисс соответствуюище границы интервалов

х^,

то

лома-

ная

линия,

соединяющая точки л:., 7, (^)

называется кумулянтой.

Если на оси абсцисс откладывать накопленные

частоты,

а на

оси ординат границы интервалов

или

значение признака, то лома-

ная

линия,

соединяющая точки (у^ (х),

х^),

называется огивой.

1.1. Выборка задана в виде распределения частот

-\-

Написать распределение относительных частот. Построить:

а) полигон частот; б) полигон относительных частот; в) найти

эмпирическую функцию

построить ее график.

Решение. Найдем объем выборки

^=1+3+7+5+4 = 20.

Деля частоты на объем выборки, находим относительные

частоты

^1=ТГ = 0,05; м;2=:^ = 0,15; >Уз=^ = 0,35;

20 20 20

w,= —= 0,25;

W5=

—= 0,2.

'20 '20

Распределение относительных частот примет вид

1 ^,-

0,05

0,15

0,35

0Д5

ОД

Проверка

2^^^jW,.

=0,05 + 0,15 + 0,35 + 0,25 + 0,2 =

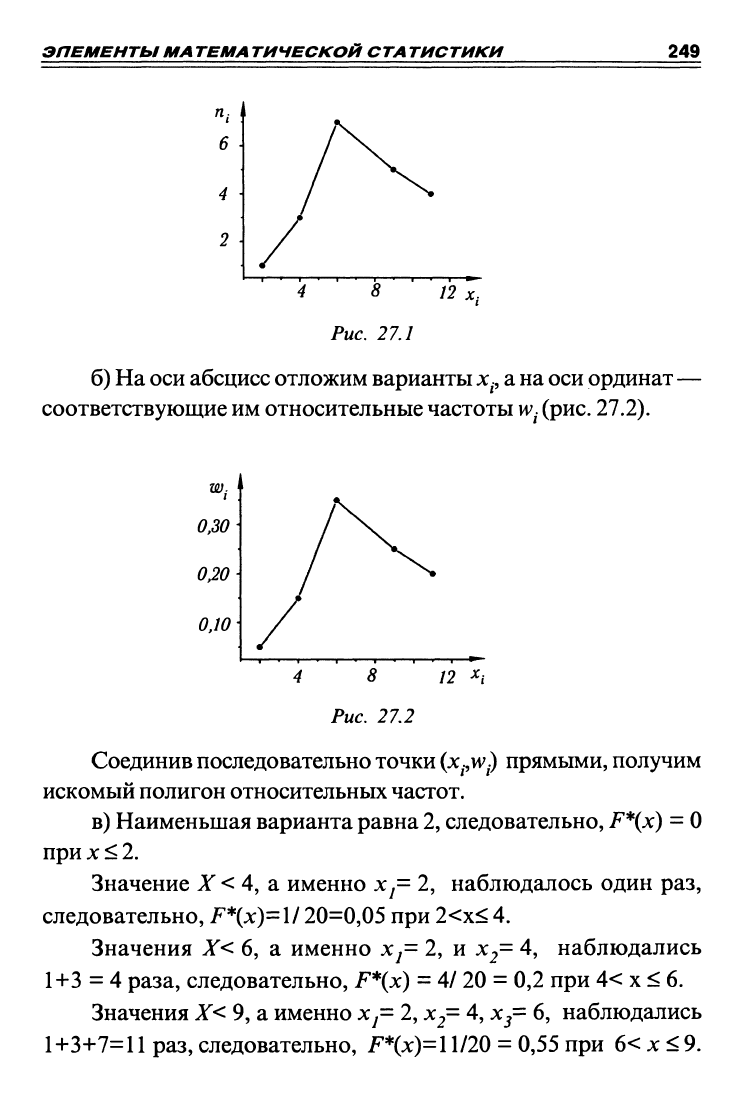
а) На оси абсцисс отложим варианты

х^,

а на оси ординат—

соответствующие частоты

п^

(рис. 27.1).

Соединив последовательно точки

(х^.,«^)

прямыми, получим

искомый полигон частот.

ЭПЕМЕНТЫ MA ТЕМА ТИЧЕСКОИ СТА ТИСТИКИ

249

б)

На

оси

абсцисс отложим варианты

л:.,

а на оси

ординат -

соответствующие

им

относительные частоты

(рис.

27.2).

12 ^i

Соединив последовательно

точки {x.,w)

прямыми, получим

искомый полигон относительных частот.

в) Наименьшая варианта равна

следовательно, F\x) =

при

х<2.

Значение Z

4, а именно Ху= 2, наблюдалось один раз,

следовательно, F\x)-\l 20=0,05 при 2<х< 4.

Значения Х< 6, а именно Ху= 2, и ^2= 4, наблюдались

1+3 = 4 раза, следовательно, F\x) = 4/ 20 = 0,2 при 4< х < 6.

Значения Х< 9, а именно х^-

^2= 4, х^= 6, наблюдались

1+3+7=11 раз, следовательно,

F*(x)=l

1/20 = 0,55 при 6< х