Черненко В.Д. Высшая математика в примерах и задачах (том 3)
Подождите немного. Документ загружается.


W Глава 21
Для
того,
чтобы найти формулы связи одного и того же век-
тора г
в
двух взаимных системах, умножим скалярно все члены
равенства х.е'
=
х'е. на основные векторы каждой системы,
тогда получим ^
^' = ё^Ч-; ^i^eij^'- (6)
Из (5), (6) следует, что координатные векторы определя-
ются через векторы взаимной системы, как координаты взаим-
ной системы. Таким образом, координаты и базисные векторы,
принадлежащие одному
и
тому же координатному триэдру, пре-
образуются как базисные векторы и координаты взаимной сис-
темы.
3°.
Рассмотрим соотношения между двумя независимыми
прямолинейными координатными системами. Индексы
у
второй
системы координат отметим штрихами. Пусть начала этих сис-
тем совпадают. Введем следующие обозначения
e.'e^'=g!;
e'-e.^=gi,
причем g,f=gfi; /=g^\-
gi^^f^
Повторяя вывод, аналогичный выводу зависимостей (5),
получим
ei=giie^=gire^'=g!ej^;
e'=g'-ej=g}'e^'=g'^'e.;
er=gn''e''=gjre'=gre,; (7)
Для радиус-вектора имеем
г = х'
•
в,.
=
X;
•
ё^
=
х-^
•
ё' =
х^
•
ёг.

ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСПЕНИЯ
11
Скалярно умножая все части этих зависимостей на масш-
табные векторы любой из рассматриваемых координатных сис-
тем, получим
x'=g'-x^=g'rx>^g"-x.;
h=eii-x'=g'-x.=g,.-x>;
х'
=
g'''•
X,.
=
g[
•
х'= g'''•
X,;
Xi'=gir-x'=g}-x,=gjrx'.
(8)
Так как векторы основной координатной системы приня-
то обозначать нижними индексами, то одинакого изменяющи-
еся с ними координаты, а также координаты любых векторов
и сами векторы, имеющие в обозначениях также нижние ин-
дексы, называются ковариантными. Векторы взаимной и ко-
ординаты основной системы, соответственно, называются
контравариантными, т. е. У — контравариантные коорди-
наты некоторого вектора, если выполняется условие
x'-g'-x^.
в случае прямолинейных ортогональных координат необ-
ходимость в верхних индексах отпадает и все индексы ставятся
внизу.
1.1. Возьмем шесть векторов
a,b,c,p,qj
и докажем следу-
ющее тождество
[а-(бх?)][р.(^хг)]:
а-р Ь'р С'р
aq bq c-q
a-r b-r С'Г
Решение. Если представить смешанные произведения через
составляющие векторов, то равенство сводится
к
умножению оп-
ределителей 3-го порядка
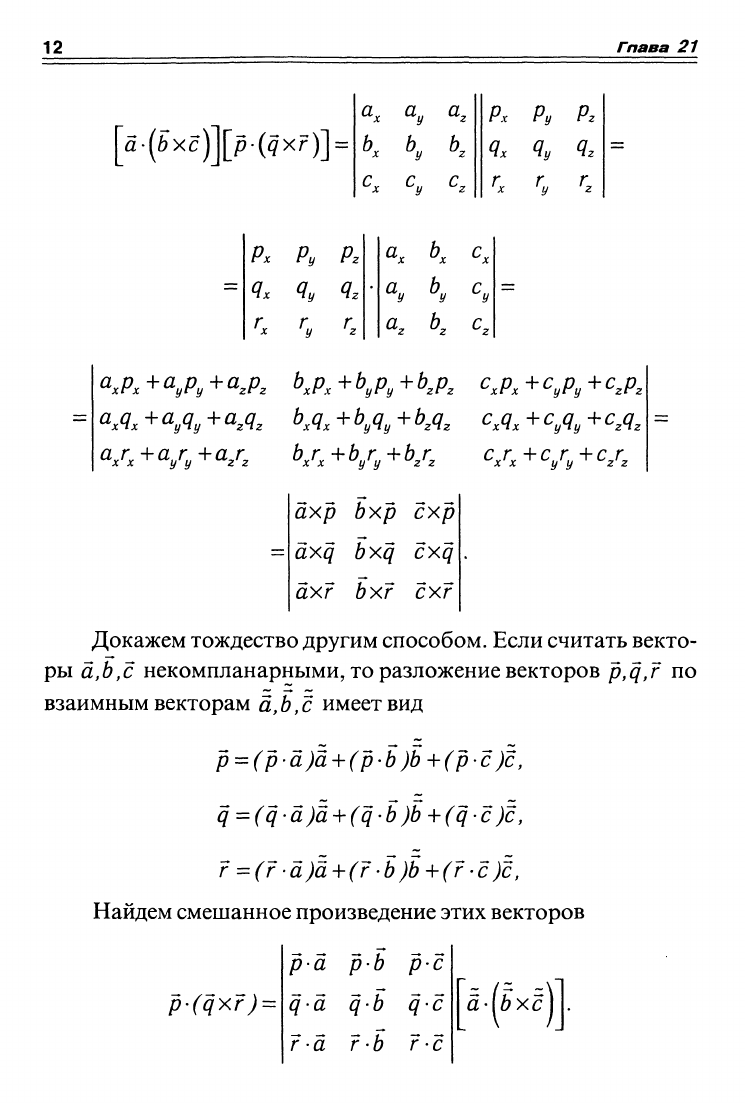
12
г пава 21
[а(бхс)][р(^хг)] =
а а а
X
у Z
к
К К
С С С
X у ^z
Р.
Ру Рг
Ях
Яу Яг
Гг
Р.
Я.
Г
Ру
Рг
Чу Чг
'у 'г
а, К с.
ау 6, с^
а, Ь, с.
а.Ях
+
a^qy
+ a^q,
b^q,
+
b^q^
+
b,q^
c^q^
+
c^q^
+ c^q^
a r +a r +a r
'^x X у у г г
ЬЛ+Ь/у-^Ь/г
^хГ.+^,+СЛ
ахр Ьхр схр
axq bxq cxq
axr bxr cxr
Докажем тождество другим способом. Если считать векто-
ры а,Ь,с некомпланарными, то разложение векторов p,qj по
взаимным векторам а,
В,
с
имеет вид
р
=
(р- а)а + (р
• b )Ь
+ (р' с)с,
q =(q- d)d + (q
• b
)b
+
(q 'C)c,
r =(r -dja-^fr-b)b -h(r
•
c)c,
Найдем смешанное произведение этих векторов
\p-d p-b р'С
p-(qxf)
=
\q'd qb q-c
f-d
f'b r-c
d-lbxc)
.

ЭПЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСПЕНИЯ 13
Пользуясь зависимостями
(1),
(2), получим
•(бХС) = =: ,
V /
а-ГЬхс)
откуда
[а-(^х?)][р.(^хг)] =
(Ьхс)
а-р Ь'р С'р
d-q bq c-q
d'f b-r C'f
21.2.
Определение ортогонального
тензора второго ранга
1"^.
Рассмотрим две прямолинейные прямоугольные систе-
мы координат х^,Х2,х^ и х[,х\,х^ с координатным базисом
вр
^2,
^3
и
е\,
ё[,
вз
соответственно. Формулы связи между базис-
ными векторами (7,
п. 1)
примут вид
^/=ад;
^/=eff^
Г^-,/
=
1,2,ЗЛ
где gii — косинусы углов, составляемых осями этих координат-
ных систем.
Проекции радиуса вектора на оси одной системы коорди-
нат, выраженные через проекции в другой системе координат
(8,
п.
1),
будут
h^ei/r
^j=Sij^i' (1)
Совокупность трех скалярных величин х., преобразующих-
ся по формулам (1) в величины Ху, определяют ортогональный
вектор, который является инвариантом, поскольку
не
зависит от
системы координат.

14
Гпава 21
Обобщая предыдущие соображения на вектор, приведем
определение ортогонального тензора второго ранга.
Совокупность трех векторов р., заданных в одной системе
координат X. и преобразующихся по формулам
Pi=gijPr' Pi=SijPi (2)
в векторы
p'j,
отвечающие другой системе координат x'j, опреде-
ляют
ортогональный тензор
второго ранга или просто тензор.
2^.
По аналогии с вектором введем для тензора обозначе-
ние
7 = ejpj+e2P2+e3p3. (3)
Поскольку тензор определяется тремя векторами
p^^Pi^P^'
то разложение этих векторов по координатному базису имеет вид
А ==Рп^1+Р12^2+Аз^з/
Р2=Р2Д-+-Р22^2+Р23^3/ И)
Рз=РзД+Рз2^2+Рзз^З-
Числа
pij
называются
компонентами тензора
и могут быть
записаны в виде матрицы, определяющей тензор
7 =
Ри
Р21
Р31
Рп
Рп
Р32
Pl3
Р23
Рзз
(5)
У. Подставляя (4) в (3), получим диадное представление
тензора
Т =
р,,ё,ё,
+Р,2?,?2 +Pl3^I^3 +Р21^2^1 +
'^Pii^i^i +Р2з^2^з "^Рз1^з^1
^
Ръг^ъ^г
^
Ръъ^ъ^ъ
"^
Pij^i^j-
(6)
Выражения
ё^ё.,
представляющие собой определенную пос-
ледовательную запись двух взаимно независимых векторов без

ЭПЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСПЕНИЯ
15
каких либо знаков умножения, называются
диадами,
а умноже-
ние,
соответственно, диадным.
4°.
Если для любой системы координат компоненты тензо-
ра равны Рц =
Р22
-
Ръъ
-
Ь Рц
=^0(1^
j) , то тензор называется
единичным и обозначается
/ =
1
О О
О
1 О
О
О 1
} = е^е^ +^2^2
+^3^3-
(7)
Если
у
тензора значения компонент
не
меняются от переста-
новки индексов
Pij
= pji, то он называется
симметричным
тен-
зором .
Тензор 7^, у которого переставлены векторы в диадах или
транспонирована матрица, называется тензором,
сопряж:енньш
с тензором f.
(8)
Нетрудно заметить, что симметричный тензор является со-
пряженным самому себе, т. е. f^-f,
Если у тензора значения компонент при перестановке ин-
дексов меняются на противоположные
Ду
=""Ру7
(0~Ь2,3), то
тензор называется антисимметричным. Компоненты антисим-
метричного тензора, расположенные на главной диагонали,
равны нулю, т.к. д^ = -р..
т.
А
Ри
Рп
Аз
Ргх
Ри
Ри
Р31
Р32
Рзз
гдей>, =Рз2 =
Тл=^
-Рп> Щ
0 -щ
щ 0
-й)2 Щ
= Р\Ъ=-Ръ\'
«2
0
й)з =
Рп
(9)
= -pl2-

16
гпава 21
Отсюда видно, что тензор, сопряженный антисимметрич-
ному, отличается от него только знаком. Любой тензор можно
представить в виде
с^ммы
симметричного и антисимметрично-
го тензора
Рц = ^ц
+ S- =
2^Pii
+
Pji)
^-^(Pii -
Pji
)'
(10)
2,1.
Разложить на симметричную и антисимметричную ча-
сти диаду аЬ . Выяснить значение аксиального вектора, соот-
ветствующего антисимметричной части.
Решение. По формуле (10) тензор представляется в виде
суммы симметричного и антисимметричного тензора. Посколь-
ку тензор задан в диадном виде, то симметричная часть равна
5ц =
-(Рц
+ Рц
)
=
-(аЬ
+
Ьа) -
а,Ь,
-(ар^+афО
-(ар^+аф^) -(a,b,+a,bj
аф^
1
-(аф^
+ аф^)
-(аф,
+
аф^)
(аф,+аф^
аф.
Антисимметричная часть с учетом формулы (9) будет
^ч=1^(Рч-рц) = ^(^^-'^а) = { Щ О -«,
О -ft).
ft).
-О),
(У,
о
где величины
ft),,
о^, щ можно рассматривать как компоненты
некоторого аксиального вектора S), то есть ш =
co^i + (Ojj
+ (оф.
Учитывая, что щ=р^2' ^i-Pw ^i~p2i> запишем аксиаль-
ный вектор
в
диадном виде

ЭПЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСПЕНИЯ 17
или
^
=
т[(^3^2-^2)^
+
(^А-^Л)7
+
М1-М1)^]
Ш
=
/
й,
«1
/
Ьг
Cj
yfe
^3
(h
1
-
=—bxd.
2
21.3.
Операции над тензорами
1^.
Сумма двух тензоров
с
компонентами
р^у и р-
равна
тензору, компоненты которого равны сумме одноименных ком-
понент складываемых тензоров
Pij=Pij+Pir-
(1)
2°.
Если все компоненты р^у некоторого тензора умножить
на скаляр Я,
то
получится новый тензор
с
компонентами
^pij.
Скалярное произведение тензора
f на
вектор
а
дает век-
тор
b
. Если тензор задан в диадном виде
(6,
п.21.2),
то
произве-
дение тензора
на
вектор
а
=
а.е^
справа равно
+е,(р,,а, + рз.а^ +
р^^а^) =
p,ja.e,
= Ь,ё,,
(2)
где
Ь-
= р.
а. —компоненты вектора
Ь
•
Следует отметить,
что при
скалярном умножении вектора
на диаду скалярно перемножаются соседние векторы.
При скалярном умножении тензора
f на
вектор
а =
а.е.
слева получим вектор
с
аТ
=
аё-
•
р.её- =ар е =с е-,
где с
J =
a.p.j
— компоненты вектора
с

18
Г пава 21
Таким образом, скалярное произведение тензора на вектор
справа и слева не равны друг другу а-Т ^f -а.
Пусть вектор b в правой части выражения (2) коллинеарен
вектору а, т. е. b =Ха. Величина Я называется главным (или
собственным) значением тензора. В этом случае равенство (2)
будет
Т-а-Ха
или в развернутом виде
р„а,+р,2^+р,з^=Яа^;
Рз1^1+Рз2^2+Рзз^з='^
из-
данная система однородных уравнений имеет решение от-
личное от нуля, если ее определитель равен нулю
Рц-^
Рм Рхъ I
Р2\
РЦ-^ Р23 =0- (3)
Р31 Р32 РзЗ-^|
Запишем кубическое уравнение (3) в виде
Я'-/,ЯЧ/2Я-/з=0,
где /р /2, /з — главные инварианты, равные
А =Р11+Р22+РЗЗ'*
Л =
Р22
Ргз
Ръг
Ръъ
4-
Рп Рз1
Аз Рзз
4-
Рп Pi\
Рп Ргг
Ри
Рп Рп
Ргх
Ргг Рп
Ръх
Рз2 Ръг

ЭПЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСПЕНИЯ 191
Тензоры, у которых первый инвариант равен нулю /j = О,
называются девиаторами.
У. Векторное произведение тензора f на вектор а справа
равно тензору, который обозначается Тха
+р,,ё,(ё,ха)
=
p..e.(ejXd),
Аналогично, векторное произведение тензора f на вектор
а слева равно
ахТ
=
р..(ахё.)ё.. (5)
4°.
Скалярное произведение тензора
Л
=
а^п^.е^
на тензор
В =
b^je^ej
равно тензору f равному
Т
=
А'В
=
а-Х-ё,(ё^
•
ё^)ё^
=
a.XjS^Jfi.
=
(6)
3
где p,j
=
a.,b,j
+
a.^b^j
+
a.^b^j
=
^ a.^^ (i, j
=
1,2,3;,
т. е. опреде-
/1=1
литель произведения двух тензоров равен произведению опреде-
лителей этих тензоров.
Скалярное произведение тензоров обладает свойствами ди-
стрибутивности и ассоциативности
М,+Л2;Б
=
ДБ4-Л2-В,
(тА)'В
=
т(А'В),
(АВ)'С
=
А(В'С)
=
А'ВС.
