Черненко В.Д. Высшая математика в примерах и задачах (том 3)

Подождите немного. Документ загружается.

270 Гпава 27

Разрешая относительно

(9),

(10)

при определении доли при-

знака, для повторной выборки получим

п= ^, Л (13)

для бесповторной

= -

Nt^pq

5.1.

Найти доверительный интервал для оценки мате-

матического ожидания нормально распределенной величины

с надежностью 0,95, если известно генеральное среднее квад-

ратическое отклонение а =4, объем выборки п=36 и выбо-

рочная средняя jc=8.

Решение.

Для

нахождения доверительного интервала восполь-

зуемся формулой (1). Значение t находим из соотношения

Ф(() =

—

0,475

по таблице

(3):

t-1,96. Подставив все значения

в формулу

(1),

получим

8-1,96-Д-<а<8

1,96 ^

136 л/36

6,794<а<9,206.

5.2.

Известно

среднее квадратическое отклонение (J = 3 нор-

мально распределенной генеральной совокупности. Найти с на-

дежностью

0,95:

а) минимальный объем выборки, если точность

оценки математического ожидания генеральной совокупности по

выборочной средней равна

<5=

0,2; б) точность 5, с которой вы-

борочная средняя оценивает математическое ожидание, если вы-

борка объема п= 100.

Решение, а) Для определения минимального объема выборки

воспользуемся формулой (2) п = . По условию /=0,95, тог-

ЭЛЕМЕНТЫ MA ТЕМА ТИЧЕСКОЙ СТА ТИСТИКИ

271

да Ф(0=0,475 и по таблице

(3)

находим t = 1,96. Искомый объем

2 ^2

выборки п =

1^96М

ГО,

я =

1,96-3

t 0,2

= 869.

б)

Для определения точности оценки математического ожи-

дания генеральной совокупности по выборочной средней вос-

пользуемся формулой (2). Поскольку при 7 = 0,95 значения

t =1,96, то точность оценки выборки объема и = 100 равна

5 = 1,96

лЛоо

= 0,588.

5.3.

Из генеральной совокупности извлечена выборка

",•

Оценить с надежность 0,99 математическое ожидание нор-

мально распределенного признака генеральной совокупности по

выборочной средней.

Решение. Математическое ожидание будем оценивать при

помощи доверительного интервала. Поскольку среднее квадра-

тическое отклонение генеральной совокупности неизвестно, то

для оценки математического ожидания воспользуемся формулой

(3).

Выборочную среднюю находим по формуле

х=5^«.х> = ^2-2 + 3-3 + 6-5 +

4-8;/15

= 5.

Исправленное среднее квадратическое отклонение находим

по формуле

44f8-5/;/14/'=2,1679.

Пользуясь таблицей

(4)

по у- 0,99

и /?

находим / = 2,98.

272 Гпава 27

Подставляя найденные величины в формулу (3), получим

искомый доверительный интервал

^ ^^^2,1679 ^ ^^^2,1679

5-2,98

г— <fl<5 +

2,98—j=r~;

Vl5 Vl5

3,3319

<a< 6,6681.

5.4. По данным 7 независимых испытаний физической ве-

личины найдено среднее арифметическое результатов отдельных

измерений J = 50,7 и исправленное среднее квадратическое от-

клонение

4,5.

Оценить истинное значение измеряемой вели-

чины с надежностью у- 0,99.

Решение. Истинное значение измеряемой величины равно

ее

математическому

ожиданию.

Следовательно, решение сводит-

ся к оценке математического ожидания при неизвестном сред-

нем квадратическом отклонении генеральной

совокупности.

Рас-

сматривая число измерений, как объем выборки, математичес-

кое ожидание (истинное значение измеряемой величины) оценим

при помощи доверительного интервала по формуле

(3).

Значе-

ние

определяем по таблице (4) при / = 0,99 и п = 7: / = 3,71.

Подставляя все величины в формулу (3), получим

50,7-3,71^< л < 50,7 +

3,71^;

л/7 л/7

44,389<а<57,01.

5.5.

По выборке объема

из генеральной совокупнос-

ти найдено исправленное среднее квадратическое отклонение

5 = 1,2 нормально распределенного количественного признака

X, Найти доверительный интервал, покрывающий генеральное

среднее квадратическое отклонение а с надежностью 0,95.

Решение. Доверительный интервал в данном случае нахо-

дится по формуле (4) или (5) в зависимости от q. Так как при

ЭПЕМЕНТЫ MA ТЕМА ТИ ЧЕСКОЙ СТА ТИС ТИКИ

273

у = 0,95 и « = 12 по таблице (5) q = 0,55 < 1, то искомый дове-

рительный интервал находим по формуле (4)

1,2П-0,55;<С7<1,2П

+ 0,55;;

0,54 <(Т< 1,86.

5.6. Найти точность прибора

надежностью 0,99, если по 8

равноточным измерениям некоторой величины найдено, что ис-

правленное среднее квадратическое отклонение равно

= 0,25.

Решение. Точность прибора определяется средним квадра-

тическим отклонением

случайных ошибок

измерений.

Найдем

доверительный интервал, покрывающий

<т с

заданной надежно-

стью у= 0,99. Поскольку при /= 0,99 nn = Suo таблице (5) зна-

чение ^

1,38>

то воспользуемся неравенством (5)

0<сг<0,25П +

1,38;;

< а < 0,595.

5.7. Результаты урожайности риса на различных участках

поля площадью 1000 га приведены в следующей таблице

урожайность

в ц.

с га

количество га

10-12

12-14

14-16

16-18

Найти:

а) при

повторной

бесповторной выборке вероятность

того,

что средняя урожайность риса на всем поле отличается от

средней выборочной

не

более чем на

0,1

ц; б) границы,

которых

с вероятностью

0,9973

заключена урожайность на всем поле.

Решение, а) Принимая за значение признака середины ин-

тервалов, найдем среднюю арифметическую

дисперсию задан-

ного в условии распределения

_ Уп.х,

15-11

+ 20'13 + 45'15 + 20-17 ,^^

- - "^ = = 14,4;

+ 20

X =

274

Гпава

тг \2

'^щ(х,-х)

15(^-3,5/

+20Г-1,5/ +45(^0,5/ +20f

2,5/

= 2,53.

При определении вероятности искомого события восполь-

зуемся формулой

(6),

в которой 5 =

0,1.

Найдем среднюю квад-

ратическую ошибку выборки jJ.. Для повторной выборки по

формуле

(7),

в которой п=

100,

получим

2,53

'юо

= 0,16.

Искомая вероятность по таблице

Р(\Х-14А\<0,\)

= 2Ф

^0,1 ^

1,0,16

= 2Ф(0,625) = 0,468.

случае бесповторной выборки по формуле

(8),

(6) и табл.

(3) имеем

2,53

100

РЛХ-14,4 <

0,1;

= 2Ф

1000

0,1

= 0,150897.

= 2ФГ0,6627; = 0,49.

0,151

б) По таблице (3) и правилу трех сигм

Pf|X-3c|< 5; =

20(^3;

0,9973

находим, что д = Зц.

Если выборка повторная, то 5 =30,16=0,48 ц; если беспов-

торная, то 5 = 30,150897=

0,45269

ц.

Таким образом, средняя урожайность при повторной вы-

борке на всем поле

вероятностью

0,9973

находится по форму-

ле (3) и заключена в границах

ЭПЕМЕНТЫ MA ТЕМА ТИЧЕСКОЙ СТА ТИСТИКИ 275

х-5<Х<х+5; 14,4-~0,48<Х <

14,4

+ 0,48;

13,92 <Х< 14,88;

если выборка бесповторная

14,4-0,45

<^<14,4

+ 0,45;

13,95 <^< 14,85.

5.8.

партии из 10000 лампочек было проверено

1000

лам-

почек. Среди проверенных оказалось

бракованных. Найти:

а) при повторной

бесповторной выборке вероятность того, что

доля бракованных лампочек во всей партии отличается от их

доли в выборке не более чем на 0,01. б) границы, в которых с

вероятностью

0,9836

заключена доля бракованных лампочек во

всей партии.

Решение, а) Средняя квадратическая ошибка при повтор-

ной выборке при доле бракованных лампочек в выборке w=0,05

по формуле (9) равна

0,05-0,95^

V 1000

при бесповторной выборке

объеме генеральной совокупности

Л^= 10000 равна

_ 0,05 0,95 Л 1000

1000 10000

= 0,0065364.

Искомая вероятность при повторной выборке будет

^ 0,01 "»

Р(\р-0Щ<0М) =

2Ф

при бесповторной

0,00689

= 0,853,

Р('|/?-0,05|<0,01;

= 2Ф

^ 0,01 "1

0,006536;

= 0,874.

276 Гпава 27

б) По таблице (3) находим, что Ф(2,4) = 0,9836; откуда

, = i = 2,4.

Средняя квадратическая ошибка, если выборка повтор-

ная,

/I = 0,00689, а, если выборка бесповторная, \i = 0,0065364.

Таким образом, предельная ошибка для повторной выборки

д =

2,40,00689

= 0,0165;длябеспоеторной5 =

2,4-

0,0065364=

0,0157.

Границы, в которых

вероятностью

0,9836

заключена доля

бракованных лампочек, для повторной выборки равна

0,5-0,0165

<Р< 0,5 + 0,0165;

0,4835

<Р< 0,5165,

для бесповторной

0,5-0,0157

<Р<0,5 + 0,0157;

0,4843

<Р< 0,5157.

5.9. При каком объеме повторной выборки можно утверж-

дать с вероятностью 0,9836, что отклонение выборочной сред-

ней от генеральной не превысит 8 = 0,2, если а = 0,9?

Решение. Из выражения (6) имеем

Р(^|Х-Зс|< 0,2; = 20(^0 = 0,9836,

откуда по таблице (3) t = 2,4. Поскольку выборка повторная,

то полагая сг-^^ по формуле (11) ее объем равен

2,4^ 0,9^ м^

П= :; = 117.

0,2'

5.10. Из партии в

1000

деталей для определения доли брака

производится выборка. Найти объем выборки, при котором с

вероятностью Р

0,9973

гарантируется ошибка не свыше 0,2,

если: а) выборка повторная; б) выборка бесповторная и вероят-

ность изготовления бракованных деталей равна q = 0,2.

ЭПЕМЕНТЫ MA ТЕМА ТИЧЕСКОЙ СТА ТИСТИКИ

Т11

Решение.

условии

нет

значения доли брака, поэтому при

определении объема выборки в формуле (13)

следует

использовать наибольшее

значение/?^

= 0,25.

Таким образом,

учитывая,

что при

заданной вероятности по

формуле

(6)

/ =

получим п = —

57.

и,

б) По условию P(\w-p\

0,2) =

0,9973

значение t - 3,

= 1- ^ = 0,8. Величина выборки по формуле

(14)

равна

1000-90,8а2

п =-

= 34,749.

10000,2Ч90,8а2

5.11.

При изучении физико-механических свойств ткани

было испытано

=12 образцов и получены следующие значе-

ния предела прочности на разрыв

Н1мм^:

19,5;16,8;17,1;17,5;

15,7;

15,5; 14,6; 20,0; 19,4; 18,2; 16,2; 19,2. Требуется: а) найти

выборочное среднее х , «исправленное» стандартное откло-

нение s(x) и коэффициент вариации v изучаемого признака;

б) найти доверительный интервал для среднего предела проч-

ности

этой ткани на уровне заданной надежности

= 0,95.

Решение, а) Вычисления будем вести

табличном

виде.

За-

пишем результаты наблюдений в столбец

таблицы и найдем

их сумму

пределы прочности

19.5

16.8

17.1

17.5

15.7

15.5

(х^-х)

2.02

-0.68

-0.38

0.02

-1.78

-1.98

fx,-j/

4.08

0.46

0.14

0.00О4

3.17

3.92

278

Гпава

14.6

20.0

19.4

18.2

16.2

19.2

I 209.7

-2.88

2.52

1.92

0.72

-1.28

1.72

8.28

6.35

3.69

0.52

1.64

2.96

135.21

Выборочное среднее равно

х= i = -l-У;c.=^^^ = 17,48Я/лш^

„У" X, 12tr ' 12

Вычислим отклонения (х. -J) и внесем их в столбец 2. В

столбец 3 запишем квадраты (х. - х/ этих отклонений и най-

дем их сумму

2^(x.-xf

=35,21.

Найдем «исправленное» стандартное отклонение

Коэффициент вариации v изучаемого признака

,. s(x) ,_/ 1,79

% =

•

100%

= 10,24%.

X 17,48

б)

Для заданной доверительной вероятности у

0,95 и чис-

ла степеней свободы V=AI-1=12-1=11H3 табл.4 находим

t^(0,95;

11^-2,20. В случае малой выборки п < 30 предельная

ошибка выборки определяется по формуле

/^^у,у;^ =

2,2-^2

:=.lД4Я/мм^

yjn vl2

Искомый

95%

-ный доверительный интервал для ожидаемого

предела прочности а исследуемой ткани определяется неравен-

ЭЛЕМЕНТЫ MA ТЕМА ТИЧЕСКОИ СТА ТИСТИКИ

279

СТВОМ х-А<а<х4-А, откуда 17,48-1Д4< (Я<17,48+1,14 или

16,34<

а<

18,62.

Таким образом, средний предел прочности тка-

ни находится

интервале от 16,34

Н1мм^

до 18,62 Н/мм^.

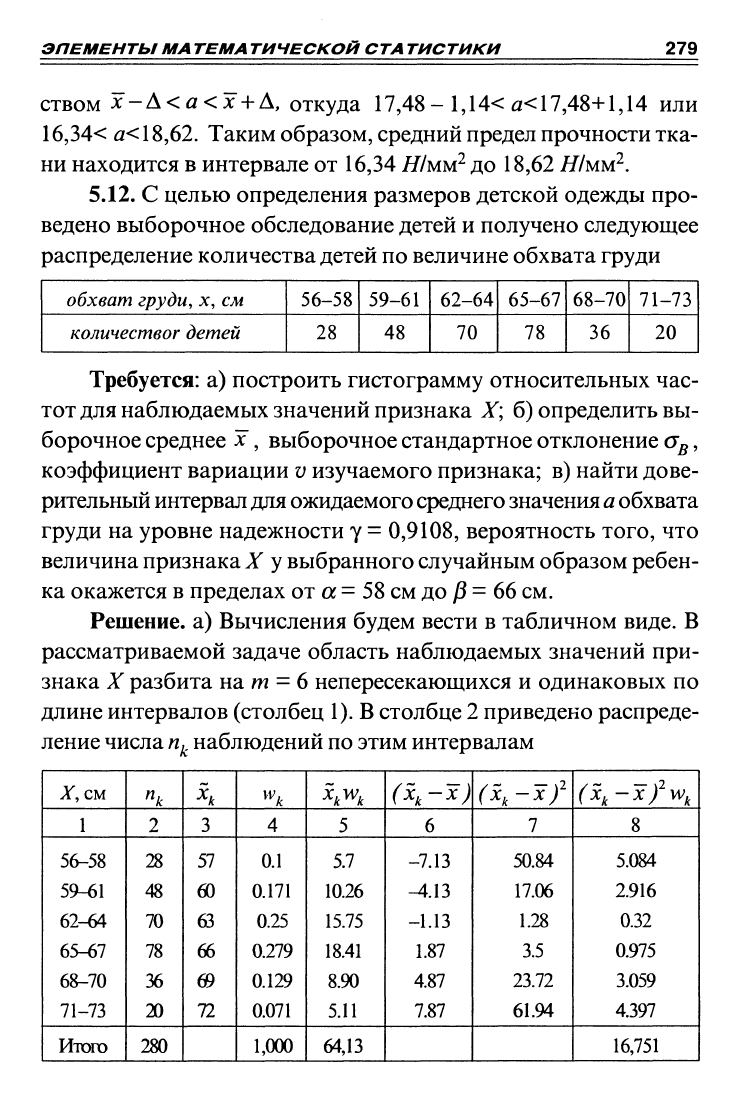
5.12. С целью определения размеров детской одежды про-

ведено выборочное обследование детей и получено следующее

распределение количества детей по величине обхвата груди

обхват груди, х, см

количествог детей

56-58

59-61

62-64

65-67

68-70

71-73

Требуется: а) построить гистограмму относительных час-

тот для наблюдаемых значений признака Х\ б) определить вы-

борочное среднее х , выборочное стандартное отклонение а^,

коэффициент вариации v изучаемого признака; в) найти дове-

рительный интервал для ожидаемого среднего значения

обхвата

груди на уровне надежности у = 0,9108, вероятность того, что

величина признака X у выбранного случайным образом ребен-

ка окажется в пределах от

а:

= 58 см до

= 66 см.

Решение, а) Вычисления будем вести в табличном виде. В

рассматриваемой задаче область наблюдаемых значений при-

знака X разбита на w = 6 непересекающихся и одинаковых по

длине интервалов (столбец 1). В столбце 2 приведено распреде-

ление числа

Uj^

наблюдений по этим интервалам

Х,си

56-58

5^-61

62-64

63-67

68-70

71-73

Итого

"к

280

'Ч

0.1

0.171

0.25

0.279

0.129

0.071

1,000

ХкЧ

5.7

10.26

15.75

18.41

8.90

5.11

64,13

(х^-х)

-7.13

^.13

-1.13

1.87

4.87

7.87

(x,-xf

50.84

17.06

1.28

3.5

23.72

61.94

(x,-x)'w,\

5.084

2.916

0.32

0.975

3.059

4.397

16,751