Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент
Подождите немного. Документ загружается.

81
поскольку операция А должна быть завершена ко второму дню, она не может начаться позже, чем
в исходный день, следовательно, значение LS для этой операции равно 0.
d) Наконец определяется резерв времени для каждой операции. Он определяется либо разницей
LS - ES, либо LF - EF. В рассматриваемом нами примере резерв времени существует только для
операции С (один день), следовательно, критический путь проходит через операции А, В и D.
Графики раннего и позднего начала операций
Графиком раннего начала операций (Early Start Schedule) называется график, в котором все
операции проекта приведены по ранним срокам от начала реализации проекта. Если операция
расположена вне критического пути, то между моментом ее завершения и началом следующей
операции будет резерв времени. Когда проект выполняется по такому графику, он и все
составляющие его операции будут завершены в максимально короткие сроки.
В графиках позднего начала операций (Late Start Schedule) все операции приведены по
наиболее позднему сроку, в который их можно начать, не задерживая при этом даты завершения
всего проекта. С помощью такого графика можно определить максимально возможную задержку
моментов приобретения материалов, использования рабочей силы, осуществления других затрат и
применить ее для эффективного использования соответствующих ресурсов.
Сетевой график разработка новой модели компьютера
Выполнив все описанные выше процедуры для примера 3.1, мы определили критический путь и
поздние и ранние сроки начала операций для проекта создания новой модели компьютера.
Полученные результаты приведены на рис. 3.4.
Обратите внимание, что в данном случае мы получили сетевой график, в котором два
критических пути. Первый проходит через операции А, С, F, D и G, а второй — через А, В, D, F и
G. Следовательно, вне критического пути находится только одна операция Е. Это означает, что
реализовать данный проект в минимальные сроки будет довольно сложно.
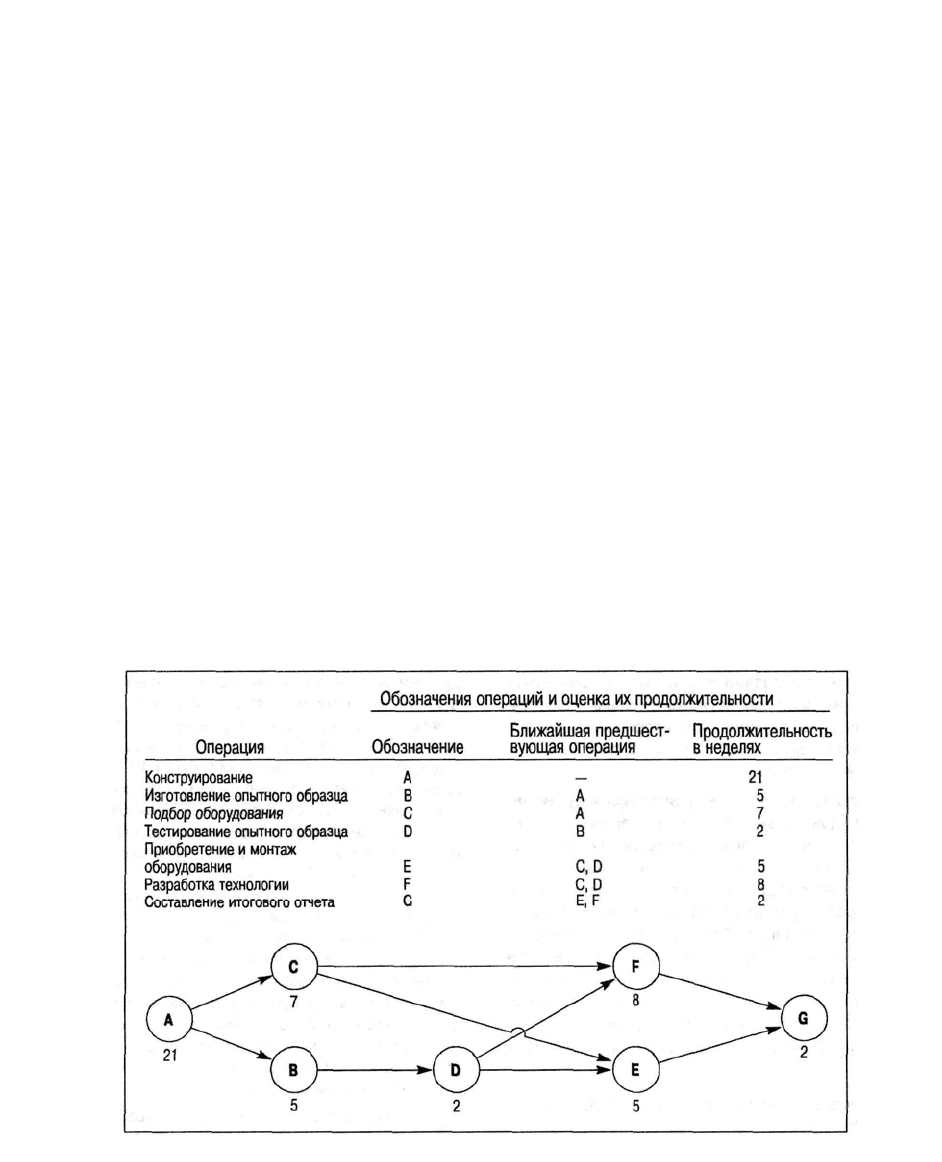
Рис. 3.2. Сетевой график проекта создания новой модели компьютера
82
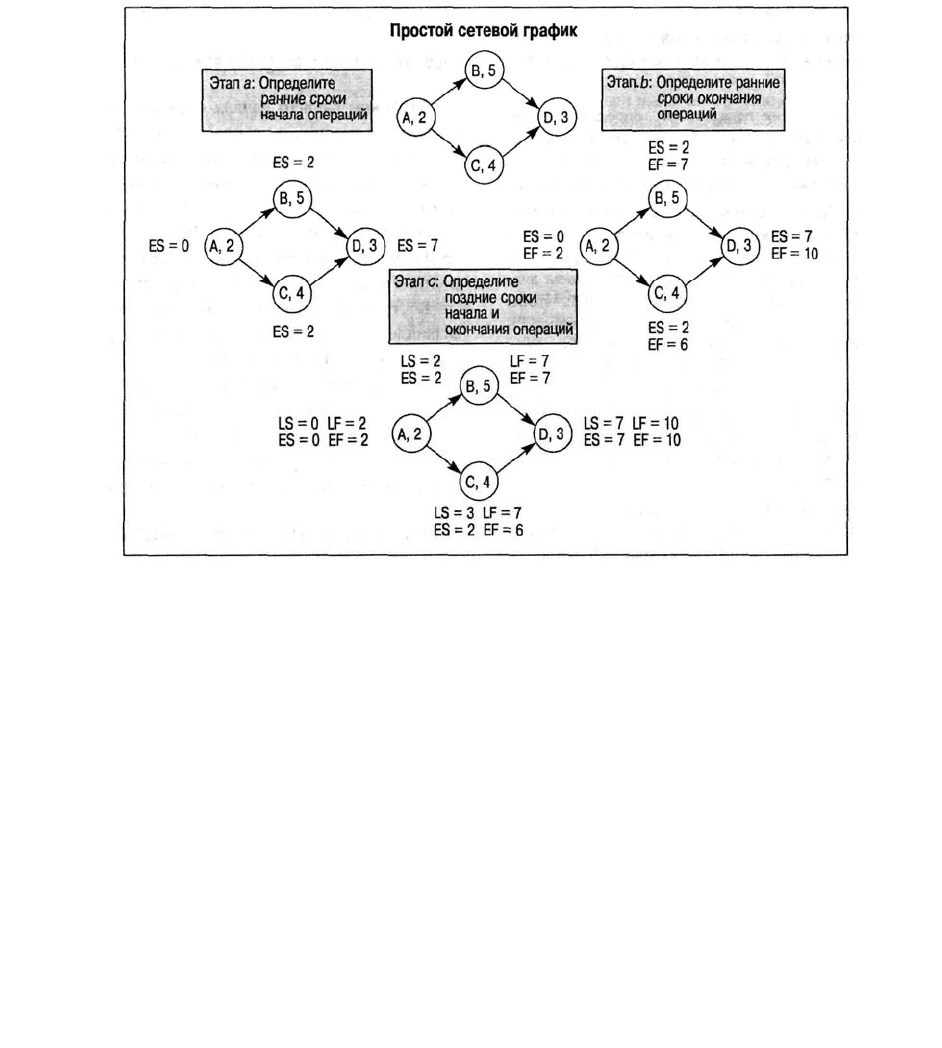
Рис. З.З. Этапы расчета параметров сетевого графика
Сетевой график на основе трех оценок продолжительности операций
ЕСЛИ однозначная оценка времени, необходимого для выполнения операции, является
ненадежным показателем, то используются три оценки. Они не только позволяют оценить
продолжительность операции, но и позволяют получить вероятностную оценку (Probability
Estimate) времени завершения всех операций, входящих в сетевой график. Кратко данную
процедуру можно описать следующим образом: оценка продолжительности операции (Estimated
Activity Time) представляет собой средневзвешенное значение, в котором больший вес приходится
на наиболее вероятную оценку, а меньший — на максимальную и минимальную
продолжительность. Как вы убедитесь дальше, обычно их значения соотносятся как 4, 1, 1.
Вероятностную оценку времени завершения всех операций в сетевом графике получают на основе
концепций базовой статистики, согласно которым вначале рассчитывают среднеквадратическое
отклонение последовательности операций, определяемое как корень квадрат- ный из суммы
дисперсии всех операции, лежащих на критическом пути. Затем это значение подставляется в
формулу аргумента функции Лапласа Z, описанную в п. 7 ниже, и для полученного значения Ж по
таблице вероятностей, приведенной в Приложении D, находят вероятность завершения проекта в
заданный срок.
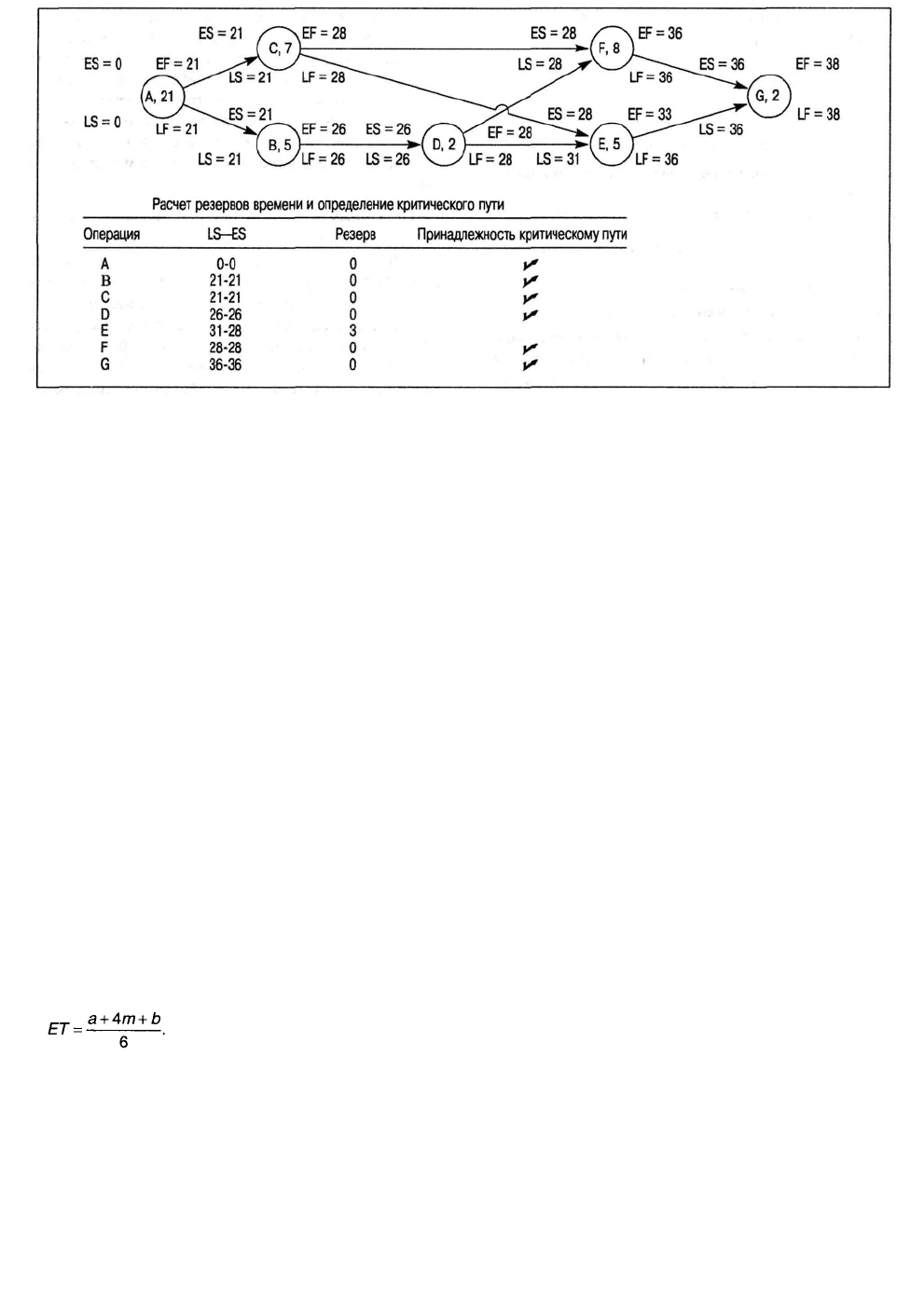
83
Рис. 3.4. Расчет параметров сетевого графика проекта создания новой модели компьютера
Пример 3.2. Три оценки продолжительности операций
В этом примере используются данные из примера 3.1, но продолжительность каждой операции
устанавливается на основе трех оценок.
Решение
1. Составьте перечень всех операций, которые нужно выполнить в ходе проекта.
2. Определите последовательность выполнения этих операций и постройте сетевой график,
отображающий эту последовательность.
3. Для определения продолжительности операций используются три следующие оценки:
а— оптимистическая оценка продолжительности: минимальный реальный период времени, в
течение которого может быть выполнена операция. (Существует очень небольшая вероятность,
которая обычно оценивается как 1%, что данная операция будет завершена в более короткие
сроки);
т— наиболее вероятная оценка продолжительности: наиболее точное предположение периода
времени, необходимого для выполнения конкретной операции. Поскольку т является наиболее
вероятной продолжительностью, это значение представляет собой также моду b-распределения, о
котором мы более подробно поговорим в п. 4;
b — пессимистическая оценка продолжительности: максимальный реальный период времени, в
течение которого операция должна быть выполнена. (Существует очень небольшая вероятность,
которая обычно оценивается как 1%, что выполнение данной операции займет больше времени).
Как правило, эти оценки даются непосредственными исполнителями конкретной операции.
Вычислите ожидаемое время (Expected Time) операции. Оно рассчитывается по формуле:
(3.1)
Этот расчет основан на статистической концепции в-распределения, согласно которой наиболее
вероятная оценка продолжительности операции (т) весит в 4 раза больше, чем оптимистическая
(а) или пессимистическая (о) оценки продолжительности распределение вероятностей отличается
универсальностью, оно может принимать разные формы и в упрощенной версии, позволяет прямо
вычислять среднее значение операции и среднеквадратическое отклонение.
5. Определите критический путь. Критический путь определяется так же, как в обсужденном
нами примере для однозначной оценки продолжительности операций, но с использованием
значений ожидаемого времени.
6. Вычислите дисперсию (σ
2
) продолжительности операции. Дисперсия (σ
2
) для ожидаемого
времени каждой операции вычисляется по формуле:
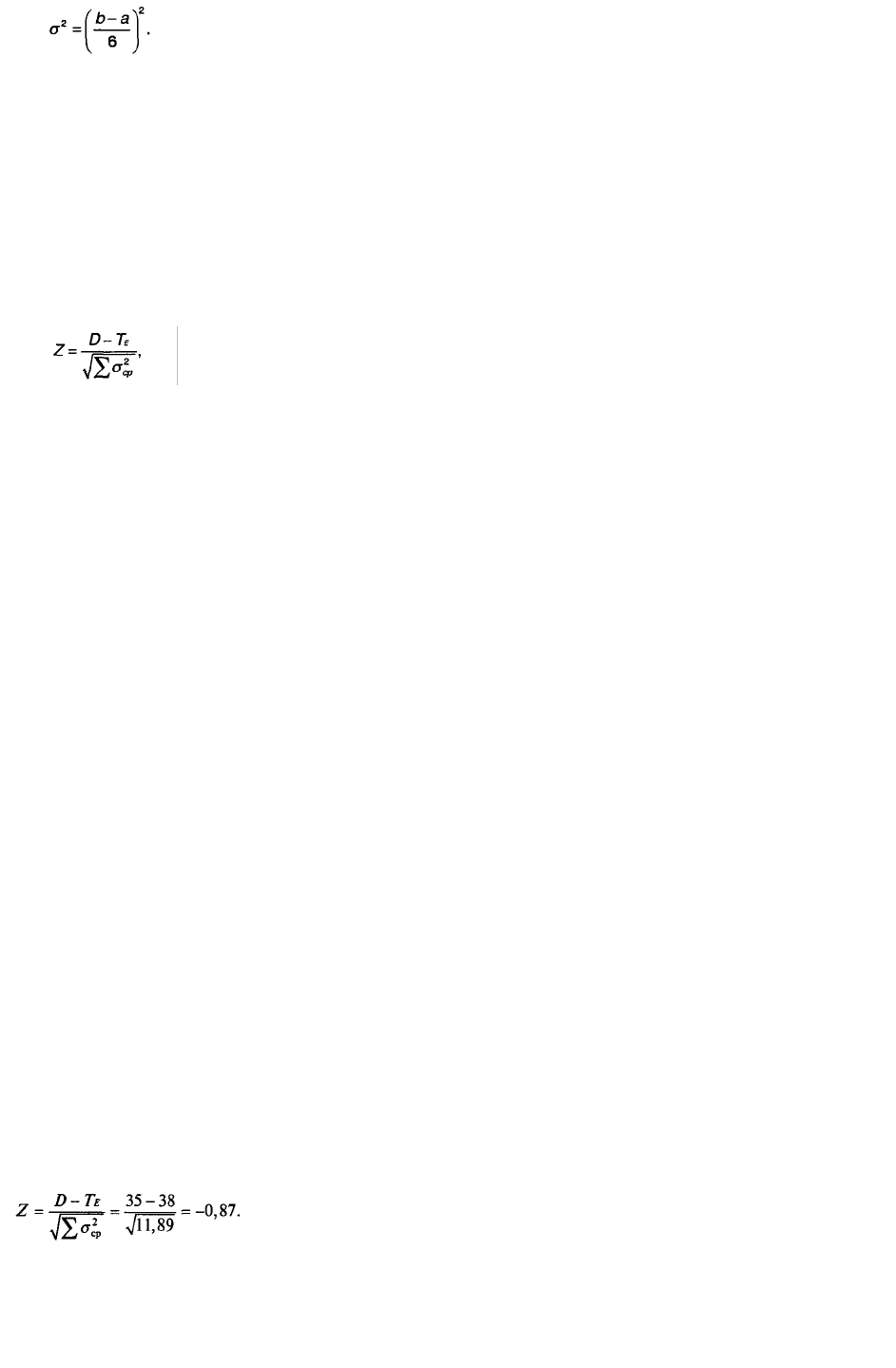
84
(3.2)
Как видно, дисперсия представляет собой квадрат разности двух крайних значений
продолжительности времени, разделенной на 6. Таким образом очевидно, что, чем больше эта
разница, тем больше значение дисперсии.
Определите вероятность завершения проекта в назначенный срок. Использование трех оценок
продолжительности операций дает возможность оценивать степень неопределенности срока
завершения проекта. Это осуществляется следующим образом:
a) сложите значения дисперсий всех операций, расположенных на критическом пути. (Случаи,
когда для проекта определено больше одного критического пути, описаны в следующем примере);
b) подставьте это значение, а также назначенный срок окончания проекта и ожидаемое время
завершения пропорции, лежащих на критическом пути;
где
D — назначенный срок окончания проекта;
Т
Е
— ожидаемое время завершения проекта. Ожидаемое время завершения проекта — это сумма
продолжительности всех операций, расположенных на критическом пути;
c) вычислите значение аргумента Z;
d) используя значение Z, определите вероятность завершения проекта в назначенный срок
(для этого следует воспользоваться таблицей нормального распределения вероятностей,
приведенной в Приложении Е).
Результаты выполнения всех описанных выше действий для нашего примера приведены в табл.
3.2.
Сетевой график проекта в данном случае аналогичен ранее построенному графику на рис. 3.4 с
той лишь разницей, что продолжительности операций являются средневзвешенными значениями.
Критический путь определяется так же, как было
описано выше, и его продолжительность используется по тому же назначению. Основное
различие между методом однозначной оценки продолжительности операций и методом с тремя
оценками (оптимистической, наиболее вероятной и пессимистической) заключается в том, что во
втором случае можно определить степень вероятности завершения проекта в заданные сроки. На
рис. 3.5 изображен итоговый сетевой график для рассматриваемого нами проекта со всеми
рассчитанными параметрами.
Поскольку в данном сетевом графике два критических пути, необходимо принять решение,
какие дисперсии следует использовать, чтобы максимально точно определить вероятность
выполнения проекта в заданный срок. Традиционный подход заключается в использовании пути с
наибольшей суммарной дисперсией, поскольку в этом случае внимание управленческого
персонала будет направлено на операции, которые имеют большой разброс оценок
продолжительности, а значит и обширную дисперсию. Следовательно, в нашем примере для
определения вероятности завершения проекта должны быть использованы дисперсии операций
А, С, F и G. Таким образом,
У σ
2
ср
= 9 + 2,78 + 0,11 + 0 = 11,89 . Предположим, что менеджер хочет узнать, насколько
вероятно завершить реализацию проекта за 35 недель, т.е. D = 35. Раньше было оп ределено, что
ожидаемое время окончания проекта составляет 38 недель. Подставив эти значения в формулу Z,
получаем
В соответствии с Приложением D находим, что значению Z= — 0,87 соответствует вероятность
0,19. Это означает, что менеджер проекта имеет лишь 19%-ный шанс выполнить проект в 35-
недельный срок. Обратите внимание, что данная степень вероятности характеризует, по сути,
только критический путь ACFG. Поскольку в сетевом графике есть еще один критический путь, а
также другие пути, которые в ходе реализации проекта тоже могут стать критическими,
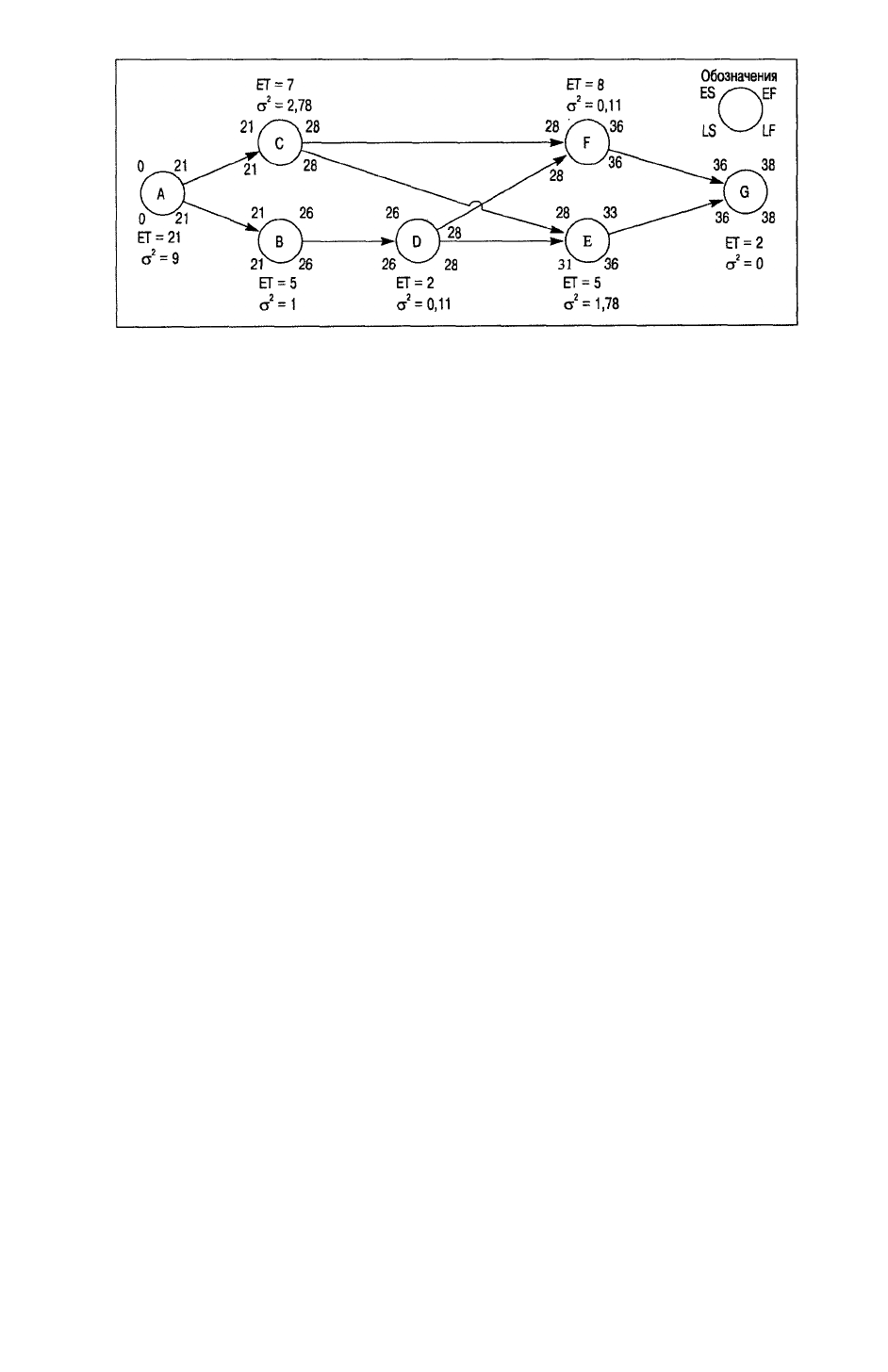
85
фактическая вероятность выполнения проекта за 35 недель будет меньше 0,19.
Рис 3.5. Итоговый сетевой график проекта создания новой модели компьютера, построенный
на основе трех оценок продолжительности операций
Текущая корректировка графиков проекта
Очень важно, чтобы фактическое выполнение графика проекта оставалось наиболее близким к
исходному графику на протяжении всего периода реализации проекта. На графике отображают
ход выполнения работ проекта, что позволяет обнаружить отклонения в тот момент, когда еще
есть время для их устранения. С их помощью также отслеживают, как расходуются средства, и
определяют даты проведения частичных платежей. И все же нередки случаи, когда за
выполнением графика следят без должного внимания или вообще его игнорируют.
Недавно проведенное исследование, посвященное работе менеджеров проектов, подтвердило,
что в этой сфере на пути к успеху существует немало возможных препятствий (врезка "Типичные
проблемы менеджеров проектов").
Модели типа "время-затраты"
На практике менеджеры проектов уделяют затратам не меньше внимания, чем сроку
выполнения проекта. В связи с этим были разработаны так называемые модели типа "время—
затраты" (Time-Cost Models). Эти модели представляют собой расширенный вариант методов
PERT и СРМ и используются для создания графиков минимальных затрат (Minimum-Cost
Schedule) для всего проекта в целом и контроля над расходами в ходе реализации проекта.
Составление сетевого графика с минимальными затратами (компромисс время-затраты)
Основной предпосылкой составления графика минимальных затрат является то, что между
сроком выполнения операции и стоимостью проекта существует определенная взаимосвязь. Если
нужно ускорить выполнение операции, то затрачиваются дополнительные средства на такое
ускорение операции, сохраняя при этом средства на поддержание (либо продолжение) проекта.
Затраты, связанные с досрочным выполнением операций, получили название прямых издержек
операций (Activity Direct Costs), и они увеличивают издержки по проекту в целом. Такие издержки
обычно связаны с рабочей силой, например затраты на оплату сверхурочной работы, наем
дополнительных работников, перемещение рабочих с других операций; либо с ресурсами: закупка
или аренда дополнительного или более эффективного оборудования и использование
дополнительных вспомогательных устройств и приспособлений.
Издержки, связанные с поддержанием проекта, называют косвенными издержками проекта
(Project Indirect Costs). К ним относятся накладные расходы, расходы на содержание
производственных помещений, дополнительные издержки в виде перерасходов каких-либо
ресурсов (Resource Opportunity Costs), а также, в определенных контрактных ситуациях, издержки
на выплату штрафов или на неучтенные поощрительные платежи. Поскольку прямые издержки
операций и косвенные издержки проекта на протяжении проекта действуют разнонаправленно,
при составлении графика затрат очень важно определить такую продолжительность проекта, при
которой они были бы сведены к минимуму, или, иными словами, найти золотую середину в
компромиссе время—затраты.
Процесс поиска такого компромисса состоит из пяти описанных дальше этапов. Для их
пояснения рассмотрим простой сетевой график, состоящий из четырех операций, взятых из

86
графика, изображенного на рис. 3.3. Наш новый график показан на рис. 3.6.
Предположим также, что косвенные издержки остаются неизменными на протяжении восьми
дней, а затем увеличиваются на 5 долларов в день.
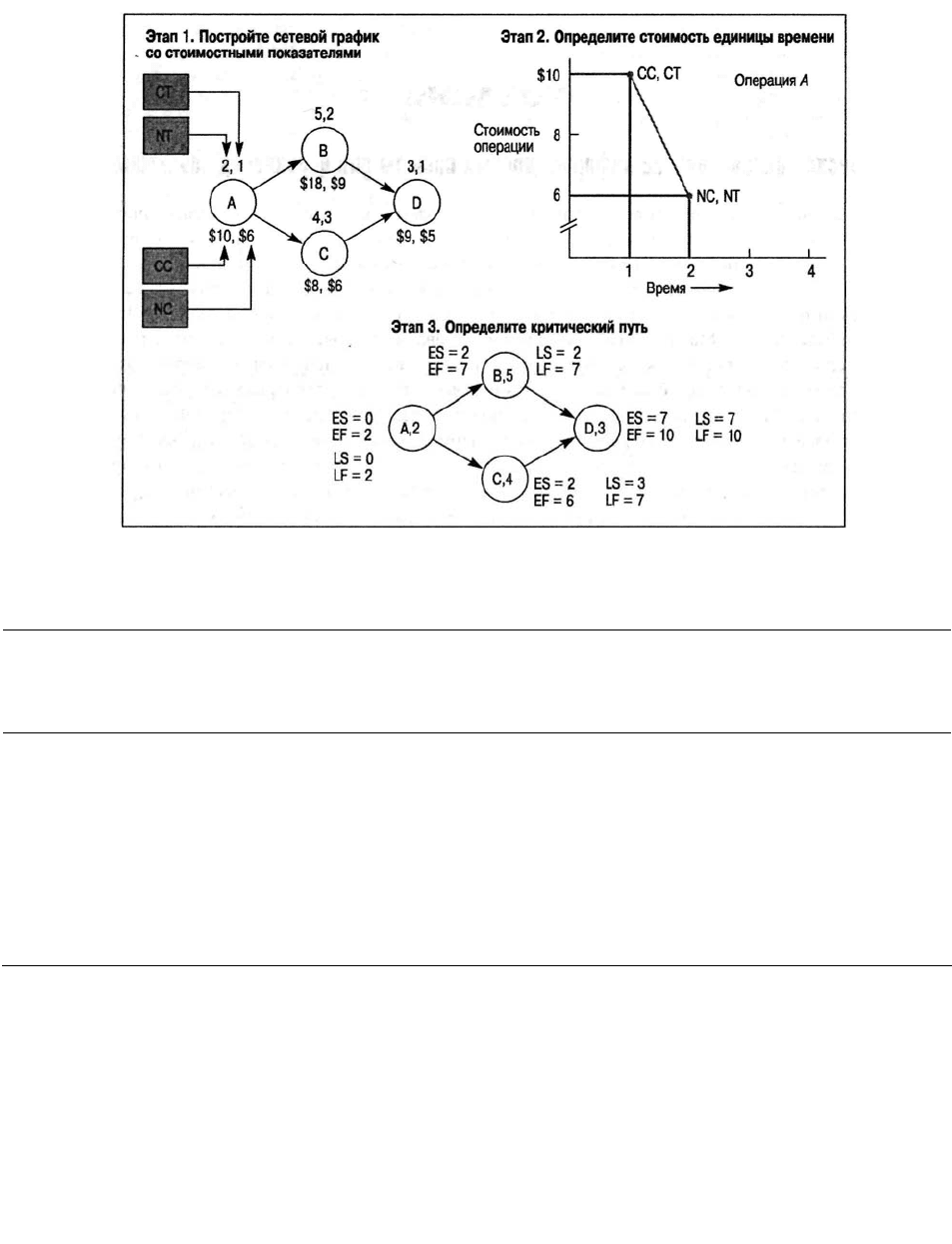
1. Постройте сетевой график. Этот график должен включать следующие данные по каждой
операции:
a) нормальная стоимость (Normal Cost — NQ, т.е. наименьшая ожидаемая стоимость данной
операции. (На графике это меньшее из двух числовых показателей затрат, указанных под каждым
узлом на рис. 3.6 );
b) нормальный срок (Normal Time — NT), время, соответствующее нормальной стоимости;
c) продолжительность досрочного выполнения операции (Crash Time — СТ), наименьший
срок, в течение которого можно выполнить операцию;
d) стоимость досрочного выполнения операции (Crash Cost — CQ, т.е. стоимость,
соответствующая ускоренному выполнению операции.
2. Определите приращение стоимости при досрочном выполнении каждой операции за
единицу времени (предположим, за день). Взаимосвязь между временем выполнения операции и ее
стоимостью можно графически отобразить, нанеся координаты СС и СТ на графике и соединив их
с координатами NT и NC с помощью выпуклой, вогнутой или прямой линии, либо каким-либо
другим способом, в зависимости от структуры фактической себестоимости выполнения операции.
В нашем примере на рис. 3.6 для всех операций примем линейную связь между
продолжительностью и стоимостью. Такое допущение очень часто применяется на практике,
поскольку оно упрощает определение дневного приращения стоимости при досрочном
выполнении операции.
Типичные проблемы менеджеров проектов
Несмотря на то, что 84% менеджеров проектов отвечают за то, чтобы управляемый ими проект
не выходил за рамки бюджета, на решение этой задачи они затрачивают не более 15% рабочего
времени. Согласно данным обзора работы менеджеров проектов, составленного агентством Zweig
White & Associates (г. Натрик, штат Массачусетс), 16% менеджеров не всегда даже знают, какой
именно бюджет выделен на реализацию их проекта.
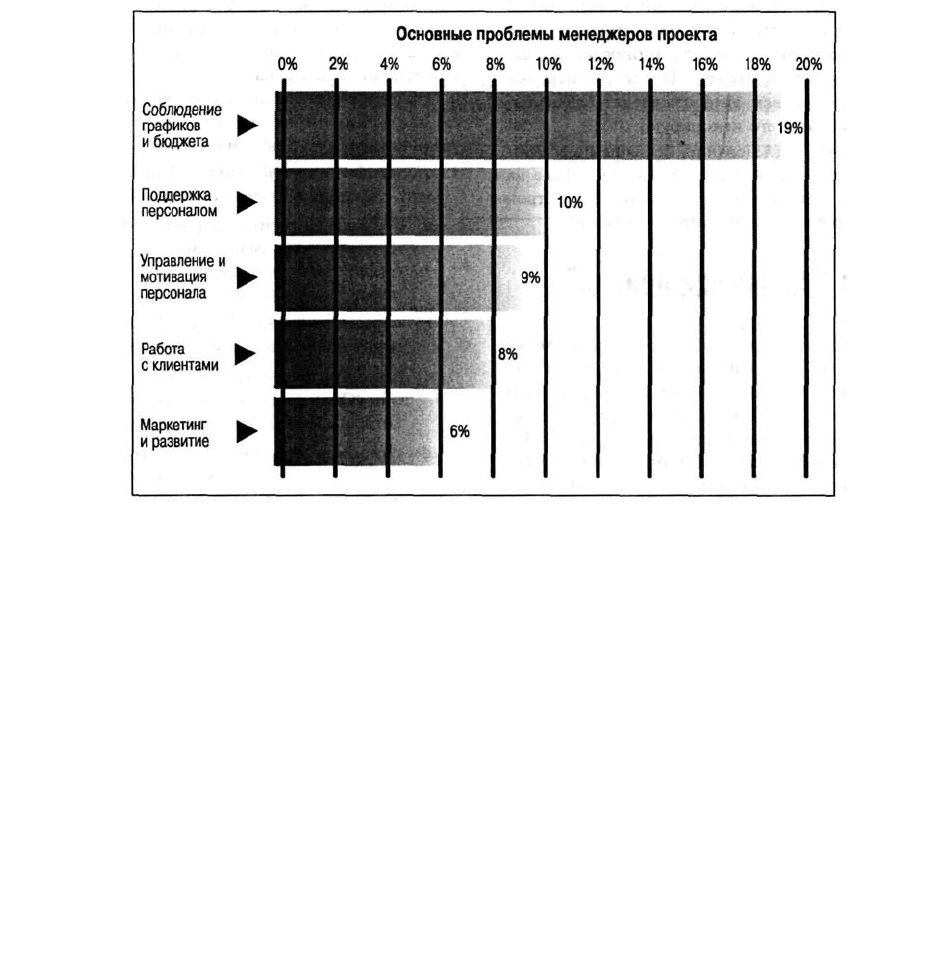
Данное исследование также показало, что многие менеджеры проектов (19%) считают самой
сложной своей задачей выполнение графиков и бюджетов. Это положение в определенной степени
можно отнести на счет двух аспектов работы, на которые менеджеры жалуются чаще всего:
недостаточная или неадекватная поддержка персонала (10%) и ответственность без полномочий
(9%).
Вообще менеджеры назвали несколько основных причин, которые мешают им работать в
полную силу; 17% заявили, что членам проектной группы редко либо никогда не позволяют
ознакомиться с их конкретной долей участия в проекте. Кроме того, они зачастую не имеют
достаточной подготовки. Только 26% из опрошенных фирм проводят обязательное обучение
менеджеров проектов; 40% делают это на факультативной основе, а 29% не делают этого вообще.
И даже в компаниях, обучающих своих менеджеров, уровень обучения зачастую
неудовлетворителен. И лишь меньше половины менеджеров проектов получили подготовку к
выполнению основных задач, таких как открытие и внесение новых заданий, отслеживание хода
работ и составление бюджета.
87
Источник. "Project Managers Challenges", HE Solutions, December 1996, p. 9.
Его, в этом случае, можно легко получить через наклон прямой по следующей формуле:
CC-NC Наклон =NT-CT
Если допущение о линейном характере этой взаимосвязи неправильно, стоимость досрочного
выполнения операции придется определять графически для каждого дня операции, на который ее
можно уменьшить. Вычисления дневного приращения стоимости при ускорении выполнения всех
операции рассматриваемого нами проекта приведены в табл. 3.3.
3. Определите критический путь. В нашем простом примере сетевого графика критический
путь составит 10 дней. На критическом пути будут расположены операции А, В и D.
4. Сократите критический путь с наименьшим приростом стоимости. Самый простой метод
выполнения этой задачи заключается в следующем: начните с исходного нормального графика,
сократите его критический путь на один день, удалив его из операции с наименьшей стоимостью.
Затем проведите перерасчет, определите новый критический путь и опять сократите его на один
день. Повторяйте эту процедуру до тех пор, пока продолжительность проекта не станет отвечать
вашим потребностям, либо до того момента, когда этот срок уже нельзя будет сократить. В табл.
3.4 отображен ряд последовательных сокращений сетевого графика на один день.
88
Рис. З.6. Пример процедуры поиска компромисса время—затраты
Таблица 3.3. Вычисление дневного приращения стоимости при досрочном выполнении
операций
Операция
CC-NC
NT-CT
CC-NC
NT-CT
Дневное приращение
стоимости
при досрочном выполнении
Число дней, на
которое можно
сократить
операцию
А
$10-6
2-1
$10-6
$4
1
В $18-9 5-2 $18-9 $3 3
С
$8-6
4-3
$8-6
$2
1
D $9-5 3-1 $9-5 $2 2
*Чтобы сократить путь на один день, обе операции В и С должны быть выполнены досрочно.
5. Постройте графики прямых, косвенных и общих издержек и найдите точку минимальных
суммарных затрат. На рис. 3.7 представлены такие графики для нашего примера, причем
принято, что косвенные затраты сохраняются неизменными (10 долларов в день) на протяжении
восьми дней, а в последующих два дня увеличиваются ежедневно на 5 долларов. График прямых
издержек построен на основе данных из табл. 3.4.
Сложив косвенные и прямые издержки каждого дня, вы получите кривую общей стоимости
проекта. Как видно из рис. 3.7, минимальное значение (40 долларов, т.е. 30 долларов прямых
издержек, плюс 10 долларов косвенных) этой кривой приходится на восьмой день.

89
0 5 6 7 8 9 10
Продолжительность (дни)
Рис. 3.7. Графики издержек и минимальная стоимость
НОВАЦИЯ
Практическое использование информационных систем для управления проектами
В 90-х годах произошел резкий всплеск интереса к методам и концепциям управления
проектами, который сопровождался значительным ростом предложения всевозможного
специального программного обеспечения. Всего десять лет назад существовало лишь несколько
пакетов таких программ, а на сегодня разработано свыше 100 информационных систем для
управления проектами, и применение их растет в геометрической прогрессии. Так, например,
сегодня на наши курсы менеджмента уровня MBA (Master of Business Administration —
Магистратура экономики управления) почти половина студентов приходят, имея опыт
пользователя такого программного обеспечения; а все остальные умеют работать как минимум в
одной программе и обладают базовыми знаниями о нескольких других (таких как Microsoft Project
for Windows, Primavera Project Planner, Time Line, Project Scheduler, Milestone, Schedule Publisher,
Texim Project). В начале 90-х годов опыт работы с информационными системами для управления
проектами имели один-два студента в группе, а единственная программа, которой мы обучали, не
предусматривала управление издержками и распределение ресурсов по уровням, в ней даже нельзя
было создать график PERT или Ганта. Предлагаем вашему вниманию краткое описание трех
основных информационных систем, которые отлично справляются с этими задачами.
Программа Microsoft Project распространяется с отличным электронным учебным пособием,
что является одной из причин ее огромной популярности среди менеджеров, управляющих
проектами средней величины. Данный пакет позволяет составлять графики расходования
ресурсов, распределять ресурсы по уровням и между операциями, а также осуществлять контроль
издержек и создавать графики и отчеты, полностью готовые к использованию. На рис. 3.8 вы
видите один из примеров использования программы Microsoft Project.
Если же основной вашей целью является составление графика, советуем воспользоваться
программой Milestone, Etc. компании Kidasa. Созданные с ее помощью графики Ганта способны
отображать даже взаимозависимость между операциями по мере развертывания проекта, и, если в
ходе реализации проекта графики нуждаются в обновлении, данные о начале и окончании
операций в них легко заменяются новыми.
И наконец, при работе над очень крупными проектами или даже программами, состоящими из
нескольких проектов, чаще других используется программа Primavera Project Planner. Так,
например, именно ее выбрали для управления многомиллионным проектом восстановления
Центра мировой торговли, разрушенного террористами 26 февраля 1993 года (более подробное
описание ее использования представлено в начале данной главы). Программа анализа риска для
казино Монте-Карло, также созданная компанией Primavera, использовалась для определения
того, каким временем и суммами следует рисковать при различных допущениях.
Несомненно, вас заинтересует новейшая информация о последних программных продуктах
этой компании. Вы можете ознакомиться с ней на Web-сервере компании Primavera Systems, Inc.
по адресу http://www.primavera.com.

90
Таблица 3.4. Последовательное сокращение продолжительности проекта на один день
Текущий
критически
й путь
Оставшееся
количество дней, на
которое можно
сократить операцию
Дневное приращение
стоимости при
досрочном выполнении
операции
Операция с
наименьшей
стоимостью,
подлежащая
ускорению
Общая
стоимость всех
операций в
сетевом графике
($)
Продолжитель
н ость
проекта (дней)
ABD Нормальные сроки и
стоимости всех
операций
26
10
ABD А-1, В-3, D-2 А-4, В-3, D-2 D
28
9
ABD А-1.В-3, D-1 А-4, В-3, D-2 D
30
8
ABD А-1, В-3 А-4, В-3 В
33
7
ABCD А-1, В-2, С-1 А-4, В-3, С-2 А*
37
6
ABCD В-2, С-1 В-З.С-2 В и С**
42
5
ABCD В-1 В-3 В
45
5
*Чтобы сократить критический путь на один день, сократите либо одну операцию А, либо операции В и
С одновременно (поскольку сокращение операций В и С по отдельности приведет не к укорачиванию, а к
изменению критического пути).
** Чтобы сократить путь на один день, обе операции В и С должны быть выполнены досрочно.
Puc. 3.8. Пример графика Ганша, созданного с помощью программы Microsoft Project
