Chow T.L. Mathematical Methods for Physicists: A Concise Introduction

Подождите немного. Документ загружается.

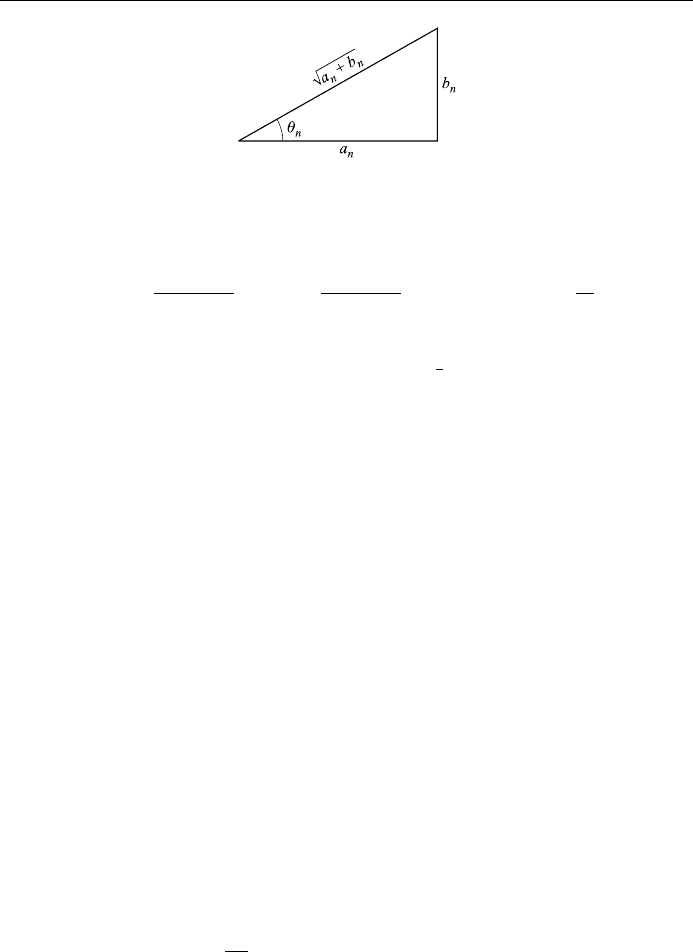
Now let (see Fig. 4.8)

cos 





 b

; sin 





 b

; so 

 tan

ÿ1



;





 b

; C



;

then we have the trigonometric identity

cos nx  b

sin nx  C

cos nx ÿ 

;

and accordingly the Fourier series becomes

f xC



n1

cos nx ÿ 

: 4:12

In this new form, the Fourier series represents a periodic function as a sum of

sinusoidal components having diÿerent frequencies. The sinusoidal component of

frequency n is called the n th harmonic of the periodic function. The ®rst har-

monic is commonly called the fundamental component. The angles 

and the

coecients C

are known as the phase angle and amplitude.

Using Euler's identities e

i

 cos   i sin  where i

ÿ1, the Fourier series

for f x can be converted into complex form

f x

nÿ1

inx=L

; 4:13a

where

n

 a

þ ib



ÿL

f xe

ÿinx=L

dx; for n > 0: 4:13b

Eq. (4.13a) is obtained on the understanding that the Dirichlet conditions are

satis®ed and that f x is continuous at x.Iff x is discontinuous at x, the left

hand side of Eq. (4.13a) should be replaced by f x  0f x ÿ 0=2.

The exponential form (4.13a) can be considered as a basic form in its own right:

it is not obtained by transformation from the trigonometric form, rather it is

156

FOURIER SERIES AND INTEGRALS

Figure 4.8.

constructed directly from the given function. Furthermore, in the complex repre-

sentation de®ned by Eqs. (4.13a) and (4.13b), a certain symmetry between the

expressions for a function and for its Fourier coecients is evident. In fact the

expressions (4.13a) and (4.13b) are of essentially the same structure, as the follow-

ing correlation reveals:

x  L; f xc

 cn; e

inx=L

 e

ÿinx=L

;

nÿ1



ÿL

dx:

This duality is worthy of note, and as our development proceeds to the Fourier

integral, it will become more striking and fundamental.

Integration and diÿerentiation of a Fourier series

The Fourier series of a function f x may always be integ rated term-by-term to

give a new series which converges to the integral of f x.Iff x is a continuous

function of x for all x, and is periodic (of period 2) outside the interval

ÿ<x <, then term-by-term diÿerentiation of the Fourier series of f x

leads to the Fourier series of f

x, provided f

x satis®es Dirichlet's conditions.

Vibrating strings

The equation of motion of transverse vibratio n

There are numerous applications of Fourier seri es to solutions of boundary value

problems. Here we consider one of them, namely vibrating strings. Let a string of

length L be held ®xed between two points (0, 0) and (L, 0) on the x-axis, and then

given a transverse displacement parallel to the y-axis. Its subsequent motion, with

no external forces acting on it, is to be considered; this is described by ®nding the

displacement y as a function of x and t (if we consider only vibration in one plane,

and take the xy plane as the plane of vibration). We will assume that , the mass

per unit length is unifor m over the entire length of the string, a nd that the string is

perfectly ¯exible, so that it can transmit tension but not bending or shearing

forces.

As the string is drawn aside from its position of rest along the x-axis, the

resulting increase in length causes an increase in tension, denoted by P. This

tension at any point along the string is always in the direction of the tangent to

the string at that point. As shown in Fig. 4.9, a force PxA acts at the left hand

side of an element ds, and a force Px  dxA acts at the right hand side, where A

is the cross-sectional area of the string. If  is the inclination to the horizontal,

then

 AP cos  dÿAP cos ; F

 AP sin  dÿAP sin :

157

INTEGRATION AND DIFFERENTIATION OF A FOURIER SERIES

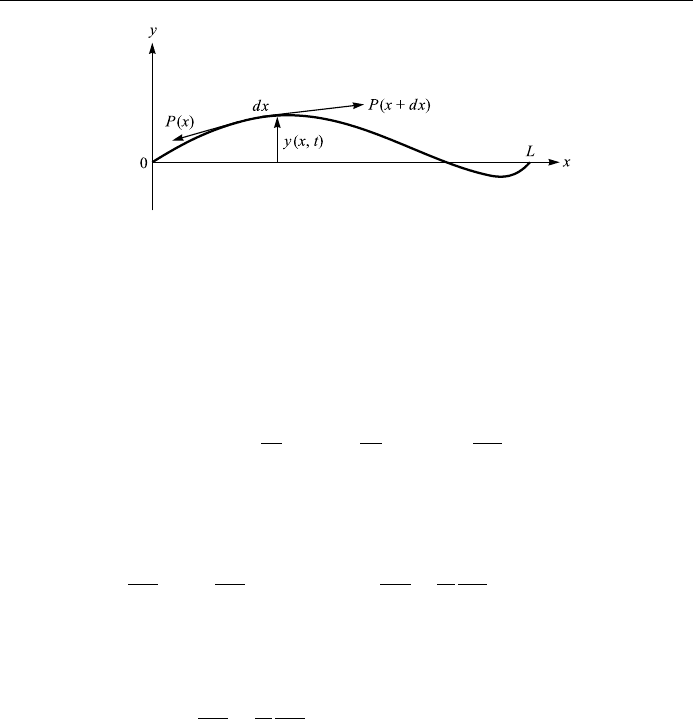
We limit the displacement to small values, so that we may set

cos   1 ÿ 

=2; sin     tan   dy=dx;

then

 AP



xdx





 AP

dx:

Using Newton's second law, the equation of motion of transverse vibration of the

element becomes

Adx

 AP

dx; or



; v 



P=

Thus the transverse displacement of the string satis®es the partial diÿerential wave

equation



; 0 < x < L; t > 0 4:14

with the following boundary conditions: y0; tyL; t0;@y=@t  0;

yx; 0f x; where f  x describes the initial shape (position) of the string,

and v is the velocity of propagation of the wave along the string.

Solution of the wav e equation

To solve this boundary value problem, let us try the method of separation vari-

ables:

yx; tXxTt: 4:15

Substituting this into Eq. (4.14) yields

1=Xd

X=dx

1=v

Td

T=dt

.

158

FOURIER SERIES AND INTEGRALS

Figure 4.9. A vibrating string.

Since the left hand side is a function of x only and the right hand side is a function

of time only, they must be equal to a common separation constant, which we will

call ÿ

. Then we have

X=dx

ÿ

X; X0XL0 4:16a

and

T=dt

ÿ

TdT=dt  0att  0: 4:16b

Both of these equations are typical eigenvalue problems: we have a diÿerential

equation containing a parameter , and we seek solutions satisfying certain

boundary conditions. If there are special values of  for which non-trivial solu-

tions exist, we call these eigenvalues, and the corresponding solutions eigensolu-

tions or eigenfunctions.

The general solution of Eq. (4.16a) can be written as

XxA

sinxB

cosx:

Applying the boundary conditions

X00 ) B

 0;

and

XL0 ) A

sinL0

 0 is the trivial solution X  0 (so y  0); hence we must have sinL0,

that is,

L  n; n  1; 2; ...;

and we obtain a series of eigenvalues



 n=L; n  1; 2; ...

and the corresponding eigenfunctions

xsinn=Lx; n  1; 2; ... :

To solve Eq. (4.16b) for Tt we must use one of the values 

found above. The

general solution is of the form

TtA

cos

vtB

sin

vt:

The boundary condition leads to B

 0.

The general solution of Eq. (4.14) is hence a linear superposition of the solu-

tions of the form

yx; t

n1

sinnx=Lcosnvt=L; 4:17

159

VIBRATING STRINGS

the A

are as yet undetermined constants. To ®nd A

, we use the boundary

condition yx; tf x at t  0, so that Eq. (4.17) reduces to

f x

n1

sinnx=L:

Do you recognize the in®nite series on the right hand side? It is a Fourier sine

series. To ®nd A

, mult iply both sides by sin(mx=L) and then integrate with

respect to x from 0 to L and we obtain



f xsinmx=Ldx; m  1; 2; ...

where we have used the relation

sinmx=Lsinnx= Ldx 



Eq. (4.17) now gives

yx; t

n1

f xsin

nx



sin

nx

cos

nvt

:  4 :18

The terms in this series represent the natural modes of vibration. The frequency

of the nth normal mode f

is obtained from the term involving cosnvt=L and is

given by

2f

 nv=L or f

 nv=2L:

All frequencies are integer multiples of the lowest frequency f

.Wecallf

the

fundamental frequency or ®rst harmonic, and f

and f

the second and third

harmonics (or ®rst and second overtones) and so on.

RLC circu it

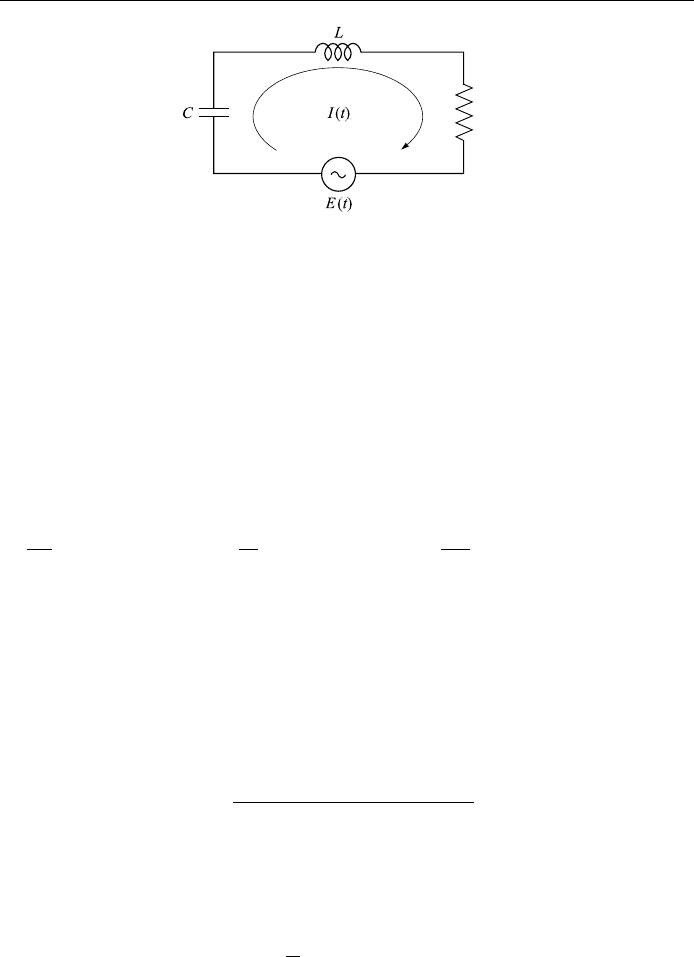
Another good example of application of Fourier series is an RLC circuit driven by

a variable voltage Et which is periodic but not necessarily sinusoidal (see Fig.

4.10). We want to ®nd the current It ¯owing in the circuit at time t.

According to Kirchhoÿ 's second law for circuits, the impressed voltage Et

equals the sum of the voltage drops across the circuit components. That is,

 RI 

 E t;

where Q is the total charge in the capacitor C. But I  dQ=dt, thus diÿerentiating

the above diÿerential equation once we obtain

 R



I 

160

FOURIER SERIES AND INTEGRALS

Under steady-state conditions the current It is also periodic, with the same

period P as for Et. Let us assume that both Et and It possess Fourier

expansions and let us write them in their complex forms:

Et

nÿ1

in!t

; It

nÿ1

in!t

!  2=P:

Furthermore, we assume that the series can be diÿerentiated term by term. Thus



nÿ1

in!E

in!t

;



nÿ1

in!c

in!t

;



nÿ1

ÿn

c

in!t

Substituting these into the last (second-order) diÿerential equation and equating

the coecients with the same exponential e

int

, we obtain

ÿn

L  in!R  1=C

ÿ

 in!E

Solving for c



in!=L

 1=CL

ÿn

iR=Ln!

Note that 1/LC is the natural frequency of the circuit and R/L is the attenuation

factor of the circuit. The Fourier coeci ents for Et are given by



P=2

ÿP=2

Ete

ÿin!t

dt:

The current It in the circuit is given by

It

nÿ1

in!t

161

RLC CIRCUIT

Figure 4.10. The RLC circuit.

Orthogonal functions

Many of the properties of Fourier series considered above depend on orthogonal

properties of sine and cosine functions

sin

mx

sin

nx

dx  0 ;

cos

mx

cos

nx

dx  0 m 6 n:

In this section we seek to generalize this orthogonal property. To do so we ®rst

recall some elementary properties of real vector s in three-dimensional space.

Two vectors A and B are called orthogonal if A  B  0. Although not geome-

trically or physically obvious, we generalize these ideas to think of a function, say

Ax, as being an in®nite-dimensional vector (a vector with an in®nity of compo-

nents), the value of each component being speci®ed by substituting a particular

value of x taken from some interval (a, b), and two functions, Ax and Bx are

orthogonal in (a, b)if

AxBxdx  0: 4:19

The left-side of Eq. (4.19) is called the scalar product of Ax and Bx and

denoted by, in the Dirac bracket notation, hAxjBxi. The ®rst factor in the

bracket notation is referred to as the bra and the second factor as the ket, so

together they comprise the bracket.

A vector A is called a unit vector or normalized vector if its magnitude is unity:

A  A  A

 1. Extending this concept, we say that the function Ax is normal

or normalized in (a, b)if

hAxjAxi 

AxAxdx  1: 4:20

If we have a set of functions '

x; i  1; 2; 3; ...; having the propert ies

x

xi 

x'

xdx  

; 4:20a 

where 

is the Kronecker delta symbol, we then call such a set of functions an

orthonormal set in (a, b). For example, the set of functions '

x

2=

1=2

sinmx; m  1; 2; 3; ... is an orthonormal set in the interval 0  x  .

Just as in three-dimensional vector space, any vector A can be expanded in the

form A  A

 A

, we can consider a set of orthonormal functions '

as base vectors and expand a function f x in terms of them, that is,

f x

n1

x a  x  b; 4:21

162

FOURIER SERIES AND INTEGRALS

the series on the right hand side is called an orthonormal series; such series are

generalizations of Fourier series. Assuming that the series on the right converges

to f x, we can then multiply both sides by '

x and integrate both sides from a

to b to obtain

hf xj'

xi 

f x'

xdx;  4 :21a

can be called the generalized Fourier coecients.

Multiple Fourier series

A Fourier expansion of a function of two or three variables is often very useful in

many applications. Let us consider the case of a function of two variables, say

f x; y. For example, we can expand f x; y into a double Fourier sine series

f x; y

m1

n1

sin

mx

sin

ny

; 4:22

where



f x; ysin

mx

sin

ny

dxdy: 4:22a

Similar expansions can be made for cosine series and for series having both sines

and cosines.

To obtain the coecients B

, let us rewrite f x; y as

f x; y

m1

sin

mx

; 4:23

where



n1

sin

ny

: 4:23a

Now we can consider Eq. (4.23) as a Fourier series in which y is kept constant

so that the Fourier coecients C

are given by



f x; ysin

mx

dx: 4:24

On noting that C

is a function of y, we see that Eq. (4.23a) can be considered as a

Fourier series for which the coecients B

are given by



sin

ny

dy:

163

MULTIPLE FOURIER SERIES

Substituting Eq. (4.24) for C

into the above equation, we see that B

is given by

Eq. (4.22a).

Similar results can be obtained for cosine series or for series containing both

sines and cosines . Furthermore, these ideas can be generalized to triple Fourier

series, etc. They are very useful in solving, for example, wave propagation and

heat conduction problems in two or three dimensions. Because they lie outside of

the scope of this book, we have to omit these interesting applications.

Fourier integrals and Fourier transforms

The properties of Fourier series that we have thus far developed are adequate for

handling the expansion of any periodic function that satis®es the Dirichlet con-

ditions. But many problems in physics and engineering do not involve periodic

functions, and it is therefore desirable to general ize the Fourier series method to

include non-periodic functions. A non-periodic function can be considered as a

limit of a given periodic function whose period becomes in®nite, as shown in

Examples 4.5 and 4.6.

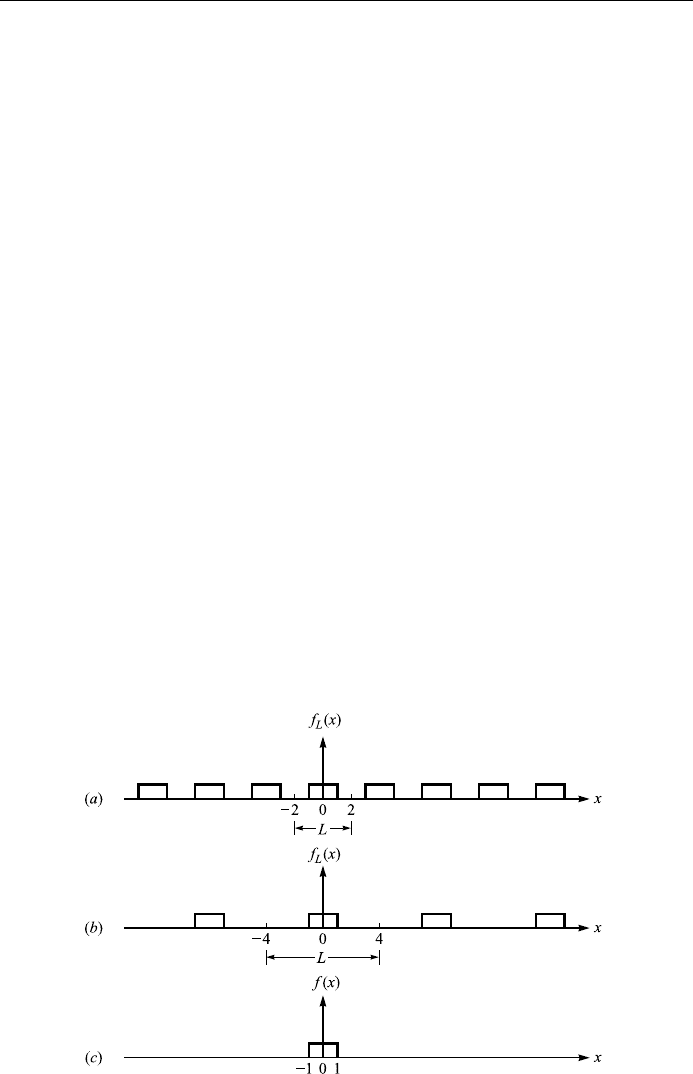
Example 4.5

Consider the periodic functions f

x

x

0 when ÿL=2 < x < ÿ1

1 when ÿ1 < x < 1

0 when 1 < x < L=2

;

164

FOURIER SERIES AND INTEGRALS

Figure 4.11. Square wave function: a L  4; b L  8; c L !1.

which has period L > 2. Fig. 4.11(a) shows the function when L  4. If L is

increased to 8, the functio n looks like the one shown in Fig. 4.11(b). As

L !1we obtain a non-periodic function f x, as shown in Fig. 4.11(c):

f x

1 ÿ1 < x < 1

0 otherwise



Example 4.6

Consider the periodic function g

x (Fig. 4.12(a)):

xe

ÿjxj

when ÿL=2 < x < L=2:

As L !1we obtain a non-periodic function gx: gxlim

L!1

x (Fig.

4.12(b)).

By investigating the limit that is approached by a Fourier series as the period of

the given function becomes in®nite, a suitable representation for non-periodic

functions can perhaps be obtained. To this end, let us write the Fourier series

representing a periodic function f x in complex form:

f x

nÿ1

i!x

; 4:25



ÿL

f xe

ÿi!x

dx 4: 26 

where ! denotes n=L

! 

n

; n positive or negative: 4: 27 

The transition L !1is a little tricky since c

apparently approaches zero, but

these coecients should not approach zero. We can ask for help from Eq. (4.27),

from which we have

! =Ln;

165

FOURIER INTEGRALS AND FOURIER TRANSFORMS

Figure 4.12. Sawtooth wave functions: aÿL=2 < x < L=2; b L !1.