Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


and the `adjacent' values of ! are obtained by sett ing n 1, which corresponds
to
L=! 1:
Then we can multiply each term of the Fourier series by L=! and obtain
f x
X
1
nÿ1
L
c
n
e
i!x
!;
where
L
c
n
1
2
Z
L
ÿL
f xe
ÿi!x
dx:
The troublesome factor 1=L has disappeared. Switching completely to the !
notation and writing L=c
n
c
L
!, we obtain
c
L
!
1
2
Z
L
ÿL
f xe
ÿi!x
dx
and
f x
X
1
L!=ÿ1
c
L
!e
i!x
!:
In the limit as L !1, the !s are distributed continuously instead of discretely,
! ! d! and this sum is exactly the de®nition of an integral. Thus the last
equations become
c! lim
L!1
c
L
!
1
2
Z
1
ÿ1
f xe
ÿi!x
dx 4:28
and
f x
Z
1
ÿ1
c!e
i!x
d!: 4:29
This set of formulas is known as the Fourier transformation, in somewhat diÿer-
ent form. It is easy to put them in a symmetrical form by de®ning
g!
2
p
cÿ!;
then Eqs. (4.28) and (4.29) take the symmetrical form
g!
1
2
p
Z
1
ÿ1
f x
0
e
ÿi!x
0
dx
0
; 4:30
f x
1
2
p
Z
1
ÿ1
g!e
i!x
d!: 4:31
166
FOURIER SERIES AND INTEGRALS

The function g! is called the Fourier transform of f x and is written
g!Fff xg. Eq. (4.31) is the inverse Fourier transform of g! and is written
f xF
ÿ1
fg!g; sometimes it is also called the Fourier integral representation
of f x. The expon ential function e
ÿi!x
is sometimes called the kernel of trans-
formation.
It is clear that g! is de®ned only if f x satis®es certain restrictions. For
instance, f x should be integrable in some ®nite region. In pra ctice, this means
that f x has, at worst, jump discontinuities or mild in®nite discontinuities. Also,
the integral should converge at in®nity. This would require that f x!0as
x !1.
A very common sucient condition is the requirement that f x is absolutely
integrable. That is, the integral
Z
1
ÿ1
f x
jj
dx
exists. Since jf xe
ÿi!x
jjf xj, it follows that the integral for g! is absolut ely
convergent; therefore it is convergent.
It is obvious that g! is, in general, a complex function of the real variable !.
So if f x is real, then
gÿ!g*!:
There are two immediate corollaries to this property:
(1) f x is even, g! is real;
(2) if f x is odd, g! is purely imaginary.
Other, less symmetrical forms of the Fourier integral can be obtained by working
directly with the sine and cosine series, instead of with the exponential functions.
Example 4.7
Consider the Gaussian probability function f xNe
ÿx
2
, where N and are
constant. Find its Fourier transform g!, then graph f x and g!.
Solution: Its Fourier transform is given by
g!
1
2
p
Z
1
ÿ1
f xe
ÿi!x
dx
N
2
p
Z
1
ÿ1
e
ÿx
2
e
ÿi!x
dx:
This integral can be simpli®ed by a change of variable. First, we note that
ÿx
2
ÿ i!x ÿx
p
i!=2
p
2
ÿ !
2
=4;
and then make the change of variable x
p
i!=2
p
u to obtain
g!
N
2
p
e
ÿ!
2
=4
Z
1
ÿ1
e
ÿu
2
du
N
2
p
e
ÿ!
2
=4
:
167
FOURIER INTEGRALS AND FOURIER TRANSFORMS
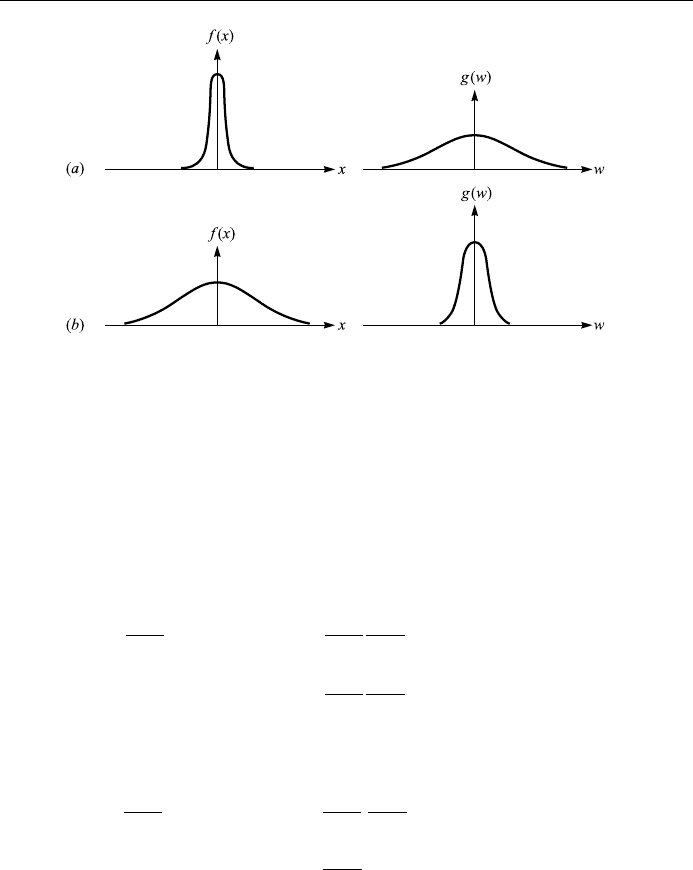
It is easy to see that g! is also a Gaussian probability function with a peak at the
origin, monotonically decreasing as ! !1. Furthermore, for large , f x is
sharply peaked but g! is ¯attened, and vice versa as shown in Fig. 4.13. It is
interesting to note that this is a general feat ure of Fourier transforms. We shall see
later that in quantum mechanical applications it is related to the Heisenberg
uncertainty principle.
The original fun ction f x can be retrieved from Eq. (4.31) which takes the
form
1
2
p
Z
1
ÿ1
g!e
i!x
d!
1
2
p
N
2
p
Z
1
ÿ1
e
ÿ!
2
=4
e
i!x
d!
1
2
p
N
2
p
Z
1
ÿ1
e
ÿ
0
!
2
e
ÿi!x
0
d!
in which we have set
0
1=4, and x
0
ÿx. The last integral can be evaluated
by the same technique, and we ®nally ®nd
1
2
p
Z
1
ÿ1
g!e
i!x
d!
1
2
p
N
2
p
Z
1
ÿ1
e
ÿ
0
!
2
e
ÿi!x
0
d!
N
2
p
2
p
e
ÿx
2
Ne
ÿx
2
f x:
Example 4.8
Given the box function which can represent a single pulse
f x
1 jxja
0 x
jj
> a
®nd the Fourier transform of f x, g!; then graph f x and g! for a 3.
168
FOURIER SERIES AND INTEGRALS
Figure 4.13. Gaussian probability function: a large ; b small .

Solution: The Fourier transform of f x is, as shown in Fig. 4.14,
g!
1
2
p
Z
1
ÿ1
f x
0
e
ÿi!x
0
dx
0
1
2
p
Z
a
ÿa
1e
ÿi!x
0
dx
0
1
2
p
e
ÿi!x
0
ÿi!
a
ÿa
þ
þ
þ
þ
þ
2
r
sin !a
!
;!6 0:
For ! 0, we obtain g!
2=
p
a.
The Fourier integral representation of f x is
f x
1
2
p
Z
1
ÿ1
g!e
i!x
d!
1
2
Z
1
ÿ1
2 sin !a
!
e
i!x
d!:
Now
Z
1
ÿ1
sin !a
!
e
i!x
d!
Z
1
ÿ1
sin !a cos !x
!
d! i
Z
1
ÿ1
sin !a sin !x
!
d!:
The integrand in the second integral is odd and so the integral is zero. Thus we
have
f x
1
2
p
Z
1
ÿ1
g!e
i!x
d!
1
Z
1
ÿ1
sin !a cos !x
!
d!
2
Z
1
0
sin !a cos !x
!
d!;
the last step follows since the integrand is an even function of !.
It is very dicult to evaluate the last integral. But a known property of f x will
help us. We know that f x is equal to 1 for jxja, and equ al to 0 for jxj > a.
Thus we can write
2
Z
1
0
sin !a cos !x
!
d!
1 jxja
0 jxj > a
169
FOURIER INTEGRALS AND FOURIER TRANSFORMS
Figure 4.14. The box function.

Just as in Fourier series expansion, we also expect to observe Gibb's
phenomenon in the case of Fourier integrals. Approximations to the Fourier
integral are obtained by replacing 1 by :
Z
0
sin ! cos !x
!
d!;
where we have set a 1. Fig. 4.15 shows oscillations near the points of disconti-
nuity of f x. We might expect these oscillations to disappear as !1, but they
are just shifted closer to the points x 1.
Example 4.9
Consider now a harmonic wave of frequency !
0
, e
i!
0
t
, which is chopped to a life-
time of 2T seconds (Fig. 4.16(a)):
f t
e
i!
0
t
ÿT t T
0 jtj > 0
:
(
The chopping process will introduce many new frequencies in varying amounts,
given by the Fourier transform. Then we have, according to Eq. (4.30),
g!2
ÿ1=2
Z
T
ÿT
e
i!
0
t
e
ÿi!t
dt 2
ÿ1=2
Z
T
ÿT
e
i!
0
ÿ!t
dt
2
ÿ1=2
e
i!
0
ÿ!t
i!
0
ÿ !
þ
þ
þ
þ
T
ÿT
2=
1=2
T
sin!
0
ÿ !T
!
0
ÿ !T
:
This function is plotted schematically in Fig. 4.16(b). (Note that
lim
x!0
sin x=x1.) The most striking aspect of this graph is that, although
the principal contribution comes from the frequencies in the neighborhood of
!
0
, an in®nite number of frequencies are presented. Nature provides an example
of this kind of chopping in the emission of photons during electronic and nuclear
transitions in atoms. The light emitted from an atom con sists of regular vibrations
that last for a ®nite time of the order of 10
ÿ9
s or longer. When light is examined
by a spectroscope (which measures the wavelengths and, hence, the frequencies)
we ®nd that there is an irreducible minimum frequency spread for each spectrum
line. This is known as the natural line width of the radiation.
The relative percentage of frequencies, other than the basic one, present
depends on the shape of the pulse, and the spread of frequencies depends on
170
FOURIER SERIES AND INTEGRALS
Figure 4.15. The Gibb's phenomenon.

the time T of the duration of the pulse. As T becomes larger the central peak
becomes higher and the width ! 2=T becomes smaller. Considering only
the spread of frequencies in the central peak we have
! 2=T; or T 1:
Multiplying by the Planck constant h and replacing T by t, we have the relation
tE h: 4:32
A wave train that lasts a ®nite time also has a ®nite extension in space. Thus the
radiation emitted by an atom in 10
ÿ9
s has an extension equal to 3 10
8
10
ÿ9
3 10
ÿ1
m. A Fourier analysis of this pulse in the space domain will yield a graph
identical to Fig. 4.11(b), with the wave numbers clustered around
k
0
2=
0
!
0
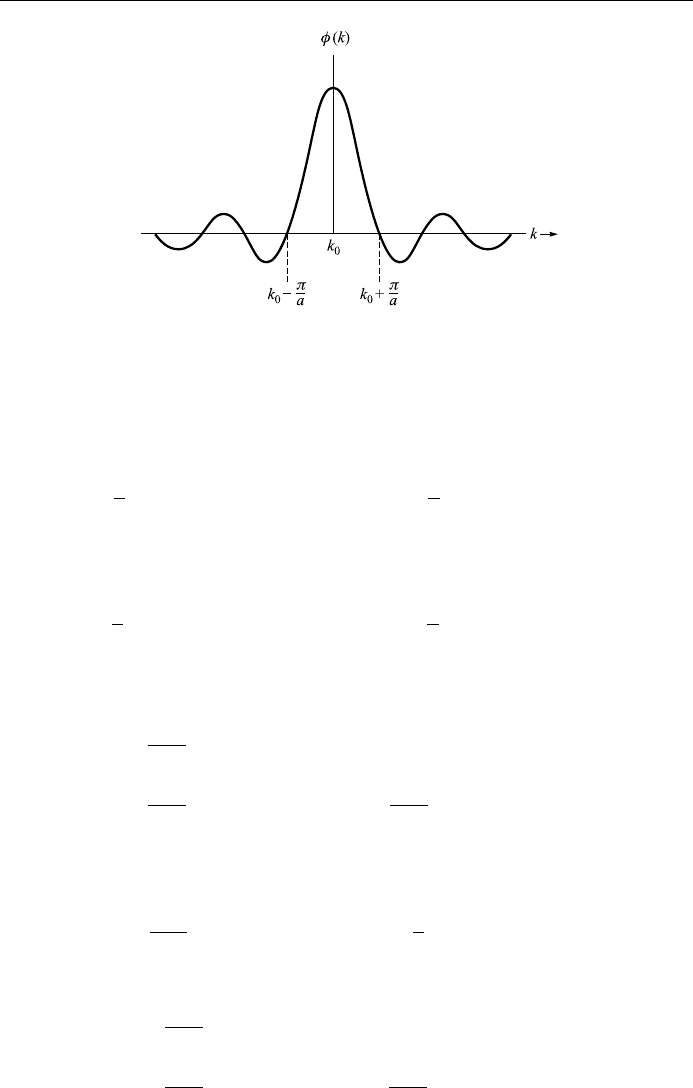
=v. If the wave train is of length 2a, the spread in wave number
will be given by a k 2, as shown below. This time we are chopping an in®nite
plane wave front with a shutter such that the length of the packet is 2a, where
2a 2vT, and 2T is the time interval that the shutter is open. Thus
ýx
e
ik
0
x
; ÿa x a
0; jxj > a
:
(
Then
k2
ÿ1=2
Z
1
ÿ1
ýxe
ÿikx
dx 2
ÿ1=2
Z
a
ÿa
ýxe
ÿikx
dx
2=
1=2
a
sink
0
ÿ ka
k
0
ÿ ka
:
This function is plotted in Fig. 4.17: it is identical to Fig. 4.16(b), but here it is the
wave vector (or the momentum) that takes on a spread of values around k
0
. The
breadth of the centra l peak is k 2=a,orak 2.
171
FOURIER INTEGRALS AND FOURIER TRANSFORMS
Figure 4.16. (a) A chopped harmonic wave e
i!
0
t
that lasts a ®nite time 2T. b
Fourier transform of e
i!
0
t
; jtj < T , and 0 otherwise.
Fourier sine and cosine transforms
If f x is an odd function, the Fourier transforms reduce to
g!
2
r
Z
1
0
f x
0
sin !x
0
dx
0
; f x
2
r
Z
1
0
g!sin !xd!: 4:33a
Similarly, if f x is an even function, then we have Fourier cosine transforma-
tions:
g!
2
r
Z
1
0
f x
0
cos !x
0
dx
0
; f x
2
r
Z
1
0
g!cos !xd!: 4 :33b
To demonstrate these results, we ®rst expand the exponential function on the
right hand side of Eq. (4.30)
g!
1
2
p
Z
1
ÿ1
f x
0
e
ÿi!x
0
dx
0
1
2
p
Z
1
ÿ1
f x
0
cos !x
0
dx
0
ÿ
i
2
p
Z
1
ÿ1
f x
0
sin !x
0
dx
0
:
If f x is even, then f xcos !x is even and f xsin !x is odd. Thus the second
integral on the right hand side of the last equation is zero and we have
g!
1
2
p
Z
1
ÿ1
f x
0
cos !x
0
dx
0
2
r
Z
1
0
f x
0
cos !x
0
dx
0
;
g! is an even function, since gÿ!g! . Next from Eq. (4.31) we have
f x
1
2
p
Z
1
ÿ1
g!e
i!x
d!
1
2
p
Z
1
ÿ1
g!cos !xd!
i
2
p
Z
1
ÿ1
g!sin !xd!:
172
FOURIER SERIES AND INTEGRALS
Figure 4.17. Fourier transform of e
ikx
; jxja:

Since g! is even, so g!sin !x is odd and the second integral on the right hand
side of the last equation is zero, and we have
f x
1
2
p
Z
1
ÿ1
g!cos !xd!
2
r
Z
1
0
g!cos !xd!:
Similarly, we can prove Fourier sine transforms by replacing the cosine by the
sine.
Heisenberg's uncertainty principle
We have demonstrated in above examples that if f x is sharply peaked, then g!
is ¯attened, and vice versa. This is a general feature in the theory of Fourier
transforms and has important consequences for all instances of wave propaga-
tion. In electronics we understand now why we use a wide-band ampli®cation in
order to reproduce a sharp pulse without distortion.
In quantum mechanical applications this general feature of the theory of
Fourier transforms is related to the Heisenberg uncertainty principle. We saw
in Example 4.9 that the spread of the Fourier transform in k space (k) times
its spread in coordinate space (a) is equal to 2 ak 2. This result is of
special importance because of the connection between values of k and momentum
p: p pk (where p is the Planck constant h divide d by 2). A particle localized in
space must be represented by a superposition of waves with diÿerent momenta.
As a result, the position and moment um of a particle cannot be measured simul-
taneously with in®nite precision; the product of `uncertainty in the position deter-
mination' and `uncertainty in the momentum determination' is governed by the
relation xp h apk 2p h,orxp h; x a. This statement is
called Heisenberg's uncertainty principle. If position is known better, knowledge
of the momentum must be unavoidably reduced proportionally, and vice versa. A
complete knowledge of one, say k (and so p), is possible only when there is
complete ignorance of the other. We can see this in physical terms. A wave
with a unique value of k is in®nitely long. A particle represented by an in®nitely
long wave (a free particle) cannot have a de®nite position, since the particle can be
anywhere along its length. Hence the position uncertainty is in®nite in order that
the uncerta inty in k is zero.
Equation (4.32) represents Heisenberg's uncertainty principle in a diÿerent
form. It states that we cannot know with in®nite precision the exact energy of a
quantum system at every moment in time. In order to measure the energy of a
quantum system with good accuracy, one must carry out such a measurement for
a suciently long time. In other words, if the dynamical state exists only for a
time of order t, then the energy of the state cannot be de®ned to a precision
better than h=t.
173
HEISENBERG'S UNCERTAINTY PRINCIPLE

We should not look upon the uncerta inty principle as being merely an unfor-
tunate limitation on our ability to know nature with in®nite precision. We can use
it to our advantage. For example, when combining the time±energy uncertainty
relation with Einstein's mass±energy relation (E mc
2
) we obtain the relation
mt h=c
2
. This result is very useful in our quest to understand the universe, in
particular, the origin of matter.
Wave packets and group velocity
Energy (that is, a signal or information) is transmitted by groups of waves, not a
single wave. Phase velocity may be greater than the speed of light c, `group
velocity' is a lways less than c. The wave groups with which energy is transmitted
from place to place are called wave packets. Let us ®rst consider a simple case
where we have two waves '
1
and '
2
: each has the same amplitude but diÿers
slightly in frequency and wavelength,
'
1
x; tA cos!t ÿ kx;
'
2
x; tA cos! !t ÿk kx;
where ! ! and k k. Each represents a pure sinusoidal wave extending to
in®nite along the x-axis. Together they give a resultant wave
' '
1
'
2
A cos!t ÿ kxcos! !t ÿk kx
fg
:
Using the trigonometrical identity
cos A cos B 2 cos
A B
2
cos
A ÿ B
2
;
we can rewrite ' as
' 2 cos
2!t ÿ 2kx !t ÿ kx
2
cos
ÿ!t kx
2
2 cos
1
2
!t ÿ kxcos!t ÿ kx:
This represents an oscillation of the original frequency !, but with a modulated
amplitude as shown in Fig. 4.18. A given segment of the wave system, such as AB,
can be regarded as a `wave packet' and moves with a velocity v
g
(not yet deter-
mined). This segment contains a large number of oscil lations of the primary wave
that moves with the velocity v. And the velocity v
g
with which the modulated
amplitude propagates is called the group velocity and can be determined by the
requirement that the phase of the modulated amplitude be constant. Thus
v
g
dx=dt !=k ! d!=dk:
174
FOURIER SERIES AND INTEGRALS

The modulation of the wave is repeated ind e®nitely in the case of superposition of
two almost equal waves. We now use the Fourier technique to demonstrate that
any isolated packet of oscillatory disturbance of frequency ! can be described in
terms of a combination of in®nite trains of frequencies distributed around !. Let
us ®rst superpose a system of n waves
ýx; t
X
n
j1
A
j
e
ik
j
xÿ!
j
t
;
where A
j
denotes the amplitudes of the individual waves. As n approaches in®nity,
the frequencies become continuously distributed. Thus we can replace the sum-
mation with an integration, and obtain
ýx; t
Z
1
ÿ1
Ake
ikxÿ!t
dk; 4:34
the amplitude A k is often called the distribution function of the wave. For
ýx; t to represent a wave packet traveling with a characteristic group velocity,
it is necessary that the range of propagation vectors included in the superposition
be fairly small. Thus, we assume that the amplitude Ak60 only for a small
range of values about a particular k
0
of k:
Ak60; k
0
ÿ "<k < k
0
"; " k
0
:
The behavior in time of the wave packet is determined by the way in which the
angular frequency ! de pends upon the wave number k: ! !k, known as the
law of dispersion. If ! varies slowly wi th k, then !k can be expanded in a power
series about k
0
:
!k!k
0
d!
dk
þ
þ
þ
þ
0
k ÿ k
0
!
0
!
0
k ÿ k
0
O k ÿ k
0
2
hi
;
where
!
0
!k
0
; and !
0
d!
dk
þ
þ
þ
þ
0
175
WAVE PACKETS AND GROUP VELOCITY
Figure 4.18. Superposition of two waves.
