Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


distance between any particle pair constant at all times. Then its angular momen-
tum about the origin O of the coordinate system is
L
X
m
r
v
X
m
r
x r
where the subscript refers to mass m
a
located at r
x
1
; x
2
; x
3
, and x the
angular velocity of the rigid body.
Expanding the vector triple product by using the vector identity
A B CBA CÿCA B;
we obtain
L
X
m
br
2
x ÿ r
r
xc:
In terms of the components of the vectors r
and x, the ith component of L
i
is
L
i
X
m
!
i
X
3
k1
x
2
;k
ÿ x
;i
X
3
j1
x
; j
!
j
"#
X
j
!
j
X
m
ij
X
k
x
2
;k
ÿ x
;i
x
;j
"#
X
j
I
ij
!
j
or
~
L
~
I
~
!:
Both
~
L and
~
! are three-dimens ional column vectors, while
~
I is a 3 3 matrix and
is called the moment inertia matrix.
In general, the angular momentum vector L of a rigi d body is not always
parallel to its angular velocity x and
~
I is not a diagonal matrix. But we can orient
the coordinate axes in space so that all the non-diagonal elements I
ij
i 6 j
vanish. Such special directions are called the principal axes of inertia. If the
angular velocity is along one of these principal axes, the angular momentum
and the angular veloci ty will be parallel.
In many simple cases, especially when symmetry is present, the principal axes of
inertia can be found by inspection.
Normal modes of vibrations
Another good illustrative example of the application of matrix methods in classi-
cal physics is the longitudinal vibrations of a classical model of a carbon dioxide
molecule that has the chemical structure O±C±O. In particular, it provides a good
example of the eigenvalues and eigenvectors of an asymmetric real matrix.
136
MATRIX ALGEBRA

We can regard a carbon dioxide molecule as equivalent to a set of three par-
ticles jointed by elastic springs (Fig. 3.5). Clearly the system wi ll vibrate in some
manner in response to an external force. For simplicity we shall consider only
longitudinal vibrations, and the interactions of the oxygen molecules with one
another will be neglected, so we consider only nearest neighbor interaction. The
Lagrangian function L for the system is
L
1
2
m
_
x
2
1
_
x
2
3
1
2
M
_
x
2
2
ÿ
1
2
kx
2
ÿ x
1
2
ÿ
1
2
kx
3
ÿ x
2
2
;
substituting this into Lagrange's equations
d
dt
@L
@
_
x
i
ÿ
@L
@x
i
0 i 1; 2; 3;
we ®nd the equations of motion to be
x
1
ÿ
k
m
x
1
ÿ x
2
ÿ
k
m
x
1
k
m
x
2
;
x
2
ÿ
k
M
x
2
ÿ x
1
ÿ
k
M
x
2
ÿ x
3
k
M
x
1
ÿ
2k
M
x
2
k
M
x
3
;
x
3
k
m
x
2
ÿ
k
m
x
3
;
where the dots denote time derivatives. If we de®n e
~
X
x
1
x
2
x
3
0
B
@
1
C
A
;
~
A
ÿ
k
m
k
m
0
ÿ
k
M
ÿ
2k
M
k
M
0
k
m
ÿ
k
m
0
B
B
B
B
B
B
B
@
1
C
C
C
C
C
C
C
A
and, furthermore, if we de®ne the derivative of a matrix to be the matrix obtained
by diÿerentiating each matrix element, then the above system of diÿerential equa-
tions can be writt en as
~
X
~
A
~
X:
137
NORMAL MODES OF VIBRATIONS
Figure 3.5. A linear symmetrical carbon dioxide molecule.
This matrix equation is reminiscent of the single diÿerential equation
x ax, with
a a constant. The latter always has an exponential solution. This suggests that we
try
~
X
~
Ce
!t
;
where ! is to be determined and
~
C
C
1
C
2
C
3
0
B
@
1
C
A
is an as yet unknown constant matrix. Substituting this into the above matrix
equation, we obtain a matrix-eigenvalue equation
~
A
~
C !
2
~
C
or
ÿ
k
m
k
m
0
ÿ
k
M
ÿ
2k
M
k
M
0
k
m
ÿ
k
m
0
B
B
B
B
B
B
B
B
B
@
1
C
C
C
C
C
C
C
C
C
A
C
1
C
2
C
3
0
B
@
1
C
A
!
2
C
1
C
2
C
3
0
B
@
1
C
A
: 3:77
Thus the possible values of ! are the square roots of the eigenvalues of the
asymmetric matrix
~
A with the corresponding solutions being the eigenvectors of
the matrix
~
A. The secular equation is
ÿ
k
m
ÿ !
2
k
m
0
ÿ
k
M
ÿ
2k
M
ÿ !
2
k
M
0
k
m
ÿ
k
m
ÿ !
2
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
þ
0:
This leads to
!
2
ÿ!
2
k
m
ÿ!
2
k
m
2k
M
0:
The eigenvalues are
!
2
0;
k
m
; and
k
m
2k
M
;
138
MATRIX ALGEBRA
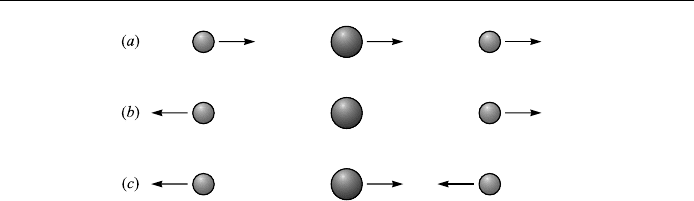
all real. The correspondi ng eigenvectors are determined by substituting the eigen-
values back into Eq. (3.77) one eigenvalue at a time:
(1) Setting !
2
0 in Eq. (3.77) we ®nd that C
1
C
2
C
3
. Thus this mode is
not an oscillation at all, but is a pure translation of the system as a whole, no
relative motion of the masses (Fig. 3.6(a)).
(2) Setting !
2
k=m in Eq. (3.77), we ®nd C
2
0 and C
3
ÿC
1
. Thus the
center mass M is stationary while the outer masses vibrate in opposite
directions with the same amplitude (Fig. 3.6(b)).
(3) Setting !
2
k=m 2k=M in Eq. (3.77), we ®nd C
1
C
3
, and
C
2
ÿ2C
1
m=M. In this mode the two outer masses vibrate in
unison and the center mass vibrates oppositely with diÿerent amplitude
(Fig. 3.6(c)).
Direct product of mat rices
Sometimes the direct product of matrices is useful. Given an m m matrix
~
A
and an n n matrix
~
B, the direct product of
~
A and
~
B is an mn mn matrix,
de®ned by
~
C
~
A þ
~
B
a
11
~
Ba
12
~
B a
1m
~
B
a
21
~
Ba
22
~
B a
2m
~
B
.
.
.
.
.
.
.
.
.
a
m1
~
Ba
m2
~
B a
mm
~
B
0
B
B
B
B
B
@
1
C
C
C
C
C
A
:
For example, if
~
A
a
11
a
12
a
21
a
22
ý!
;
~
B
b
11
b
12
b
21
b
22
ý!
;
then
139
DIRECT PRODUCT OF MATRICES
Figure 3.6. Longitudinal vibrations of a carbon dioxide molecule.

~
A þ
~
B
a
11
~
Ba
12
~
B
a
21
~
Ba
22
~
B
ý!
a
11
b
11
a
11
b
12
a
12
b
11
a
12
b
12
a
11
b
21
a
11
b
22
a
12
b
21
a
12
b
22
a
21
b
11
a
21
b
12
a
22
b
11
a
22
b
12
a
21
b
21
a
21
b
22
a
22
b
21
a
22
b
22
0
B
B
B
B
@
1
C
C
C
C
A
:
Problems
3.1 For the pairs
~
A and
~
B given below, ®nd
~
A
~
B,
~
A
~
B,and
~
A
2
:
~
A
12
34
;
~
B
56
78
:
3.2 Show that an n-rowed diagonal matrix
~
D
~
D
k 0 0
0 k 0
.
.
.
.
.
.
.
.
.
k
0
B
B
B
B
@
1
C
C
C
C
A
commutes with any n-rowed square matrix
~
A:
~
A
~
D
~
D
~
A k
~
A.
3.3 If
~
A,
~
B,and
~
C are any matrices such that the addition
~
B
~
C and the
products
~
A
~
B and
~
A
~
C are de®ned, show that
~
A(
~
B
~
C
~
A
~
B +
~
A
~
C. That
is, that matrix multiplication is distributive.
3.4 Given
~
A
010
101
010
0
B
@
1
C
A
;
~
B
100
010
001
0
B
@
1
C
A
;
~
C
10 0
00 0
00ÿ1
0
B
@
1
C
A
;
show that [
~
A;
~
B0, and [
~
B;
~
C0, but that
~
A does not commute with
~
C.
3.5 Prove that (
~
A
~
B
T
~
A
T
~
B
T
.
3.6 Given
~
A
2 ÿ3
04
;
~
B
ÿ52
21
; and
~
C
01ÿ2
30 4
:
(a) Find 2
~
A ÿ 4
~
B,2(
~
A ÿ 2
~
B)
(b) Find
~
A
T
;
~
B
T
;
~
B
T
T
(c) Find
~
C
T
;
~
C
T
T
(d)Is
~
A
~
C de®ned?
(e)Is
~
C
~
C
T
de®ned?
( f )Is
~
A
~
A
T
symmetric?
140
MATRIX ALGEBRA

(g)Is
~
A ÿ
~
A
T
antisymmetric?
3.7 Show that the matrix
~
A
140
250
360
0
B
@
1
C
A
is not invertible.
3.8 Show that if
~
A and
~
B are invertible matrices of the same order, then
~
A
~
B is
invertible.
3.9 Given
~
A
123
253
108
0
B
@
1
C
A
;
®nd
~
A
ÿ1
and check the answer by direct multiplication.
3.10 Prove that if
~
A is a non-singular matrix, then det(
~
A
ÿ1
1= det
~
A).
3.11 If
~
A is an invertible n n matrix, show that
~
AX 0 has only the trivial
solution.
3.12 Show, by computing a matrix inverse, that the solution to the following
system is x
1
4, x
2
1:
x
1
ÿ x
2
3;
x
1
x
2
5:
3.13 Solve the system
~
AX
~
B if
~
A
100
020
001
0
B
@
1
C
A
;
~
B
1
2
3
0
B
@
1
C
A
:
3.14 Given matrix
~
A, ®nd A*, A
T
, and A
y
, where
~
A
2 3i 1 ÿ i 5i ÿ3
1 i 6 ÿ i 1 3i ÿ1 ÿ 2i
5 ÿ 6i 30 ÿ4
0
B
@
1
C
A
:
3.15 Show that:
(a) The matrix
~
A
~
A
y
, where
~
A is any matrix, is hermitian .
(b)
~
A
~
B
y
~
B
y
~
A
y
:
(c)If
~
A;
~
B are hermitian, then
~
A
~
B
~
B
~
A is hermitian.
(d)If
~
A and
~
B are hermitian, then i
~
A
~
B ÿ
~
B
~
A is hermitian.
3.16 Obtain the most general orthogonal matrix of order 2.
[Hint: use relations (3.34a) and (3.34b).]
3.17. Obtain the most general unitary matrix of order 2.
141
PROBLEMS

3.18 If
~
A
~
B 0, show that one of these matrices must have zero determinant .
3.19 Given the Pauli spin matrices (which are very important in quantum
mechanics)
1
01
10
;
2
0 ÿi
i 0
;
3
10
0 ÿ1
;
(note that the subscripts x; y, and z are sometimes used instead of 1, 2, and
3). Show that
(a) they are hermitian,
(b)
2
i
~
I; i 1; 2; 3
(c) as a result of (a) and (b) they are also unitary, and
(d)[
1
;
2
2I
3
et cycl.
Find the inverses of
1
;
2
;
3
:
3.20 Use a rotation matrix to show that
sin
1
2
sin
1
cos
2
sin
2
cos
1
:
3.21 Show that: Tr
~
A
~
B Tr
~
B
~
A and Tr
~
A
~
B
~
C Tr
~
B
~
C
~
A Tr
~
C
~
A
~
B:
3.22 Show that: (a) the trace and (b) the commutation relation between two
matrices are invariant under similarity transformations.
3.23 Determine the eigenvalues and eigenvectors of the matrix
~
A
ab
ÿba
:
Given
~
A
57ÿ5
04ÿ1
28ÿ3
0
B
@
1
C
A
;
®nd a matrix
~
S that diagonalizes
~
A, and show that
~
S
ÿ1
~
A
~
S is diagonal.
3.25 If
~
A and
~
B are square matrices of the same order, then
det(
~
A
~
Bdet
~
Adet
~
B: Verify this theorem if
~
A
2 ÿ1
32
;
~
B
72
ÿ34
:
3.26 Find a common set of eigenvectors for the two matrices
~
A
ÿ1
6
p
2
p
6
p
0
3
p
2
p
3
p
ÿ2
0
B
@
1
C
A
;
~
B
10
6
p
ÿ
2
p
6
p
9
3
p
ÿ
2
p
3
p
11
0
B
@
1
C
A
:
3.27 Show that two hermitian matrices can be made diagonal if and only if they
commute.
142
MATRIX ALGEBRA

3.28 Show the validity of the Cayley±Hamilton theorem by applying it to the
matrix
~
A
54
12
;
then use the Cayley±Hamilton theorem to ®nd the inverse of the matrix
~
A.
3.29 Given
~
A
01
10
;
~
B
0 ÿi
i 0
;
®nd the direct product of these matrices, and show that it does not com-
mute.
143
PROBLEMS
4
Fourier series and integrals
Fourier series are in®nite series of sines and cosines which are capable of repre-
senting almost any periodic function whether continuous or not. Periodic func-
tions that occur in physics and engineering problems are often very complicated
and it is desirable to represent them in terms of simple periodic functions.
Therefore the study of Fourier series is a matter of great practical importance
for physicists and engineers.
The ®rst part of this chapter deals with Fourier series. Basic concepts, facts, and
techniques in connection with Fourier series will be introduced and developed,
along with illustrative examples. They are followed by Fourier integrals and
Fourier transforms.
Periodic functions
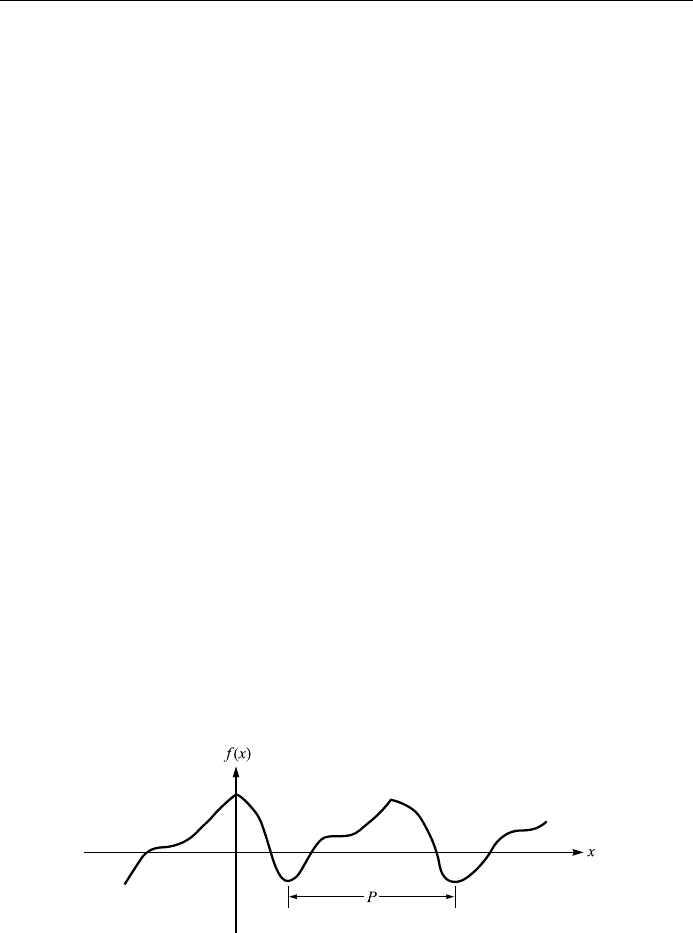
If function f x is de®ned for all x and there is some positive constant P such that
f x Pf x4:1
then we say that f x is periodic with a period P (Fig. 4.1). From Eq. (4.1) we also
144
Figure 4.1. A general periodic function.
have, for all x and any integer n,
f x nPf x:
That is, every periodic function has arbitrarily large periods and contains arbi-
trarily large numbers in its domain. We call P the fundamental (or least) period,
or simply the period.
A periodic function need not be de®ned for all values of its independent vari-
able. For example, tan x is unde®ned for the values x =2 n. But tan x is a
periodic function in its domain of de®nition, with as its fundamental period:
tan(x tan x.
Example 4.1
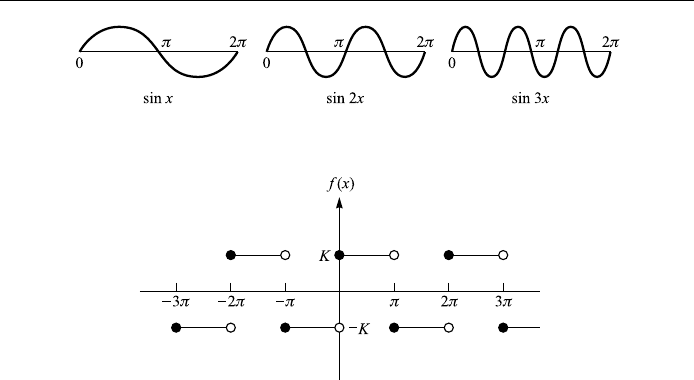
(a) The period of sin x is 2, since sin(x 2 , sin(x 4; sinx 6; ... are all
equal to sin x, but 2 is the least value of P. And, as shown in Fig. 4.2, the period
of sin nx is 2=n, where n is a positive integer.
(b) A constant function has any positive number as a period. Since f x
c (const.) is de®ned for all real x, then, for every positive number P,
f x Pc f x. Hence P is a period of f. Furthermore, f has no fundamental
period.
(c)
f x
K for 2nx 2n 1
ÿK for 2n 1 x < 2n 2
(
n 0; 1; 2; 3; ...
is periodic of period 2 (Fig. 4.3).
145
PERIODIC FUNCTIONS
Figure 4.2. Sine functions.
Figure 4.3. A square wave function.
