Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


and the subscript zero means `evaluated' at k k
0
. Now the argument of the
exponential in Eq. (4.34) can be rewritten as
!t ÿ kx !
0
t ÿ k
0
x!
0
k ÿ k
0
t ÿk ÿ k
0
x
!
0
t ÿ k
0
xk ÿ k
0
!
0
t ÿ x
and Eq. (4.34) becomes
ýx; texpik
0
x ÿ !
0
t
Z
k
0
"
k
0
ÿ"
Akexpik ÿ k
0
x ÿ !
0
tdk: 4:35
If we take k ÿ k
0
as the new integration variable y and assume Ak to be a slowly
varying function of k in the integration interval 2", then Eq. (4.35) becomes
ýx; texpik
0
x ÿ !
0
t
Z
k
0
"
k
0
ÿ"
Ak
0
yexpix ÿ !
0
tydy:
Integration, transformation, and the approximation Ak
0
yAk
0
lead to
the result
ýx; tBx; texpik
0
x ÿ !
0
t 4:36
with
Bx; t2Ak
0
sinkx ÿ !
0
t
x ÿ !
0
t
: 4:37
As the argument of the sine contains the small quantity k; B x; t varies slowly
depending on time t and coordinate x. Therefore, we can regard Bx; t as the
small amplitude of an approximately monochromatic wave and k
0
x ÿ !
0
t as its
phase. If we multiply the numerat or and denominator on the right hand side of
Eq. (4.37) by k and let
z kx ÿ !
0
t
then Bx; t becomes
Bx; t2Ak
0
k
sin z
z
and we see that the varia tion in amplitude is determined by the factor sin (z=z.
This has the properties
lim
z!0
sin z
z
1 for z 0
and
sin z
z
0 for z ; 2; ...:
176
FOURIER SERIES AND INTEGRALS

If we further increase the absolute value of z, the function sin (z=z runs alter-
nately through maxima and minima, the function values of which are small com-
pared with the principal maximum at z 0, and quickly converges to zero.
Therefore, we can conclude that superposition generates a wave packet whose
amplitude is non-zero only in a ®nite region, and is described by sin (z=z (see Fig.
4.19).
The modulating factor sin (z=z of the amplitude assumes the maximum value 1
as z ! 0. Recall that z kx ÿ !
0
t), thus for z 0, we have
x ÿ !
0
t 0;
which means that the maximum of the amplitude is a plane propagating with
velocity
dx
dt
!
0
d!
dk
þ
þ
þ
þ
0
;
that is, !
0
is the group velocity, the velocity of the whole wave packet.
The concept of a wave packet also plays an important role in quantum
mechanics. The idea of associating a wave-like property with the electron and
other material particles was ®rst proposed by Louis Victor de Broglie (1892±1987)
in 1925. His work was motivated by the mystery of the Bohr orbits. After
Rutherford's successful -particle scattering experiments, a planetary-type
nuclear atom, with electrons orbiting around the nucleus, was in favor with
most physicists. But, according to classical electromagnetic theory, a charge
undergoing continuous centripetal acceleration emits electromagnetic radiation
177
WAVE PACKETS AND GROUP VELOCITY
Figure 4.19. A wave packet.

continuously and so the electron would lose energy continuously and it would
spiral into the nucleus after just a fraction of a second. This does not occur.
Furthermore, atoms do not radiate unless excited, and when radiation does
occur its spectrum consists of discrete frequencies rather than the continuum of
frequencies predicted by the classical electromagnetic theory. In 1913 Niels Bohr
(1885±1962) proposed a theory which successfully explained the radiation spectra
of the hydrogen atom. According to Bohr's postulates, an atom can exist in
certain allowed stationary states without radiation. Only when an electron
makes a transition between two allowed stationary states, does it emit or absorb
radiation. The possible stationary states are those in which the angular momen-
tum of the electron about the nucleus is quantized, that is, mvr np, where v is
the speed of the electron in the nth orbit and r is its radius. Bohr didn't clearly
describe this quantum condition. De Broglie attempted to explai n it by ®tting a
standing wave around the circumference of each orbit. Thus de Broglie proposed
that n 2r, where is the wavelength associated with the nth orbit. Combining
this with Bohr's quantum condition we immediately obtain
h
mv
h
p
:
De Broglie proposed that any material parti cle of total energy E and momentum p
is accompanied by a wave whose wavelength is given by h=p and whose
frequency is given by the Planck formula E=h. Today we call these waves
de Broglie waves or matter waves. The physical nature of these matter waves was
not clearly described by de Broglie, we shall not ask what these matter waves are ±
this is addressed in most textbooks on quantum mechanics. Let us ask just one
question: what is the (phase) velocity of such a matter wave? If we denote this
velocity by u, then
u
E
p
1
p
p
2
c
2
m
2
0
c
4
q
c
1 m
0
c=p
2
q
c
2
v
p
m
0
v
1 ÿ v
2
=c
2
p
ý!
;
which shows that for a particle with m
0
> 0 the wave velocity u is always greater
than c, the speed of light in a vacuum. Instead of individual waves, de Broglie
suggested that we can think of particles inside a wave packet, synthes ized from a
number of individual waves of diÿerent frequencies, with the entire packet travel-
ing with the particle velocity v.
De Broglie's matter wave idea is one of the cornerstones of quantum
mechanics.
178
FOURIER SERIES AND INTEGRALS

Heat conduction
We now consider an application of Fourier integrals in classical physics. A semi-
in®nite thin bar (x 0), whose surface is insulated, has an initial temperature
equal to f x. The temperature of the end x 0 is suddenly dropped to and
maintained at zero. The problem is to ®nd the temperature Tx; t at any point
x at time t. First we have to set up the boundary value problem for heat conduc-
tion, and then seek the general solution that will give the temperature Tx; t at
any point x at time t.
Head conduction equation
To establish the equation for heat conduction in a conducting medium we need
®rst to ®nd the heat ¯ux (the amount of heat per unit area per unit time) across a
surface. Suppose we have a ¯at sheet of thickne ss n, which has temperature T on
one side and T T on the other side (Fig. 4.20). The heat ¯ux which ¯ows from
the side of high temperature to the side of low temperature is directly proportional
to the diÿerence in temperature T and inversely proportional to the thickness
n. That is, the heat ¯ux from I to II is equal to
ÿK
T
n
;
where K, the constant of proportionality, is called the thermal conductivity of the
conducting medium. The minus sign is due to the fact that if T > 0 the heat
actually ¯ows from II to I. In the limit of n ! 0, the heat ¯ux across from II to I
can be written
ÿK
@T
@n
ÿKrT:
The quantity @T=@n is called the gradient of T which in vector form is rT.
We are now ready to derive the equation for heat condu ction. Let V be an
arbitrary volume lying within the solid and bounded by surface S. The total
179
HEAT CONDUCTION
n
Figure 4.20. Heat ¯ux through a thin sheet.

amount of heat entering S per unit time is
ZZ
S
KrT
^
ndS;
where
^
n is an outward unit vector normal to element su rface area dS. Using the
divergence theorem, this can be written as
ZZ
S
KrT
^
ndS
ZZZ
V
r KrTdV: 4:38
Now the heat contained in V is given by
ZZZ
V
cTdV;
where c and are respectively the speci®c heat capacity and density of the solid.
Then the time rate of increase of heat is
@
@t
ZZZ
V
cTdV
ZZZ
V
c
@T
@t
dV: 4:39
Equating the right hand sides of Eqs. (4.38) and (4.39) yields
ZZZ
V
c
@T
@t
ÿr KrT
dV 0:
Since V is arbitrary, the integrand (assumed continuous) must be identically zero:
c
@T
@t
r KrT
or if K, c, are constants
@T
@t
krrT kr
2
T; 4:40
where k K=c . This is the required equation for heat conduction and was ®rst
developed by Four ier in 1822. For the semiin®nite thin bar, the boundary condi-
tions are
Tx; 0f x; T0; t0; jTx; tj < M; 4:41
where the last condition means that the temperature must be bounded for physical
reasons.
A solution of Eq. (4.40) can be obtaine d by separation of variables, that is by
letting
T XxHt:
Then
XH
0
kX
00
H or X
00
=X H
0
=kH:
180
FOURIER SERIES AND INTEGRALS

Each side must be a constant which we call ÿ
2
. (If we use
2
, the resulting
solution does not satisfy the boundedness condition for real values of .) Then
X
00
2
X 0; H
0
2
kH 0
with the solutions
XxA
1
cos x B
1
sin x; HtC
1
e
ÿk
2
t
:
A solution to Eq. (4.40) is thus given by
Tx; tC
1
e
ÿk
2
t
A
1
cos x B
1
sin x
e
ÿk
2
t
A cos x B sin x:
From the second of the bounda ry con ditions (4.41) we ®nd A 0 and so Tx; t
reduces to
Tx; tBe
ÿk
2
t
sin x:
Since there is no restriction on the value of , we can replace B by a function B
and integrate over from 0 to 1 and still have a solution:
Tx; t
Z
1
0
Be
ÿk
2
t
sin xd: 4:42
Using the ®rst of boundary conditions (4.41) we ®nd
f x
Z
1
0
Bsin xd:
Then by the Fourier sine transform we ®nd
B
2
Z
1
0
f xsin xdx
2
Z
1
0
f usin udu
and the temperature distribution along the semiin®nite thin bar is
Tx; t
2
Z
1
0
Z
1
0
f ue
ÿk
2
t
sin u sin xddu: 4:43
Using the relation
sin u sin x
1
2
cos u ÿ xÿcos u x;
Eq. (4.43) can be rewritten
Tx; t
1
Z
1
0
Z
1
0
f ue
ÿk
2
t
cos u ÿ xÿcos u xddu
1
Z
1
0
f u
Z
1
0
e
ÿk
2
t
cos u ÿ xd ÿ
Z
1
0
e
ÿk
2
t
cos u xd
du:
181
HEAT CONDUCTION
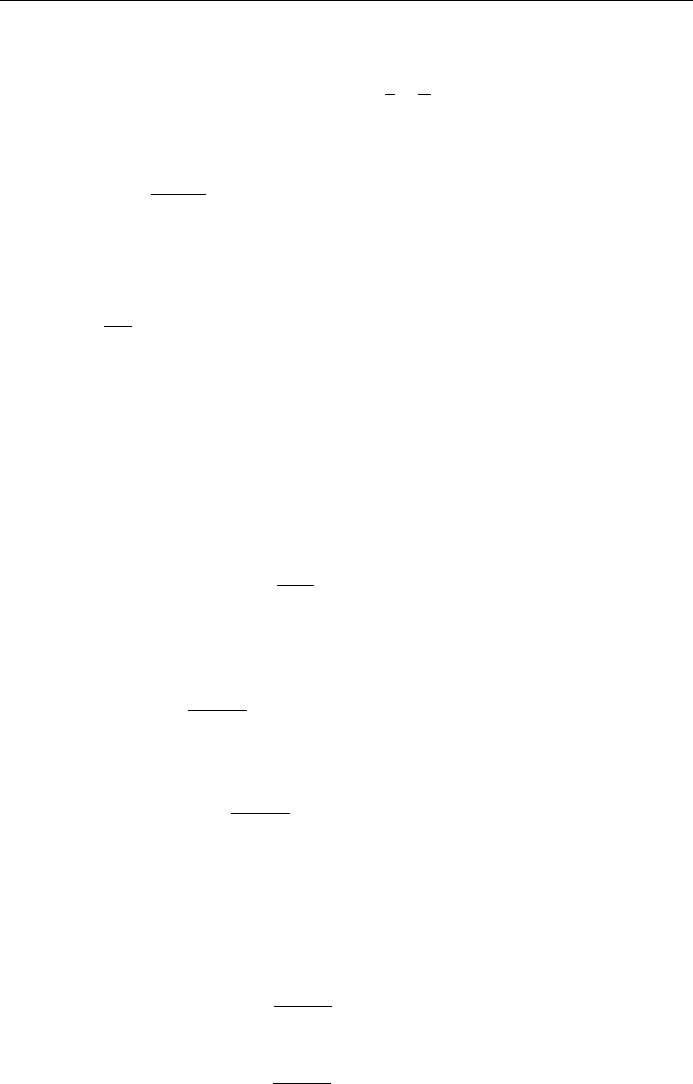
Using the integral
Z
1
0
e
ÿ
2
cos ÿd
1
2
r
e
ÿÿ
2
=4
;
we ®nd
Tx; t
1
2
kt
p
Z
1
0
f ue
ÿuÿx
2
=4kt
du ÿ
Z
1
0
f ue
ÿux
2
=4kt
du
:
Letting u ÿ x=2
kt
p
w in the ®rst integral and u x=2
kt
p
w in the second
integral, we obtain
Tx; t
1
p
Z
1
ÿx=2
kt
p
e
ÿw
2
f 2w
kt
p
xdw ÿ
Z
1
x=2
kt
p
e
ÿw
2
f 2w
kt
p
ÿ xdw
"#
:
Fourier transforms for functions of several variables
We can extend the development of Fourier transforms to a function of several
variables, such as f x; y; z. If we ®rst decompose the function into a Four ier
integral with respect to x, we obtain
f x; y; z
1
2
p
Z
1
ÿ1
þ!
x
; y; ze
i!
x
x
d!
x
;
where þ is the Fourier transform. Similarly, we can decompose the function with
respect to y and z to obtain
f x; y; z
1
2
2=3
Z
1
ÿ1
g!
x
;!
y
;!
z
e
i!
x
x!
y
y!
z
z
d!
x
d!
y
d!
z
;
with
g!
x
;!
y
;!
z
1
2
2=3
Z
1
ÿ1
f x; y; ze
ÿi!
x
x!
y
y!
z
z
dxdydz:
We can regard !
x
;!
y
;!
z
as the components of a vector ! whose magnitude is
!
!
2
x
!
2
y
!
2
z
q
;
then we express the above results in terms of the vector !:
f r
1
2
2=3
Z
1
ÿ1
gxe
ixr
dx; 4:44
gx
1
2
2=3
Z
1
ÿ1
f re
ÿixr
dr: 4:45
182
FOURIER SERIES AND INTEGRALS

The Fourier integral and the delta function
The delta function is a very useful tool in physics, but it is not a function in the
usual mathematical sense. The need for this strange `function' arises naturally
from the Fourier integrals. Let us go back to Eqs. (4.30) and (4.31) and substitute
g! into f x; we then have
f x
1
2
Z
1
ÿ1
d!
Z
1
ÿ1
dx
0
f x
0
e
i!xÿx
0
:
Interchanging the order of integration gives
f x
Z
1
ÿ1
dx
0
f x
0
1
2
Z
1
ÿ1
d!e
i!xÿx
0
: 4:46
If the above equation holds for any function f x, then this tells us something
remarkable about the integral
1
2
Z
1
ÿ1
d!e
i!xÿx
0
considered as a function of x
0
. It vanishes everywhere except at x
0
x, and its
integral with respect to x
0
over any interval including x is unity. That is, we may
think of this functi on as having an in®nitely high, in®nitely narrow peak at
x x
0
. Such a strange function is called Dirac's delta function (®rst introduced
by Paul A. M. Dirac):
x ÿ x
0
1
2
Z
1
ÿ1
d!e
i!xÿx
0
: 4:47
Equation (4.46) then becomes
f x
Z
1
ÿ1
f x
0
x ÿ x
0
dx
0
: 4:48
Equation (4.47) is an integral representation of the delta function. We summarize
its properties below:
x ÿ x
0
0; if x
0
6 x; 4:49a
Z
b
a
x ÿ x
0
dx
0
0; if x > b or x < a
1; if a < x < b
;
4:49b
f x
Z
1
ÿ1
f x
0
x ÿ x
0
dx
0
: 4:49c
183
THE FOURIER INTEGRAL AND THE DELTA FUNCTION

It is often convenient to place the origin at the singular point, in which case the
delta functi on may be written as
x
1
2
Z
1
ÿ1
d!e
i!x
: 4:50
To exami ne the behavior of the function for both small and large x, we use an
alternative representation of this function obtained by integrating as follows:
x
1
2
lim
a!1
Z
a
ÿa
e
i!x
d! lim
a!1
1
2
e
iax
ÿ e
ÿiax
ix
lim
a!1
sin ax
x
; 4:51
where a is positive and real. We see immediately that ÿxx. To examine
its behavior for small x, we consider the limit as x goes to zero:
lim
x!0
sin ax
x
a
lim
x!0
sin ax
ax
a
:
Thus, 0lim
a!1
a=!1, or the amplitude becomes in®nite at the singu-
larity. For large jxj, we see that sinax=x oscillates with period 2=a, and its
amplitude falls oÿ as 1=jxj. But in the limit as a goes to in®nity, the period
becomes in®nitesimally narrow so that the function approaches zero everywhere
except for the in®nite spike of in®nitesimal width at the singularity. What is the
integral of Eq. (4.5 1) over all space?
Z
1
ÿ1
lim
a!1
sin ax
x
dx lim
a!1
2
Z
1
0
sin ax
x
dx
2
2
1:
Thus, the delta function may be thought of as a spike function which has unit area
but a non-zero amplitude at the point of singularity, where the amplitude becomes
in®nite. No ordinary mathematical function with these properties exists. How do
we end up with such an improper function? It occurs because the change of order
of integration in Eq. (4.46) is not permi ssible. In spite of this, the Dirac delta
function is a most convenient function to use symbolically. For in applications the
delta function always occurs under an integral sign. Carrying out this integration,
using the formal properties of the delta function, is really equivalent to inverting
the order of integration once more, thus getting back to a mathematically correct
expression. Thus, using Eq. (4.49) we have
Z
1
ÿ1
f x x ÿ x
0
dx f x
0
;
but, on substituting Eq. (4.47) for the delta function, the integral on the left hand
side becomes
Z
1
ÿ1
f x
1
2
p
Z
1
ÿ1
d!e
i!xÿx
0
dx
184
FOURIER SERIES AND INTEGRALS

or, using the property ÿxx,
Z
1
ÿ1
f x
1
2
p
Z
1
ÿ1
d!e
ÿi!xÿx
0
dx
and changing the order of integration, we have
Z
1
ÿ1
f x
1
2
p
Z
1
ÿ1
d!e
ÿi!x
e
i!x
0
dx:
Comparing this expression with Eqs. (4.30) and (4.31), we see at once that this
double integ ral is equal to f x
0
, the correct mathe matical expression.
It is important to keep in mind that the delta function cannot be the end result of a
calculation and has meaning only so long as a subsequent integration over its argu-
ment is carried out.
We can easily verify the following most frequently required properties of the
delta function:
If a < b
Z
b
a
f x x ÿ x
0
dx
f x
0
; if a < x
0
< b
0; if x
0
< a or x
0
< b
; 4:52a
ÿxx; 4:52b
0
xÿ
0
ÿx;
0
xdx=dx; 4:52c
x x0; 4:52d
axa
ÿ1
x; a > 0; 4:52e
x
2
ÿ a
2
2a
ÿ1
x ÿ a x a; a > 0; 4:52f
Z
a ÿ xx ÿ bdx a ÿ b; 4:52g
f x x ÿ a f a x ÿ a: 4 :52h
Each of the ®rst six of these listed properties can be established by multiplying
both sides by a continuous, diÿerentiable function f x and then integrating over
x. For example, multiplying x
0
x by f x and integrating over x gives
Z
f xx
0
xdx ÿ
Z
x
d
dx
xf xdx
ÿ
Z
x f xxf
0
x
dx ÿ
Z
f x xdx:
Thus xx has the same eÿect when it is a factor in an integrand as has ÿx.
185
THE FOURIER INTEGRAL AND THE DELTA FUNCTION
