Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.

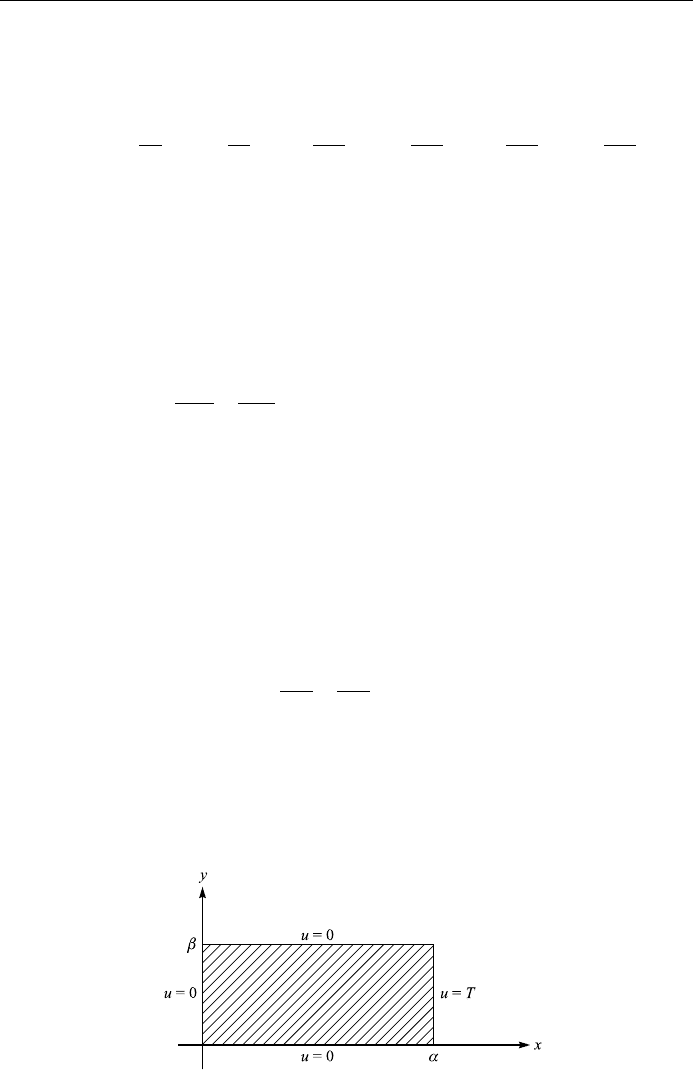
4.10 Find the exponential form of the Fourier series of the function whose de®-
nition in one period is f xe
ÿx
; ÿ1 < x < 1.
4.11 (a) Show that the set of functions
1; sin
x
L
; cos
x
L
; sin
2x
L
; cos
2x
L
; sin
3x
L
; cos
3x
L
; ...
form an orthogonal set in the interval ÿL; L.
(b) Determine the corresponding normalizing constants for the set in (a)so
that the set is orthonormal in ÿL; L.
4.12 Express f x; yxy as a Fourier series for 0 x 1; 0 y 2.
4.13 Steady-state heat conduction in a rectangular plate: Consider steady-state
heat conduction in a ¯at plate having temperature values prescribed on the
sides (Fig. 4.22). The boundary value problem modeling this is:
@
2
u
@
2
x
2
@
2
u
@
2
y
2
0; 0 < x <; 0 < y <ÿ;
ux; 0ux;ÿ0; 0 < x <;
u0; y0; u; yT; 0 < y <ÿ:
Determine the temperature at any point of the plate.
4.14 Derive and solve the following eigenvalue problem which occurs in the
theory of a vibrating square membrane whose sides, of length L, are kept
®xed:
@
2
w
@x
2
@
2
w
@y
2
w 0;
w0; ywL; y0 0 y L;
wx; 0wx; L0 0 y L:
196
FOURIER SERIES AND INTEGRALS
Figure 4.22. Flat plate with prescribed temperature.
4.15 Show that the Fourier integral can be written in the form
f x
1
Z
1
0
d!
Z
1
ÿ1
f x
0
cos !x ÿ x
0
dx
0
:
4.16 Starting with the form obtained in Problem 4.15, show that the Fourier
integral can be wri tten in the form
f x
Z
1
0
A!cos !x B!sin !x
fg
d!;
where
A!
1
Z
1
ÿ1
f xcos !xdx; B !
1
Z
1
ÿ1
f xsin !xdx:
4.17 (a) Find the Fourier transform of
f x
1 ÿ x
2
jxj < 1
0 jxj > 1
:
(
(b) Evaluate
Z
1
0
x cos x ÿ sin x
x
3
cos
x
2
dx:
4.18 (a) Find the Fourier cosine transform of f xe
ÿmx
; m > 0.
(b) Use the result in (a) to show that
Z
1
0
cos px
x
2
2
dx
2
e
ÿp
p > 0;>0 :
4.19 Solve the integral equation
Z
1
0
f xsin xdx
1 ÿ 0 1
0 >1
:
4.20 Find a bounde d solution to Laplace's equation r
2
ux; y0 for the half-
plane y > 0ifu takes on the value of f (x) on the x-axis:
@
2
u
@x
2
@
2
u
@y
2
0; ux; 0f x; ux; y
jj
< M:
4.21 Show that the following two functions are valid representations of the delta
function, where " is positive and real:
a x
1
p
lim
"!0
1
"
p
e
ÿx
2
="
b x
1
lim
"!0
"
x
2
"
2
:
197
PROBLEMS

4.22 Verify the following properties of the delta function:
(a) xÿx,
(b) xx0,
(c)
0
ÿxÿ
0
x,
(d) x
0
xÿx,
(e) ccxx; c > 0.
4.23 Solve the integral equation for yx
Z
1
ÿ1
yudu
x ÿ u
2
a
2
1
x
2
b
2
0 < a < b:
4.24 Use Fourier transforms to solve the boundary value problem
@u
@t
k
@
2
u
@x
2
; ux; 0f x; u x; t
jj
< M;
where ÿ1 < x < 1; t > 0.
4.25 Obtain a solution to the equation of a driven harmonic oscillator
xt2ÿ
_
xt!
2
0
xt0 Rt;
where ÿ and !
0
are positive and real constants.
198
FOURIER SERIES AND INTEGRALS

5
Linear vector spaces
Linear vector space is to quantum mechanics what calculus is to classical
mechanics. In this chapter the essential ideas of linear vector spaces will be dis-
cussed. The reader is already familiar with vector calculus in three-dimensional
Euclidean space E
3
(Chapter 1). We therefore present our discussion as a general -
ization of elementary vector calculus. The present ation will be, however, slightly
abstract and more form al than the discussion of vectors in Chapter 1. Any reader
who is not already familiar with this sort of discussion should be patient with the
®rst few sections. You will then be amply repaid by ®nding the rest of this chapter
relatively easy reading.
Euclidean n-space E
n
In the study of vector analysis in E
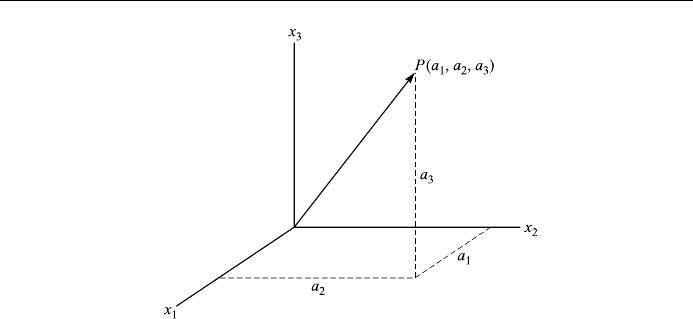
3
, an ordered triple of numbers (a
1
, a
2
, a
3
) has
two diÿerent geometric interpretations. It represents a point in space, with a
1
, a
2
,
a
3
being its coordinates; it also represents a vector, with a
1
, a
2
, and a
3
being its
components along the three coordinate axes (Fig. 5.1). This idea of using triples of
numbers to locate points in three-dimensional space was ®rst introduced in the
mid-seventeenth century. By the latter part of the nineteenth century physicists
and mathematicians began to use the quadruples of numbers ( a
1
, a
2
, a
3
, a
4
)as
points in four-dimensional space, quintuples (a
1
, a
2
, a
3
, a
4
, a
5
) as points in ®ve-
dimensional space etc. We now extend this to n-dimensional space E
n
, where n is a
positive integer. Although our geometric visualization doesn't extend beyond
three-dimensional space, we can extend many familiar ideas beyond three-dimen-
sional space by working with analytic or numerical properties of points and
vectors rather than their geometric properties.
For two- or three-dimensional space, we use the terms `ordered pair' and
`ordered triple.' When n > 3, we use the term `ordered-n-tuplet' for a sequence
199
of n numbers, real or complex, (a
1
, a
2
, a
3
; ...; a
n
); they will be viewed either as a
generalized point or a generalized vector in a n-dimensional space E
n
.
Two vectors u u
1
; u
2
; ...; u
n
and v v
1
; v
2
; ...; v
n
in E
n
are called equal if
u
i
v
i
; i 1; 2; ...; n 5:1
The sum u v is de®ned by
u v u
1
v
1
; u
2
v
2
; ...; u
n
v
n
5:2
and if k is any scalar, the scalar multiple ku is de®ned by
ku ku
1
; ku
2
; ...; ku
n
: 5:3
If u u
1
; u
2
; ...; u
n
is any vector in E
n
, its negative is given by
ÿu ÿu
1
; ÿu
2
; ...; ÿu
n
5:4
and the subtraction of vectors in E
n
can be considered as addition: v ÿ u
v ÿu. The null (zero) vector in E
n
is de® ned to be the vector 0 0; 0; ...; 0.
The addition and scalar multiplication of vectors in E
n
have the following
arithmetic properties:
u v v u; 5:5a
u v wu vw; 5:5b
u 0 0 u u; 5:5c
abuabu; 5:5d
au vau av; 5:5e
a bu au bu; 5:5f
where u, v, w are vectors in E
n
and a and b are scalars.
200
LINEAR VECTOR SPACES
Figure 5.1. A space point P whose position vector is A.

We usually de®ne the inner product of two vectors in E
3
in terms of lengths of
the vectors and the angle between the vectors: A B AB cos ; þA; B.We
do not de®ne the inner product in E
n
in the same manner. However, the inner
product in E
3
has a second equivalent expression in terms of comp onents:
A B A
1
B
1
A
2
B
2
A
3
B
3
. We choose to de®ne a similar formula for the gen-
eral case. We made this choice because of the further generalization that will be
outlined in the next section. Thus, for any two vectors u u
1
; u
2
; ...; u
n
and
v v
1
; v
2
; ...; v
n
in E
n
, the inner (or dot) product u v is de®ned by
u v u
1
*
v
1
u
2
*
v
2
u
n
*
v
n
5:6
where the asterisk denotes complex conjugation. u is often called the prefactor
and v the post-factor. The inner product is linear with respect to the post-factor,
and anti-linear with respect to the prefactor:
u av bwau v bu w; au bvw a*u vb*u w:
We expect the inner product for the general case also to have the following three
main features:
u v v u* 5:7a
u av bwau v bu w 5:7b
u u 0 0; if and only if u 0: 5:7c
Many of the familiar ideas from E
2
and E
3
have been carried over, so it is
common to refer to E
n
with the operations of addition, scalar multiplication, and
with the inner product that we have de®ned here as Euclidean n-space.
General linear vector spaces
We now generalize the concept of vector space still further: a set of `objects' (or
elements) obeying a set of axioms, which will be chosen by abstracting the most
important properties of vectors in E
n
, forms a linear vector space V
n
with the
objects called vectors. Before introducing the requisite axioms, we ®rst adapt a
notation for our general vectors: general vectors are designa ted by the symbol ji,
which we call, following Dirac, ket vectors; the conjugates of ket vectors are
denoted by the symbol hj, the bra vectors. However, for simplicity, we shall
refer in the future to the ket vectors jisimply as vectors, and to the hjsas
conjugate vectors. We now proceed to de®ne two basic operations on these
vectors: addition and multiplication by scalars.
By addition we mean a rule for forming the sum, denoted jý
1
ijý
2
i, for
any pair of vectors jý
1
i and jý
2
i.
By scalar multiplication we mean a rule for associating with each scalar k
and each vector jýi a new vector kjýi.
201
GENERAL LINEAR VECTOR SPACES

We now proceed to generalize the concept of a vector space. An arbitrary set of
n objects j1i; j2i; j3i; ...; ji; ...; j'i form a linear vector V
n
if these objects, called
vectors, meet the following axioms or properties:
A.1 If
ji
and '
ji
are objects in V
n
and k is a scalar, then
ji
'
ji
and k
ji
are
in V
n
, a feature called closure.
A.2
ji
'
ji
'
ji
ji
; that is, addition is commut ative.
A.3 (
ji
'
ji
ý
ji
ji
'
ji
ý
ji
); that is, addition is associative.
A.4 k
ji
'
ji
k
ji
k '
ji
; that is, scalar multiplication is distributive in the
vectors.
A.5 k
ji
k
ji
ji
; that is, scalar multiplication is distributive in the
scalars.
A.6 k
ji
k
ji
; that is, scalar multiplication is associative .
A.7 There exists a null vector 0
ji
in V
n
such that
ji
0
ji
ji
for all
ji
in V
n
.
A.8 For every vector
ji
in V
n
, there exists an inverse under addition, ÿ
ji
such
that
ji
ÿ
ji
0
ji
.
The set of numbers a; b; ... used in scalar multiplication of vectors is called the
®eld over which the vector ®eld is de®ned. If the ®eld consists of real numbers, we
have a real vector ®eld; if they are complex, we have a complex ®eld. Note that the
vectors themselves are neither real nor complex, the nature of the vectors is not
speci®ed. Vectors can be any kinds of objects; all that is required is that the vector
space axioms be satis®ed. Thus we purposely do not use the symbol V to denote
the vectors as the ®rst step to turn the reader away from the limited concept of the
vector as a directed line segment. Instead, we use Dirac's ket and bra symbols,
j
i
and j
h
, to denote generic vectors.
The familiar three-dimensional space of position vectors E
3
is an example of
a vector space over the ®eld of real numbers. Let us now examine two simple
examples.
Example 5.1
Let V be any plane through the origin in E
3
. We wish to show that the points in
the plane V form a vector space under the addition and scalar multiplication
operations for vector in E
3
.
Solution: Since E
3
itself is a vector space under the addition and scalar multi-
plication operations, thus Axioms A.2, A.3, A.4, A.5, and A.6 hold for all points
in E
3
and consequently for all points in the plane V. We therefore need only show
that Axioms A.1, A.7, and A.8 are satis®ed.
Now the plane V, passing through the origin, has an equation of the form
ax
1
bx
2
cx
3
0:
202
LINEAR VECTOR SPACES

Hence, if u u
1
; u
2
; u
3
and v v
1
; v
2
; v
3
are points in V, then we have
au
1
bu
2
cu
3
0andav
1
bv
2
cv
3
0:
Addition gives
au
1
v
1
bu
2
v
2
cu
3
v
3
0;
which shows that the point u v also lies in the plane V. This proves that Axiom
A.1 is satis®ed. Multiplying au
1
bu
2
cu
3
0 through by ÿ1 gives
aÿu
1
bÿu
2
cÿu
3
0;
that is, the point ÿu ÿu
1
; ÿu
2
; ÿu
3
lies in V. This establishes Axiom A.8.
The veri®cation of Axiom A.7 is left as an exercise.
Example 5.2
Let V be the set of all m n matrices with real elements. We know how to add
matrices and multiply matrices by scala rs. The corresponding rules obey closure,
associativity and distributive requirements. The null matrix has all zeros in it, and
the inverse under matrix addition is the matrix with all elements negated. Thus the
set of all m n matrices, together with the operations of matrix addition and
scalar multiplication, is a vector space. We shall denote this vector space by the
symbol M
mn
.
Subspaces
Consider a vector space V.IfW is a subset of V and form s a vector space under
the addition and scalar multiplication, then W is called a subspace of V. For
example, lines and planes passing through the origin form vector spaces and
they are subspaces of E
3
.
Example 5.3
We can show that the set of all 2 2 matrices having zero on the main diagonal is
a subspace of the vector space M
22
of all 2 2 matrices.
Solution: To prove this, let
~
X
0 x
12
x
21
0
ý!
~
Y
0 y
12
y
21
0
ý!
be two matrices in W and k any scalar. Then
k
~
X
0 x
12
kx
21
0
ý!
and
~
X
~
Y
0 x
12
y
12
x
21
y
21
0
ý!
and thus they lie in W. We leave the veri®cation of other axioms as exercises.
203
SUBSPACES

Linear combination
A vector W
ji
is a linear combination of the vectors v
1
ji
; v
2
ji
; ...; v
r
ji
if it can be
expressed in the form
W
ji
k
1
jv
1
ik
2
jv
2
ik
r
jv
r
i;
where k
1
; k
2
; ...; k
r
are scalars. For example, it is easy to show that the vector
W
ji
9; 2; 7 in E
3
is a linear combination of v
1
ji
1; 2; ÿ1 and
v
2
ji
6; 4; 2. To see this, let us write
9; 2; 7k
1
1; 2; ÿ1k
2
6; 4; 2
or
9; 2; 7k
1
6k
2
; 2k
1
4k
2
; ÿk
1
2k
2
:
Equating corresponding components gives
k
1
6k
2
9; 2k
1
4k
2
2; ÿk
1
2k
2
7:
Solving this system yields k
1
ÿ3 and k
2
2 so that
W
ji
ÿ3 v
1
ji
2 v
2
ji
:
Linear independence, bases, and dimensionality
Consider a set of vectors 1
ji
; 2
ji
; ...; r
ji
; ... n
ji
in a linear vector space V. If every
vector in V is expressible as a linear combination of 1
ji
; 2
ji
; ...; r
ji
; ...; n
ji
, then
we say that these vectors span the vector space V, and they are call ed the base
vectors or basis of the vector space V. For example, the three unit vectors
e
1
1; 0; 0; e
2
0; 1; 0 , and e
3
0; 0; 1 span E
3
because every vector in E
3
is expressible as a linear combination of e
1
, e
2
, and e
3
. But the following three
vectors in E
3
do not span E
3
: 1
ji
1; 1; 2 ; 2
ji
1; 0; 1, and 3
ji
2; 1; 3.
Base vectors are very useful in a variety of problems since it is often possible to
study a vector space by ®rst studying the vectors in a base set, then extending the
results to the rest of the vector space. Therefore it is desirable to keep the spanning
set as small as possible. Finding the spanning sets for a vector space depends upon
the notion of linear independence.
We say that a ®nite set of n vectors 1
ji
; 2
ji
; ...; r
ji
; ...; n
ji
, none of which is a
null vector, is linearly independent if no set of non-zero numbers a
k
exists such
that
X
n
k1
a
k
k
ij
j0i: 5:8
In other words, the set of vectors is linearly independent if it is impossible to
construct the null vector from a linear combination of the vectors except when all
204
LINEAR VECTOR SPACES

the coecients vanish. For example, non-zero vectors 1jiand 2jiof E
2
that lie
along the same coordinate axis, say x
1
, are not linearly independent, since we can
write one as a mult iple of the other: 1
ji
a 2
ji
, where a is a scalar which may be
positive or negative. That is, 1
ji
and 2
ji
depend on each other and so they are not
linearly independent. Now let us move the term a 2
ji
to the left hand side and the
result is the null vector: 1
ji
ÿ a 2
ji
0
ji
. Thus, for these two vectors 1
ji
and 2
ji
in
E
2
, we can ®nd two non-zero numbers (1, ÿa such that Eq. (5.8) is satis®ed, and
so they are not linearly independent.
On the other hand, the n vectors 1
ji
; 2
ji
; ...; r
ji
; ...; n
ji
are linearly dependent if
it is possible to ®nd scalars a
1
; a
2
; ...; a
n
, at least two of which are non-zero, such
that Eq. (5.8) is satis®ed. Let us say a
9
6 0. Then we could express 9
ji
in terms of
the other vectors
9
ji
X
n
i1;69
ÿa
i
a
9
i
ji
:
That is, the n vectors in the set are linearly dependent if any one of them can be
expressed as a linea r combination of the remaining n ÿ 1 vectors.
Example 5.4
The set of three vectors 1
ji
2; ÿ1; 0; 3,2
ji
1; 2; 5; ÿ1; 3
ji
7; ÿ1; 5; 8 is
linearly dependent, since 3 1ji2jiÿ3ji0ji.
Example 5.5
The set of three unit vectors e
1
ji
1; 0; 0 ; e
2
ji
0; 1; 0, and e
3
ji
0; 0; 1 in
E
3
is linearly independent. To see this, let us star t with Eq. (5.8) which now takes
the form
a
1
e
1
ji
a
2
e
2
ji
a
3
e
3
ji
0
ji
or
a
1
1; 0; 0a
2
0; 1; 0a
3
0; 0; 10; 0; 0
from which we obtain
a
1
; a
2
; a
3
0; 0; 0 ;
the set of three unit vectors e
1
ji
; e
2
ji
, and e
3
ji
is therefore linearly independent.
Example 5.6
The set S of the following four matrices
1
ji
10
00
; 2
ji
01
00
; j3
i
00
10
; 4
ji
00
01
;
205
LINEAR INDEPENDENCE, BASES, AND DIMENSIONALITY
