Chow T.L. Mathematical Methods for Physicists: A Concise Introduction

Подождите немного. Документ загружается.

Multiplying Eq. (5.33) from the left by

, we obtain



jvi  

jvi;

which using the fact



, can be rewritten as



jvi  

jvi:

Thus,

jvi is an eigenvector of

belonging to eigenvalue  .If is non-degen-

erate, then

jvi should be linearly dependent on jvi, so that

a

jvi  bjvi0; with a 6 0 and b 6 0:

It follows that

jviÿb=ajviÿjvi:

If A is degenerate, then the matter becomes a little complicated. We now state

the results without proof. There are three possibilities:

(1) The degenerate eigenvectors (that is, the linearly independent eigenvectors

belonging to a degenerate eigenvalue) of

are degenerate eigenvectors of

also.

(2) The degenerate eigenvectors of

belong to diÿerent eigenva lues of

. In this

case, we say that the degeneracy is removed by the Hermitian operator

(3) Every degenerate eigenvector of

is not an eigenvector of

. But there are

linear combinations of the degenerate eigenvectors, as many in number as

the degrees of degeneracy, which are degenerate eigenvectors of

but

are non-degenerate eigenvectors of

. Of course, the degeneracy is removed

Function spaces

We have seen that functions can be elements of a vector space. We now return to

this theme for a more detailed analysis. Consider the set of all functions that are

continuous on some interval. Two such functions can be added together to con-

struct a third function hx:

hxf xgx; a  x  b;

where the plus symbol has the usual operational meaning of `add the value of f at

the point x to the value of g at the same point.'

A function f x can also be multiplied by a number k to give the function px:

pxk  f x; a  x  b :

226

LINEAR VECTOR SPACES

The centred dot, the multiplication symbol, is again understood in the conven-

tional meani ng of `multiply by k the value of f x at the point x.'

It is evident that the following conditions are satis®ed:

(a) By adding two continuous functions, we obtain a continuous function.

(b) The multiplication by a scalar of a continuous function yiel ds again a con-

tinuous function.

addition to any other function does not alter this function.

(d) For any function f x there exists a function ÿ1f x, which satis®es

f x  ÿ1f x  0:

Comparing these statements with the axioms for linear vector spaces (Axioms

A.1±A.8), we see clearly that the set of all continuous functions de®ned on some

interval forms a linear vector space; this is called a function space. We shall

consider the entire set of values of a function f x as representing a vector jf i

of this abstract vector space F (F stands for function space). In other words, we

shall treat the number f x at the point x as the component with `index x'ofan

abstract vector jf i. This is quite similar to what we did in the case of ®nite-

dimensional spaces when we associated a component a

of a vector with each

value of the index i. The only diÿerence is that this index assumed a discrete set

of values 1, 2, etc., up to N (for N-dimensional space), whereas the argument x of

a function f x is a continuous variable. In other words, the function f x has an

in®nite number of components, namely the values it takes in the continuum of

points labeled by the real variable x. However, two questions may be raised.

The ®rst question concerns the orthonormal basis. The components of a vector

are de®ned with respect to some basis and we do not know which basis has been

(or could be) chosen in the function space. Unfortunately, we have to postpone

the answer to this question. Let us merely note that, once a basis has been chosen,

we work only with the components of a vector. Therefore, provided we do not

change to other basis vectors, we need not be concerned about the particular basis

that has been chosen.

The second question is how to de®ne an inner product in an in®nite-dimen-

sional vector space. Suppose the function f  x describes the displacement of a

string clamped at x  0 and x  L. We divide the interval of length L into N equal

parts and measure the displacements f x

f

at N point x

; i  1; 2; ...; N.At

®xed N, the functions are elements of a ®nite N-dimensional vector space. An

inner product is de®ned by the expression

fhjgi

i1

227

FUNCTION SPACES

For a vibrating string, the space is real and there is no need to conjugate anything.

To improve the description, we can increase the number N. However, as

N !1 by increasing the number of points without limit, the inner product

diverges as we subdivide further and further. The way out of this is to modify

the de®nition by a positive prefactor   L=N which does not violate any of the

axioms for the inner product. But now

 lim

!0

i1

 !

f xgxdx;

by the usual de®nition of an integral. Thus the inner product of two functions is

the integral of their product. Two functions are orthogonal if this inner product

vanishes, and a function is normalized if the integral of its square equals unity.

Thus we can speak of an orthonormal set of functions in a function space just as

in ®nite dimensions. The following is an example of such a set of functions de®ned

in the interval 0  x  L and vanishing at the end points:

! mx



sin

mx

; m  1; 2; ...; 1;



sin

mx

sin

nx

dx  

For the details, see `Vibrating strings' of Chapter 4.

In quantum mechanics we often deal with complex functions and our de®nition

of the inner prod uct must then modi®ed. We de®ne the inner product of f x and

gx as



f *xgxdx;

where f * is the complex conjugate of f. An orthonormal set for this case is

mx



2

imx

; m  0;  1;  2; ...;

which spans the space of all functions of period 2 with ®nite norm. A linear

vector spac e with a complex-type inner product is called a Hilb ert space.

Where and how did we get the orthonormal functions? In general, by solving

the eigenvalue equation of some Hermitian operator. We give a simple example

here. Consi der the derivative operator D  d=dx:

Df xdf x=dx; Djf idjf i=dx:

However, D is not Hermitian, because it does not meet the condition:

f *x

dgx

dx 

g*x

df x



228

LINEAR VECTOR SPACES

Here is why:

g*x

df x





gx

df *x

 gf*

f *x

dgx

dx:

It is easy to see that hermiticity of D is lost on two counts. First we have the term

coming from the en d points. Second the integral has the wrong sign. We can ®x

both of these by doing the following:

(a) Use operator ÿiD. The extra i will change sign under conjugation and kill

the minus sign in front of the integral.

(b) Restrict the functions to those that are periodic: f 0f L.

Thus, ÿiD is a Hermitian operator on period functions. Now we have

ÿi

df x

 f x;

where  is the eigenvalue. Simple integration gives

f xAe

ix

Now the periodicity requirement gives

iL

 e

i0

 1

from which it follows that

  2m=L; m  0; 1; 2;

and the normalization condition gives

A 



Hence the set of orthonormal eigenvectors is given by

x



2imx=L

In quantum mechanics the eigenvalue equation is the Schro

dinger equation and

the Hermitian operator is the Hamiltonian operator. Quantum mechanically, a

system with n degrees of freedom which is classically speci®ed by n generalized

coordinates q

; ...; q

; q

is speci®ed at a ®xed instant of time by a wave function

ýq

; q

; ...; q

 whose norm is unity, that is,



ýq

; q

; ...; q



; dq

; ...; dq

 1;

229

FUNCTION SPACES

the integration being over the accessible values of the coordinates q

; q

; ...; q

The set of all such wave functions with unit norm spans a Hilbert space H. Every

possible state of the system is represented by a function in this Hilbert space, and

conversely, every vector in this Hilbert space represents a possible state of the

system. In additio n to depending on the coordinates q

; q

; ...; q

, the wave func-

tion depends also on the time t, but the dependence on the qs and on t are

essentially diÿerent. The Hilbert space H is formed with respect to the spatial

coordinates q

; q

; ...; q

only, for exampl e, the inner product is formed with

respect to the qs only, and one wave function ýq

; q

; ...; q

) states its complete

spatial dependence. On the other hand the states of the system at diÿerent instants

of time t

; t

; ... are given by the diÿerent wave functions

q

; q

; ...; q

;ý

q

; q

; ...; q

... of the Hilbert space.

Problems

5.1 Prove the three main properties of the dot product given by Eq. (5.7).

5.2 Show that the points on a line V passing through the origin in E

form a

linear vector space under the addition and scalar multiplication operations

for vectors in E

Hint: The points of V satisfy parametric equations of the form

 at; x

 bt; x

 ct; ÿ1< t < 1:

5.3 Do all Hermitian 2  2 matrices form a vector space under addition? Is there

any requirement on the scalars that multiply them?

5.4 Let V be the set of all points (x

; x

)inE

that lie in the ®rst quadrant; that

is, such that x

 0 and x

 0. Show that the set V fails to be a vector space

under the operations of addition and scalar multiplication.

Hint: Consider u=(1, 1) which lies in V. Now form the scalar multiplication

ÿ1u ÿ1; ÿ1 ; where is this point located?

5.5 Show that the set W of all 2  2 matrices having zeros on the principal

diagonal is a subspace of the vector space M

of all 2  2 matrices.

5.6 Show that j W i4; ÿ1; 8 is not a linear combination of jUi1; 2; ÿ1

and jVi6; 4; 2.

5.7 Show that the following three vectors in E

cannot serve as base vectors of E

1; 1; 2; 2

1; 0; 1 ; and 3

2; 1; 3:

5.8 Determine which of the following lie in the space spanned by jf icos

and jgisin

x:(a) cos 2 x; b3  x

; c1; dsin x.

5.9 Determine whether the three vectors

1; ÿ2; 3 ; 2

5; 6; ÿ1; 3

3; 2; 1 

are linearly dependent or independent.

230

LINEAR VECTOR SPACES

5.10 Given the following three vectors from the vector space of real 2  2

matrices:





; 2





; 3



ÿ2 ÿ1

0 ÿ2



;

determine whether they are linearly dependent or independent.

5.11 If S  1

; 2

; ...; n

jifg

is a basis for a vector space V, show that every set

with more than n vectors is linearly dependent.

5.12 Show that any two bases for a ®nite-dimensional vector space have the same

number of vectors.

5.13 Consider the vector space E

with the Euclidean inner product. Apply the

Gram±Schmidt process to transform the basis

j1i1; 1; 1; j2i0; 1; 1; j3i0; 0; 1

into an orthonormal basis.

5.14 Consider the two linearly independent vectors of Example 5.10:

jUi3 ÿ 4ij1i5 ÿ 6ij2i;

jWi1 ÿ i j1i2 ÿ 3ij2i;

where j1i and j2i are an orthonormal basis. Apply the Gram±Schmidt pro-

cess to transform the two vectors into an orthonormal basis.

5.15 Show that the eigenvalue of the square of an operator is the square of the

eigenvalue of the operator.

5.16 Show that if, for a given

, both operators

ÿ1

and

ÿ1

exist, then

ÿ1



ÿ1



ÿ1

5.17 Show that if a unitary operator

can be written in the form

 1  ie

where e is a real in®nitesimally small number, then the operator

Hermitian.

5.18 Show that the diÿerential ope rator



is linear and Hermitian in the space of all diÿerentiable wave functions x

that, say, vanish at both ends of an interval (a, b).

5.19 The translation operator Ta is de®ned to be such that Tax

x  a. Show that:

(a) Ta may be expressed in terms of the operator



;

231

PROBLEMS

(b) Ta is unitary.

5.21 Verify that:

a

sin

mx

sin

nx

dx  

b



2

imÿn

dx  

232

LINEAR VECTOR SPACES

Functions of a complex variable

The theory of functions of a complex variable is a basic part of mathematical

analysis. It provides some of the very useful mathematical tools for physicists and

engineers. In this chapter a brief introduction to complex variables is presented

which is intended to acquaint the reader with at least the rudiments of this

important subject.

Complex numbers

The number system as we know it today is a result of gradual development. The

natural numbers (positive integers 1, 2, ...) were ®rst used in counting. Negative

integers and zero (that is, 0, ÿ1; ÿ2; ...) then arose to permit solutions of equa-

tions such as x  3  2. In order to solve equations such as bx  a for all integers

a and b where b 6 0, rational numbers (or fractions) were introduced. Irrational

numbers are numbers which cannot be expressed as a/b,witha and b integers and

b 6 0, such as



 1:41423; 3:14159

Rational and irrational numbers are all real numbers. However, the real num-

ber system is still incomplete. For example, there is no real number x which

satis®es the algebraic equation x

 1  0: x 



ÿ1

. The problem is that we

do not know what to make of



ÿ1

because there is no real number whose sq uare

is ÿ1. Euler introduced the symbol i 



ÿ1

in 1777 years later Gauss used the

notation a  ib to denote a complex number, where a and b are real numbers.

Today, i 



ÿ1

is called the unit imaginary number.

In terms of i, the answer to equation x

 1  0isx  i. It is postulated that i

will behave like a real number in all manipulations involving addition and multi-

plication.

We now introduce a general complex number, in Cartesian form

z  x  iy 6:1

233

and refer to x and y as its real and imaginary parts and denote them by the

symbols Re z and Im z, respectively. Thus if z ÿ3  2i, then Re z ÿ3 and

Im z 2.

A number with just y 6 0 is called a pure imaginary number.

The complex conjugate, or brie¯y conjugate, of the complex number z  x  iy

z*  x ÿ iy 6:2

and is called `z-star'. Sometimes we write it



z and call it `z-bar'. Complex con-

jugation can be viewed as the process of replacing i by ÿi within the complex

number.

Basic operations with complex numbers

Two complex numbers z

 x

 iy

and z

 x

 iy

are equal if and only if

 x

and y

 y

In performing operations with complex numbers we can proceed as in the

algebra of real numbers, replacing i

by ÿ1 when it occurs. Given two complex

numbers z

and z

where z

 a  ib ; z

 c  id, the basic rules obeyed by com-

plex numbers are the following:

(1) Addition:

 z

a  ibc  ida  cib  d:

(2) Subtraction:

ÿ z

a  ibÿc  ida ÿ cib ÿ d:

(3) Multiplication:

a  ibc  idac ÿ bdiad ÿ bc:

(4) Division:



a  ib

c  id



a  ibc ÿ id

c  idc ÿ id



ac  bd

 d

 i

bc ÿ ad

 d

Polar form of complex numbers

All real numbers can be visualized as points on a straight line (the x-axis). A

complex number, containing two real numbers, can be represented by a point in a

two-dimensional xy plane, known as the z plane or the complex plane (also

known as the Gauss plane or Argand diagram). The complex variable

z  x  iy and its complex conjugation z* are labeled in Fig. 6.1.

234

FUNCTIONS OF A COMPLEX VARIABLE

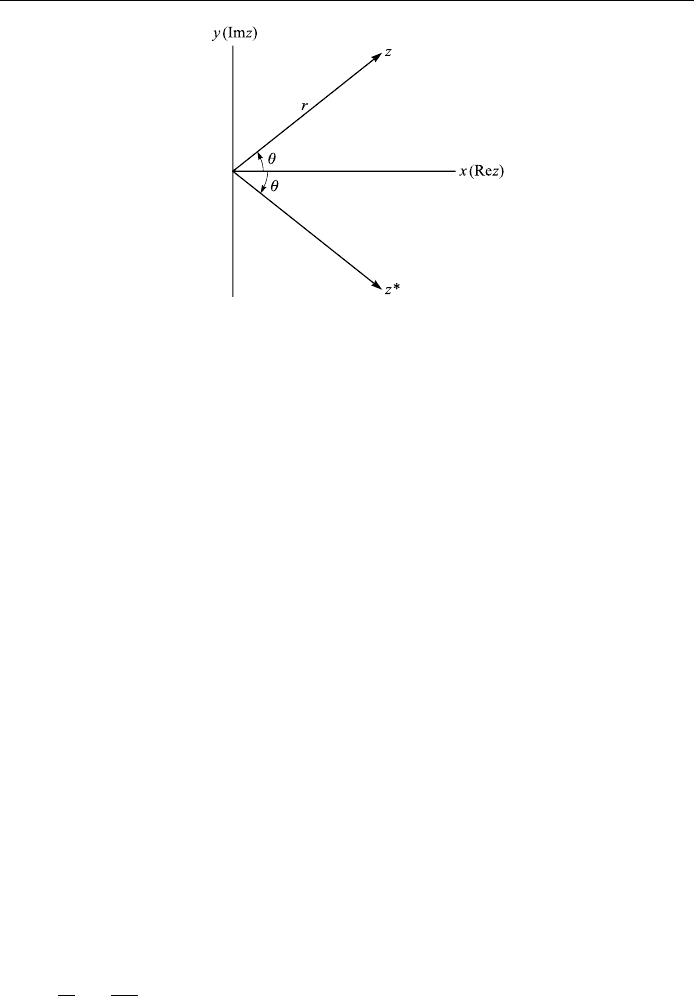
The complex variable can also be represented by the plane polar coordinat es

(r;):

z  rcos   i sin :

With the help of Euler's formula

i

 cos   i sin ;

we can rewrite the last equation in polar form:

z  rcos   i sin re

i

; r 



 y





zz*

: 6:3

r is called the modulus or absolute value of z, denoted by jzj or mod z; and  is

called the phase or argument of z and it is denoted by arg z. For any complex

number z 6 0 there corresponds only one value of  in 0    2. The absolute

value of z has the following properties. If z

; z

; ...; z

are complex numbers, then

we have:

(1) jz

z

jjz

jjz

jjz

(2)



; z

6 0.

(3) jz

 z

z

jjz

jjz

jjz

(4) jz

 z

jjz

jÿjz

Complex numbers z  re

i

with r  1 have jzj1 and are called unimodul ar.

235

COMPLEX NUMBERS

Figure 6.1. The complex plane.