Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


We may imagine them as lying on a circle of unit radius in the complex plane.
Special poi nts on this circle are
0 1
=2 i
ÿ1
ÿ=2 ÿi:
The reader should know these points at all times.
Sometimes it is easier to use the polar form in manipulations. For example, to
multiply two complex numbers, we multiply their moduli and add their phases; to
divide, we divide by the modulus and subtract the phase of the denominato r:
zz
1
re
i
r
1
e
i
1
rr
1
e
i
1
;
z
z
1
re
i
r
1
e
i
1
r
r
1
e
iÿ
1
:
On the other hand to add two complex numbers we have to go back to the
Cartesian forms, add the components and revert to the polar form.
If we view a complex number z as a vector, then the multiplicati on of z by e
i
(where is real) can be interpreted as a rotation of z counterclockwise through
angle ; and we can consider e
i
as an operator which acts on z to produce this
rotation. Simi larly, the multiplication of two complex numbers represents a rota-
tion and a change of length : z
1
r
1
e
i
1
; z
2
r
2
e
i
2
, z
1
z
2
r
1
r
2
e
i
1
2
; the new
complex number has length r
1
r
2
and phase
1
2
.
Example 6.1
Find 1 i
8
.
Solution: We ®rst write z in polar form: z 1 i rcos i sin , from which
we ®nd r
2
p
; =4. Then
z
2
p
cos =4 i sin =4
2
p
e
i=4
:
Thus
1 i
8
2
p
e
i=4
8
16e
2i
16:
Example 6.2
Show that
1
3
p
i
1 ÿ
3
p
i
þ!
10
ÿ
1
2
i
3
p
2
:
236
FUNCTIONS OF A COMPLEX VARIABLE

1 i
3
p
1 ÿ i
3
p
þ!
10
2e
i=3
2e
ÿi=3
þ!
10
e
2i=3
10
e
20i=3
e
6i
e
2i=3
1cos2=3i sin2=3ÿ
1
2
i
3
p
2
:
De Moivre's theorem and roots of complex numbers
If z
1
r
1
e
i
1
and z
2
r
2
e
i
2
, then
z
1
z
2
r
1
r
2
e
i
1
2
r
1
r
2
cos
1
2
i sin
1
2
:
A generalization of this leads to
z
1
z
2
z
n
r
1
r
2
r
n
e
i
1
2
n
r
1
r
2
r
n
cos
1
2
n
i sin
1
2
n
;
if z
1
z
2
z
n
z this becomes
z
n
re
i
n
r
n
cosni sinn;
from which it follows that
cos i sin
n
cosni sinn; 6:4
a result known as De Moivre's theorem. Thus we now have a general rule for
calculating the nth power of a complex number z. We ®rst write z in polar form
z rcos i sin , then
z
n
r
n
cos i sin
n
r
n
cos n i sin n: 6:5
The general rule for calculating the nth root of a complex number can now be
derived without diculty. A number w is called an nth root of a complex number
z if w
n
z, and we write w z
1=n
.Ifz rcos i sin , then the complex num-
ber
w
0
r
n
p
cos
n
i sin
n
is de®nitely the nth root of z because w
n
0
z. But the numbers
w
k
r
n
p
cos
2 k
n
i sin
2k
n
; k 1; 2; ...; n ÿ 1;
are also nth roots of z because w
n
k
z. Thus the general rule for calculating the nth
root of a complex number is
w
r
n
p
cos
2 k
n
i sin
2 k
n
; k 0; 1; 2; ...; n ÿ 1: 6:6
237
COMPLEX NUMBERS
It is customary to call the number corresponding to k 0 (that is, w
0
) the princi -
pal root of z.
The nth roots of a complex number z are always located at the vertices of a
regular polygon of n sides inscribed in a circle of radius
r
n
p
about the origin.
Example 6.3
Find the cube roots of 8.
Solution: In this case z 8 i0 rcos i sin ; r 2 and the principal argu-
ment 0. Formula (6.6) then yields
8
3
p
2 cos
2k
3
i sin
2k
3
; k 0; 1; 2:
These roots are plotted in Fig. 6.2:
2 k 0; 08;
ÿ1 i
3
p
k 1; 1208;
ÿ1 ÿ i
3
p
k 2; 2408:
Functions of a complex variable
Complex numbers z x iy become variables if x or y (or both) vary. Then
functions of a complex variable may be formed. If to each value which a complex
variable z can assume there corresponds one or more values of a complex variable
w, we say that w is a function of z and write w f z or w gz, etc. The
variable z is sometimes called an independent variable, and then w is a depende nt
238
FUNCTIONS OF A COMPLEX VARIABLE
Figure 6.2. The cube roots of 8.
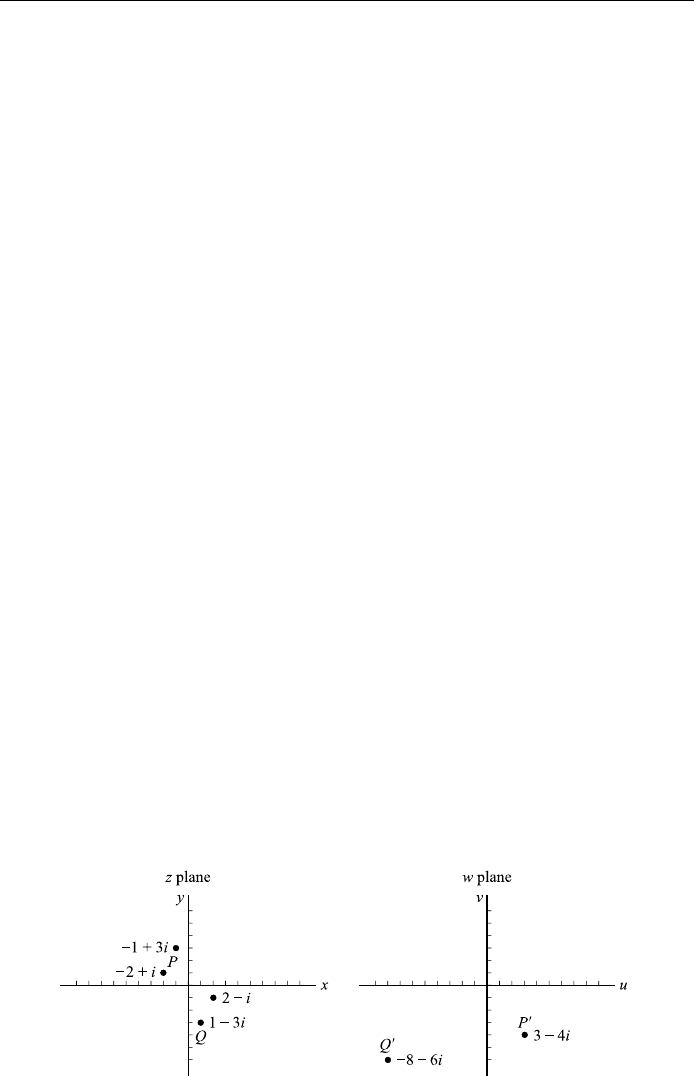
variable. If only one value of w corresponds to each value of z, we say that w is a
single-valued function of z or that f z is single-valued; and if more than one value
of w corresponds to each value of z, w is then a multiple-valued function of z. For
example, w z
2
is a singl e-valued function of z, but w
z
p
is a doubl e-valued
function of z. In this chapter, whenever we speak of a function we shall mean a
single-valued function, unless otherwise stated.
Mapping
Note that w is also a complex variable and so can be written in the form
w u iv f x iy; 6:7
where u and v are real. By equating real and imaginary parts this is seen to be
equivalent to
u u x; y; v vx; y: 6:8
If w f z is a single-valued function of z, then to each point of the complex z
plane, there corresponds a point in the complex w plane. If f z is multiple-valued,
a point in the z plane is mapped in general into more than one point. The
following two examples show the idea of mapping clearly.
Example 6.4
Map w z
2
r
2
e
2i
:
Solution: This is single-valued function. The mapping is unique, but not
one-to-one. It is a two-to-one mapping, since z and ÿz give the same square.
For example as shown in Fig. 6.3, z ÿ2 i and z 2 ÿ i are mapped to the
same point w 3 ÿ 4i;andz 1 ÿ 3i and ÿ1 3i are mapped into the same
point w ÿ8 ÿ 6i.
The line joining the points Pÿ2; 1 and Q1; ÿ3 in the z-plane is mapped by
w z
2
into a curve joining the image points P
0
3; ÿ4 and Q
0
ÿ8; ÿ6. It is not
239
MAPPING
Figure 6.3. The mapping function w z
2
.
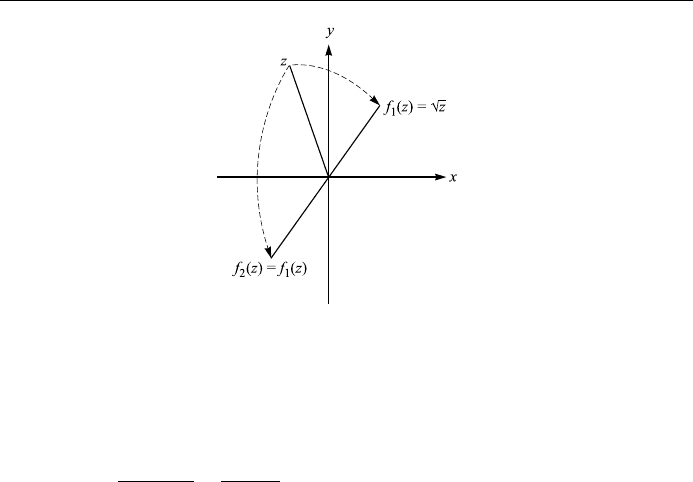
very dicult to determine the equation of this curve. We ®rst need the equation of
the line joining P and Q in the z plane. The parametric equations of the line
joining P and Q are given by
x ÿÿ2
1 ÿÿ2
y ÿ 1
ÿ3 ÿ 1
t or x 3t ÿ 2 ; y 1 ÿ 4t:
The equation of the line PQ is then given by z 3t ÿ 2 i1 ÿ 4t. The curve in
the w plane into which the line PQ is mapped has the equation
w z
2
3t ÿ 2 i1 ÿ 4t
2
3 ÿ 4t ÿ 7t
2
iÿ4 22t ÿ 24t
2
;
from which we obtain
u 3 ÿ 4t ÿ 7t
2
; v ÿ4 22t ÿ 24t
2
:
By assigning various values to the parameter t, this curve may be graphed.
Sometimes it is convenient to superimpose the z and w plan es. Then the images
of various points are located on the same plane and the function w f z may be
said to transform the complex plane to itself (or a part of itself).
Example 6.5
Map w f z
z
p
; z re
i
:
Solution: There are two square roots: f
1
re
i
r
p
e
i=2
; f
2
ÿf
1
r
p
e
i2=2
.
The function is double-valued, and the mapping is one-to-two. This is shown in
Fig. 6.4, where for simplicity we have used the same complex plane for both z and
w f z.
Branch lines and Riemann surfaces
We now take a close look at the function w
z
p
of Example 6.5. Suppose we allow z
to make a complete counterclockwise motion around the origin starting from point
240
FUNCTIONS OF A COMPLEX VARIABLE
Figure 6.4. The mapping function w
z
p
:
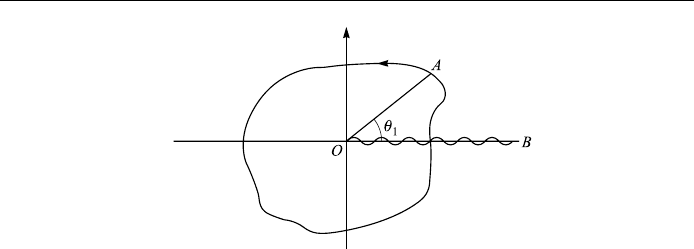
A, as shown in Fig. 6.5. At A,
1
and w
r
p
e
i=2
. After a complete circuit back
to A;
1
2 and w
r
p
e
i2=2
ÿ
r
p
e
i=2
. However, by making a second
complete circuit back to A,
1
4, and so w
r
p
e
i4=2
r
p
e
i=2
; that is,
we obtain the same value of w with which we started.
We can describe the above by stating that if 0 <2 we are on one branch of
the multiple-valued function
z
p
, while if 2 <4 we are on the other branch
of the function. It is clear that each branch of the function is single-valued . In
order to keep the function single-valued, we set up an arti®cial barrier such as OB
(the wavy line) which we agree not to cross. This arti®cial barrier is called a
branch line or branch cut, point O is called a branch point. Any other line
from O can be used for a branch line.
Riemann (George Friedrich Bernhard Riemann, 1826±1866) suggest ed another
way to achieve the purpose of the branch line described above. Imagine the z plane
consists of two sheets superimposed on each other. We now cut the two sheets along
OB and join the lower edge of the bottom sheet to the upper edge of the top sheet.
Then on starting in the bottom sheet and making one complete circuit about O we
arrive in the top sheet. We must now imagine the other cut edges to be joined
together (independent of the ®rst join and actually disregarding its existence) so
that by continuing the circuit we go from the top sheet back to the bottom sheet.
The collection of two sheets is called a Riemann surface corresponding to the
function
z
p
. Each sheet corresponds to a branch of the functi on and on each
sheet the function is singled-valued. The concept of Riemann surfaces has the
advantage that the various values of multiple-valued functions are obtained in a
continuous fashion.
The diÿerential calculus of functions of a complex variable
Limits and continuity
The de®nitions of limits and continuity for functions of a complex variable are
similar to those for a real variable. We say that f z has limit w
0
as z approaches
241
Figure 6.5. Branch cut for the function w
z
p
.
DIFFERENTIAL CALCULUS

z
0
, which is written as
lim
z!z
0
f zw
0
; 6:9
if
(a) f z is de®ned and single-valued in a neighborhood of z z
0
, with the
possible exception of the point z
0
itself; and
(b) given any positive number " (however small), there exists a positive number
such that f zÿw
0
jj
<"whenever 0 < z ÿ z
0
jj
<.
The limit must be independent of the manner in which z approaches z
0
.
Example 6.6
(a)Iff zz
2
, prove that lim
z!z
0
; f zz
2
0
(b) Find lim
z!z
0
f z if
f z
z
2
z 6 z
0
0 z z
0
:
(
Solution: (a) We must show that given any ">0 we can ®nd (depending in
general on ") such that jz
2
ÿ z
2
0
j <"whenever 0 < jz ÿ z
0
j <.
Now if 1, then 0 < jz ÿ z
0
j <implies that
z ÿ z
0
jj
z z
0
jj
<z z
0
jj
z ÿ z
0
2z
0
jj
;
z
2
ÿ z
2
0
ÿ
ÿ
ÿ
ÿ
< z ÿ z
0
jj
2 z
0
jj
< 1 2 z
0
jj
:
Taking as 1 or "=1 2jz
0
j, whichever is smaller, we then have jz
2
ÿ z
2
0
j <"
whenever 0 < jz ÿ z
0
j <, and the required result is proved.
(b) There is no diÿerence between this problem and that in part (a), since in
both cases we exclude z z
0
from consideration. Hence lim
z!z
0
f zz
2
0
. Note
that the limit of f z as z ! z
0
has nothing to do with the value of f z at z
0
.
A function f z is said to be continuous at z
0
if, given any ">0, there exists a
>0 such that f zÿf z
0
jj
<" whenever 0 < z ÿ z
0
jj
<. This implies three
conditions that must be met in order that f z be continuous at z z
0
:
(1) lim
z!z
0
f zw
0
must exist;
(2) f z
0
must exist, that is, f z is de®ned at z
0
;
(3) w
0
f z
0
.
For example, complex polynomials,
0
1
z
1
2
z
2
n
z
n
(where
i
may be
complex), are continuous everywhere. Quotients of polynomials are continuous
whenever the denominator does not vanish. The following example provides
further illustration.
242
FUNCTIONS OF A COMPLEX VARIABLE

A function f z is said to be continuous in a region R of the z plane if it is
continuous at all points of R.
Points in the z plane where f z fails to be continuous are called discontinuities
of f z, and f z is said to be discontinuous at these points. If lim
z!z
0
f z exists
but is not equal to f z
0
, we call the point z
0
a removable discontinuity, since by
rede®ning f z
0
to be the same as lim
z!z
0
f z the function becomes continuous.
To exami ne the continuity of f z at z 1, we let z 1=w and examine the
continuity of f 1=w at w 0.
Derivatives and analytic functions
Given a continuous, single-valued function of a complex variable f z in some
region R of the z plane, the derivative f
0
z df=dz at some ®xed point z
0
in R is
de®ned as
f
0
z
0
lim
z!0
f z
0
zÿf z
0
z
; 6:10
provided the limit exists independently of the manner in which z ! 0. Here
z z ÿ z
0
,andz is any point of some neighborhood of z
0
.Iff
0
z exists at z
0
and every point z in some neighborhood of z
0
, then f z is said to be analytic at z
0
.
And f z is analytic in a region R of the complex z plane if it is analytic at every
point in R.
In order to be analytic, f z must be single-valued and continuous. It is
straightforward to see this. In view of Eq. (6.10), whenever f
0
z
0
exists, then
lim
z!0
f z
0
zÿf z
0
lim
z!0
f z
0
zÿf z
0
z
lim
z!0
z 0
that is,
lim
z!0
f zf z
0
:
Thus f is necessarily continuous at any point z
0
where its derivative exists. But the
converse is not necessarily true, as the following example shows.
Example 6.7
The functi on f zz* is continuous at z
0
, but dz*=dz does not exist anywhere. By
de®nition,
dz*
dz
lim
z!0
z z* ÿ z*
z
lim
x;y!0
x iy x iy* ÿx iy*
x iy
lim
x;y!0
x ÿ iyx ÿ i y ÿx ÿ iy
x iy
lim
x;y!0
x ÿ iy
x iy
:
243
DIFFERENTIAL CALCULUS

If y 0, the required limit is lim
x!0
x=x 1. On the other hand, if
x 0, the required limit is ÿ1. Then since the limit depend s on the manner
in which z ! 0, the derivative does not exist and so f zz * is non-analytic
everywhere.
Example 6.8
Given f z2z
2
ÿ 1, ®nd f
0
z at z
0
1 ÿ i.
Solution:
f
0
z
0
f
0
1 ÿ i lim
z!1ÿi
2z
2
ÿ 1ÿ21 ÿ i
2
ÿ 1
z ÿ1 ÿ i
lim
z!1ÿi
2z ÿ1 ÿ iz 1 ÿ i
z ÿ1 ÿ i
lim
z!1ÿi
2z 1 ÿ i 41 ÿ i:
The rules for diÿerentiating sums, products, and quotients are, in general, the
same for complex functions as for real-valued functions. That is, if f
0
z
0
and
g
0
z
0
exist, then:
(1) f g
0
z
0
f
0
z
0
g
0
z
0
;
(2) fg
0
z
0
f
0
z
0
gz
0
f z
0
g
0
z
0
;
(3)
f
g
0
z
0
gz
0
f
0
z
0
ÿf z
0
g
0
z
0
gz
0
2
; if g
0
z
0
60:
The Cauchy±Riemann conditions
We call f z analytic at z
0
,iff
0
z exists for all z in some neighborhood of z
0
;
and f z is analytic in a region R if it is analytic at every point of R. Cauchy and
Riemann provided us with a simple but extremely important test for the analyti-
city of f z. To deduce the Cauchy±Riemann conditions for the analyticity of
f z, let us return to Eq. (6.10):
f
0
z
0
lim
z!0
f z
0
zÿf z
0
z
:
If we write f zux; yivx; y, this becomes
f
0
z lim
x;y!0
ux x; y yÿux; yisame for v
x iy
:
There are of course an in®nite number of ways to approach a point z on a two-
dimensional surface. Let us consider two possible approaches ± along x and along
244
FUNCTIONS OF A COMPLEX VARIABLE

y. Suppose we ®rst take the x route, so y is ®xed as we change x, that is, y 0
and x ! 0, and we have
f
0
z lim
x!0
ux x; yÿux; y
x
i
vx x; yÿvx; y
x
@u
@x
i
@v
@x
:
We next take the y route, and we have
f
0
z lim
y!0
ux; y yÿux; y
i y
i
vx; y yÿvx; y
iy
ÿi
@u
@y
@v
@y
:
Now f z cannot possibly be analytic unless the two derivatives are identical.
Thus a necessary condition for f z to be analytic is
@u
@x
i
@v
@x
ÿi
@u
@y
@v
@y
;
from which we obtain
@u
@x
@v
@y
and
@u
@y
ÿ
@v
@x
: 6:11
These are the Cauchy±Riemann conditions, named after the French mathemati-
cian A. L. Cauchy (1789±1857) who discovered them, and the German mathema-
tician Riemann who made them fundamental in his development of the theory of
analytic functions. Thus if the function f zux; yivx; y is analytic in a
region R, then ux; y and vx; y satisfy the Cauchy±Riemann conditions at all
points of R.
Example 6.9
If f zz
2
x
2
ÿ y
2
2ixy, then f
0
z exists for all z: f
0
z2z,and
@u
@x
2x
@v
@y
; and
@u
@y
ÿ2y ÿ
@v
@x
:
Thus, the Cauchy±Riemann equations (6.11) hold in this example at all points z.
We can also ®nd examples in which ux; y and vx; y satisfy the Cauchy±
Riemann conditions (6.11) at z z
0
, but f
0
z
0
doesn't exist. One such example
is the following:
f zux; yiv x; y
z
5
=jzj
4
if z 6 0
0ifz 0
(
:
The reader can show that ux; y and vx; y satisfy the Cauchy±Riemann condi-
tions (6.11) at z 0, but that f
0
0 does not exist. Thus f z is not analytic at
z 0. The proof is straightforward, but very tedious.
245
DIFFERENTIAL CALCULUS
