Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.

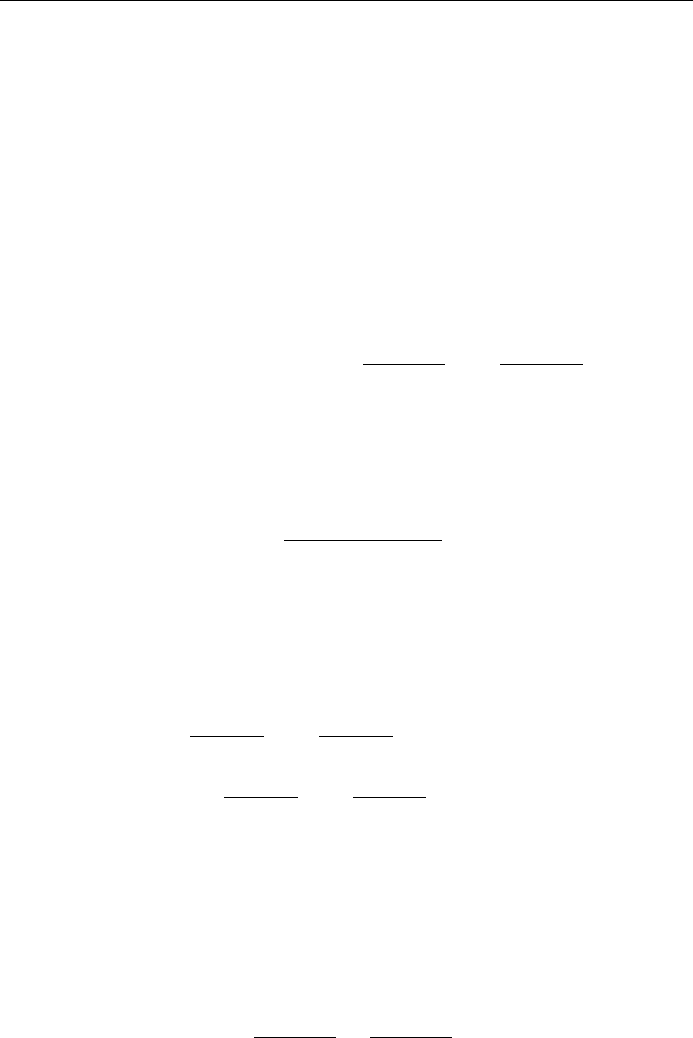
However, the Cauchy±Riemann conditions do imply analyticity provided an
additional hypothesis is added:
Given f zux; yivx; y,ifux; y and vx; y are contin-
uous with continuous ®rst partial derivatives and satisfy the
Cauchy±Riemann conditions (11) at all points in a region R,
then f z is analytic in R.
To prove this, we need the following result from the calculus of real-valued
functions of two variables: If hx; y;@h=@x, and @h=@y are continuous in some
region R about x
0
; y
0
, then there exists a function Hx; y such that
Hx; y!0asx; y!0; 0 and
hx
0
x; y
0
y ÿhx
0
; y
0
@hx
0
; y
0
@x
x
@hx
0
; y
0
@y
y
Hx; y
x
2
y
2
q
:
Let us return to
lim
z!0
f z
0
zÿf z
0
z
;
where z
0
is any point in region R and z x iy. Now we can write
f z
0
zÿf z
0
ux
0
x; y
0
yÿux
0
; y
0
i v x
0
x; y
0
yÿvx
0
; y
0
@ux
0
y
0
@x
x
@ux
0
y
0
@y
y Hx; y
x
2
y
2
q
i
@vx
0
y
0
@x
x
@vx
0
y
0
@y
y
Gx; y
x
2
y
2
q
;
where Hx; y!0 and Gx; y!0asx; y!0; 0.
Using the Cauchy±Riemann conditions and some algebraic manipulation we
obtain
f z
0
z ÿf z
0
@ux
0
; y
0
@x
i
@v x
0
; y
0
@x
x iy
Hx; yiGx; y
x
2
y
2
q
246
FUNCTIONS OF A COMPLEX VARIABLE

and
f z
0
zÿf z
0
z
@ux
0
; y
0
@x
i
@vx
0
; y
0
@x
Hx yiGx y
x
2
y
2
q
x iy
:
But
x
2
y
2
q
x iy
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
1:
Thus, as z ! 0, we have x; y!0; 0 and
lim
z!0
f z
0
zÿf z
0
z
@ux
0
; y
0
@x
i
@vx
0
; y
0
@x
;
which shows that the limit and so f
0
z
0
exist. Since f z is diÿerentiable at all
points in region R, f z is analytic at z
0
which is any point in R.
The Cauchy±Riemann equations turn out to be both necessary and sucient
conditions that f zux; yivx; y be analytic. Analytic functions are also
called regular or holomorphic functions. If f z is analytic everywhere in the ®nite
z complex plane, it is called an entire function. A function f z is said to be
singular at z z
0
, if it is not diÿerentiable there; the point z
0
is called a singular
point of f z.
Harmonic functions
If f zux; yivx; y is analyt ic in some region of the z plane, then at every
point of the region the Cauchy±Riemann conditions are satis®ed:
@u
@x
@v
@y
; and
@u
@y
ÿ
@v
@x
;
and therefore
@
2
u
@x
2
@
2
v
@x@y
; and
@
2
u
@y
2
ÿ
@
2
v
@y@x
;
provided these second derivatives exist. In fact, one can show that if f z is
analytic in some region R, all its derivatives exist and are continuous in R.
Equating the two cross terms, we obtain
@
2
u
@x
2
@
2
u
@y
2
0 6 :12a
throughout the region R.
247
DIFFERENTIAL CALCULUS

Similarly, by diÿerentiating the ®rst of the Cauch±Riemann equations with
respect to y, the second with respect to x, and subtracting we obtain
@
2
v
@x
2
@
2
v
@y
2
0: 6:12b
Eqs. (6.12a) and (6.12b) are Laplace's partial diÿeren tial equations in two inde-
pendent variables x and y. Any function that has continuous partial derivatives of
second order and that satis®es Laplace's equation is called a harmonic function.
We have shown that if f zux; yivx; y is analytic, then both u and v are
harmonic functions. They are called conjugate harmonic functions. This is a
diÿerent use of the word conjugate from that employed in determining z*.
Given one of two conjugate harmonic functions, the Cauchy±Riemann equa-
tions (6.11) can be used to ®nd the other.
Singular points
A point at which f z fails to be analytic is called a singular point or a singularity
of f z; the Cauchy±Riemann conditions break down at a singularit y. Various
types of singular points exist.
(1) Isolated singular points: The point z z
0
is called an isolated singular point
of f z if we can ®nd >0 such that the circle j z ÿ z
0
j encloses no
singular point other than z
0
. If no such can be found, we call z
0
a non-
isolated singularity.
(2) Poles: If we can ®nd a positive integer n such that
lim
z!z
0
z ÿ z
0
n
f zA 6 0, then z z
0
is called a pole of order n.If
n 1, z
0
is called a simple pole. As an example, f z1=z ÿ 2 has a
simple pole at z 2. But f z1=z ÿ 2
3
has a pole of order 3 a t z 2.
(3) Branch point: A functio n has a branch point at z
0
if, upon encircling z
0
and
returning to the starting point, the function does not return to the starting
value. Thus the function is multiple-valued. An example is f z
z
p
, which
has a branch point at z 0.
(4) Removable singularities: The singular point z
0
is called a removable singu-
larity of f z if lim
z!z
0
f z exists. For example, the singular point at z 0
of f zsinz=z is a removable singularity, since lim
z!0
sinz=z 1.
(5) Essential singularities: A function has an essential singularity at a point z
0
if
it has poles of arbitrarily high order which cannot be eliminated by multi-
plication by z ÿ z
0
n
, which for any ®nite choice of n. An example is the
function f ze
1=zÿ2
, which has an essential singularity at z 2.
(6) Singularities at in®nity: The singularity of f z at z 1is the same type as
that of f 1=w at w 0. For example, f zz
2
has a pole of order 2 at
z 1, since f 1=ww
ÿ2
has a pole of order 2 at w 0.
248
FUNCTIONS OF A COMPLEX VARIABLE

Elementary functions of z
The exponential function e
z
(or exp(z))
The exponential function is of fundamental importance, not only for its own sake,
but also as a basis for de®ning all the other elementary functions. In its de®nitio n
we seek to preserve as many of the characteristic properties of the real exponential
function e
x
as possible. Speci®cally, we desire that:
(a) e
z
is single-valued and analytic.
(b) de
z
=dz e
z
.
(c) e
z
reduces to e
x
when Im z 0:
Recall that if we approach the point z along the x-axis (that is, y 0;
x ! 0), the derivative of an analytic function f
0
z can be written in the form
f
0
z
df
dz
@u
@x
i
@v
@x
:
If we let
e
z
u iv;
then to satisfy (b) we must have
@u
@x
i
@v
@x
u iv:
Equating real and imaginary parts gives
@u
@x
u; 6:13
@v
@x
v: 6:14
Eq. (6.13) will be satis®ed if we write
u e
x
y; 6:15
where y is any function of y. Moreover, since e
z
is to be analytic, u and v must
satisfy the Cauchy±Riemann equations (6.11). Then using the second of Eqs.
(6.11), Eq. (6.14) becomes
ÿ
@u
@y
v:
249
ELEMENTARY FUNCTIONS OF z
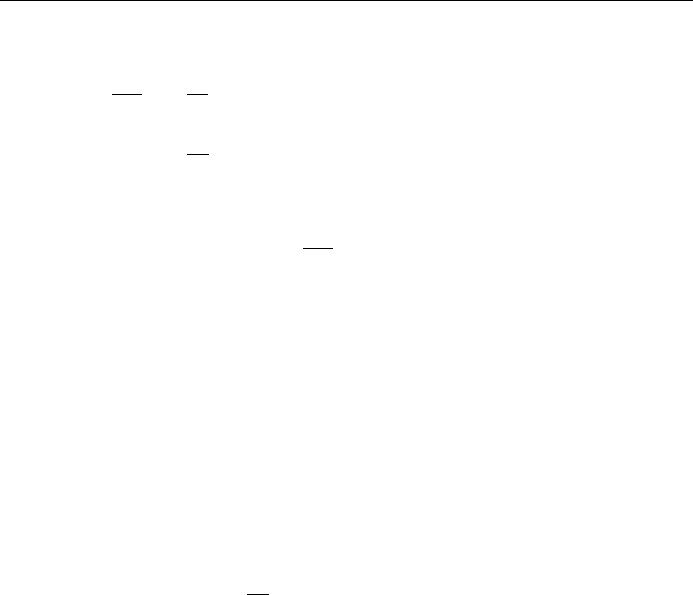
Diÿerentiating this with respect to y, we obtain
@
2
u
@y
2
ÿ
@v
@y
ÿ
@u
@x
with the aid of the first of Eqs: 6:11:
Finally, using Eq. (6.13), this becomes
@
2
u
@y
2
ÿu;
which, on substituting Eq. (6.15), becomes
e
x
00
yÿe
x
y or
00
yÿy:
This is a simple linear diÿerential equation whose solution is of the form
yA cos y B sin y:
Then
u e
x
y
e
x
A cos y B sin y
and
v ÿ
@u
@y
ÿe
x
ÿA sin y B cos y:
Therefore
e
z
u iv e
x
A cos y B sin yiA sin y ÿ B cos y:
If this is to reduce to e
x
when y 0, according to (c), we must have
e
x
e
x
A ÿ iB
from which we ®nd
A 1 and B 0:
Finally we ®nd
e
z
e
xiy
e
x
cos y i sin y: 6:16
This expression meets our requirements (a), (b), and (c); hence we adopt it as the
de®nition of e
z
. It is analytic at each point in the entire z plane, so it is an entire
function. Moreover, it satis®es the relation
e
z
1
e
z
2
e
z
1
z
2
: 6:17
It is important to note that the right hand side of Eq. (6.16) is in standard pol ar
form with the modulus of e
z
given by e
x
and an argument by y:
mod e
z
je
z
je
x
and arg e
z
y:
250
FUNCTIONS OF A COMPLEX VARIABLE
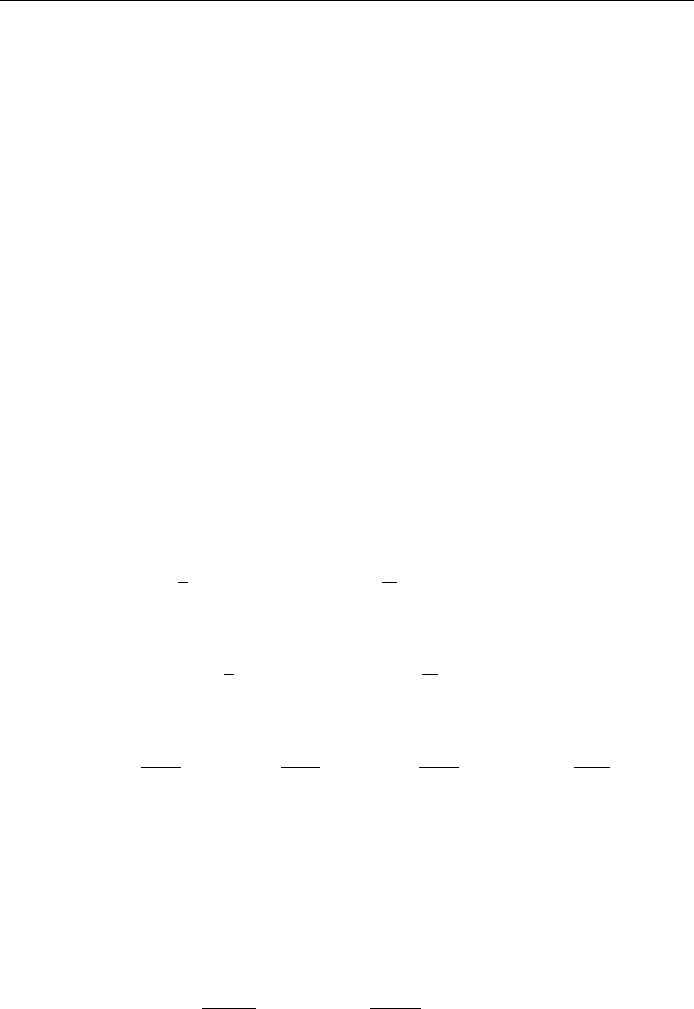
From Eq. (6.16) we obtain the Euler formula: e
iy
cos y i sin y. Now let
y 2, and since cos 2 1 and sin 2 0, the Euler formula gives
e
2i
1:
Similarly,
e
i
ÿ1; e
i=2
i:
Combining this with Eq. (6.17), we ®nd
e
z2i
e
z
e
2i
e
z
;
which shows that e
z
is periodic with the imaginary period 2i. Thus
e
z2nI
e
z
n 0; 1; 2; ...: 6:18
Because of the periodicity all the values that w f ze
z
can assume are already
assumed in the strip ÿ<y . This in®nite strip is called the fundamental
region of e
z
.
Trigonometric and hyperbolic functions
From the Euler formula we obtain
cos x
1
2
e
ix
e
ÿix
; sin x
1
2i
e
ix
ÿ e
ÿix
x real:
This suggests the following de®nitions for complex z:
cos z
1
2
e
iz
e
ÿiz
; sin z
1
2i
e
iz
ÿ e
ÿiz
: 6:19
The other trigonometric functions are de®ned in the usual way:
tan z
sin z
cos z
; cot z
cos z
sin z
; sec z
1
cos z
; cosec z
1
sin z
;
whenever the denominators are not zero.
From these de®nitions it is easy to establish the validity of such familiar for-
mulas as:
sinÿzÿsin z; cosÿzcos z; and cos
2
z sin
2
z 1;
cosz
1
z
2
cos z
1
cos z
2
þ sin z
1
sin z
2
; sinz
1
z
2
sin z
1
cos z
2
cos z
1
sin z
2
d cos z
dz
ÿsin z;
d sin z
dz
cos z:
Since e
z
is analytic for all z, the same is true for the function sin z and cos z. The
functions tan z and sec z are analytic except at the points where cos z is zero,
and cot z and cosec z are analytic except at the points where sin z is zero. The
251
ELEMENTARY FUNCTIONS OF z

functions cos z and sec z are even, and the other functions are odd. Since the
exponential function is periodic, the trigonometric functions are also periodic,
and we have
cosz 2ncos z; sinz 2nsin z;
tanz 2ntan z; cotz 2ncot z;
where n 0; 1; ...:
Another important property also carries over: sin z and cos z have the same
zeros as the corresponding real-valued functions:
sin z 0 if and only if z n n integer;
cos z 0 if and only if z 2n 1 =2 n integer:
We can also write these functions in the form ux; yivx; y. As an example,
we give the details for cos z. From Eq. (6.19) we have
cos z
1
2
e
iz
e
ÿiz
1
2
e
ixiy
e
ÿixiy
1
2
e
ÿy
e
ix
e
y
e
ÿix
1
2
e
ÿy
cos x i sin xe
y
cos x ÿ i sin x
cos x
e
y
e
ÿy
2
ÿ i sin x
e
y
ÿ e
ÿy
2
or, using the de®nitions of the hyperbolic functions of real variables
cos z cosx iycos x cosh y ÿ i sin x sinh y;
similarly,
sin z sinx iysin x cosh y i cos x sinh y:
In particular , taking x 0 in these last two formulas, we ®nd
cosiycosh y; siniyi sinh y:
There is a big diÿerence between the complex and real sine and cosine func-
tions. The real functions are bounded between ÿ1and1, but the
complex functions can take on arbitrarily large values. For example, if y is real,
then cos iy
1
2
e
ÿy
e
y
!1as y !1or y !ÿ1.
The logarithmic function w ln z
The real natural logarithm y ln x is de®ned as the inverse of the exponential
function e
y
x. For the complex logarithm, we take the same approach and
de®ne w ln z which is taken to mean that
e
w
z 6:20
for each z 6 0.
252
FUNCTIONS OF A COMPLEX VARIABLE

Setting w u iv and z re
i
jzje
i
we have
e
w
e
uiv
e
u
e
iv
re
i
:
It follows that
e
u
r z
jj
or u ln r ln z
jj
and
v arg z:
Therefore
w ln z ln r i ln zjji arg z:
Since the argument of z is determined only in multiples of 2, the complex
natural logarithm is in®nitely many-valued. If we let
1
be the principal argument
of z, that is, the particular argument of z which lies in the interval 0 <2,
then we can rewrite the last equation in the form
ln z ln z
jj
i 2n n 0; 1; 2; ...: 6:21
For any particular value of n, a unique branch of the function is determined, and
the logarithm becomes eÿectively single-valued. If n 0, the resulting branch of
the logarithmic function is called the principal value. Any particular branch of the
logarithmic function is analytic, for we have by diÿerentiating the de®nitive rela-
tion z e
w
,
dz=dw e
w
z or dw=dz dln z=dz 1=z:
For a particular value of n the deriva tive of ln z thus exists for all z 6 0.
For the real logarithm, y ln x makes sense when x > 0. Now we can take a
natural logarithm of a negative number, as shown in the following example.
Example 6.10
ln ÿ4 lnjÿ4ji argÿ4ln 4 i 2n; its principal value is ln 4 i,
a complex number. This explains why the logarithm of a negative number makes
no sense in real variable.
Hyperbolic functions
We conclude this section on ``elementary functions'' by mentioning brie¯y the
hyperbolic functions; they are de®ned at points where the denominator does not
vanish:
sinh z
1
2
e
z
ÿ e
ÿz
; cosh z
1
2
e
z
e
ÿz
;
tanh z sinh z=cosh z; coth z cosh z=sinh z;
sech z 1=cosh z; cosech z 1=sinh z:
253
ELEMENTARY FUNCTIONS OF z

Since e
z
and e
ÿz
are entire functions, sinh z and cosh z are also entire functions.
The singularities of tanh z and sech z occur at the zeros of cosh z, and the
singularities of coth z and cosech z occur at the zeros of sinh z.
As with the trigonometric functions, basic identities and derivative formulas
carry over in the same form to the complex hyperbolic functions (just replace x
by z). Hence we shall not list them here.
Complex integration
Complex integration is very important. For example, in applications we often en-
counter real integrals which cannot be evaluated by the usual methods, but we can
get help and relief from complex integration. In theory, the method of complex
integration yields proofs of some basic properties of analytic functions, which
would be very dicult to prove without using complex integration.
The most fundamental result in complex integration is Cauchy's integral theo-
rem, from which the important Cauchy integral formula follows. These will be the
subject of this section.
Line integrals in the complex plane
As in real integrals, the inde®nite integral
R
f zdz stands for any function whose
derivative is f z. The de®nite integral of real calculus is now replaced by integrals
of a complex function along a curve. Why? To see this, we can express z in terms
of a real parameter t: ztxtiyt, where, say, a t b. Now as t varies
from a to b, the point (x; y) describes a curve in the plane. We say this curve is
smooth if there exist s a tangent vector at all poin ts on the curve; this mean s that
dx/dt and dy/dt are continuous and do not vanish simultaneously for a < t < b.
Let C be such a smooth curve in the complex z plane (Fig. 6.6), and we shall
assume that C has a ®nite length (mathematicians call C a recti®able curve). Let
f z be continuous at all points of C. Subdivide C into n parts by means of points
z
1
; z
2
; ...; z
nÿ1
, chosen arbitrarily, and let a z
0
; b z
n
. On each arc joining z
kÿ1
to z
k
(k 1; 2; ...; n) choose a point w
k
(possibly w
k
z
kÿ1
or w
k
z
k
) and form
the sum
S
n
X
n
k1
f w
k
z
k
z
k
z
k
ÿ z
kÿ1
:
Now let the number of subdivisions n increase in such a way that the largest of the
chord lengths jz
k
j approaches zero. Then the sum S
n
approaches a limit. If this
limit exists and has the same value no matter how the z
j
s and w
j
s are chosen, then
254
FUNCTIONS OF A COMPLEX VARIABLE

this limit is called the integral of f z along C and is denoted by
Z
C
f zdz or
Z
b
a
f zdz: 6:22
This is often called a contour integral (with contour C) or a line integ ral of f z.
Some authors reserve the name contour integral for the special case in which C is
a closed curve (so end a and end b coincide), and denote it by the symbol
H
f zdz.
We now state, without proof, a basic theorem regarding the existence of the
contour integral: If C is piecewise smooth and f(z) is continuous on C, then
R
C
f zdz exists.
If f zux; yivx; y, the complex line integral can be expressed in terms
of real line integrals as
Z
C
f zdz
Z
C
u ivdx idy
Z
C
udx ÿ vdyi
Z
C
vdx udy; 6:23
where curve C may be open or closed but the direction of integration must be
speci®ed in eithe r case. Reversing the direction of integration results in the change
of sign of the integral. Complex integrals are, therefore, reducible to curvilinear
real integrals and possess the following properties:
(1)
R
C
f zgzdz
R
C
f zdz
R
C
gzdz;
(2)
R
C
kf zdz k
R
C
f zdz, k any constant (real or complex);
(3)
R
b
a
f zdz ÿ
R
a
b
f zdz;
(4)
R
b
a
f zdz
R
m
a
f zd
R
b
m
f zdz;
(5) j
R
C
f zdzjML, where M max jf zj on C, and L is the lengt h of C.
Property (5) is very useful, because in working with complex line integrals it is
often necessary to establish bounds on their absolute values. We now give a brief
255
COMPLEX INTEGRATION
Figure 6.6. Complex line integral.
