Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


proof. Let us go back to the de®nition:
Z
C
f zdz lim
n!1
X
n
k1
f w
k
z
k
:
Now
X
n
k1
f w
k
z
k
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
X
n
k1
f w
k
jj
z
k
jj
M
X
n
k1
z
k
jj
ML;
where we ha ve used the fact that jf zj M for all points z on C and that
P
jz
k
j repres ents the sum of all the chord lengths joining z
kÿ1
and z
k
, and
that this sum is not greater than the length L of C. Now taking the limit of
both sides, and property (5) follows. It is possible to show, more generally, that
Z
C
f zdz
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
Z
C
f z
jj
dz
jj
: 6:24
Example 6.11
Evaluate the integral
R
C
z*
2
dz, where C is a straight line joining the points z 0
and z 1 2i.
Solution: Since
z*
2
x ÿ iy
2
x
2
ÿ y
2
ÿ 2xyi;
we have
Z
C
z*
2
dz
Z
C
x
2
ÿ y
2
dx 2xydyi
Z
C
ÿ2xydx x
2
ÿ y
2
dy:
But the Cartesian equation of C is y 2x, and the above integral therefore
becomes
Z
C
z*
2
dz
Z
1
0
5x
2
dx i
Z
1
0
ÿ10x
2
dx 5=3 ÿ i10=3:
Example 6.12
Evaluate the integral
Z
C
dz
z ÿ z
0
n1
;
where C is a circle of radius r and center at z
0
, and n is an integer.
256
FUNCTIONS OF A COMPLEX VARIABLE
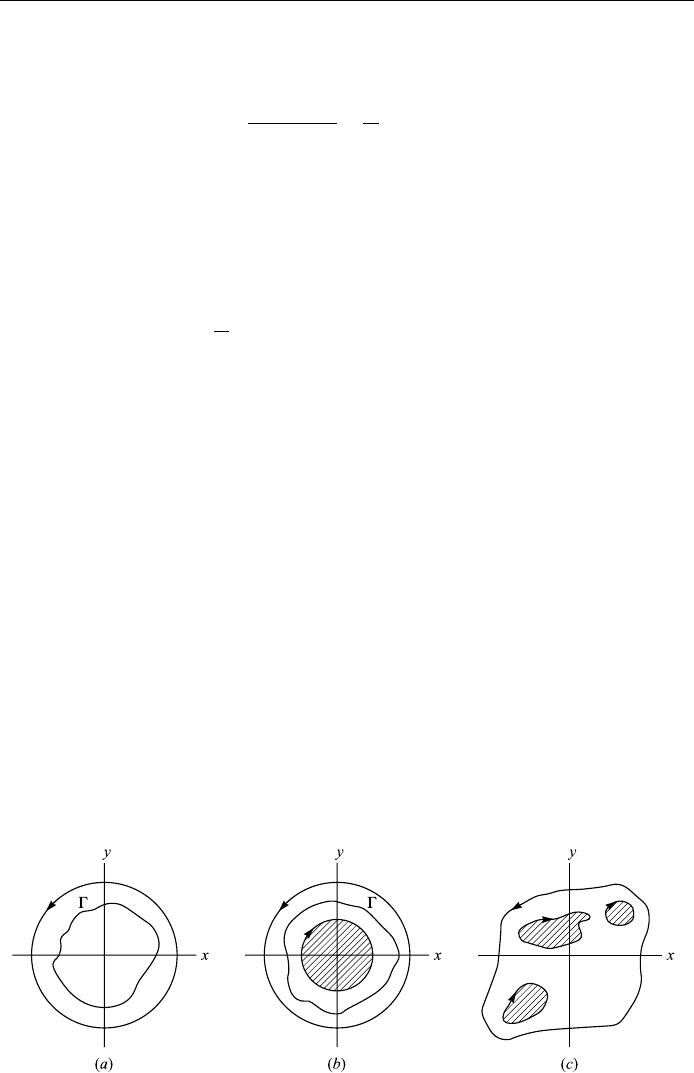
Solution: For convenience, let z ÿ z
0
re
i
, where ranges from 0 to 2 as z
ranges around the circle (Fig. 6.7). Then dz rie
i
d, and the integral becomes
Z
2
0
rie
i
d
r
n1
e
in1
i
r
n
Z
2
0
e
ÿin
d:
If n 0, this reduces to
i
Z
2
0
d 2i
and if n 6 0, we have
i
r
n
Z
2
0
cos n ÿ i sin nd 0:
This is an important and useful result to which we will refer later.
Cauchy's integral theorem
Cauchy's integral theorem has various theoretical and practical consequences. It
states that if f z is analytic in a simply-connected region (domain) an d on its
boundary C, then
I
C
f zdz 0: 6:25
What do we mean by a simply-connected region? A region R (mathematicians
prefer the term `domain') is called simply-connected if any simple closed curve
which lies in R can be shrunk to a point without leaving R. That is, a simply-
connected region has no hol e in it (Fig. 6.7(a)); this is not true for a multiply-
connected region. The multiply-connected regions of Fig. 6.7(b) and (c)have
respectively one and three holes in them.
257
COMPLEX INTEGRATION
Figure 6.7. Simply-connected and doubly-connected regions.

Although a rigorous proof of Cauchy 's integral theorem is quite demanding
and beyond the scope of this book, we shall sketch the main ideas. Note that the
integral can be expressed in terms of two-dimensional vector ®elds A and B:
I
C
f zdz
I
C
udx ÿ vdyi
Z
C
vdx udy
I
C
Ardr i
I
C
Brdr;
where
Aru
^
e
1
ÿ v
^
e
2
; Brv
^
e
1
u
^
e
2
:
Applying Stokes' theorem, we obtain
I
C
f zdz
ZZ
R
da rA irB
ZZ
R
dxdy ÿ
@v
@x
@u
@y
i
@u
@x
ÿ
@v
@y
;
where R is the region enclosed by C. Since f x satis®es the Cauchy±Riemann
conditions, both the real and the imaginary parts of the integ ral are zero, thus
proving Cauchy's integral theorem.
Cauchy's theorem is also valid for multiply-connected regions. For simplicity
we consider a doubly-connected region (Fig. 6.8). f z is analytic in and on the
boundary of the region R between two simple closed curves C
1
and C
2
. Construct
a cross-cut AF. Then the region bounded by ABDEAFGHFA is simply-connected
so by Cauchy's theorem
I
C
f zdz
I
ABDEAFGHFA
f zdz 0
or
Z
ABDEA
f zdz
Z
AF
f zdz
Z
FGHF
f zdz
Z
FA
f zdz 0:
258
FUNCTIONS OF A COMPLEX VARIABLE
Figure 6.8. Proof of Cauchy's theorem for a doubly-connected region.

But
R
AF
f zdz ÿ
R
FA
f zdz, therefore this becomes
Z
ABDEA
f zdzy
Z
FGHF
f zdzy 0
or
I
C
f zdz
I
C
1
f zdz
I
C
2
f zdz 0; 6:26
where both C
1
and C
2
are traversed in the positive direction (in the sense that an
observer walking on the boundary always has the region R on his left). Note that
curves C
1
and C
2
are in opposite directions.
If we reverse the direction of C
2
(now C
2
is also counterclockwise, that is, both
C
1
and C
2
are in the same direction.), we have
I
C
1
f zdz ÿ
I
C
2
f zdz 0or
I
C
2
f zdz
I
C
1
f zdz:
Because of Cauchy's theorem, an integration contour can be moved across any
region of the complex plane over whi ch the integrand is analytic without changing
the value of the integral. It cannot be moved across a hole (the shaded area) or a
singularity (the dot), but it can be made to collapse around one, as shown in Fig.
6.9. As a result, an integration contour C enclosing n holes or singularities can be
replaced by n separated closed contours C
i
, each enclosing a hole or a singularity:
I
C
f zdz
X
n
k1
I
C
i
f zdz
which is a generalization of Eq. (6.26) to multiply-connected regions .
There is a converse of the Cauchy's theorem, known as Morera's theorem. We
now state it without proof:
Morera's theorem:
If f(z) is continuous in a simply-connected region R and the Cauchy's theorem is
valid around every simple closed curve C in R, then f z is analytic in R.
259
COMPLEX INTEGRATION
Figure 6.9. Collapsing a contour around a hole and a singularity.

Example 6.13
Evaluate
H
C
dz=z ÿ a where C is any simple closed curve and z a is (a) outside
C,(b) inside C.
Solution: (a)Ifa is outside C, then f z1=z ÿ a is analytic everywhere inside
and on C. Hence by Cauchy's theorem
I
C
dz=z ÿ a0:
(b)Ifa is inside C and ÿ is a circle of radius 2 with center at z a so that ÿ is
inside C (Fig. 6.10). Then by Eq. (6.26) we have
I
C
dz=z ÿ a
I
ÿ
dz=z ÿ a:
Now on ÿ, jz ÿ aj",orz ÿ a "e
i
, then dz i"e
i
d, and
I
ÿ
dz
z ÿ a
Z
2
0
i"e
i
d
"e
i
i
Z
2
0
d 2i:
Cauchy's integral formulas
One of the most important consequences of Cauchy's integral theorem is what is
known as Cauchy's integral formula. It may be stated as follows.
If f(z) is analytic in a simply-connected regio n R, and z
0
is any
point in the interior of R which is enclosed by a simple closed curve
C, then
f z
0
1
2i
I
C
f z
z ÿ z
0
dz; 6:27
the integration around C being taken in the positive sense (counter-
clockwise).
260
FUNCTIONS OF A COMPLEX VARIABLE
Figure 6.10.
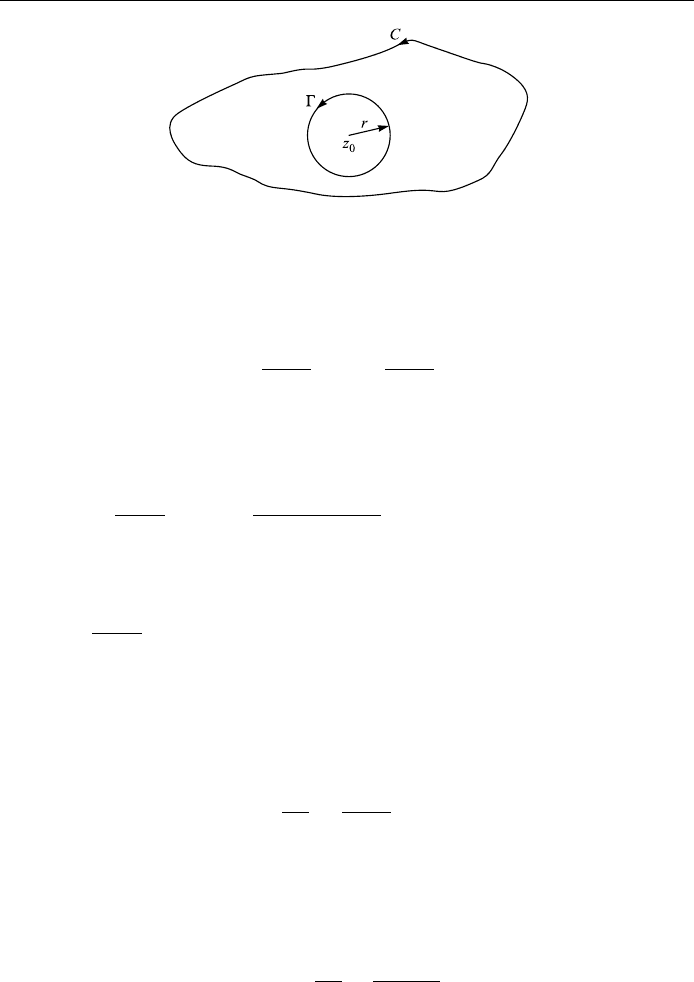
To prove this, let ÿ be a small circle with center at z
0
and radius r (Fig. 6.11),
then by Eq. (6.26) we have
I
C
f z
z ÿ z
0
dz
I
ÿ
f z
z ÿ z
0
dz:
Now jz ÿ z
0
jr or z ÿ z
0
re
i
; 0 <2. Then dz ire
i
d and the integral
on the right becomes
I
ÿ
f z
z ÿ z
0
dz
Z
2
0
f z
0
re
i
ire
i
re
i
d i
Z
2
0
f z
0
re
i
d:
Taking the limit of both sides and making use of the continuity of f z,wehave
I
C
f z
z ÿ z
0
dz lim
r!0
Z
2
0
f z
0
re
i
d
i
Z
2
0
lim
r!0
f z
0
re
i
d i
Z
2
0
f z
0
d 2if z
0
;
from which we obtain
f z
0
1
2i
I
C
f z
z ÿ z
0
dz q:e:d:
Cauchy's integral formula is also true for multiply-connected regions, but we shall
leave its proof as an exercise.
It is useful to write Cauchy's integral formula (6.27) in the form
f z
1
2i
I
C
f z
0
dz
0
z
0
ÿ z
to emphasi ze the fact that z can be any point inside the close curve C.
Cauchy's integral formula is very useful in evaluating integrals, as shown in the
following example.
261
COMPLEX INTEGRATION
Figure 6.11. Cauchy's integral formula.

Example 6.14
Evaluate the integral
H
C
e
z
dz=z
2
1 ,ifC is a circle of unit radius with center at
(a) z i and (b) z ÿi.
Solution: (a) We ®rst rewrite the integral in the form
I
C
e
z
z i
dz
z ÿ i
;
then we see that f ze
z
=z i and z
0
i. Moreover, the function f z is
analytic everyw here within and on the given circle of unit radius around z i.
By Cauchy's integral formula we have
I
C
e
z
z i
dz
z ÿ i
2if i2i
e
i
2i
cos 1 i sin 1:
(b) We ®nd z
0
ÿi and f ze
z
=z ÿ i . Cauchy's integral formula gives
I
C
e
z
z ÿ i
dz
z i
ÿcos 1 ÿ i sin 1:
Cauchy's integral formula for higher derivatives
Using Cauchy's integral formula, we can show that an analytic function f z has
derivatives of all orders given by the following formula:
f
n
z
0
n!
2i
I
C
f zdz
z ÿ z
0
n1
; 6:28
where C is any simple closed curve around z
0
and f z is analytic on and inside C.
Note that this formula implies that each derivative of f z is itself analytic, since it
possesses a derivative.
We now prove the formula (6.28) by induction on n. That is, we ®rst prove the
formula for n 1:
f
0
z
0
1
2i
I
C
f zdz
z ÿ z
0
2
:
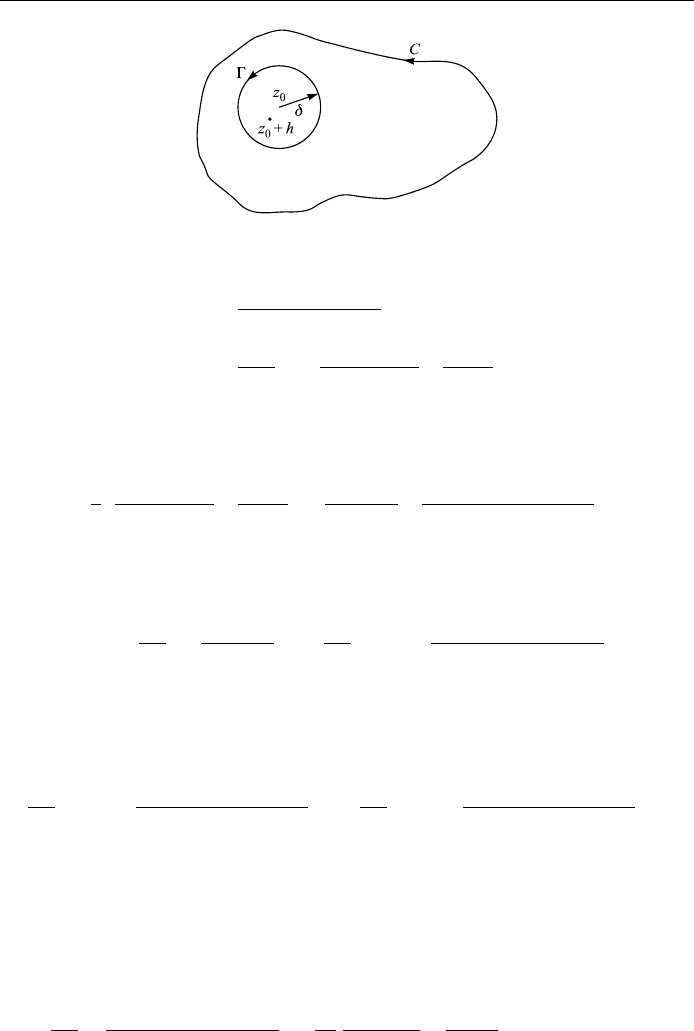
As shown in Fig. 6.12, both z
0
and z
0
h lie in R, and
f
0
z
0
lim
h!0
f z
0
hÿf z
0
h
:
Using Cauchy's integral formula we obtain
262
FUNCTIONS OF A COMPLEX VARIABLE
f
0
z
0
lim
h!0
f z
0
hÿf z
0
h
lim
h!0
1
2ih
I
C
1
z ÿz
0
h
ÿ
1
z ÿ z
0
f zdz:
Now
1
h
1
z ÿz
0
h
ÿ
1
z ÿ z
0
1
z ÿ z
0
2
h
z ÿ z
0
ÿ hz ÿ z
0
2
:
Thus,
f
0
z
0
1
2i
I
C
f z
z ÿ z
0
2
dz
1
2i
lim
h!0
h
I
C
f z
z ÿ z
0
ÿ hz ÿ z
0
2
dz:
The proof follows if the limit on the right hand side approaches zero as h ! 0. To
show this, let us draw a small circle ÿ of radius centered at z
0
(Fig. 6.12), then
1
2i
lim
h!0
h
I
C
f z
z ÿ z
0
ÿ hz ÿ z
0
2
dz
1
2i
lim
h!0
h
I
ÿ
f z
z ÿ z
0
ÿ hz ÿ z
0
2
dz:
Now choose h so small (in absolute value) that z
0
h lies in ÿ and jhj <=2,
and the equation for ÿ is jz ÿ z
0
j. Thus, we have jz ÿ z
0
ÿ hj
jz ÿ z
0
jÿjhj >ÿ =2 =2. Next, as f z is analytic in R, we can ®nd a positive
number M such that jf zj M. And the length of ÿ is 2. Thus,
h
2i
I
ÿ
f zdz
z ÿ z
0
ÿ hz ÿ z
0
2
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
h
jj
2
M2
=2
2
2 h
jj
M
2
! 0ash ! 0;
proving the formula for f
0
z
0
.
263
COMPLEX INTEGRATION
Figure 6.12.

For n 2, we begin with
f
0
z
0
hÿf
0
z
0
h
1
2ih
I
C
1
z ÿ z
0
h
2
ÿ
1
z ÿ z
0
2
()
f zdz
2!
2i
I
C
f z
z ÿ z
0
3
dz
h
2i
I
C
3z ÿ z
0
ÿ2h
z ÿ z
0
ÿ h
2
z ÿ z
0
3
f zdz:
The result follows on taking the limit as h ! 0 if the last term approaches zero.
The proof is similar to that for the case n 1, for using the fact that the integral
around C equals the integral around ÿ, we have
h
2i
I
ÿ
3z ÿ z
0
ÿ2h
z ÿ z
0
ÿ h
2
z ÿ z
0
3
f zdz
h
jj
2
M2
=2
2
3
4 h
jj
M
4
;
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
assuming M exists such that j3z ÿ z
0
ÿ2hf zj < M.
In a similar manner we can establish the results for n 3; 4; .... We leave it to
the reader to complete the proof by establishing the formula for f
n1
z
0
, assum-
ing that f
n
z
0
is true.
Sometimes Cauchy's integral formula for highe r derivatives can be used to
evaluate integ rals, as illustrated by the following example.
Example 6.15
Evaluate
I
C
e
2z
z 1
4
dz;
where C is any simple closed path not passing through ÿ1. Consider two cases:
(a) C does not enclose ÿ1. Then e
2z
=z 1
4
is analytic on and inside C, and the
integral is zero by Cauchy's integral theorem.
(b) C encloses ÿ1. Now Cauchy's integral formula for higher derivatives
applies.
Solution: Let f ze
2z
, then
f
3
ÿ1
3!
2i
I
C
e
2z
z 1
4
dz:
Now f
3
ÿ18e
ÿ2
, hence
I
C
e
2z
z 1
4
dz
2i
3!
f
3
ÿ1
8
3
e
ÿ2
i:
264
FUNCTIONS OF A COMPLEX VARIABLE

Series repres entations of analytic functions
We now turn to a very important notion: series representations of analytic func-
tions. As a prelude we must discuss the notion of convergence of complex series.
Most of the de®nitions and theorems relating to in®nite series of real terms can be
applied with little or no change to series whose terms are complex.
Complex sequences
A complex sequence is an ordered list which assigns to each positive integer n a
complex number z
n
:
z
1
; z
2
; ...; z
n
; ...:
The numbers z
n
are called the terms of the sequence. For example, both
i; i
2
; ...; i
n
; ... or 1 i ; 1 i=2; 1 i=4; 1 i=8; ... are complex sequences.
The nth term of the second sequence is (1 i=2
nÿ1
. A sequence
z
1
; z
2
; ...; z
n
; ... is said to be convergent with the limit l (or simply to converge
to the number l) if, g iven ">0, we can ®nd a positive integer N such that
jz
n
ÿ lj <"for each n N (Fig. 6.13). Then we write
lim
n!1
z
n
l:
In words, or geometrically, this means that each term z
n
with n > N (that is,
z
N
; z
N1
; z
N2
; ... lies in the open circular region of radius " with center at l.
In general, N depends on the choice of ". Here is an illustrative example.
Example 6.17
Using the de®nition, show that lim
n!1
1 z=n1 for all z.
265
SERIES REPRESENTATIONS OF ANALYTIC FUNCTIONS
Figure 6.13. Convergent complex sequence.
