Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


7
Special functions of
mathematical physics
The functions discussed in this chapter arise as solutions of second-order diÿer-
ential equations which appear in special, rather than in general, physical pro-
blems. So these functions are usually known as the special functions of
mathematical physics. We start with Legendre's equation (Adrien Marie
Legendre, 1752±1833, French mathematician).
Legendre's equation
Legendre's diÿerential equation
1 ÿ x
2
d
2
y
dx
2
ÿ 2x
dy
dx
1y 0; 7:1
where v is a positive constant, is of great impor tance in classical and quantum
physics. The reader will see this equation in the study of central force motion in
quantum mechanics. In general, Legendre's equation appears in problems in
classical mechanics, electromagnetic theory, heat, and qua ntum mechanics, with
spherical symmetry.
Dividing Eq. (7.1) by 1 ÿ x
2
, we obtain the standard form
d
2
y
dx
2
ÿ
2x
1 ÿ x
2
dy
dx
1
1 ÿ x
2
y 0 :
We see that the coecients of the resulting equation are analytic at x 0, so the
origin is an ordinary point and we may write the series solution in the form
y
X
1
m0
a
m
x
m
: 7:2
296

Substituting this and its derivatives into Eq. (7.1) and denoting the constant
1 by k we obtain
1 ÿ x
2
X
1
m2
mm ÿ 1a
m
x
mÿ2
ÿ 2x
X
1
m1
ma
m
x
mÿ1
k
X
1
m0
a
m
x
m
0:
By writing the ®rst term as two separate series we have
X
1
m2
mm ÿ 1a
m
x
mÿ2
ÿ
X
1
m2
mm ÿ 1a
m
x
m
ÿ 2
X
1
m1
ma
m
x
m
k
X
1
m0
a
m
x
m
0;
which can be written as:
2 1a
2
3 2a
3
x 4 3a
4
x
2
s 2s 1a
s2
x
s
ÿ2 1a
2
x
2
ÿ ÿss ÿ 1a
s
x
s
ÿ
ÿ2 1a
1
x ÿ 2 2a
2
x
2
ÿ ÿ2sa
s
x
s
ÿ
ka
0
ka
1
x ka
2
x
2
ka
s
x
s
0:
Since this must be an identity in x if Eq. (7.2) is to be a solution of Eq. (7.1), the
sum of the coecients of each power of x must be zero; remembering that
k 1 we thus have
2a
2
1a
0
0; 7:3a
6a3 ÿ2 vv 1a
1
0; 7:3b
and in general, when s 2; 3; ...;
s 2s 1a
s2
ÿss ÿ 1ÿ2s 1a
s
0: 4:4
The expression in square brackets [...] can be written
ÿ s s 1:
We thus obtain from Eq. (7.4)
a
s2
ÿ
ÿ s s 1
s 2 s 1
a
s
s 0; 1; ...: 7:5
This is a recursion formula, giving each coecient in terms of the one two places
before it in the series, except for a
0
and a
1
, which are left as arbitrary constants.
297
LEGENDRE'S EQUATION

We ®nd successively
a
2
ÿ
1
2!
a
0
; a
3
ÿ
ÿ 1 2
3!
a
1
;
a
4
ÿ
ÿ 2 3
4 3
a
2
; a
5
ÿ
ÿ 3 4
3!
a
3
;
ÿ 2 1 3
4!
a
0
;
ÿ 3 ÿ 1 2 4
5!
a
1
;
etc. By inserting these values for the coecients into Eq. (7.2) we obtain
yxa
0
y
1
xa
1
y
2
x; 7:6
where
y
1
x1 ÿ
1
2!
x
2
ÿ 2 1 3
4!
x
4
ÿ 7:7a
and
y
2
xx
ÿ 1 2
3!
x
3
ÿ 2 ÿ 1 2 4
5!
x
5
ÿ: 7:7b
These series converge for jxj < 1. Since Eq. (7.7a) contains even powers of x, and
Eq. (7.7b) contains odd powers of x, the ratio y
1
=y
2
is not a constant, and y
1
and
y
2
are linearly independent solutions. Hence Eq. (7.6) is a general solution of Eq.
(7.1) on the interval ÿ1 < x < 1.
In many applications the parameter in Legendre's equation is a positive
integer n. Then the right hand side of Eq. (7.5) is zero when s n and, therefore,
a
n2
0 and a
n4
0; ...: Hence, if n is even, y
1
x reduces to a polynomial of
degree n.Ifn is odd, the same is true with respect to y
2
x. These polynomials,
multiplied by some constants, are called Legendre polynomials. Since they are of
great practical importance, we will consider them in some detail. For this purpose
we rewrite Eq. (7.5 ) in the form
a
s
ÿ
s 2s 1
nÿsn s 1
a
s2
7:8
and then express all the non-vanishing coecients in terms of the coecient a
n
of
the highest power of x of the polynomial. The coecient a
n
is then arbitrary. It is
customary to choose a
n
1 when n 0 and
a
n
2n!
2
n
n!
2
1 3 5 2n ÿ 1
n!
; n 1 ; 2; ...; 7:9
298
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS
the reason being that for this choice of a
n
all those polynomials will have the value
1 when x 1. We then obtain from Eqs. (7.8) and (7.9)
a
nÿ2
ÿ
nn ÿ 1
22n ÿ 1
a
n
ÿ
nn ÿ 12n!
22n ÿ 12
n
n!
2
ÿ
nn ÿ 12n2n ÿ 12n ÿ 2!!
22n ÿ 12
n
nn ÿ 1!nn ÿ 1n ÿ 2!
;
that is,
a
nÿ2
ÿ
2n ÿ 2!
2
n
n ÿ 1!n ÿ 2!
:
Similarly,
a
nÿ4
ÿ
n ÿ 2n ÿ 3
42n ÿ 3
a
nÿ2
2n ÿ 4!
2
n
2!n ÿ 2!n ÿ 4!
etc., and in general
a
nÿ2m
ÿ1
m
2n ÿ 2m!
2
n
m!n ÿ m!n ÿ 2m!
: 7:10
The resulting solution of Legendre's equation is called the Legendre polynomial
of degree n and is denoted by P
n
x; from Eq. (7.10) we obtain
P
n
x
X
M
m0
ÿ1
m
2n ÿ 2m!
2
n
m!n ÿ m!n ÿ 2m!
x
nÿ2m
2n!
2
n
n!
2
x
n
ÿ
2n ÿ 2!
2
n
1!n ÿ 1!n ÿ 2!
x
nÿ2
ÿ;
7:11
where M n=2orn ÿ 1=2, whichever is an integer. In particular (Fig. 7.1)
P
0
x1; P
1
xx; P
2
x
1
2
3x
2
ÿ 1; P
3
x
1
2
5x
3
ÿ 3x;
P
4
x
1
8
35x
4
ÿ 30x
2
3 ; P
5
x
1
8
63x
5
ÿ 70x
3
15x:
Rodrigues' formula for P
n
x
The Legendre polynomials P
n
x are given by the formula
P
n
x
1
2
n
n!
d
n
dx
n
x
2
ÿ 1
n
: 7:12
We shall establish this result by actually carrying out the indicated diÿerentia-
tions, using the Leibnitz rule for nth derivative of a product, which we state below
without proof:
299
LEGENDRE'S EQUATION
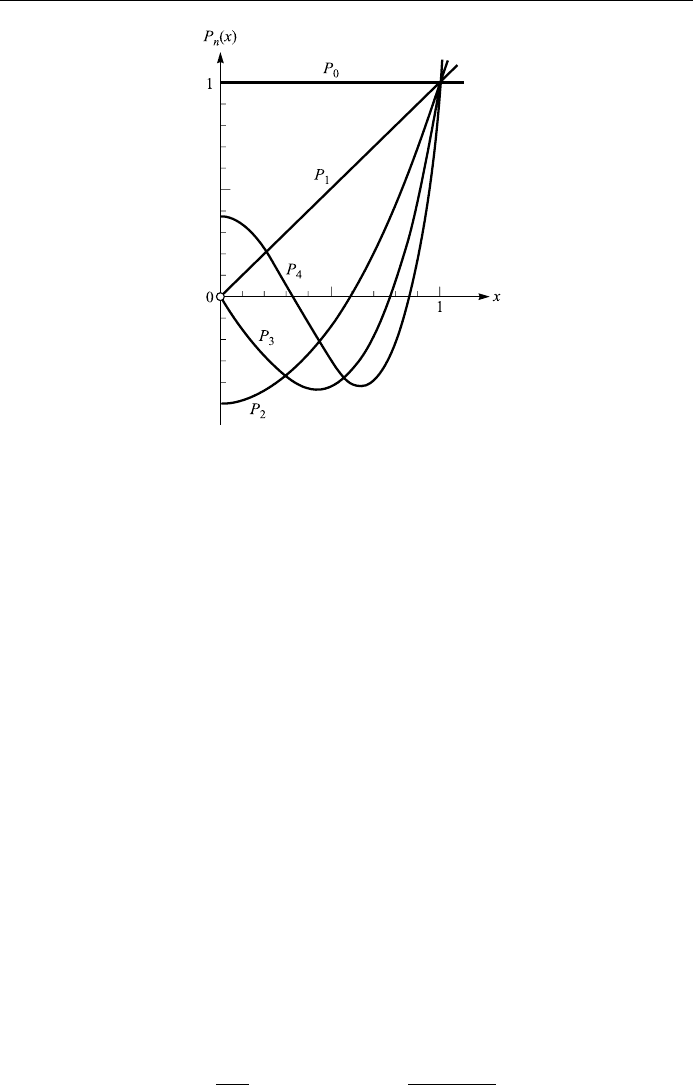
If we write D
n
u as u
n
and D
n
v as v
n
, then
uv
n
uv
n
n
C
1
u
1
v
nÿ1
n
C
r
u
r
v
nÿr
u
n
v;
where D d=dx and
n
C
r
is the binomial coecient and is equal to n!=r!n ÿ r!.
We ®rst notice that Eq. (7.12) holds for n 0, 1. Then, write
z x
2
ÿ 1
n
=2
n
n!
so that
x
2
ÿ 1 Dz 2nxz: 7:13
Diÿerentiating Eq. (7.13) n 1 times by the Leibnitz rule, we get
1 ÿ x
2
D
n2
z ÿ 2xD
n1
z nn 1 D
n
z 0:
Writing y D
n
z, we then have:
(i) y is a polyno mial.
(ii) The coecient of x
n
in x
2
ÿ 1
n
is ÿ1
n=2 n
C
n=2
(n even) or 0 (n odd).
Therefore the lowest power of x in yx is x
0
(n even) or x
1
(n odd). It
follows that
y
n
00 n odd
and
y
n
0
1
2
n
n!
ÿ1
n=2
n
C
n=2
n!
ÿ1
n=2
n!
2
n
n=2!
2
n even:
300
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS
Figure 7.1. Legendre polynomials.

By Eq. (7.11) it follows that
y
n
0P
n
0all n:
(iii) 1 ÿ x
2
D
2
y ÿ 2xDy nn 1y 0, which is Legendre's equation.
Hence Eq. (7.12) is true for all n.
The generating function for P
n
x
One can prove that the polynomials P
n
x are the coecients of z
n
in the expan-
sion of the function x; z1 ÿ 2xz z
2
ÿ1=2
, with jzj < 1; that is,
x; z1 ÿ 2xz z
2
ÿ1=2
X
1
n0
P
n
xz
n
; z
jj
< 1: 7:14
x; z is called the generating function for Legendre polynomials P
n
x. We shall
be concerned only with the case in which
x cos ÿ<
and then
z
2
ÿ 2xz 1 z ÿ e
i
z ÿ e
i
:
The expansion (7.14) is therefore possible when jzj < 1. To prove expansion (7.14)
we have
lhs 1
1
2
z2x ÿ 1
1 3
2
2
2!
z
2
2x ÿ z
2
1 3 2n ÿ 1
2
n
n!
z
n
2x ÿ z
n
:
The coecient of z
n
in this power seri es is
1 3 2n ÿ 1
2
n
n!
2
n
x
n
1 3 2n ÿ 3
2
nÿ1
n ÿ 1!
ÿn ÿ 12x
nÿ2
P
n
x
by Eq. (7.11). We can use Eq. (7.14) to ®nd successive polynomials explicitly.
Thus, diÿerentiating Eq. (7.14) with respect to z so that
x ÿ z1 ÿ 2xz z
2
ÿ3=2
X
1
n1
nz
nÿ1
P
n
x
and using Eq. (7.14) again gives
x ÿ z P
0
x
X
1
n1
P
n
xz
n
"#
1 ÿ 2xz z
2
X
1
n1
nz
nÿ1
P
n
x: 7:15
301
LEGENDRE'S EQUATION

Then expanding coecients of z
n
in Eq. (7.15) leads to the recurrence relation
2n 1xP
n
xn 1P
n1
xnP
nÿ1
x: 7:16
This gives P
4
; P
5
; P
6
, etc. very quickly in term s of P
0
; P
1
, and P
3
.
Recurrence relations are very useful in simplifying work, helping in pro ofs
or derivations. We list four more recurrence relations below without proofs or
derivations:
xP
0
n
xÿP
0
nÿ1
xnP
n
x; 7:16a
P
0
n
xÿxP
0
nÿ1
xnP
nÿ1
x; 7:16b
1 ÿ x
2
P
0
n
xnP
nÿ1
xÿnxP
n
x; 7:16c
2n 1P
n
xP
0
n1
xÿP
0
nÿ1
x: 7:16d
With the help of the recurrence formulas (7.16) and (7.16b), it is straight-
forward to establish the other three. Omitting the full details, which are left for
the reader, these relations can be obtained as follows :
(i) diÿerentiation of Eq. (7.16) with respect to x and the use of Eq. (7.16b) to
eliminate P
0
n1
x leads to relation (7.16a);
(ii) the addition of Eqs. (7.16a) and (7.16b) immediately yields relation
(7.16d);
(iii) the elimination of P
0
nÿ1
x between Eqs. (7.16b) and (7.16a) gives relation
(7.16c).
Example 7.1
The phy sical signi®cance of expansion (7.14) is apparent in this simple example:
®nd the potential V of a point charge at point P due to a charge q at Q.
Solution: Suppose the origin is at O (Fig. 7.2). Then
V
P
q
R
q
2
ÿ 2r cos r
2
ÿ1=2
:
302
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS
Figure 7.2.

Thus, if r <
V
P
q
1 ÿ 2z cos z
2
ÿ1=2
; z r=;
which gives
V
P
q
X
1
n0
r
n
P
n
cos r <:
Similarly, when r >, we get
V
P
q
X
1
n0
r
n1
P
n
cos :
There are many problems in which it is essential that the Legendre polynomials
be expressed in terms of , the colatitude angle of the spherical coordinate system.
This can be done by replacing x by co s . But this will lead to expressions that are
quite inconvenient because of the powers of cos they contain. Fortunately, using
the generating function provided by Eq. (7.14), we can derive more useful forms in
which cosines of multiples of take the place of powers of cos . To do this, let us
substitute
x cos e
i
e
ÿi
=2
into the generating function, which gives
1 ÿ ze
i
e
ÿi
z
2
ÿ1=2
1 ÿ ze
i
1 ÿ ze
ÿi
ÿ1=2
X
1
n0
P
n
cos z
n
:
Now by the binomi al theorem, we have
1 ÿ ze
i
ÿ1=2
X
1
n0
a
n
z
n
e
ni
; 1 ÿ ze
ÿi
ÿ1=2
X
1
n0
a
n
z
n
e
ÿni
;
where
a
n
1 3 5 2n ÿ 1
2 4 6 2n
; n 1; a
0
1: 7:17
To ®nd the coecient of z
n
in the product of these two series, we need to form the
Cauchy product of these two series. What is a Cauchy product of two series? We
state it below for the reader who is in need of a review:
The Cauchy product of two in®nite series,
P
1
n0
u
n
x
and
P
1
n0
v
n
x, is de®ned as the sum over n
X
1
n0
s
n
x
X
1
n0
X
n
k0
u
k
xv
nÿk
x;
303
LEGENDRE'S EQUATION

where s
n
x is given by
s
n
x
X
n
k0
u
k
xv
nÿk
xu
0
xv
n
xu
n
xv
0
x:
Now the Cauchy pro duct for our two seri es is given by
X
1
n0
X
n
k0
a
nÿk
z
nÿk
e
nÿki
a
k
z
k
e
ÿki
X
1
n0
z
n
X
n
k0
a
k
a
nÿk
e
nÿ2ki
: 7:18
In the inner sum, which is the sum of interest to us, it is straightforward to prove
that, for n 1, the terms corresponding to k j and k n ÿ j are identical except
that the exponents on e are of opposite sign. Hence these terms can be paired, and
we have for the coecient of z
n
,
P
n
cos a
0
a
n
e
ni
e
ÿni
a
1
a
nÿ1
e
nÿ2i
e
ÿnÿ2i
2 a
0
a
n
cos n a
1
a
nÿ1
cosn ÿ 2 :
7:19
If n is odd, the number of terms is even and each has a place in one of the pairs. In
this case, the last term in the sum is
a
nÿ1=2
a
n1=2
cos :
If n is even, the number of terms is odd and the middle term is unpaired. In this
case, the series (7.19) for P
n
cos ends with the constant term
a
n=2
a
n=2
:
Using Eq. (7.17) to compute values of the a
n
, we ®nd from the unit coecient of z
0
in Eqs. (7.18) and (7.19), whet her n is odd or even, the speci®c expressions
P
0
cos 1; P
1
cos cos ; P
2
cos 3 cos 2 1=4
P
3
cos 5 cos 3 3 cos =8
P
4
cos 35 cos 4 20 cos 2 9 =64
P
5
cos 63 cos 5 35 cos 3 30 cos =128
P
6
cos 231 cos 6 126 cos 4 105 cos 2 50=512
9
>
>
>
>
>
>
>
>
=
>
>
>
>
>
>
>
>
;
: 7:20
Orthogonality of Legendre polynomials
The set of Legendre polynomials fP
n
xg is orthogonal for ÿ 1 x 1. In
particular we can show that
Z
1
ÿ1
P
n
xP
m
xdx
2=2n 1 if m n
0ifm 6 n
:
7:21
304
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS
(i) m 6 n: Let us rewrite the Legendre equation (7.1) for P
m
x in the form
d
dx
1 ÿ x
2
P
0
m
x
mm 1P
m
x0 7:22
and the one for P
n
x
d
dx
1 ÿ x
2
P
0
n
x
nn 1P
n
x0: 7:23
We then multiply Eq. (7.22) by P
n
x and Eq. (7.23) by P
m
x, and subtract to get
P
m
d
dx
1 ÿ x
2
P
0
n
ÿ P
n
d
dx
1 ÿ x
2
P
0
m
nn 1ÿmm 1P
m
P
n
0:
The ®rst two terms in the last equation can be written as
d
dx
1 ÿ x
2
P
m
P
0
n
ÿ P
n
P
0
m
:
Combining this with the last equation we have
d
dx
1 ÿ x
2
P
m
P
0
n
ÿ P
n
P
0
m
nn 1ÿmm 1P
m
P
n
0:
Integrating the above equation between ÿ1 and 1 we obtain
1 ÿ x
2
P
m
P
0
n
ÿ P
n
P
0
m
j
1
ÿ1
nn 1ÿmm 1
Z
1
ÿ1
P
m
xP
n
xdx 0:
The integrated term is zero because (1 ÿ x
2
0atx 1, and P
m
x and P
n
x
are ®nite. The bracket in front of the integral is not zero since m 6 n. Therefore
the integral must be zero and we have
Z
1
ÿ1
P
m
xP
n
xdx 0; m 6 n:
(ii) m n: We now use the recurrence relation (7.16a), namely
nP
n
xxP
0
n
xÿP
0
nÿ1
x:
Multiplying this recurrence relation by P
n
x and integrating between ÿ1 and 1,
we obtain
n
Z
1
ÿ1
P
n
x
2
dx
Z
1
ÿ1
xP
n
xP
0
n
xdx ÿ
Z
1
ÿ1
P
n
xP
0
nÿ1
xdx: 7:24
The second integral on the right hand side is zero. (Why?) To evaluate the ®rst
integral on the right hand side, we integrate by parts
Z
1
ÿ1
xP
n
xP
0
n
xdx
x
2
P
n
x
2
j
1
ÿ1
ÿ
1
2
Z
1
ÿ1
P
n
x
2
dx 1 ÿ
1
2
Z
1
ÿ1
P
n
x
2
dx:
305
LEGENDRE'S EQUATION
