Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


to the last factor. Then
f z
1
2i
I
C
1
f w
w ÿ a
1
z ÿ a
w ÿ a
z ÿ a
w ÿ a
nÿ1
z ÿ a
n
=w ÿ a
n
1 ÿz ÿ a=w ÿ a
dw
1
2i
I
C
2
f w
z ÿ a
1
w ÿ a
z ÿ a
w ÿ a
z ÿ a
nÿ1
w ÿ a
n
=z ÿ a
n
1 ÿw ÿ a=z ÿ a
dw
1
2i
I
C
1
f wdw
w ÿ a
z ÿ a
2i
I
C
2
f wdw
w ÿ a
2
z ÿ a
nÿ1
2i
I
C
2
f wdw
w ÿ a
n
R
n1
1
2iz ÿ a
I
C
2
f wdw
1
2iz ÿ a
2
I
C
1
w ÿ af wdw
1
2iz ÿ a
n
I
C
1
w ÿ a
nÿ1
f wdw R
n2
;
where
R
n1
z ÿ a
n
2i
I
C
1
f wdw
w ÿ a
n
w ÿ z
;
R
n2
1
2iz ÿ a
n
I
C
2
w ÿ a
n
f wdw
z ÿ w
:
The theorem will be established if we can show that lim
n!1
R
n2
0
and lim
n!1
R
n1
0. The proof of lim
n!1
R
n1
0 has already been given in the
derivation of the Taylor series. To prove the second limit, we note that for values
of w on C
2
jw ÿ ajr
1
; jz ÿ aj say; jz ÿ wjjz ÿ aÿw ÿ aj ÿ r
1
;
and
jf wj M;
where M is the maximum of jf wj on C
2
. Thus
R
n
2
ÿ
ÿ
ÿ
ÿ
1
2iz ÿ a
n
I
C
2
w ÿ a
n
f wdw
z ÿ w
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
1
2i
jj
z ÿ a
jj
n
I
C
2
w ÿ a
jj
n
f w
jj
dw
jj
z ÿ w
jj
or
R
n
2
ÿ
ÿ
ÿ
ÿ
r
n
1
M
2
n
ÿ r
1
I
C
2
dw
jj
M
2
r
1
n
2r
1
ÿ r
1
:
276
FUNCTIONS OF A COMPLEX VARIABLE
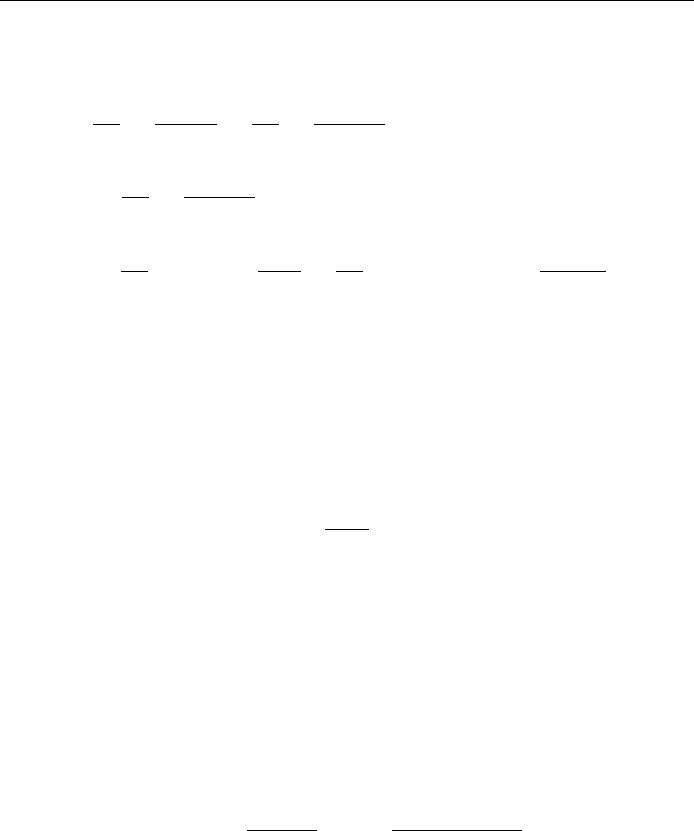
Since r
1
= < 1, the last expression approaches zero as n !1. Hence
lim
n!1
R
n2
0 and we have
f z
1
2i
I
C
1
f wdw
w ÿ a
1
2i
I
C
1
f wdw
w ÿ a
2
"#
z ÿ a
1
2i
I
C
1
f wdw
w ÿ a
3
"#
z ÿ a
2
1
2i
I
C
2
f wdw
1
z ÿ a
1
2i
I
C
2
w ÿ af wdw
1
z ÿ a
2
:
Since f z is analytic throughout the region between C
1
and C
2
, the paths of
integration C
1
and C
2
can be replaced by any other curve C within this region
and enclosing C
2
. And the resulting integrals are precisely the coecients a
n
given
by Eq. (6.35). This proves the Laurent theorem.
It should be noted that the coecients of the positive powers (z ÿ a) in the
Laurent expan sion, while identical in form with the integrals of Eq. (6.28), cannot
be replaced by the derivative expressions
f
n
a
n!
as they were in the derivation of Taylor series, since f z is not analytic through-
out the entire interior of C
2
(or C), and hence Cauchy's generalized integral
formula cannot be applied.
In many instances the Laurent expansion of a function is not found through the
use of the formula (6.34), but rather by algebraic manipulations suggested by the
nature of the functio n. In particular, in dealing with quotients of polynomials it is
often advantageous to express them in terms of partial fractions and then expand
the various denominators in series of the appropriate form through the use of the
binomial expansion, which we assume the reader is familiar with:
s t
n
s
n
ns
nÿ1
t
nn ÿ 1
2!
s
nÿ2
t
2
nn ÿ 1n ÿ 2
3!
s
nÿ3
t
3
:
This expansion is valid for all values of n if jsj > jtj: If jsjjtj the expansion is
valid only if n is a non-negative integer.
That such procedures are correct follows from the fact that the Laurent expan-
sion of a function over a given annular ring is unique. That is, if an expansion of the
Laurent type is found by any process, it must be the Laurent expansion.
Example 6.23
Find the Laur ent expansion of the function f z7z ÿ 2=z 1zz ÿ 2 in
the annulus 1 < jz 1j < 3.
277
SERIES REPRESENTATIONS OF ANALYTIC FUNCTIONS
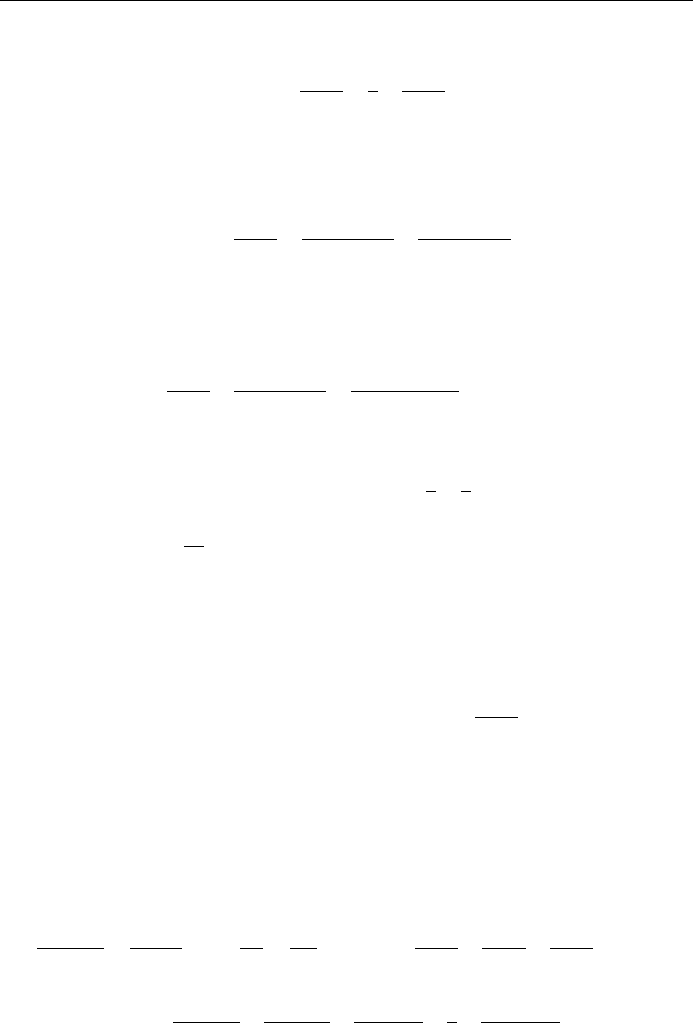
Solution: We ®rst apply the method of partial fractions to f z and obtain
f z
ÿ3
z 1
1
z
2
z ÿ 2
:
Now the center of the given annulus is z ÿ1, so the series we are seeking must
be one involv ing powers of z 1. This means that we have to modify the second
and third terms in the parti al fraction representation of f z:
f z
ÿ3
z 1
1
z 1ÿ1
2
z 1ÿ3
;
but the series for z 1ÿ3
ÿ1
converges only where jz 1j > 3, whereas we
require an expansion valid for jz 1j < 3. Hence we rewrite the third term in
the other order:
f z
ÿ3
z 1
1
z 1ÿ1
2
ÿ3 z 1
ÿ3z 1
ÿ1
z 1ÿ1
ÿ1
2ÿ3 z 1
ÿ1
z 1
ÿ2
ÿ 2z 1
ÿ1
ÿ
2
3
ÿ
2
9
z 1
ÿ
2
27
z 1
2
ÿ; 1 < jz 1j < 3:
Example 6.24
Given the following two functions:
a e
3z
z 1
ÿ3
; bz 2sin
1
z 2
;
®nd Laurent series about the singularity for each of the functions, name the
singularity, and give the region of convergence.
Solution: (a) z ÿ1 is a triple pole (pole of order 3). Let z 1 u, then
z u ÿ 1 and
e
3z
z 1
3
e
3uÿ1
u
3
e
ÿ3
e
3u
u
3
e
ÿ3
u
3
1 3u
3u
2
2!
3u
3
3!
3u
4
4!
þ!
e
ÿ3
1
z 1
3
3
z 1
2
9
2z 1
9
2
27z 1
8
þ!
:
The series converges for all values of z 6 ÿ1.
(b) z ÿ2 is an essential singularity. Let z 2 u, then z u ÿ 2, and
278
FUNCTIONS OF A COMPLEX VARIABLE

z 2sin
1
z 2
u sin
1
u
u
1
u
ÿ
1
3!u
3
1
5!u
5
1 ÿ
1
6z 2
2
1
120z 2
4
ÿ:
The series converges for all values of z 6 ÿ2.
Integration by the method of residues
We now turn to integration by the method of residues which is useful in evaluat-
ing both real and complex integrals. We ®rst discuss brie¯y the theory of residues,
then apply it to evaluate certain types of real de®nite integrals occurring in physics
and engineering.
Residues
If f z is single-valued and analytic in a neighborhood of a point z a, then, by
Cauchy's integral theorem,
I
C
f zdz 0
for any contour in that neighborhood. But if f z has a pole or an isolated
essential singularity at z a and lies in the interior of C, then the above integral
will, in general, be diÿerent from zero . In this case we may represent f z by a
Laurent series:
f z
X
1
nÿ1
a
n
z ÿ a
n
a
0
a
1
z ÿ aa
2
z ÿ a
2
a
ÿ1
z ÿ a
a
ÿ2
z ÿ a
2
;
where
a
n
1
2i
I
C
f z
z ÿ a
n1
dz; n 0; 1; 2; ...:
The sum of all the terms containing negative powers, namely
a
ÿ1
=z ÿ a a
ÿ2
=z ÿ a
2
; is called the principal part of f z at z a.In
the specia l case n ÿ1, we have
a
ÿ1
1
2i
I
C
f zdz
or
I
C
f zdz 2ia
ÿ1
; 6:36
279
INTEGRATION BY THE METHOD OF RESIDUES

the integration being taken in the counterclockwise sense around a simple closed
curve C that lies in the region 0 < jz ÿ aj < D and contains the point z a , where
D is the distance from a to the nearest singular point of f z. The coecient a
ÿ1
is
called the residue of f z at z a, and we shall use the notation
a
ÿ1
Res
za
f z: 6:37
We have seen that Laurent expansions can be obtained by various methods,
without using the integral formulas for the coecients. Hence, we may determine
the residue by one of those methods and then use the formula (6.36) to evaluate
contour integrals. To illustrate this, let us consider the following simple example.
Example 6.25
Integrate the function f zz
ÿ4
sin z around the unit circle C in the counter-
clockwise sense.
Solution: Using
sin z
X
1
n0
ÿ1
n
z
2n1
2n 1!
z ÿ
z
3
3!
z
5
5!
ÿ;
we obtain the Laurent series
f z
sin z
z
4
1
z
3
ÿ
1
3!z
z
5!
ÿ
z
3
7!
ÿ:
We see that f z has a pole of third order at z 0, the corresponding residue is
a
ÿ1
ÿ1=3!, and from Eq. (6.36) it follows that
I
sin z
z
4
dz 2ia
ÿ1
ÿi
3
:
There is a simple standard method for determining the residue in the case of a
pole. If f z has a simple pole at a point z a, the corresponding Laurent series is
of the form
f z
X
1
nÿ1
a
n
z ÿ a
n
a
0
a
1
z ÿ aa
2
z ÿ a
2
a
ÿ1
z ÿ a
;
where a
ÿ1
6 0. Multiplying both sides by z ÿ a,wehave
z ÿ af zz ÿ aa
0
a
1
z ÿ aa
ÿ1
and from this we have
Res
za
f za
ÿ1
lim
z!a
z ÿ af z: 6:38
280
FUNCTIONS OF A COMPLEX VARIABLE

Another useful formula is obtained as follows. If f z can be put in the form
f z
pz
qz
;
where pz and qz are analytic at z a; pz60, and qz0atz a (that is,
qz has a simple zero at z a. Consequently, qz can be expanded in a Taylor
series of the form
qzz ÿ aq
0
a
z ÿ a
2
2!
q
00
a:
Hence
Res
za
f zlim
z!a
z ÿ a
pz
qz
lim
z!a
z ÿ apz
z ÿ aq
0
az ÿ aq
00
a=2
pa
q
0
a
:
6:39
Example 6.26
The function f z4 ÿ 3z=z
2
ÿ z is analytic except at z 0 and z 1 where
it has simple poles. Find the residues at these poles.
Solution: We have pz4 ÿ 3z; qzz
2
ÿ z. Then from Eq. (6.39) we obtain
Res
z0
f z
4 ÿ 3z
2z ÿ 1
z0
ÿ4; Res
z1
f z
4 ÿ 3z
2z ÿ 1
z1
1:
We now consider poles of higher orders. If f z has a pole of order m > 1ata
point z a, the corresponding Laurent series is of the form
f za
0
a
1
z ÿ aa
2
z ÿ a
2
a
ÿ1
z ÿ a
a
ÿ2
z ÿ a
2
a
ÿm
z ÿ a
m
;
where a
ÿm
6 0 and the series converges in some neighb orhood of z a, except at
the point itself. By multiplying both sides by z ÿ a
m
we obtain
z ÿ a
m
f za
ÿm
a
ÿm1
z ÿ aa
ÿm2
z ÿ a
2
a
ÿmmÿ1
z ÿ a
mÿ1
z ÿ a
m
a
0
a
1
z ÿ a:
This represents the Taylor series about z a of the analytic function on the left
hand side. Diÿerentiating both sides (m ÿ 1) times with respect to z,wehave
d
mÿ1
dz
mÿ1
z ÿ a
m
f z m ÿ 1!a
ÿ1
mm ÿ 12a
0
z ÿ a:
281
INTEGRATION BY THE METHOD OF RESIDUES

Thus on letting z ! a
lim
z!a
d
mÿ1
dz
mÿ1
z ÿ a
m
f z m ÿ 1!a
ÿ1
;
that is,
Res
za
f z
1
m ÿ 1!
lim
z!a
d
mÿ1
dz
mÿ1
z ÿ a
m
f z
()
: 6:40
Of course, in the case of a rational function f z the residues can also be
determined from the representation of f z in terms of partial fractions.
The residue theorem
So far we have employed the residue method to evaluate contour integrals whose
integrands have only a single singularity inside the contour of integration. Now
consider a simple closed curve C containing in its interior a numb er of isolated
singularities of a function f z. If around each singular point we draw a circle so
small that it encloses no other singular poi nts (Fig. 6.15), these small circles,
together with the curve C, form the boundary of a multiply-connected region in
which f z is everywhere analytic and to which Cauchy's theorem can therefore be
applied. This gives
1
2i
I
C
f zdz
I
C
1
f zdz
I
C
m
f zdz
0:
If we reverse the direction of integration around each of the circles and change the
sign of each integral to compensate, this can be written
1
2i
I
C
f zdz
1
2i
I
C
1
f zdz
1
2i
I
C
2
f zdz
1
2i
I
C
m
f zdz;
282
FUNCTIONS OF A COMPLEX VARIABLE
Figure 6.15. Residue theorem.

where all the integrals are now to be taken in the cou nterclockwise sense. But the
integrals on the right are, by de®nition, just the residu es of f z at the various
isolated singularities within C. Hence we have established an important theorem,
the residu e theorem:
If f z is analytic inside a simple closed curve C and on C, except
at a ®nite number of singular points a
1
, a
2
; ...; a
m
in the interior of
C, then
I
C
f zdz 2i
X
m
j1
Res
za
j
f z2i r
1
r
2
r
m
; 6:41
where r
j
is the residue of f z at the singular point a
j
.
Example 6.27
The function f z4 ÿ 3z=z
2
ÿ z has simple poles at z 0 and z 1; the
residues are ÿ4 and 1, respectively (cf. Example 6.26). Therefore
I
C
4 ÿ 3z
z
2
ÿ z
dz 2iÿ4 1ÿ6i
for every simple closed curve C which encloses the points 0 and 1, and
I
C
4 ÿ 3z
z
2
ÿ z
dz 2iÿ4ÿ8i
for any simple closed curve C for which z 0 lies inside C and z 1 lies outside,
the integrations being taken in the counterclockwise sense.
Evaluation of real de®n ite integrals
The residue theorem yields a simple and elegant method for evaluating certain
classes of complicated real de®nite integrals. One serious restriction is that the
contour must be closed. But many integrals of practical interest involve integra-
tion over open curves. Their paths of integration must be closed before the residue
theorem can be applied. So our ability to evaluate such an integral depends
crucially on how the contour is closed, since it requires knowledge of the addi-
tional contributions from the added parts of the closed contour. A number of
techniques a re known for closing open contours. The following types are most
common in practice.
Improper integrals of the rational function
Z
1
ÿ1
f xdx
The improper integral has the meaning
Z
1
ÿ1
f xdx lim
a!1
Z
0
a
f xdx lim
b!1
Z
b
0
f xdx: 6:42
283
EVALUATION OF REAL DEFINITE INTEGRALS

If both limits exist, we may couple the two independent passages to ÿ1 and 1,
and write
Z
1
ÿ1
f xdx lim
r!1
Z
r
ÿr
f xdx: 6 :43
We assume that the function f x is a real rational function whose denominator
is diÿerent from zero for all real x and is of degree at least two units higher than
the degree of the numerator. Then the limits in (6.42) exist and we can start from
(6.43). We consider the corresponding contour integral
I
C
f zdz;
along a contour C consisting of the line along the x-axis from ÿr to r and the
semicircle ÿ above (or below) the x-axis having this line as its diameter (Fig. 6.16).
Then let r !1.Iff x is an even function this can be used to evaluat e
Z
1
0
f xdx:
Let us see why this works. Since f x is rational, f z has ®nitely many poles in the
upper half-plane, and if we choose r large enough, C encloses all these poles. Then
by the residue theorem we have
I
C
f zdz
Z
ÿ
f zdz
Z
r
ÿr
f xdx 2i
X
Res f z:
This gives
Z
r
ÿr
f xdx 2i
X
Res f zÿ
Z
ÿ
f zdz:
We next prove that
R
ÿ
f zdz ! 0ifr !1. To this end, we set z re
i
, then ÿ
is represented by r const, and as z ranges along ÿ; ranges from 0 to . Since
284
FUNCTIONS OF A COMPLEX VARIABLE
Figure 6.16. Path of the contour integral.

the degree of the denominator of f z is at least 2 units higher than the degree of
the numerator, we have
f z
jj
< k= z
jj
2
z
jj
r > r
0
for suciently large constants k and r. By applying (6.24) we thus obtain
Z
ÿ
f zdz
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
<
k
r
2
r
k
r
:
Hence, as r !1, the value of the integral over ÿ approaches zero, and we obtain
Z
1
ÿ1
f xdx 2i
X
Res f z: 6:44
Example 6.28
Using (6.44), show that
Z
1
0
dx
1 x
4
2
2
p
:
Solution: f z1=1 z
4
has four simple poles at the points
z
1
e
i=4
; z
2
e
3i=4
; z
3
e
ÿ3i=4
; z
4
e
ÿi=4
:
The ®rst two poles, z
1
and z
2
, lie in the upper half-plane (Fig. 6.17) and we ®nd,
using L'Hospital's rule
Res
zz
1
f z
1
1 z
4
0
zz
1
1
4z
3
zz
1
1
4
e
ÿ3i=4
ÿ
1
4
e
i=4
;
Res
zz
2
f z
1
1 z
4
0
zz
2
1
4z
3
zz
2
1
4
e
ÿ9i=4
1
4
e
ÿi=4
;
285
EVALUATION OF REAL DEFINITE INTEGRALS
Figure 6.17.
