Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.

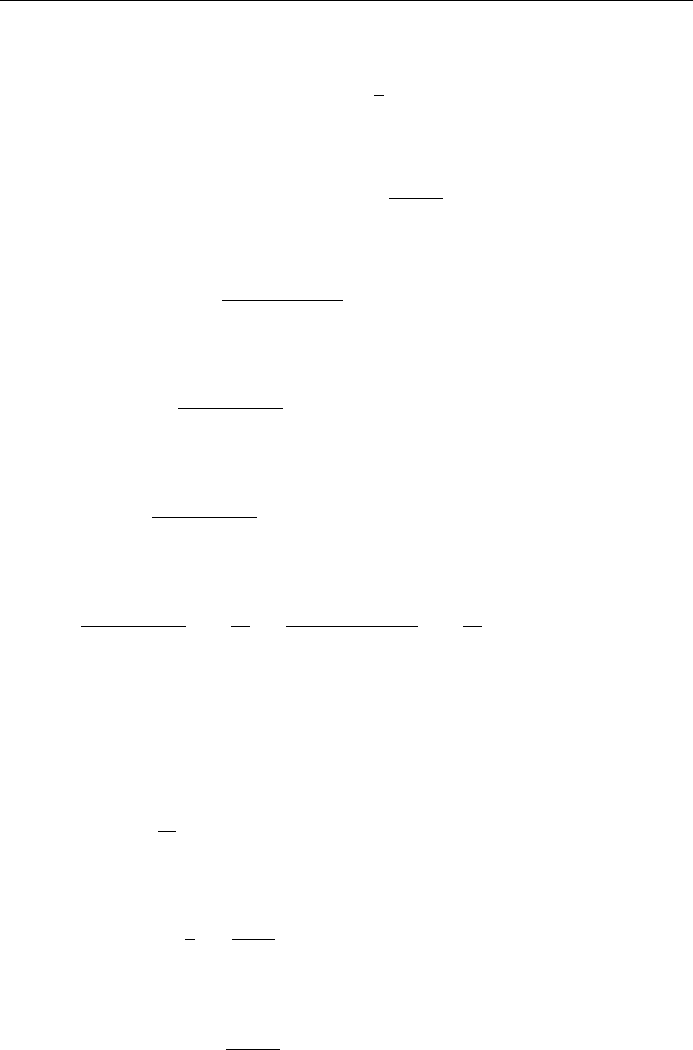
Substituting these into Eq. (7.24) we obtain
n
Z
1
ÿ1
P
n
x
2
dx 1 ÿ
1
2
Z
1
ÿ1
P
n
x
2
dx;
which can be simpli®ed to
Z
1
ÿ1
P
n
x
2
dx
2
2n 1
:
Alternatively, we can use generating function
1
1 ÿ 2xz z
2
p
X
1
n0
P
n
xz
n
:
We have on squaring both sides of this:
1
1 ÿ 2xz z
2
X
1
m0
X
1
n0
P
m
xP
n
xz
mn
:
Then by integrating from ÿ1 to 1 we have
Z
1
ÿ1
dx
1 ÿ 2xz z
2
X
1
m0
X
1
n0
Z
1
ÿ1
P
m
xP
n
xdx
z
mn
:
Now
Z
1
ÿ1
dx
1 ÿ 2xz z
2
ÿ
1
2z
Z
1
ÿ1
d1 ÿ 2xz z
2
1 ÿ 2xz z
2
ÿ
1
2z
ln1 ÿ 2xz z
2
j
1
ÿ1
and
Z
1
ÿ1
P
m
xP
n
xdx 0; m 6 n:
Thus, we have
ÿ
1
2z
ln1 ÿ 2xz z
2
j
1
ÿ1
X
1
n0
Z
1
ÿ1
P
2
n
xdx
z
2n
or
1
z
ln
1 z
1 ÿ z
X
1
n0
Z
1
ÿ1
P
2
n
xdx
z
2n
;
that is,
X
1
n0
2z
2n
2n 1
X
1
n0
Z
1
ÿ1
P
2
n
xdx
z
2n
:
Equating coecients of z
2n
we have as required
R
1
ÿ1
P
2
n
xdx 2=2n 1.
306
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS

Since the Legendre polynomials form a complete orthogonal set on (ÿ1, 1), we
can expand functions in Legendre series just as we expanded functions in Fourier
series:
f x
X
1
i0
c
i
P
i
x:
The coecients c
i
can be found by a method parallel to the one we used in ®nding
the formulas for the coecients in a Fourier series. We shall not pursue this line
further.
There is a second solution of Legendre's equation. However, this solution is
usually only required in practical applications in which jxj > 1 and we shall only
brie¯y discuss it for such values of x. Now solutions of Legendre's equation
relative to the regular singular point at in®nity can be investigated by writing
x
2
t. With this substitution,
dy
dx
dy
dt
dt
dx
2t
1=2
dy
dt
and
d
2
y
dx
2
d
dx
dy
dx
2
dy
dx
4t
d
2
y
dt
2
;
and Legendre's equation becomes, after some simpli®cations,
t1 ÿ t
d
2
y
dt
2
1
2
ÿ
3
2
t
dy
dt
1
4
y 0 :
This is the hypergeometric equati on with ÿ=2;þ 1 =2, and ÿ
1
2
:
x1 ÿ x
d
2
y
dx
2
ÿ ÿ þ 1 x
dy
dx
ÿ þy 0;
we shall not seek its solutions. The second solut ion of Legendre's equation is
commonly denoted by Q
x and is called the Legendre function of the second
kind of order . Thus the general solution of Legendre's equation (7.1) can be
written
y AP
xBQ
x;
A and B being arbitrary constants. P
x is called the Legendre function of the
®rst kind of order and it reduces to the Legendre polynomi al P
n
x when is an
integer n.
The associated Legendre functions
These are the functions of integral order which are solutions of the associated
Legendre equation
1 ÿ x
2
y
00
ÿ 2xy
0
nn 1ÿ
m
2
1 ÿ x
2
()
y 0 7:25
with m
2
n
2
.
307
THE ASSOCIATED LEGENDRE FUNCTIONS

We could solve Eq. (7.25) by series; but it is more useful to know how the
solutions are related to Legendre polynomials, so we shall proceed in the follow-
ing way. We write
y 1 ÿ x
2
m=2
ux
and substitute into Eq. (7.25) whence we get, after a little simpli®cation,
1 ÿ x
2
u
00
ÿ 2m 1xu
0
nn 1ÿmm 1u 0: 7:26
For m 0, this is a Legendre equation with solution P
n
x. Now we diÿerentiate
Eq. (7.26) and get
1 ÿ x
2
u
0
00
ÿ 2m 11xu
0
0
nn 1ÿm 1m 2u
0
0:
7:27
Note that Eq. (7.27) is just Eq. (7.26) with u
0
in place of u, and ( m 1) in place of
m. Thus, if P
n
x is a solution of Eq. (7.26) with m 0, P
0
n
x is a solution of Eq.
(7.26) with m 1, P
00
n
x is a solution with m 2, and in general for integral
m; 0 m n; d
m
=dx
m
P
n
x is a solution of Eq. (7.26). Then
y 1 ÿ x
2
m=2
d
m
dx
m
P
n
x7:28
is a solution of the associated Legendre equation (7.25). The functions in Eq.
(7.28) are called associ ated Legendre functions and are denoted by
P
m
n
x1 ÿ x
2
m=2
d
m
dx
m
P
n
x: 7 :29
Some authors include a factor (ÿ1
m
in the de®nition of P
m
n
x:
A negative value of m in Eq. (7.25) does not change m
2
, so a solution of Eq.
(7.25) for positive m is also a solution for the corresponding negative m . Thus
many references de®ne P
m
n
x for ÿn m n as eq ual to P
jmj
n
x.
When we write x cos , Eq. (7.25 ) becomes
1
sin
d
d
sin
dy
d
nn 1ÿ
m
2
sin
2
()
y 0 7:30
and Eq. (7.29) becomes
P
m
n
cos sin
m
d
m
dcos
m
P
n
cos
fg
:
In particular
D
ÿ1
means
Z
x
1
P
n
xdx:
308
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS
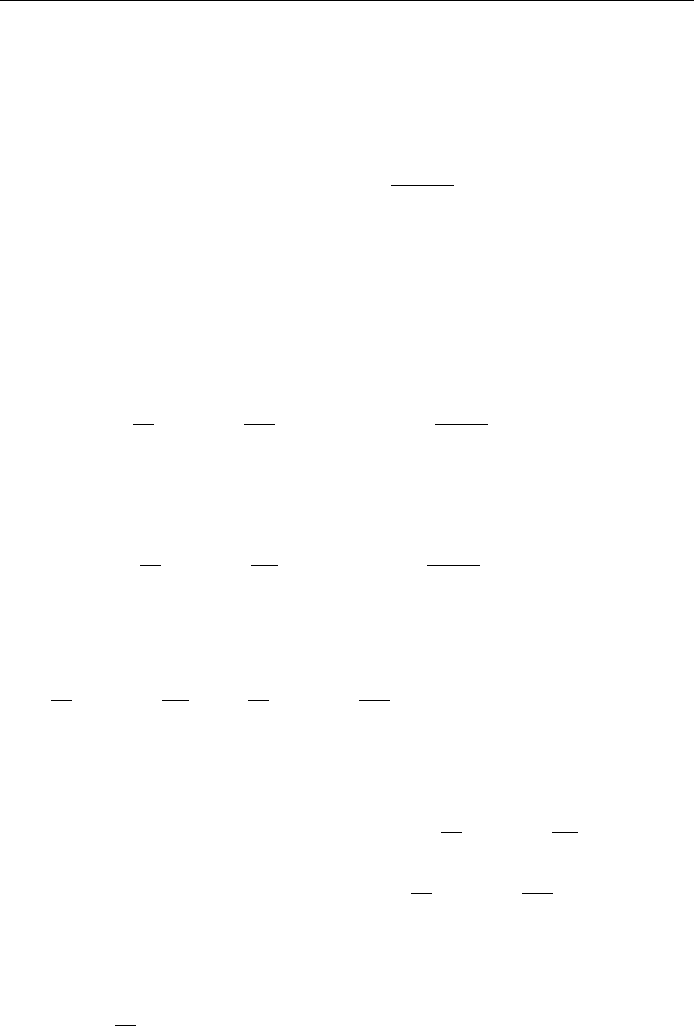
Orthogonality of associated Legendre functions
As in the case of Legendre polynomials, the associated Legendre functions P
m
n
x
are orthogonal for ÿ1 x 1 and in particular
Z
1
ÿ1
P
s
m
xP
s
n
xdx
n s !
n ÿ s !
mn
: 7:31
To prove this, let us write for simp licity
M P
m
s
x; and N P
s
n
x
and from Eq. (7.25), the associated Legendre equation, we have
d
dx
1 ÿ x
2
dM
dx
mm 1ÿ
s
2
1 ÿ x
2
()
M 0 7:32
and
d
dx
1 ÿ x
2
dN
dx
nn 1ÿ
s
2
1 ÿ x
2
()
N 0: 7:33
Multiplying Eq. (7.32) by N, Eq. (7.33) by M and subtracting, we get
M
d
dx
1 ÿ x
2
dN
dx
ÿ N
d
dx
1 ÿ x
2
dM
dx
fmm 1ÿnn 1gMN:
Integration between ÿ1 and 1 gives
m ÿ nm n ÿ 1
Z
1
ÿ1
MNdx
Z
1
ÿ1
M
d
dx
1 ÿ x
2
dN
dx
ÿ N
d
dx
1 ÿ x
2
dM
dx
dx: 7:34
Integration by parts gives
Z
1
ÿ1
M
d
dx
f1 ÿ x
2
N
0
gdx MN
0
1 ÿ x
2
1
ÿ1
ÿ
Z
1
ÿ1
1 ÿ x
2
M
0
N
0
dx
ÿ
Z
1
ÿ1
1 ÿ x
2
M
0
N
0
dx:
309
THE ASSOCIATED LEGENDRE FUNCTIONS

Then integrating by parts once more, we obtain
Z
1
ÿ1
M
d
dx
f1 ÿ x
2
N
0
gdx ÿ
Z
1
ÿ1
1 ÿ x
2
M
0
N
0
dx
ÿMN1 ÿ x
2
1
ÿ1
Z
1
ÿ1
N
d
dx
1 ÿ x
2
M
0
ÿ
dx
Z
1
ÿ1
N
d
dx
f1 ÿ x
2
M
0
gdx:
Substituting this in Eq. (7.34) we get
m ÿ nm n ÿ 1
Z
1
ÿ1
MNdx 0:
If m n, we have
Z
1
ÿ1
MNdx
Z
1
ÿ1
P
s
m
xP
s
m
xdx 0 m 6 n:
If m n, let us write
P
s
n
x1 ÿ x
2
s=2
d
s
dx
s
P
n
x
1 ÿ x
2
s=2
2
n
n!
d
sn
dx
sn
fx
2
ÿ 1
n
g:
Hence
Z
1
ÿ1
P
s
n
xP
s
n
xdx
1
2
2n
n!
2
Z
1
ÿ1
1 ÿ x
2
s
D
ns
fx
2
ÿ 1
n
gD
ns
fx
2
ÿ 1
n
gdx; D
k
d
k
=dx
k
:
Integration by parts gives
1
2
2n
n!
2
1 ÿ x
2
s
D
ns
fx
2
ÿ 1
n
gD
nsÿ1
fx
2
ÿ 1
n
g
1
ÿ1
ÿ
1
2
2n
n!
2
Z
1
ÿ1
D 1 ÿ x
2
s
D
ns
x
2
ÿ 1
n
ÿ
D
nsÿ1
x
2
ÿ 1
n
ÿ
dx:
The ®rst term vanishes at both limits and we have
Z
1
ÿ1
fP
s
n
xg
2
dx
ÿ1
2
2n
n!
2
Z
1
ÿ1
D1 ÿ x
2
s
D
ns
fx
2
ÿ 1
n
gD
nsÿ1
fx
2
ÿ 1
n
gdx:
7:35
We can continue to integrate Eq. (7.35) by parts and the ®rst term continues to
vanish since D
p
1 ÿ x
2
s
D
ns
fx
2
ÿ 1
n
g contains the factor 1 ÿ x
2
when p < s
310
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS

and D
nsÿp
fx
2
ÿ 1
n
g contains it when p s. After integrating n s times we
®nd
Z
1
ÿ1
fP
s
n
xg
2
dx
ÿ1
ns
2
2n
n!
2
Z
1
ÿ1
D
ns
1 ÿ x
2
s
D
ns
fx
2
ÿ 1
n
gx
2
ÿ 1
n
dx: 7:36
But D
ns
fx
2
ÿ 1
n
g is a polynomial of degree (n ÿ s) so that
(1 ÿ x
2
s
D
ns
fx
2
ÿ 1
n
g is of degree n ÿ 2 2s n s. Hence the ®rst factor
in the integrand is a polynomial of degree zero . We can ®nd this constant by
examining the following:
D
ns
x
2n
2n2n ÿ 12n ÿ 2n ÿ1x
nÿs
:
Hence the highest power in 1 ÿ x
2
s
D
ns
fx
2
ÿ 1
n
g is the term
ÿ1
s
2n2n ÿ 1n ÿ s 1 x
ns
;
so that
D
ns
1 ÿ x
2
s
D
ns
fx
2
ÿ 1
n
g ÿ1
s
2n!
n s!
n ÿ s!
:
Now Eq. (7.36) gives, by writing x cos ,
Z
1
ÿ1
P
s
n
fxg
2
dx
ÿ1
n
2
2n
n!
2
Z
1
ÿ1
2n!
n s!
n ÿ s!
x
2
ÿ 1
n
dx
2
2n 1
n s !
n ÿ s !
7:37
Hermite's equation
Hermite's equation is
y
00
ÿ 2xy
0
2y 0; 7:38
where y
0
dy=dx. The reader will see this equation in quantum mechanics (when
solving the Schro
È
dinger equation for a linear harmonic potential function).
The origin x 0 is an ordinary point and we may write the solution in the form
y a
0
a
1
x a
2
x
2
X
1
j0
a
j
x
j
: 7:39
Diÿerentiating the series term by term, we have
y
0
X
1
j0
ja
j
x
jÿ1
; y
00
X
1
j0
j 1j 2a
j2
x
j
:
311
HERMITE'S EQUATION

Substituting these into Eq. (7.38) we obtain
X
1
j0
j 1j 2a
j2
2 ÿ ja
j
x
j
0:
For a power series to vanish the coecient of each power of x must be zero; this
gives
j 1j 2a
j2
2 ÿ ja
j
0;
from which we obtain the recurrence relat ions
a
j2
2j ÿ
j 1j 2
a
j
: 7:40
We obtain polynomial solutions of Eq. (7.38) when n, a positive integer. Then
Eq. (7.40) gives
a
n2
a
n4
0:
For even n, Eq. (7.40) gives
a
2
ÿ1
2n
2!
a
0
; a
4
ÿ1
2
2
2
n ÿ 2 n
4!
a
0
; a
6
ÿ1
3
2
3
n ÿ 4n ÿ 2n
6!
a
0
and generally
a
n
ÿ1
n=2
2
n=2
nn ÿ 24 2
n!
a
0
:
This solution is called a Hermite polynomial of degree n and is written H
n
x.If
we choose
a
0
ÿ1
n=2
2
n=2
n!
nn ÿ 24 2
ÿ1
n=2
n!
n=2!
we can write
H
n
x2x
n
ÿ
nn ÿ 1
1!
2x
nÿ2
nn ÿ 1n ÿ 2n ÿ 3
2!
2x
nÿ4
: 7:41
When n is odd the polynomial solution of Eq. (7.38) can still be written as Eq.
(7.41) if we write
a
1
ÿ1
nÿ1=2
2n!
n=2 ÿ 1=2!
:
In particular ,
H
0
x1; H
1
x2x; H
3
x4x
2
ÿ 2; H
3
x8x
2
ÿ 12x;
H
4
x16x
4
ÿ 48x
2
12; H
5
x32x
5
ÿ 160x
3
120x; ... :
312
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS

Rodrigues' formula for Hermite polynomials H
n
x
The Hermite polynomials are also given by the form ula
H
n
xÿ1
n
e
x
2
d
n
dx
n
e
ÿx
2
: 7:42
To prove this formula, let us write q e
ÿx
2
. Then
Dq 2xq 0; D
d
dx
:
Diÿerentiate this (n 1) times by the Leibnitz' rule giving
D
n2
q 2xD
n1
q 2n 1D
n
q 0 :
Writing y ÿ1
n
D
n
q gives
D
2
y 2xDy 2n 1y 0 7:43
substitute u e
x
2
y then
Du e
x
2
f2xy Dyg
and
D
2
u e
x
2
fD
2
y 4xDy 4x
2
y 2yg:
Hence by Eq. (7.43) we get
D
2
u ÿ 2xDu 2nu 0;
which ind icates that
u ÿ1
n
e
x
2
D
n
e
ÿx
2
is a polynomial solution of Hermite's equation (7.38).
Recurrence relations for Hermite polynomials
Rodrigues' formula gives on diÿerentiation
H
0
n
xÿ1
n
2xe
x
2
D
n
e
ÿx
2
ÿ1
n
e
x
2
D
n1
e
ÿx
2
:
that is,
H
0
n
x2xH
n
xÿH
n1
x: 7:44
Eq. (7.44) gives on diÿerentiation
H
00
n
x2H
n
x2xH
0
n
xÿH
0
n1
x:
313
HERMITE'S EQUATION

Now H
n
x satis®es Hermite's equation
H
00
n
xÿ2xH
0
n
x2nH
n
x0:
Eliminating H
00
n
x from the last two equations, we obtain
2xH
0
n
xÿ2nH
n
x2H
n
x2xH
0
n
xÿH
0
n1
x
which redu ces to
H
0
n1
x2n 1H
n
x: 7:45
Replacing n by n 1 in Eq. (7.44), we have
H
0
n1
x2xH
n1
xÿH
n2
x:
Combining this with Eq. (7.45) we obtain
H
n2
x2xH
n1
xÿ2n 1H
n
x: 7:46
This will quickly give the higher polynomials.
Generating function for the H
n
x
By using Rodrigues' formula we can also ®nd a generating formula for the H
n
x.
This is
x; te
2txÿt
2
e
fx
2
ÿtÿx
2
g
X
1
n0
H
n
x
n!
t
n
: 7:47
Diÿerentiating Eq. (7.47) n times with respect to t we get
e
x
2
@
n
@t
n
e
ÿtÿx
2
e
x
2
ÿ1
n
@
n
@x
n
e
ÿtÿx
2
X
1
k0
H
nk
x
t
k
k!
:
Put t 0 in the last equation and we obtain Rodrigues' formula
H
n
xÿ1
n
e
x
2
d
n
dx
n
e
ÿx
2
:
The orthogonal Hermite functions
These are de®ned by
F
n
xe
ÿx
2
=2
H
n
x; 7:48
from which we have
DF
n
xÿxF
n
xe
ÿx
2
=2
H
0
n
x;
D
2
F
n
xe
ÿx
2
=2
H
00
n
xÿ2xe
ÿx
2
=2
H
0
n
xx
2
e
ÿx
2
=2
H
n
xÿF
n
x
e
ÿx
2
=2
H
00
n
xÿ2xH
0
n
x x
2
F
n
xÿF
n
x;
314
SPECIAL FUNCTIONS OF MATHEMATICAL PHYSICS

but H
00
n
xÿ2xH
0
n
xÿ2nH
n
x, so we can rewrite the last equation as
D
2
F
n
xe
ÿx
2
=2
ÿ2nH
0
n
x x
2
F
n
xÿF
n
x
ÿ2nF
n
xx
2
F
n
xÿF
n
x;
which gives
D
2
F
n
xÿx
2
F
n
x2n 1F
n
x0: 7:49
We can now show that the set fF
n
xg is orthogonal in the in®nite range
ÿ1 < x < 1. Multiplying Eq. (7.49) by F
m
x we have
F
m
xD
2
F
n
xÿx
2
F
n
xF
m
x2n 1F
n
xF
m
x0:
Interchanging m and n gives
F
n
xD
2
F
m
xÿx
2
F
m
xF
n
x2m 1F
m
xF
n
x0:
Subtracting the last two equations from the previous one and then integrating
from ÿ1 to 1,wehave
I
n;m
Z
1
ÿ1
F
n
xF
m
xdx
1
2n ÿ m
Z
1
ÿ1
F
00
n
F
m
ÿ F
00
m
F
n
dx:
The integration by parts gives
2n ÿ mI
n;m
F
0
n
F
m
ÿ F
0
m
F
n
1
ÿ1
ÿ
Z
1
ÿ1
F
0
n
F
0
m
ÿ F
0
m
F
0
n
dx:
Since the right hand side vanishes at both limits and if m 6 m, we have
I
n;m
Z
1
ÿ1
F
n
xF
m
xdx 0: 7:50
When n m we can proceed as follows
I
n;n
Z
1
ÿ1
e
ÿx
2
H
n
xH
n
xdx
Z
1
ÿ1
e
x
2
D
n
e
ÿx
2
D
m
e
ÿx
2
dx:
Integration by parts, that is,
R
udv uv ÿ
R
vdu with u e
ÿx
2
D
n
e
ÿx
2
and v D
nÿ1
e
ÿx
2
, gives
I
n;n
ÿ
Z
1
ÿ1
2xe
x
2
D
n
e
ÿx
2
e
x
2
D
n1
e
ÿx
2
D
nÿ1
e
ÿx
2
dx:
By using Eq. (7.43) which is true for y ÿ1
n
D
n
q ÿ1
n
D
n
e
ÿx
2
we obtain
I
n;n
Z
1
ÿ1
2ne
x
2
D
nÿ1
e
ÿx
2
D
nÿ1
e
ÿx
2
dx 2nI
nÿ1;nÿ1
:
315
HERMITE'S EQUATION
