Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.

then
Z
1
ÿ1
dx
1 x
4
2i
4
ÿe
i=4
e
ÿi=4
sin
4
2
p
and so
Z
1
0
dx
1 x
4
1
2
Z
1
ÿ1
dx
1 x
4
2
2
p
:
Example 6.29
Show that
Z
1
ÿ1
x
2
dx
x
2
1
2
x
2
2x 2
7
50
:
Solution: The poles of
f z
z
2
z
2
1
2
z
2
2z 2
enclosed by the contour of Fig. 6.17 are z i of order 2 and z ÿ1 i of order 1.
The residue at z i is
lim
z!i
d
dz
z ÿ i
2
z
2
z i
21
z ÿ i
2
z
2
2z 2
"#
9i ÿ 12
100
:
The residue at z ÿ1 i is
lim
z!ÿ1i
z 1 ÿ i
z
2
z
2
1
2
z 1 ÿ iz 1 i
3 ÿ 4i
25
:
Therefore
Z
1
ÿ1
x
2
dx
x
2
1
2
x
2
2x 2
2i
9i ÿ 12
100
3 ÿ 4i
25
7
50
:
Integrals of the rational functions of sin and cos
Z
2
0
Gsin ; cos d
Gsin ; cos is a real rational function of sin and cos ®nite on the interval
0 2. Let z e
i
, then
dz ie
i
d; or d dz=iz; sin z ÿ z
ÿ1
=2i; cos z z
ÿ1
=2
286
FUNCTIONS OF A COMPLEX VARIABLE
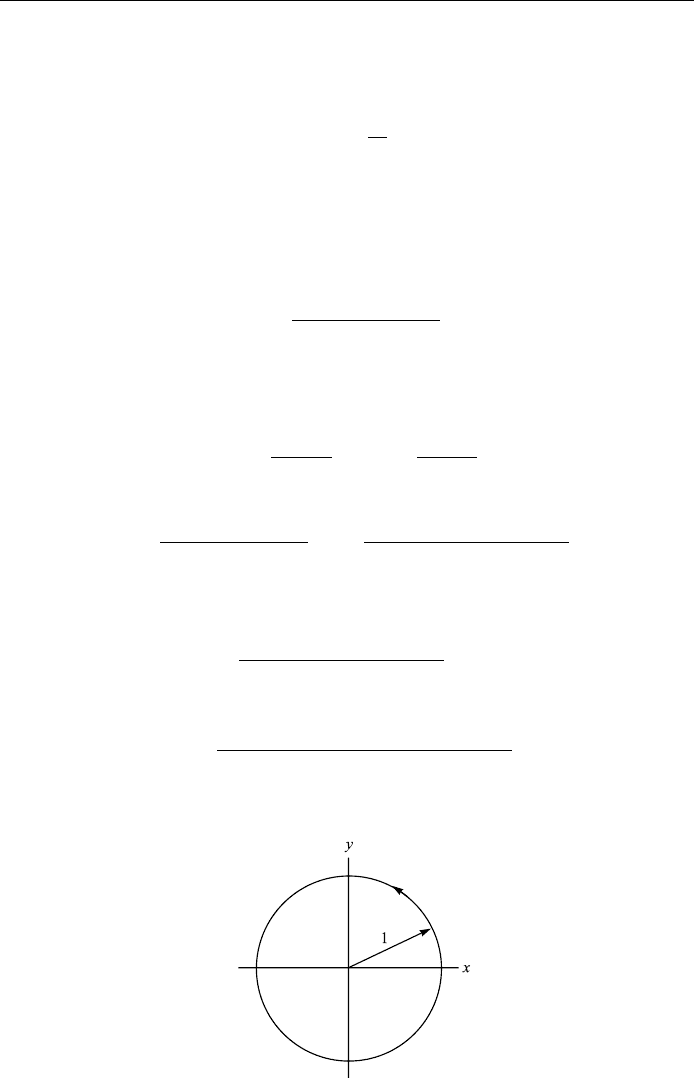
and the given integrand becomes a rational function of z, say, f z.As ranges
from 0 to 2, the variable z ranges once around the unit circle jzj1 in the
counterclockwise sense. The given integral takes the form
I
C
f z
dz
iz
;
the integration being taken in the counterclockwise sense around the unit circle.
Example 6.30
Evaluate
Z
2
0
d
3 ÿ 2cos sin
:
Solution: Let z e
i
, then dz ie
i
d,ord dz=iz, and
sin
z ÿ z
ÿ1
2i
; cos
z z
ÿ1
2
;
then
Z
2
0
d
3 ÿ 2 cos sin
I
C
2dz
1 ÿ 2i z
2
6iz ÿ 1 ÿ 2i
;
where C is the circle of unit radius with its center at the origin (Fig. 6.18).
We need to ®nd the poles of
1
1 ÿ 2i z
2
6iz ÿ 1 ÿ 2i
:
z
ÿ6i
6i
2
ÿ 4 1 ÿ 2 iÿ1 ÿ 2i
q
21 ÿ 2i
2 ÿ i; 2 ÿ i=5;
287
EVALUATION OF REAL DEFINITE INTEGRALS
Figure 6.18.
only (2 ÿ i=5 lies inside C, and residue at this pole is
lim
z!2ÿi=5
z ÿ2 ÿ i=5
2
1 ÿ 2i z
2
6iz ÿ 1 ÿ 2i
lim
z!2ÿi=5
2
21 ÿ 2iz 6i
1
2i
by L'Hospital's rule:
Then
Z
2
0
d
3 ÿ 2cos sin
I
C
2dz
1 ÿ 2i z
2
6iz ÿ 1 ÿ 2i
2i1=2i:
Fourier integrals of the form
Z
1
ÿ1
f x
sin mx
cos mx
dx
If f x is a rational function satisfying the assumptions stated in connection with
improper integrals of rational functions, then the above integrals may be evalu-
ated in a similar way. Here we consider the corresponding integral
I
C
f ze
imz
dz
over the contour C as that in improper integrals of rational functions (Fig. 6.16),
and obtain the formula
Z
1
ÿ1
f xe
imx
dx 2 i
X
Resf ze
imz
m > 0; 6:45
where the sum consists of the residues of f ze
imz
at its poles in the upper half-
plane. Equating the real and imaginary parts on each side of Eq. (6.45), we obt ain
Z
1
ÿ1
f xcos mxdx ÿ2
X
Im Resf ze
imz
; 6:46
Z
1
ÿ1
f xsin mxdx 2
X
Re Resf ze
imz
: 6:47
To establish Eq. (6.45) we should now prove that the value of the integral over
the semicircle ÿ in Fig. 6.16 approaches zero as r !1. This can be done as
follows. Since ÿ lies in the upper half-plane y 0andm > 0, it follows that
je
imz
jje
imx
j e
ÿmy
jj
e
ÿmy
1 y 0; m > 0 :
From this we obtain
jf ze
imz
j f z
jj
je
imz
j f z
jj
y 0; m > 0;
which reduces our present problem to that of an improper integral of a rational
function of this section, since f x is a rational function satisfying the assumptions
288
FUNCTIONS OF A COMPLEX VARIABLE
stated in connection these improper integrals. Continuing as before, we see that
the value of the integral under consideration approaches zero as r approaches 1,
and Eq. (6.45) is established.
Example 6.31
Show that
Z
1
ÿ1
cos mx
k
2
x
2
dx
k
e
ÿkm
;
Z
1
ÿ1
sin mx
k
2
x
2
dx 0 m > 0; k > 0:
Solution: The function f ze
imz
=k
2
z
2
has a simple pole at z ik which
lies in the upper half-plane. The residue of f z at z ik is
Res
zik
e
imz
k
2
z
2
e
imz
2z
zik
e
ÿmk
2ik
:
Therefore
Z
1
ÿ1
e
imx
k
2
x
2
dx 2i
e
ÿmk
2ik
k
e
ÿmk
and this yields the above results.
Other types of real improper integrals
These are de®nite integrals
Z
B
A
f xdx
whose integrand becomes in®nite at a point a in the interval of integration,
lim
x!a
f x
jj
1. This means that
Z
B
A
f xdx lim
"!0
Z
aÿ"
A
f xdx lim
!0
Z
a
f xdx;
where both " and approach zero independently and through positive values. It
may happen that neither of these limits exists when "; ! 0 independently, but
lim
"!0
Z
aÿ"
A
f xdx
Z
B
a"
f xdx
exists; this is called Cauchy's principal value of the integral and is often written
pr: v:
Z
B
A
f xdx:
289
EVALUATION OF REAL DEFINITE INTEGRALS
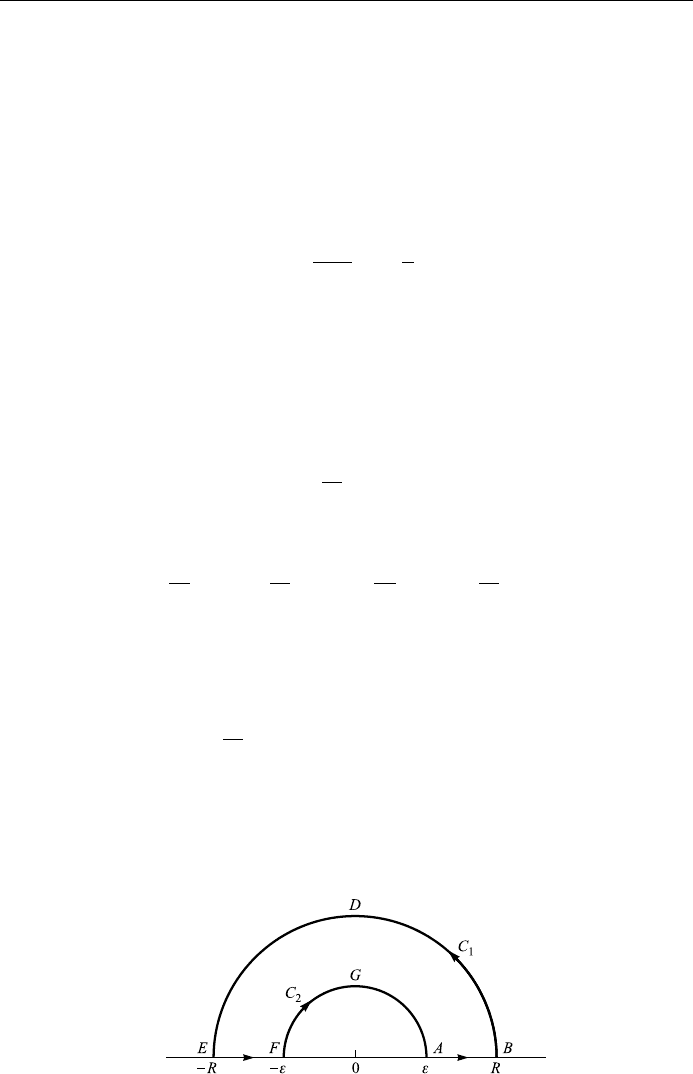
To evaluate improper integrals whose integrands have poles on the real axis, we
can use a path which avoids these singularities by following small semicircles with
centers at the singular points. We now illustrate the procedure with a simple
example.
Example 6.32
Show that
Z
1
0
sin x
x
dx
2
:
Solution: The function sin z=z does not behave suitably at in®nity. So we co n-
sider e
iz
=z, which has a simple pole at z 0, and integrate around the contour C
or ABDEFGA (Fig. 6.19). Since e
iz
=z is analytic inside and on C, it follows from
Cauchy's integral theorem that
I
C
e
iz
z
dz 0
or
Z
ÿ"
ÿR
e
ix
x
dx
Z
C
2
e
iz
z
dz
Z
R
"
e
ix
x
dx
Z
C
1
e
iz
z
dz 0: 6:48
We now prove that the value of the integral over large semicircle C
1
approaches
zero as R approaches in®nity. Setting z Re
i
, we have dz iRe
i
d; dz=z id
and therefore
Z
C
1
e
iz
z
dz
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
Z
0
e
iz
id
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
Z
0
e
iz
ÿ
ÿ
ÿ
ÿ
d:
In the integrand on the right,
e
iz
ÿ
ÿ
ÿ
ÿ
je
iRcos i sin
jje
iR cos
jje
ÿR sin
je
ÿR sin
:
290
FUNCTIONS OF A COMPLEX VARIABLE
Figure 6.19.

By inserting this and using sin( ÿ sin we obtain
Z
0
e
iz
ÿ
ÿ
ÿ
ÿ
d
Z
0
e
ÿR sin
d 2
Z
=2
0
e
ÿR sin
d
2
Z
"
0
e
ÿR sin
d
Z
=2
"
e
ÿR sin
d
"#
;
where " has any value between 0 and =2. The absolut e values of the integrands in
the ®rst and the last integrals on the right are at most equal to 1 and e
ÿR sin "
,
respectively, because the integrands are monotone decreasing functions of in the
interval of integration. Consequently, the whole expression on the right is smaller
than
2
Z
"
0
d e
ÿR sin
Z
=2
"
d
2 " e
ÿR sin
2
ÿ "
< 2" e
ÿR sin "
:
Altogether
Z
C
1
e
iz
z
dz
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
ÿ
< 2" e
ÿR sin "
:
We ®rst take " arbitrarily small. Then, having ®xed ", the last term can be made as
small as we please by choosing R suciently large. Hence the value of the integral
along C
1
approaches 0 as R !1.
We next prove that the value of the integral over the small semicircle C
2
approaches zero as " ! 0. Let z "
i
, then
Z
C
2
e
iz
z
dz ÿlim
"!0
Z
0
expi"e
i
"e
i
i"e
i
d ÿlim
"!0
Z
0
i expi"e
i
d i
and Eq. (6.48) reduces to
Z
ÿ"
ÿR
e
ix
x
dx i
Z
R
"
e
ix
x
dx 0:
Replacing x by ÿx in the ®rst integral and combining with the last integral, we
®nd
Z
R
"
e
ix
ÿ e
ÿix
x
dx i 0:
Thus we have
2i
Z
R
"
sin x
x
dx i:
291
EVALUATION OF REAL DEFINITE INTEGRALS

Taking the limits R !1and " ! 0
Z
1
0
sin x
x
dx
2
:
Problems
6.1. Given three complex numbers z
1
a ib, z
2
c id, and z
3
g ih,
show that:
(a) z
1
z
2
z
2
z
1
commutative law of addition;
(b) z
1
z
2
z
3
z
1
z
2
z
3
associative law of addition;
(c) z
1
z
2
z
2
z
1
commutative law of multiplication;
(d) z
1
z
2
z
3
z
1
z
2
z
3
associative law of multiplication.
6.2. Given
z
1
3 4i
3 ÿ 4i
; z
2
1 2i
1 ÿ 3i
2
®nd their polar forms, complex conjugates, moduli, product, the quotient
z
1
=z
2
:
6.3. The absolute value or modulus of a complex number z x iy is de®ned as
z
jj
zz*
p
x
2
y
2
q
:
If z
1
; z
2
; ...; z
m
are complex numbers, show that the following hold:
(a) jz
1
z
2
jjz
1
jjz
2
j or jz
1
z
2
z
m
jjz
1
jjz
2
jjz
m
j:
(b) jz
1
=z
2
jjz
1
j=jz
2
j if z
2
6 0:
(c) jz
1
z
2
jjz
1
jjz
2
j:
(d) jz
1
z
2
jjz
1
jÿjz
2
j or jz
1
ÿ z
2
jjz
1
jÿjz
2
j.
6.4 Find all roots of (a)
ÿ32
5
p
, and (b)
1 i
3
p
, and locate them in the complex
plane.
6.5 Show, using De Moivre's theorem, that:
(a) cos 5 16 cos
5
ÿ 20 cos
3
5cos;
(b) sin 5 5 cos
4
sin ÿ 10 cos
2
sin
3
sin
5
.
6.6 Given z re
i
, interpret ze
i
, where is real geometrically.
6.7 Solve the quadratic equation az
2
bz c 0; a 6 0.
6.8 A point P moves in a counterclockwise direction around a circle of radius 1
with center at the origin in the z plane. If the mapping function is w z
2
,
show that when P makes one complete revolution the image P
0
of P in the w
plane makes three complete revolutions in a counterclockwise direction on a
circle of radius 1 with center at the origin.
6.9 Show that f zln z has a branch point at z 0.
6.10 Let w f z z
2
1
1=2
, show that:
292
FUNCTIONS OF A COMPLEX VARIABLE

(a) f z has branch points at z I.
(b) a complete circuit around both branch points produces no change in the
branches of f z.
6.11 Apply the de®nition of limits to prove that:
lim
z!1
z
2
ÿ 1
z ÿ 1
2:
6.12. Prove that:
(a) f zz
2
is continuou s at z z
0
,and
(b) f z
z
2
; z 6 z
0
0; z z
0
(
is discontinuous at z z
0
, where z
0
6 0.
6.13 Given f zz*, show that f
0
i does not exist.
6.14 Using the de®nition, ®nd the derivative of f zz
3
ÿ 2z at the point where:
(a) z z
0
, and (b) z ÿ1.
6.15. Show that f is an analytic function of z if it does not depend on
z*: f z; z*f z . In other words, f x; yf x iy, that is, x and y
enter f only in the combination x+iy.
6.16. (a) Show that u y
3
ÿ 3x
2
y is harmonic.
(b) Find v such that f zu iv is analytic.
6.17 (a)Iff zux; yiv x; y is analytic in some region R of the z plane,
show that the one-para meter families of curves ux; yC
1
and
vx; yC
2
are orthogonal families.
(b) Illustrate (a) by using f zz
2
.
6.18 For each of the following functions locate and name the singularities in the
®nite z plane:
(a) f z
z
z
2
4
4
; (b) f z
sin
z
p
z
p
; (c) f z
P
1
n0
1
z
n
n!
:
6.19 (a) Locate and name all the singularities of
f z
z
8
z
4
2
z ÿ 1
3
3z 2
2
:
(b) Determine where f z is analytic.
6.20 (a) Given e
z
e
x
cos y i sin y, show that d=dze
z
e
z
.
(b) Show that e
z
1
e
z
2
e
z
1
z
2
.
(Hint: set z
1
x
1
iy
1
and z
2
x
2
iy
2
and apply the addition formulas
for the sine and cosine.)
6.21 Show that: (a)lne
z
z 2ni,(b)lnz
1
=z
2
ln z
1
ÿ ln z
2
2ni.
6.22 Find the values of: (a) ln i,(b)ln(1ÿ i).
6.23 Evaluate
R
C
z*dz from z 0toz 4 2i along the curve C given by:
(a) z t
2
it;
(b) the line from z 0toz 2i and then the line from z 2i to z 4 2i .
293
PROBLEMS

6.24 Evaluate
H
C
dz=z ÿ a
n
; n 2; 3; 4; ... where z a is inside the simp le
closed curve C.
6.25 If f z is analytic in a simply-connected region R, and a and z are any two
points in R, show that the integral
Z
z
a
f zdz
is independent of the path in R joining a and z.
6.26 Let f z be continuous in a simply-connected region R and let a and z be
points in R. Prove that Fz
R
z
a
f z
0
dz
0
is analytic in R, and F
0
zf z.
6.27 Evaluate
(a)
I
C
sin z
2
cos z
2
z ÿ 1z ÿ 2
dz
(b)
I
C
e
2z
z 1
4
dz,
where C is the circle jzj1.
6.28 Evaluate
I
C
2 sin z
2
z ÿ 1
4
dz;
where C is any simple closed path not passing through 1.
6.29 Show that the complex sequence
z
n
1
n
ÿ
n
2
ÿ 1
n
i
diverges.
6.30 Find the region of convergence of the series
P
1
n1
z 2
n1
=n 1
3
4
n
.
6.31 Find the Maclaurin series of f z1=1 z
2
.
6.32 Find the Taylor series of f zsin z about z =4, and determine its circle
of convergence. (Hint: sin z sina z ÿ a:
6.33 Find the Laurent series about the indicated singularity for each of the
following functions. Name the singularity in each case and give the region
of convergence of each series.
(a) z ÿ 3sin
1
z 2
; z ÿ2;
(b)
z
z 1z 2
; z ÿ2;
(c)
1
zz ÿ 3
2
; z 3:
6.34 Expand f z1=z 1z 3 in a Laurent series valid for:
(a)1< jzj < 3, (b) jzj > 3, (c)0< jz 1j < 2.
294
FUNCTIONS OF A COMPLEX VARIABLE

6.35 Evaluate
Z
1
ÿ1
x
2
dx
x
2
a
2
x
2
b
2
; a > 0; b > 0:
6.36 Evaluate
a
Z
2
0
d
1 ÿ 2p cos p
2
;
where p is a ®xed number in the interval 0 < p < 1;
b
Z
2
0
d
5 ÿ 3 sin
2
:
6.37 Evaluate
Z
1
ÿ1
x sin x
x
2
2x 5
dx:
6.38 Show that:
a
Z
1
0
sin x
2
dx
Z
1
0
cos x
2
dx
1
2
2
r
;
b
Z
1
0
x
pÿ1
1 x
dx
sin p
; 0 < p < 1:
295
PROBLEMS
