Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


180 Г л а в а 7. Последовательности
При вычислении пределов выражений, содержащих поаза-
тельные фунции с натуральным арументом, используют сле-
дующее равенство:
q
n
= 0, если | q | < 1. (4)
П р и м е р 2. Вычислить предел
Р е ш е н и е. Разделим числитель и знаменатель дроби на
Далее, применяя формулу (4), получаем
= = = 3.
Ответ.3.
Вычислите предел:
5.
6.
При вычислении пределов инода удобно пользоваться сле-
дующим свойством последовательностей
: если члены двух по-
следовательностей (a
n
) и (b
n
) связаны соотношением
|a
n
| m |b
n
|,
то из равенства нулю предела последовательности (b
n
) сле-
дует равенство нулю предела последовательности (a
n
).
П р и м е р 3. Вычислить предел .
Р е ш е н и е. Убедимся сначала в том, что при всех n Ý N
справедливо неравенство
< .
Действительно, разделив на n числитель и знаменатель дроби,
записанной в левой части неравенства, получим очевидное не-
равенство
< .
n º×
lim
n º×
lim
2
n 1+
3
n 1+
+
2
n
3
n
+
----------------------------------- - .
3
n 1+
.
n º×
lim
2
3
---
n 1+
1+
1
3
---
2
3
---
n
1
3
---
+
-------------------------------- -
2
3
---
n 1+
n º×
lim 1+
1
3
---
2
3
---
n
n º×
lim
1
3
---
+
---------------------------------------------- -
01+
1
3
---
0⋅
1
3
---
+
----------------------
n º×
lim
2
n
3
n
+
2
n
3
n
–
------------------- - .
n º×
lim
3 · 2
n 1+
7· 3
n
–1+
2
n 1+
5 · 3
n 1+
–6+
------------------------------------------------------ - .
n º×
lim
n
2n 1+
------------------
n
n
2n 1+
------------------
1
2
---
1
2
1
n
---
+
--------------
1
2
---
§ 37. Вычисление пределов последовательностей 181
Далее, используя свойство степеней, залючаем, что при всех
n Ý N справедливо неравенство
< .
Соласно формуле (4), имеем = 0, поэтому из приве-
денноо выше свойства последовательности вытеает, что
= 0.
Ответ.0.
Вычислите предел:
7. . 8. .
9.
При вычислении пределов, содержащих иррациональности,
часто используют перевод иррациональности из знаменателя
в числитель или наоборот.
П р и м е р 4. Вычислить предел ( – n).
Р е ш е н и е. Умножим и разделим выражение, находящее-
ся под знаом предела, на сопряженное выражение. Тода по-
лучим
=
= = .
Разделив числитель и знаменатель на n, находим
= = 1.
Ответ.1.
1
2
1
n
---
+
--------------
n
1
2
---
n
n º×
lim
1
2
---
n
n º×
lim
n
2n 1+
------------------
n
n º×
lim
3n 1+
4n 5+
------------------
n
n º×
lim
n
2
1–
2n 1+()n 2+()
------------------------------------------
n
n º×
lim
nsin n!
n
2
1+
------------------- .
n º×
lim n
2
2n+
n º×
lim
n
2
2n+ n–()n
2
2n+ n+()
n
2
2n+ n+
-----------------------------------------------------------------------------------
n º×
lim
n
2
2nn
2
–+
n
2
2n+ n+
------------------------------------
n º×
lim
2n
n
2
2n+ n+
------------------------------------
n º×
lim
2n
n
2
2n+ n+
------------------------------------
n º×
lim
2
1
2
n
---
+1+
-----------------------------

180 Г л а в а 7. Последовательности
При вычислении пределов выражений, содержащих поаза-
тельные фунции с натуральным арументом, используют сле-
дующее равенство:
q
n
= 0, если | q | < 1. (4)
П р и м е р 2. Вычислить предел
Р е ш е н и е. Разделим числитель и знаменатель дроби на
Далее, применяя формулу (4), получаем
= = = 3.
Ответ.3.
Вычислите предел:
5.
6.
При вычислении пределов инода удобно пользоваться сле-
дующим свойством последовательностей
: если члены двух по-
следовательностей (a
n
) и (b
n
) связаны соотношением
|a
n
| m |b
n
|,
то из равенства нулю предела последовательности (b
n
) сле-
дует равенство нулю предела последовательности (a
n
).
П р и м е р 3. Вычислить предел .
Р е ш е н и е. Убедимся сначала в том, что при всех n Ý N
справедливо неравенство
< .
Действительно, разделив на n числитель и знаменатель дроби,
записанной в левой части неравенства, получим очевидное не-
равенство
< .
n º×
lim
n º×
lim
2
n 1+
3
n 1+
+
2
n
3
n
+
----------------------------------- - .
3
n 1+
.
n º×
lim
2
3
---
n 1+
1+
1
3
---
2
3
---
n
1
3
---
+
-------------------------------- -
2
3
---
n 1+
n º×
lim 1+
1
3
---
2
3
---
n
n º×
lim
1
3
---
+
---------------------------------------------- -
01+
1
3
---
0⋅
1
3
---
+
----------------------
n º×
lim
2
n
3
n
+
2
n
3
n
–
------------------- - .
n º×
lim
3 · 2
n 1+
7· 3
n
–1+
2
n 1+
5 · 3
n 1+
–6+
------------------------------------------------------ - .
n º×
lim
n
2n 1+
------------------
n
n
2n 1+
------------------
1
2
---
1
2
1
n
---
+
--------------
1
2
---
§ 37. Вычисление пределов последовательностей 181
Далее, используя свойство степеней, залючаем, что при всех
n Ý N справедливо неравенство
< .
Соласно формуле (4), имеем = 0, поэтому из приве-
денноо выше свойства последовательности вытеает, что
= 0.
Ответ.0.
Вычислите предел:
7. . 8. .
9.
При вычислении пределов, содержащих иррациональности,
часто используют перевод иррациональности из знаменателя
в числитель или наоборот.
П р и м е р 4. Вычислить предел ( – n).
Р е ш е н и е. Умножим и разделим выражение, находящее-
ся под знаом предела, на сопряженное выражение. Тода по-
лучим
=
= = .
Разделив числитель и знаменатель на n, находим
= = 1.
Ответ.1.
1
2
1
n
---
+
--------------
n
1
2
---
n
n º×
lim
1
2
---
n
n º×
lim
n
2n 1+
------------------
n
n º×
lim
3n 1+
4n 5+
------------------
n
n º×
lim
n
2
1–
2n 1+()n 2+()
------------------------------------------
n
n º×
lim
nsin n!
n
2
1+
------------------- .
n º×
lim n
2
2n+
n º×
lim
n
2
2n+ n–()n
2
2n+ n+()
n
2
2n+ n+
-----------------------------------------------------------------------------------
n º×
lim
n
2
2nn
2
–+
n
2
2n+ n+
------------------------------------
n º×
lim
2n
n
2
2n+ n+
------------------------------------
n º×
lim
2n
n
2
2n+ n+
------------------------------------
n º×
lim
2
1
2
n
---
+1+
-----------------------------
182 Г л а в а 7. Последовательности
Вычислите предел:
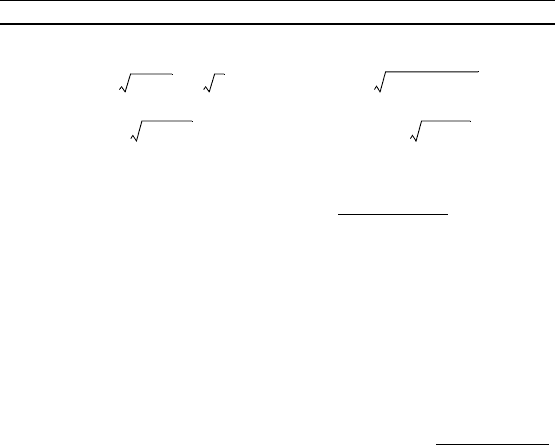
10. ( – ).11. ( – n).
12. n( – n).
13. (n + ).
Чтобы установить сходимость монотонной последователь-
ности, можно использовать следующее утверждение
: еcли после-
довательность монотонно возрастает (убывает), то для ее
сходимости достаточно, чтобы она была ораничена свер-
ху (снизу).
В том случае, ода известно, что предел последовательнос-
ти существует, для ео вычисления в ряде случаев удобно ис-
пользовать формулу
x
n
= x
n + 1
.(5)
Убедиться в существовании предела последовательности, а
инода и найти ео можно, используя следующее утверждение:
если для трех последовательностей, начиная с неотороо N
справедливо неравенство
a
n
m b
n
m c
n
и a
n
= c
n
, то b
n
существует, причем
b
n
= a
n
. (6)
П р и м е р 5. Найти предел последовательности x
n
= q
n
, если
|q| < 1.
Р е ш е н и е. Представим последовательность в реуррент-
ном виде:
x
n + 1
= qx
n
.
Та а |q| < 1, то |x
n + 1
| < |x
n
| при любом n Ý N, т. е. последо-
вательность (|x
n
|) монотонно убывает. Далее, посольу |x
n
| l 0
при любом n Ý N, последовательность (|x
n
|) ораничена снизу.
Значит, последовательность (|x
n
|) сходится. Пусть |x
n
| = y.
Тода для вычисления y соласно формуле (5) получаем урав-
нение
y = |q|y.(*)
Но |q| < 1, поэтому уравнение (*) имеет единственный орень
y = 0.
n º×
lim n 2+ n
n º×
lim n
2
5n–6+
n º×
lim n
2
1+
n º×
lim 1 n
3
–
3
n º×
lim
n º×
lim
n º×
lim
n º×
lim
n º×
lim
n º×
lim
n º×
lim
n º×
lim
§ 37. Вычисление пределов последовательностей 183
Аналоично доазывается, что (–|x
n
|) = 0. Учитывая,
что неравенство –|x
n
| m x
n
m |x
n
| справедливо при всех n Ý N,
получаем x
n
= 0.
14. Последовательность (x
n
), первый член оторой x
1
= ,
определяется реуррентным соотношением
x
n + 1
= .
Найдите предел (x
n
).
15. Последовательность (x
n
), первый член оторой x
1
= 1, оп-
ределяется реуррентным соотношением
x
n + 1
= + (1 – 2a)x
n
+ a
2
.
Найдите предел (x
n
).
16. Последовательность задана реуррентным соотношением
x
n + 1
= + x
n
,
де x
1
> 0, a > 0. Найдите предел (x
n
).
17. Доажите, что последовательность, первый член ото-
рой x
1
= , а аждый следующий удовлетворяет реуррентно-
му соотношению
x
n
= + ,
возрастает и ораничена сверху. Найдите ее предел.
18. Найдите предел последовательности, у оторой
x
1
= , x
n
= – .
19. Последовательность определяется реуррентным соот-
ношением
x
n – 1
= 2x
n
+ ,
де a > 0 и x > 0. Доажите, что x
n
= .
n º×
lim
n º×
lim
2
2 x
n
+
x
n
2
1
2
---
a
x
n
------
a
2
---
a
2
---
x
n
2
1–
2
----------------
a
2
---
a
2
---
x
n
2
1–
2
----------------
1
3
---
a
x
n
2
------
n º×
lim a
3

182 Г л а в а 7. Последовательности
Вычислите предел:
10. ( – ).11. ( – n).
12. n( – n).
13. (n + ).
Чтобы установить сходимость монотонной последователь-
ности, можно использовать следующее утверждение
: еcли после-
довательность монотонно возрастает (убывает), то для ее
сходимости достаточно, чтобы она была ораничена свер-
ху (снизу).
В том случае, ода известно, что предел последовательнос-
ти существует, для ео вычисления в ряде случаев удобно ис-
пользовать формулу
x
n
= x
n + 1
.(5)
Убедиться в существовании предела последовательности, а
инода и найти ео можно, используя следующее утверждение:
если для трех последовательностей, начиная с неотороо N
справедливо неравенство
a
n
m b
n
m c
n
и a
n
= c
n
, то b
n
существует, причем
b
n
= a
n
. (6)
П р и м е р 5. Найти предел последовательности x
n
= q
n
, если
|q| < 1.
Р е ш е н и е. Представим последовательность в реуррент-
ном виде:
x
n + 1
= qx
n
.
Та а |q| < 1, то |x
n + 1
| < |x
n
| при любом n Ý N, т. е. последо-
вательность (|x
n
|) монотонно убывает. Далее, посольу |x
n
| l 0
при любом n Ý N, последовательность (|x
n
|) ораничена снизу.
Значит, последовательность (|x
n
|) сходится. Пусть |x
n
| = y.
Тода для вычисления y соласно формуле (5) получаем урав-
нение
y = |q|y.(*)
Но |q| < 1, поэтому уравнение (*) имеет единственный орень
y = 0.
n º×
lim n 2+ n
n º×
lim n
2
5n–6+
n º×
lim n
2
1+
n º×
lim 1 n
3
–
3
n º×
lim
n º×
lim
n º×
lim
n º×
lim
n º×
lim
n º×
lim
n º×
lim
n º×
lim
§ 37. Вычисление пределов последовательностей 183
Аналоично доазывается, что (–|x
n
|) = 0. Учитывая,
что неравенство –|x
n
| m x
n
m |x
n
| справедливо при всех n Ý N,
получаем x
n
= 0.
14. Последовательность (x
n
), первый член оторой x
1
= ,
определяется реуррентным соотношением
x
n + 1
= .
Найдите предел (x
n
).
15. Последовательность (x
n
), первый член оторой x
1
= 1, оп-
ределяется реуррентным соотношением
x
n + 1
= + (1 – 2a)x
n
+ a
2
.
Найдите предел (x
n
).
16. Последовательность задана реуррентным соотношением
x
n + 1
= + x
n
,
де x
1
> 0, a > 0. Найдите предел (x
n
).
17. Доажите, что последовательность, первый член ото-
рой x
1
= , а аждый следующий удовлетворяет реуррентно-
му соотношению
x
n
= + ,
возрастает и ораничена сверху. Найдите ее предел.
18. Найдите предел последовательности, у оторой
x
1
= , x
n
= – .
19. Последовательность определяется реуррентным соот-
ношением
x
n – 1
= 2x
n
+ ,
де a > 0 и x > 0. Доажите, что x
n
= .
n º×
lim
n º×
lim
2
2 x
n
+
x
n
2
1
2
---
a
x
n
------
a
2
---
a
2
---
x
n
2
1–
2
----------------
a
2
---
a
2
---
x
n
2
1–
2
----------------
1
3
---
a
x
n
2
------
n º×
lim a
3

184 Г л а в а 7. Последовательности
20. Последовательность определяется реуррентным соот-
ношением
x
n + 1
= ,
де a > 0 и x > 0. Доажите, что x
n
= .
§ 38. Арифметическая прогрессия
Последовательность, у оторой задан первый член a
1
, а аж-
дый следующий член, начиная со второо, равен предыдуще-
му, сложенному с одним и тем же числом d, называют арифме-
тичесой прорессией. Таим образом,
a
n + 1
= a
n
+ d, n Ý N,(1)
де a
n
— n-й член прорессии, d— разность прорессии. Фор-
мула общео члена арифметичесой прорессии имеет вид
a
n
= a
1
+ d(n – 1). (2)
Сумма n членов арифметичесой прорессии вычисляется по
формулам
S
n
= n, (3)
S
n
= n.(4)
Свойство членов арифметичесой прорессии
. Любой член
арифметичесой прорессии (роме первоо) равен полусумме
равноотстоящих от нео членов:
a
n
= , k < n.(5)
Если k = 1, то формула (4) примет вид
a
n
= . (6)
Арифметичесая прорессия полностью определена, если
известны ее первый член a
1
и разность d.
x
n
x
n
2
2a+()
2x
n
3
a+
-------------------------------- -
n º×
lim a
3
a
1
a
n
+
2
-------------------
2a
1
dn 1–()+
2
--------------------------------------- -
a
nk–
a
nk+
+
2
-----------------------------------
a
n 1–
a
n 1+
+
2
-----------------------------------
§ 38. Арифметическая прогрессия 185
П р и м е р 1. При делении 9-о члена арифметичесой про-
рессии на ее второй член в частном получается 5, а при де-
лении 13-о члена этой прорессии на ее 6-й член в частном по-
лучается 2 и в остате 5. Найти первый член и разность про-
рессии.
Р е ш е н и е. Условие задачи можно записать в виде сле-
дующей системы уравнений:
Используя формулу общео члена арифметичесой прорессии,
приходим системе
оторая содержит тольо два неизвестных: a
1
и d. После упро-
щений получаем систему
решением оторой являются a
1
= 3, d = 4.
Ответ. a
1
= 3, d = 4.
1. Сумма первоо и пятоо членов арифметичесой прорес-
сии равна , а произведение третьео и четвертоо ее членов
равно . Найдите сумму 17 первых членов прорессии.
2. Найдите арифметичесую прорессию, если известно, что
a
1
+ a
3
+ a
5
= –12, a
1
a
2
a
5
= 80.
3. Сумма трех чисел, являющихся последовательными чле-
нами арифметичесой прорессии, равна 2, а сумма вадратов
этих чисел равна . Найдите эти числа.
4. В арифметичесой прорессии дано: a
p
= q и a
q
= p; най-
дите формулу общео члена прорессии a
n
(p − q).
5. Поажите, что если для положительных чисел a, b, c чис-
ла a
2
, b
2
, c
2
являются последовательными членами арифмети-
a
9
= a
2
· 5,
a
13
= 2a
6
+ 5.
a
1
+ 8d = 5(a
1
+ d),
a
1
+ 12d = 2(a
1
+ 5d) + 5,
4a
1
= 3d,
a
1
– 2d + 5 = 0,
5
3
---
65
72
------
14
9
------

184 Г л а в а 7. Последовательности
20. Последовательность определяется реуррентным соот-
ношением
x
n + 1
= ,
де a > 0 и x > 0. Доажите, что x
n
= .
§ 38. Арифметическая прогрессия
Последовательность, у оторой задан первый член a
1
, а аж-
дый следующий член, начиная со второо, равен предыдуще-
му, сложенному с одним и тем же числом d, называют арифме-
тичесой прорессией. Таим образом,
a
n + 1
= a
n
+ d, n Ý N,(1)
де a
n
— n-й член прорессии, d— разность прорессии. Фор-
мула общео члена арифметичесой прорессии имеет вид
a
n
= a
1
+ d(n – 1). (2)
Сумма n членов арифметичесой прорессии вычисляется по
формулам
S
n
= n, (3)
S
n
= n.(4)
Свойство членов арифметичесой прорессии
. Любой член
арифметичесой прорессии (роме первоо) равен полусумме
равноотстоящих от нео членов:
a
n
= , k < n.(5)
Если k = 1, то формула (4) примет вид
a
n
= . (6)
Арифметичесая прорессия полностью определена, если
известны ее первый член a
1
и разность d.
x
n
x
n
2
2a+()
2x
n
3
a+
-------------------------------- -
n º×
lim a
3
a
1
a
n
+
2
-------------------
2a
1
dn 1–()+
2
--------------------------------------- -
a
nk–
a
nk+
+
2
-----------------------------------
a
n 1–
a
n 1+
+
2
-----------------------------------
§ 38. Арифметическая прогрессия 185
П р и м е р 1. При делении 9-о члена арифметичесой про-
рессии на ее второй член в частном получается 5, а при де-
лении 13-о члена этой прорессии на ее 6-й член в частном по-
лучается 2 и в остате 5. Найти первый член и разность про-
рессии.
Р е ш е н и е. Условие задачи можно записать в виде сле-
дующей системы уравнений:
Используя формулу общео члена арифметичесой прорессии,
приходим системе
оторая содержит тольо два неизвестных: a
1
и d. После упро-
щений получаем систему
решением оторой являются a
1
= 3, d = 4.
Ответ. a
1
= 3, d = 4.
1. Сумма первоо и пятоо членов арифметичесой прорес-
сии равна , а произведение третьео и четвертоо ее членов
равно . Найдите сумму 17 первых членов прорессии.
2. Найдите арифметичесую прорессию, если известно, что
a
1
+ a
3
+ a
5
= –12, a
1
a
2
a
5
= 80.
3. Сумма трех чисел, являющихся последовательными чле-
нами арифметичесой прорессии, равна 2, а сумма вадратов
этих чисел равна . Найдите эти числа.
4. В арифметичесой прорессии дано: a
p
= q и a
q
= p; най-
дите формулу общео члена прорессии a
n
(p − q).
5. Поажите, что если для положительных чисел a, b, c чис-
ла a
2
, b
2
, c
2
являются последовательными членами арифмети-
a
9
= a
2
· 5,
a
13
= 2a
6
+ 5.
a
1
+ 8d = 5(a
1
+ d),
a
1
+ 12d = 2(a
1
+ 5d) + 5,
4a
1
= 3d,
a
1
– 2d + 5 = 0,
5
3
---
65
72
------
14
9
------

186 Г л а в а 7. Последовательности
чесой прорессии, то числа , , таже являются
последовательными членами арифметичесой прорессии.
6. Сумма и разность членов арифметичесой прорессии по-
ложительна. Если увеличить разность на 2, не меняя первоо
члена, то сумма исходной прорессии увеличится в 3 раза.
Если же разность исходной прорессии увеличить в 4 раза, то
сумма прорессии увеличится в 5 раз. Определите разность ис-
ходной прорессии.
7. Найдите число членов арифметичесой прорессии, у о-
торой отношение суммы первых 13 членов сумме последних
13 равно , а отношение суммы всех членов без первых трех
сумме всех членов без последних трех равно .
При решении задач, в оторых используется понятие суммы
членов арифметичесой прорессии, удобно применять следую-
щую формулу:
a
n + 1
= S
n + 1
– S
n
.(7)
П р и м е р 2. Известно, что при любом n сумма членов не-
оторой прорессии выражается формулой S
n
= 4n
2
– 3n. Най-
ти общий член прорессии.
Р е ш е н и е. Используя формулу (7), имеем
a
n + 1
= S
n + 1
– S
n
= 4(n + 1)
2
– 3(n + 1) – (4n
2
– 3n) = 8n + 1,
a
n
= 8(n – 1) + 1 = 8n – 7.
Ответ. a
n
= 8n – 7.
8. Известно, что при любом n сумма членов неоторой по-
следовательности выражается формулой S
n
= 2n
2
+ 3n. Найди-
те десятый член этой последовательности и доажите, что она
является арифметичесой прорессией.
9. Последовательность чисел 1, 4, 10, 19, ... обладает тем
свойством, что разности соседних членов (последующео и пре-
дыдущео) образуют арифметичесую прорессию 3, 6, 9, ... .
Найдите номер члена последовательности, равноо 15 454.
П р и м е р 3. Найти сумму всех четных двузначных чисел.
Р е ш е н и е. Первое четное двузначное число равно 10, а
последнее равно 98. Используя формулу общео члена арифме-
1
bc+
------------ -
1
ac+
-------------
1
ab+
-------------
1
2
---
4
3
---
§ 38. Арифметическая прогрессия 187
тичесой прорессии при d = 2, a
1
= 10, a
n
= 98, получаем
n = 1 + = 45.
Подставляя это значение n в формулу (3), находим
S
n
= · 45 = 54 · 45 = 2430.
Ответ. 2430.
10. Решите уравнение 2 + 5 + 8 + 11 + ... + x = 155.
11. За изотовление и установу первоо железобетонноо
ольца было уплачено 1000 р., а за аждое следующее ольцо
платили на 200 р. больше, чем за предыдущее. Кроме тоо, по
оончании работы было уплачено еще 4000 р. Средняя стои-
мость изотовления и установи одноо ольца оазалась рав-
ной 2244 р. Сольо олец было установлено?
12. Решите уравнение + + ... + = 3.
13. В арифметичесой прорессии сумма m первых ее членов
равна сумме n первых ее членов (m − n). Доажите, что сумма
ее первых m + n членов равна нулю.
14. Найдите сумму всех четных трехзначных чисел, деля-
щихся на 3.
15. Найдите таую арифметичесую прорессию, в оторой
отношение суммы n первых членов сумме n членов, следую-
щих за ними, не зависит от n.
16. Найдите сумму 50
2
– 49
2
+ 48
2
– 47
2
+ ... + 2
2
– 1.
17. Найдите сумму первых 19 членов арифметичесой про-
рессии a
1
, a
2
, ..., если известно, что a
4
+ a
8
+ a
12
+ a
16
= 224.
18. Найдите a
1
+ a
6
+ a
11
+ a
16
, если известно, что a
1
,
a
2
, ... — арифметичесая прорессия и a
1
+ a
4
+ a
7
+ ...
... + a
16
=147.
19. Найдите последовательность, в оторой сумма любоо чис-
ла членов, начиная с первоо, в 4 раза больше вадрата числа
членов.
20. Доажите, что если S
n
, S
2n
, S
3n
— суммы n, 2n, 3n чле-
нов арифметичесой прорессии, то S
3n
= 3(S
2n
– S
n
).
21. Известно, что для неоторой арифметичесой прорессии
и для неоторой пары натуральных чисел m и n имеет место
равенство = . Доажите, что = .
98 10–
2
--------------------
98 10+
2
-------------------- -
4
9
---
x 1–
x
-------------
x 2–
x
-------------
1
x
---
S
m
S
n
------- -
m
2
n
2
------- -
a
m
a
n
-------
2m 1–
2n 1–
-------------------

186 Г л а в а 7. Последовательности
чесой прорессии, то числа , , таже являются
последовательными членами арифметичесой прорессии.
6. Сумма и разность членов арифметичесой прорессии по-
ложительна. Если увеличить разность на 2, не меняя первоо
члена, то сумма исходной прорессии увеличится в 3 раза.
Если же разность исходной прорессии увеличить в 4 раза, то
сумма прорессии увеличится в 5 раз. Определите разность ис-
ходной прорессии.
7. Найдите число членов арифметичесой прорессии, у о-
торой отношение суммы первых 13 членов сумме последних
13 равно , а отношение суммы всех членов без первых трех
сумме всех членов без последних трех равно .
При решении задач, в оторых используется понятие суммы
членов арифметичесой прорессии, удобно применять следую-
щую формулу:
a
n + 1
= S
n + 1
– S
n
.(7)
П р и м е р 2. Известно, что при любом n сумма членов не-
оторой прорессии выражается формулой S
n
= 4n
2
– 3n. Най-
ти общий член прорессии.
Р е ш е н и е. Используя формулу (7), имеем
a
n + 1
= S
n + 1
– S
n
= 4(n + 1)
2
– 3(n + 1) – (4n
2
– 3n) = 8n + 1,
a
n
= 8(n – 1) + 1 = 8n – 7.
Ответ. a
n
= 8n – 7.
8. Известно, что при любом n сумма членов неоторой по-
следовательности выражается формулой S
n
= 2n
2
+ 3n. Найди-
те десятый член этой последовательности и доажите, что она
является арифметичесой прорессией.
9. Последовательность чисел 1, 4, 10, 19, ... обладает тем
свойством, что разности соседних членов (последующео и пре-
дыдущео) образуют арифметичесую прорессию 3, 6, 9, ... .
Найдите номер члена последовательности, равноо 15 454.
П р и м е р 3. Найти сумму всех четных двузначных чисел.
Р е ш е н и е. Первое четное двузначное число равно 10, а
последнее равно 98. Используя формулу общео члена арифме-
1
bc+
------------ -
1
ac+
-------------
1
ab+
-------------
1
2
---
4
3
---
§ 38. Арифметическая прогрессия 187
тичесой прорессии при d = 2, a
1
= 10, a
n
= 98, получаем
n = 1 + = 45.
Подставляя это значение n в формулу (3), находим
S
n
= · 45 = 54 · 45 = 2430.
Ответ. 2430.
10. Решите уравнение 2 + 5 + 8 + 11 + ... + x = 155.
11. За изотовление и установу первоо железобетонноо
ольца было уплачено 1000 р., а за аждое следующее ольцо
платили на 200 р. больше, чем за предыдущее. Кроме тоо, по
оончании работы было уплачено еще 4000 р. Средняя стои-
мость изотовления и установи одноо ольца оазалась рав-
ной 2244 р. Сольо олец было установлено?
12. Решите уравнение + + ... + = 3.
13. В арифметичесой прорессии сумма m первых ее членов
равна сумме n первых ее членов (m − n). Доажите, что сумма
ее первых m + n членов равна нулю.
14. Найдите сумму всех четных трехзначных чисел, деля-
щихся на 3.
15. Найдите таую арифметичесую прорессию, в оторой
отношение суммы n первых членов сумме n членов, следую-
щих за ними, не зависит от n.
16. Найдите сумму 50
2
– 49
2
+ 48
2
– 47
2
+ ... + 2
2
– 1.
17. Найдите сумму первых 19 членов арифметичесой про-
рессии a
1
, a
2
, ..., если известно, что a
4
+ a
8
+ a
12
+ a
16
= 224.
18. Найдите a
1
+ a
6
+ a
11
+ a
16
, если известно, что a
1
,
a
2
, ... — арифметичесая прорессия и a
1
+ a
4
+ a
7
+ ...
... + a
16
=147.
19. Найдите последовательность, в оторой сумма любоо чис-
ла членов, начиная с первоо, в 4 раза больше вадрата числа
членов.
20. Доажите, что если S
n
, S
2n
, S
3n
— суммы n, 2n, 3n чле-
нов арифметичесой прорессии, то S
3n
= 3(S
2n
– S
n
).
21. Известно, что для неоторой арифметичесой прорессии
и для неоторой пары натуральных чисел m и n имеет место
равенство = . Доажите, что = .
98 10–
2
--------------------
98 10+
2
-------------------- -
4
9
---
x 1–
x
-------------
x 2–
x
-------------
1
x
---
S
m
S
n
------- -
m
2
n
2
------- -
a
m
a
n
-------
2m 1–
2n 1–
-------------------

188 Г л а в а 7. Последовательности
22. При аих значениях параметра a найдутся таие значе-
ния x, что числа , являются тремя
последовательными членами арифметичесой прорессии?
23. При аом значении x числа lg 2, lg lg
являются тремя последовательными членами арифметичесой
прорессии?
24. Доажите, что если u
1
, u
2
, u
3
(u
1
− u
2
) — члены (не обя-
зательно последовательные) арифметичесой прорессии, то
существует таое рациональное число λ, что = λ.
25. Доажите, что числа , , не моут быть членами
(не обязательно соседними) арифметичесой прорессии.
26. Моут ли числа 2; ; 4,5 быть членами арифметичесой
прорессии?
27. Длины сторон четырехуольниа образуют арифметиче-
сую прорессию. Можно ли вписать в нео оружность?
28. Пусть S
n
— сумма n членов неоторой последователь-
ности и известно, что = . Доажите, что для членов этой
последовательности справедливо отношение
= .
§ 39. Геометрическая прогрессия
Последовательность, у оторой задан первый член b
1
− 0, а
аждый следующий, начиная со второо, получается умноже-
нием предыдущео на одно и то же число q − 0, называют ео-
метричесой прорессией. Таим образом,
b
n
= b
n – 1
q,(1)
де b
n
— n-й член прорессии, q— знаменатель прорессии.
Формула общео члена еометричесой прорессии имеет вид
b
n
= (2)
5
1 x+
5
1 x–
,+
a
2
---
25
x
25
x–
+
(2
x
1),–(2
x
3)+
u
3
u
2
–
u
2
u
1
–
-------------------
2 3 5
6
S
n
S
m
------- -
n
2
m
2
------- -
a
n
a
m
-------
2n 1–
2m 1–
-------------------
b
1
q
n 1–
.
§ 39. Геометрическая прогрессия 189
Сумма n членов еометричесой прорессии вычисляется по
формуле
S
n
= (3)
Если | q | < 1, то еометричесую прорессию называют бесо-
нечно бывающей. Предел суммы ее членов, т. е. S = S
n
,
называют сммой бесонечно бывающей еометричесой
прорессии. Он вычисляется по формуле
S = . (4)
Свойство членов еометричесой прорессии
. Квадрат лю-
боо (роме первоо) члена еометричесой прорессии равен
произведению равноотстоящих от нео членов:
= b
n – k
b
n + k
, k m n, k Ý N.(5)
Геометричесая прорессия полностью определена, если из-
вестны ее первый член b
1
и знаменатель q.
П р и м е р 1. Найти четыре последовательных члена ео-
метричесой прорессии, из оторых второй член меньше пер-
воо на 35, а третий больше четвертоо на 560.
Решение. Пусть b
1
, b
2
, b
3
, b
4
— четыре последователь-
ных члена еометричесой прорессии. Условие задачи можно
записать в виде следующей системы уравнений:
Используя формулу общео члена еометричесой прорессии,
перепишем эту систему в виде
(*)
Подставляя выражение b
1
(1 – q) во второе уравнение системы (*),
получаем для q уравнение q
2
= 16, орни отороо равны 4 и (–4).
Теперь из первоо уравнения системы (*) по известным
значениям q = 4 и q = –4 находим соответствующие значения
b
1
=– , b
1
= 7.
Ответ. – , – , – , – ; (7, –28, 112, –448).
b
1
(1 q
n
)–
1 q–
--------------------------- .
n º×
lim
b
1
1 q–
------------ -
b
n
2
b
1
– 35 = b
2
,
b
3
– 560 = b
4
.
b
1
– b
1
q = 35,
b
1
q
2
– b
1
q
3
= 560.
35
3
------
35
3
------
35 4⋅
3
--------------
35 16⋅
3
------------------
35 64⋅
3
------------------

188 Г л а в а 7. Последовательности
22. При аих значениях параметра a найдутся таие значе-
ния x, что числа , являются тремя
последовательными членами арифметичесой прорессии?
23. При аом значении x числа lg 2, lg lg
являются тремя последовательными членами арифметичесой
прорессии?
24. Доажите, что если u
1
, u
2
, u
3
(u
1
− u
2
) — члены (не обя-
зательно последовательные) арифметичесой прорессии, то
существует таое рациональное число λ, что = λ.
25. Доажите, что числа , , не моут быть членами
(не обязательно соседними) арифметичесой прорессии.
26. Моут ли числа 2; ; 4,5 быть членами арифметичесой
прорессии?
27. Длины сторон четырехуольниа образуют арифметиче-
сую прорессию. Можно ли вписать в нео оружность?
28. Пусть S
n
— сумма n членов неоторой последователь-
ности и известно, что = . Доажите, что для членов этой
последовательности справедливо отношение
= .
§ 39. Геометрическая прогрессия
Последовательность, у оторой задан первый член b
1
− 0, а
аждый следующий, начиная со второо, получается умноже-
нием предыдущео на одно и то же число q − 0, называют ео-
метричесой прорессией. Таим образом,
b
n
= b
n – 1
q,(1)
де b
n
— n-й член прорессии, q— знаменатель прорессии.
Формула общео члена еометричесой прорессии имеет вид
b
n
= (2)
5
1 x+
5
1 x–
,+
a
2
---
25
x
25
x–
+
(2
x
1),–(2
x
3)+
u
3
u
2
–
u
2
u
1
–
-------------------
2 3 5
6
S
n
S
m
------- -
n
2
m
2
------- -
a
n
a
m
-------
2n 1–
2m 1–
-------------------
b
1
q
n 1–
.
§ 39. Геометрическая прогрессия 189
Сумма n членов еометричесой прорессии вычисляется по
формуле
S
n
= (3)
Если | q | < 1, то еометричесую прорессию называют бесо-
нечно бывающей. Предел суммы ее членов, т. е. S = S
n
,
называют сммой бесонечно бывающей еометричесой
прорессии. Он вычисляется по формуле
S = . (4)
Свойство членов еометричесой прорессии
. Квадрат лю-
боо (роме первоо) члена еометричесой прорессии равен
произведению равноотстоящих от нео членов:
= b
n – k
b
n + k
, k m n, k Ý N.(5)
Геометричесая прорессия полностью определена, если из-
вестны ее первый член b
1
и знаменатель q.
П р и м е р 1. Найти четыре последовательных члена ео-
метричесой прорессии, из оторых второй член меньше пер-
воо на 35, а третий больше четвертоо на 560.
Решение. Пусть b
1
, b
2
, b
3
, b
4
— четыре последователь-
ных члена еометричесой прорессии. Условие задачи можно
записать в виде следующей системы уравнений:
Используя формулу общео члена еометричесой прорессии,
перепишем эту систему в виде
(*)
Подставляя выражение b
1
(1 – q) во второе уравнение системы (*),
получаем для q уравнение q
2
= 16, орни отороо равны 4 и (–4).
Теперь из первоо уравнения системы (*) по известным
значениям q = 4 и q = –4 находим соответствующие значения
b
1
=– , b
1
= 7.
Ответ. – , – , – , – ; (7, –28, 112, –448).
b
1
(1 q
n
)–
1 q–
--------------------------- .
n º×
lim
b
1
1 q–
------------ -
b
n
2
b
1
– 35 = b
2
,
b
3
– 560 = b
4
.
b
1
– b
1
q = 35,
b
1
q
2
– b
1
q
3
= 560.
35
3
------
35
3
------
35 4⋅
3
--------------
35 16⋅
3
------------------
35 64⋅
3
------------------
