Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

132

УСТОЙЧИВОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ [ГЛ.

(10.10),

реакция системы

будет

неограниченно возрастать:

сю

lirn

z(t

)*=\

|*(т)|£*т

оо,

(10.11)

т.е.

при

невыполнении условия (10.7) автоматическая система

неустойчива. Таким образом,

для

того

чтобы

автоматическая

система

была

устойчива,

необходимо

достаточно,

чтобы

ее

временная

характери-

стика

k(t)

была

абсолютно

интегрируемой.

Вспоминая,

что

свободный процесс

(t)

определяется выра-

жением

x)dx, (10.12)

заключаем,

что

при ограниченном воздействии (10.4)

оо

\2?{t)\<M

\\k(x)\dx

(10.13)

если временная

характеристика

абсолютно интегрируема,

то

при

/-»оо,

(10.14)

а значит,

lim

(10.15)

Отсюда следует, что

устойчивой

системе

свободный

процесс

течением

ере-

мени

стремится

нулю.

Поскольку

реакция системы

z(t)

представляет собой сумму

вынужденного

(t)

свободного

(t)

процессов (8.25),

то в

устойчивой системе

течением времени устанавливается выну-

жденный процесс,

т. е.

{t)-+г*

Ц).

(10.16)

Абсолютная интегрируемость временной характеристики

k(t)

на-

кладывает определенные условия

на

передаточную функцию

К(р).

Из определения передаточной функции

k{i)e-P

(10.17)

10 1]

УСЛОВИЯ

УСТОЙЧИВОСТИ

133

следует очевидное неравенство

\k(x)\\e"'

\dx.

(10.18)

В правой части комплексной плоскости р (рис. 10.1), включая

мнимую

ось

Rep>0,

(10.19)

имеет место неравенство •

|е~е

|<1.

(10.20)

следовательно, из

(10.18)

с учетом

(10.7) получаем

\К(Р)\*

(10.21)

Рис.

10.1

Это неравенство может быть выполнено, только если передаточ-

ная

функция замкнутой системы

К{р)

в правой полуплоскости,

включая мнимую ось, ограничена, т. е. если передаточная функ-

ция

системы не имеет полюсов в правой части плоскости р и на

мнимой

оси (рис. 10.1). Таким образом,

для

того

чтобы

система

автоматического

регулирования

была

устойчива,

необходимо

достаточно,

чтобы

все

по-

люсы

передаточной

функции

замкнутой

системы

имели

бы

отрицательные

действительные

части,

т. е.

были

бы

левыми

Но,

как было показано в § 8.4, полюсы передаточных функ-

ций

(10.22)

представляют собой корни характеристического уравнения

P(p)

(10.23)

получаемого приравниванием знаменателя передаточной функ-

ции

К(р)

нулю.

Поскольку передаточные функции замкнутой

системы по отношению к любым воздействиям содержат в зна-

менателе один и тот же характеристический многочлен

G(p),

то

сделанный выше вывод не зависит ни от точки приложения

внешнего воздействия, ни от точки, в которой рассматривается

величина, характеризующая состояние системы.

134

УСТОЙЧИВОСТЬ

АВТОМАТИЧЕСКИХ

СИСТЕМ

[ГЛ.

Подводя итог сказанному, приходим к следующей формули-

ровке условий устойчивости.

Для

того

чтобы

система

автоматического

регулирования

была

устойчивой,

необходимо

достаточно,

чтобы

все

корни

ее

характеристического

уравнения

были

бы

левыми.

Подчеркнем,

что для суждения об устойчивости систем авто-

матического регулирования нет необходимости в вычислении

корней

характеристического уравнения. Достаточно лишь

уста-

новить

их расположение на комплексной плоскости. Правила,

позволяющие это сделать, минуя вычисление самих корней,

на»

зываюгся

критериями

устойчивости.

Критерии

устойчивости подразделяются на

алгебраические

частотные.

Алгебраические критерии устойчивости позволяют

судить об устойчивости автоматических систем по коэффициен-

там характеристического уравнения. Частотные критерии устой-

чивости позволяют судить об устойчивости автоматических

систем по частотным характеристикам их элементов, которые

могут

быть получены как аналитическим путем, так и экспери-

ментально.

10.2.

Алгебраические

критерии

устойчивости

Рассмотрим характеристическое уравнение системы

G(p)=0.

Оно

может быть записано в виде

G(р)

оР

+ ... +

аь-ip

(а

> 0).

(10.24)

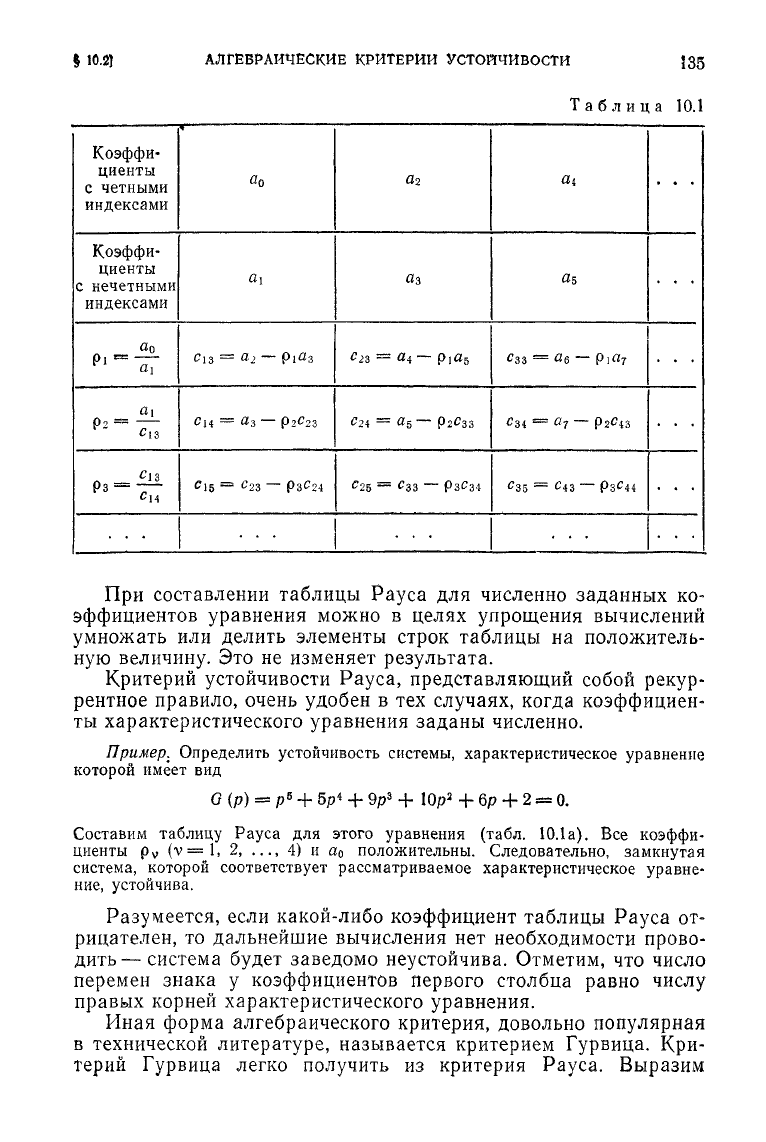
Составим таблицу, называемую

таблицей

Рауса

(табл. 10.1).

В первой и второй строках таблицы Рауса, начиная со второго

столбца, выписываются соответственно коэффициенты с четными

нечетными индексами. Из чисел верхней строки вычитаются

числа нижней строки, предварительно помноженные на такое

число

(v = 1, 2, 3, ...) (оно выписывается в первом столбце),

чтобы первая разность обратилась в нуль. Отбрасывая эту ну-

левую разность, остальные разности выписываются в третьей

строке, начиная со второго столбца.

Для

того

чтобы

система

была

устойчива,

необходимо

достаточно,

чтобы

все

коэффициенты

первого

столбца

таб-

лицы

Рауса

были

положительны,

т. е.

>0,

v=l,

2, ...,

я-1,

(10.25)

или,

что эквивалентно,

> 0,

...,

ft+

, > 0.

(10.26)

Если

хотя

бы

один

из

коэффициентов

характеристического

уравнения

(10.24)

отрицателен,

то

система

неустойчива*

10.2]

АЛГЕБРАИЧЕСКИЕ

КРИТЕРИИ

УСТОЙЧИВОСТИ

J35

Таблица 10.1

Коэффи-

циенты

с четными

индексами

Коэффи-

циенты

с нечетными

индексами

Р2

Рз

Си

с\ь =

—

Pi^3

Си

^2з

^23

—

pia

^24

—

сгз

С2Ъ

—

Рз^з4

сзз

—

Pia

С34

о-?

—

Р2С43

^35

С43

—

Р3С44

. . .

При

составлении таблицы Рауса для численно заданных

ко-

эффициентов

уравнения можно в целях упрощения вычислений

умножать или делить элементы строк таблицы на положитель-

ную величину. Это не изменяет результата.

Критерий

устойчивости Рауса, представляющий собой

рекур-

рентное правило, очень удобен в тех

случаях,

когда

коэффициен-

ты характеристического уравнения заданы численно.

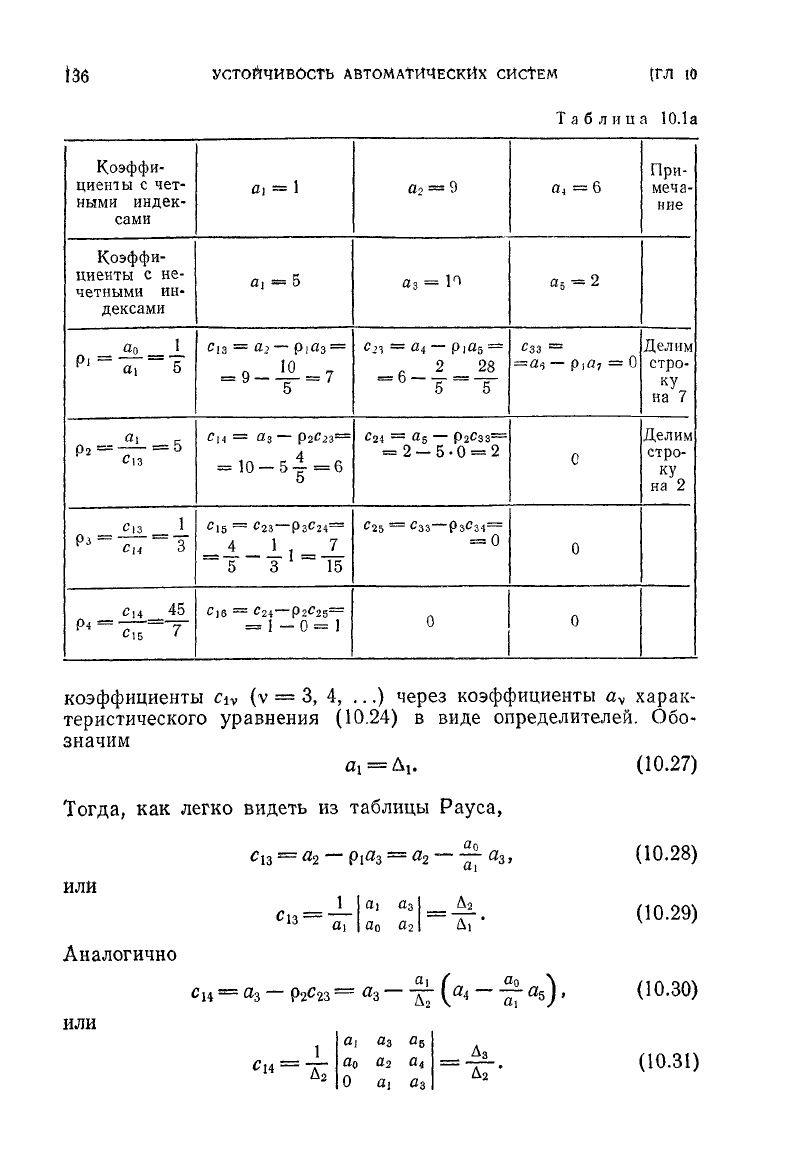
Пример.

Определить устойчивость системы, характеристическое уравнение

которой имеет вид

G (р)

б/?*

9р

+ Юр

+ 6р + 2

«=

Составим таблицу Рауса для этого уравнения (табл. 10.1а). Все

коэффи-

циенты

(v=l, 2, ..., 4) и

положительны. Следовательно, замкнутая

система, которой

соответствует

рассматриваемое характеристическое уравне-

ние,

устойчива.

Разумеется, если какой-либо коэффициент таблицы Рауса от-

рицателен, то дальнейшие вычисления нет необходимости прово-

дить—система

будет

заведомо неустойчива. Отметим, что число

перемен знака у коэффициентов первого столбца равно числу

правых корней характеристического уравнения.

Иная

форма алгебраического критерия, довольно популярная

технической литературе, называется критерием Гурвица. Кри-

терий Гурвица легко получить из критерия Рауса. Выразим

136

УСТОЙЧИВОСТЬ

АВТОМАТИЧЕСКИХ

CHCtEM

[ГЛ

1б

Таблица

10.1а

Коэффи-

циенты

с чет-

ными

индек-

сами

Коэффи-

циенты

с не-

четными

ин-

дексами

«о

—

* —

Рз

-с

с,4

—

pia

—

См

—

02з=

10 —

5—

015

—

РзС24=

""5

3 15

016

s=s

024-~p2025

1^0-

—

pi^s^

2 28

^ 5 ~~ 5

024

—

0зз=

= 2 — 5.0 = 2

025

===

033

—Р3034=

-2

033

=аб~

= 0

При-

меча-

ние

Делим

стро-

на

Делим

стро-

ку

на

коэффициенты

(v = 3, 4, ...) через коэффициенты

харак-

теристического уравнения

(10.24)

в виде определителей. Обо-

значим

£!!

&!.

(10.27)

Тогда, как легко видеть из таблицы Рауса,

*"—

О>2

""*"

Р1

===

""**"

или

Аналогично

—

^23

% —

-д7

~ —

Яб

ИЛИ

п\

пъ

по

0-4

(10.28)

(10.29)

(10.30)

(10.31)

АЛГЕБРАИЧЕСКИЕ

КРИТЕРИИ

УСТОЙЧИВОСТИ

137

Продолжая подобные вычисления далее, получим

-i

—

(10.32)

где

(v=l, 2,

...,

—

диагональные определители, полу-

чаемые

из

матрицы Гурвица

...

0,%

. . .

П]

аз

...

Яд

• •

•

П)

...

(10.33)

Матрица Гурвица составляется по простому правилу: первая

строка заполняется коэффициентами с нечетными индексами, а

вторая

—коэффициентами

с четными индексами. Дальнейшие

пары строк отличаются от первой пары смещением вправо на

один,

два, три и т. д. столбцов. Все коэффициенты с индексами,

большими степени, заменяются нулями.

Критерий

устойчивости

Гурвица

можно сформулировать сле-

дующим образом.

Для

того

чтобы

замкнутая

система

была

устойчивой,

не-

обходимо

достаточно,

чтобы

при

ао

0 все

определи-

тели

Гурвица,

составленные

из

коэффициентов

характери-

стического

уравнения

замкнутой

системы,

были

бы

поло-

жительны,

т. е. чтобы

«1

> 0,

о,

П\

0 а\

-1>0,

-,>0.

(10.34)

Примечание.

Условия устойчивости Гурвица остаются

справедливыми и для характеристического уравнения, записан-

ного в виде

<?i

(Р) =

fl^-ip"-

+ ... +

(10.35)

поскольку корпи этого уравнения

будут

взаимно

обратыы

кор

ням

уравнения (10 24), а это

не

изменяет знака их действитель

шх

частей.

138

УСТОЙЧИВОСТЬ

АВТОМАТИЧЕСКИХ СИСТЕМ

\ГЛ.

Таблица

10.2

оР

{

ajp

+ aip

a2p

-a

о,

Условия устойчивости

> 0,

> 0

> 0,

>0,

Условия

устойчивости для характеристических уравнений при

= 1, 2, 3, 4,

вытекающие

из

(10.34), сведены

табл. 10.2. Из

этой

таблицы следует, что

необходимым

достаточным

условием устойчивости

си-

стемы,

характеристическое уравнение которой первой

или

второй

степени,

является

положительность

всех коэффи-

циентов характеристического уравнения.

Для

систем, характеристические уравнения которых выше

второй

степени, помимо положительности коэффициентов долж-

ны

соблюдаться дополнительные

условия,

которые ограничивают

величину

коэффициентов.

Пример.

Рассмотрим характери-

стическое уравнение третьей степени

G (р)

=====

aip

0. Про-

изведем замену переменной

р =

/——р,

«о

тогда получим р

Ар

Вр

=0, где

Область

неустойчидост

Рис.

10.2.

— Л/

Условия устойчивости, согласно неравен-

ствам табл. 10.2, имеют вид

Л>0,

В>0,

АВ>\.

(10.36)

В системе координат

А, В

область устойчивости располагается выше гипер-

болы

Л£=1.

носящей название гиперболы Вышнеградского (рис,

Ю.£).

10.3]

ЧАСТОТНЫЕ

КРИТЕРИИ

УСТОЙЧИВОСТИ

139

10.3.

Частотные

критерии

устойчивости

Рассмотрим передаточную функцию разомкнутой системы

И^Л^ТПЙ-.

(Ю.37)

или

(10.38)

где

— коэффициент усиления, a

W(p)

—

нормированная

пере-

даточная

функция

разомкнутой системы. Введение нормирован-

ной

передаточной функции позволяет представить разомкнутую

передаточную функцию в виде последовательного соединения

усилителя с коэффициентом усиления k и линейной динамиче-

ской

системы с передаточной функцией

W(p).

Характеристиче-

ское уравнение замкнутой системы G(p) =

(10.23)

получается

приравниванием

суммы полиномов числителя и знаменателя пе-

редаточной функции

W(p)

нулю, т. е.

G (р) = kP (р) +

(р)

= 0.

(10.39)

При

k = 0 из

(10.39)

получаем характеристическое уравнение

разомкнутой системы:

Q(p) = 0.

(10.40)

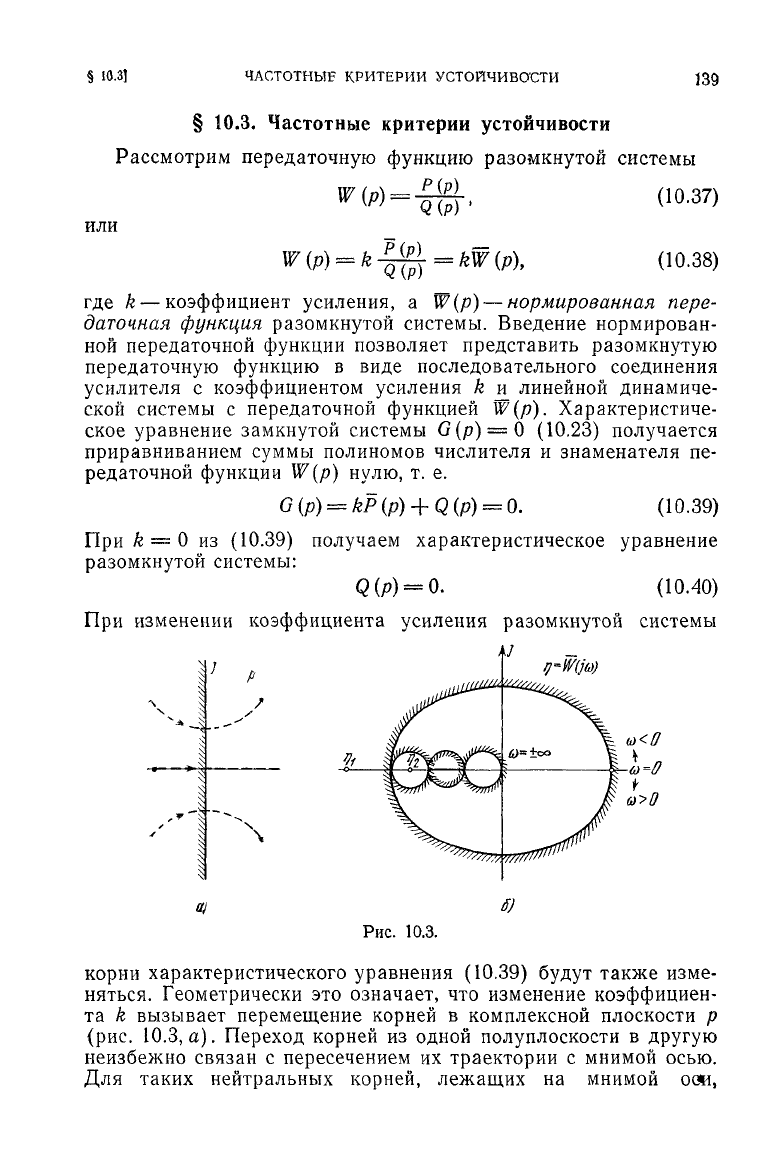
При

изменении коэффициента усиления разомкнутой системы

б)

Рис.

10.3.

корни

характеристического уравнения

(10.39)

будут

также изме-

няться.

Геометрически это означает, что изменение коэффициен-

та k вызывает перемещение корней в комплексной плоскости р

(рис.

10.3, а). Переход корней из одной полуплоскости в

другую

неизбежно связан с пересечением их траектории с мнимой осью.

Для таких нейтральных корней, лежащих на мнимой

ооя,

140

УСТОЙЧИВОСТЬ

АВТОМАТИЧЕСКИХ

СИСТЕМ

[ГЛ. 10

справедливо равенство __

O0'co)

/5P(/(o)

Q(/©)

(10.41)

или

Нормированная

частотная характеристика

W{h)

(10.43)

при

—оо

^ со

оо является отображением на плоскость

г)

мни-

мой

оси /со плоскости переменной р (рис.

10.3,6).

При таком

отображении точки р левой полуплоскости преобразуются в точ-

ки

ц,

лежащие слева от кривой нормированной частотной харак-

теристики

W(j(d)>

а точки р правой

полуплоскости

— в точки

т],

лежащие

_справа

от кривой нормированной частотной характе-

ристики

W(j(d).

Заштрихуем мнимую ось и нормированную

кривую частотной характеристики так, чтобы при возрастании

частоты от

—оо

до оо эта штриховка была слева (рис.

10.3,6).

Предположим, что при каком-либо конкретном вещественном

значении

г\

т^

-г-

уравнение G

(р{)

= 0 имеет

правых кор-

ней;

тогда

для любого

т),

отличного от

TJI,

ЧИСЛО правых корней

сохранится, если переход от

r]i

происходит без пересечения

нормированной

частотной характеристики. Если же при переходе

от

r]i

нормированная частотная характеристика пересекается

с незаштрихованной (с заштрихованной) стороной, то число пра-

вых корней уменьшается (увеличивается) на число пересечений

с незаштрихованной (с заштрихованной) стороной.

Предположим, что разомкнутая система устойчива. Это зна-

чит, что все корни характеристического уравнения

(10.40)

—ле-

вые и, следовательно, число правых корней равно нулю. Харак-

теристическое уравнение разомкнутой системы

(10.40)

получает-

ся

из характеристического уравнения замкнутой системы

(10.39)

при

k = 0, т. е. при

т]

= —

-т-

— оо. Будем увеличивать k от 0,

а значит, и —

-г-

от

—оо.

Замкнутая система при этом остается

устойчивой до тех пор, пока точка —^ не пересечет нормиро-

ванную частотную характеристику

W(/co)

(рис. 10.3). Всякое

пересечение

Щ/со)

с заштрихованной стороны приводит к появле-

нию

у характеристического уравнения

(?(/?)

0 правого

корня,

а пересечение

W(jto)

с незаштрихованной стороны — к устране-

нию

правого

корня.

Число появляющихся и исчезающих правых

корней

равно числу пересекаемых штриховок Отсюда

следует,

что замкнутая система

будет

устойчивой при заданном значении

ko,

если при возрастании

—-г-

от — оо до

—т-

разность

10.3]

ЧАСТОТНЫЕ

КРИТЕРИИ

УСТОЙЧИВОСТИ

141

числа пересечений

W(/co)

с заштрихованной и незаштрихованной

стороны

будет

равна нулю. Поскольку

IF(/co)

при со < 0 пред-

ставляет собой зеркальное отображение нормированной частот-

ной

характеристики

W(jto)

при со > 0, то нетрудно заключить,

что замкнутая система

будет

устойчива при k =

ko,

если норми-

рованная

частотная характеристика

W(ja))

с ростом со либо не

будет

пересекать интервал Г

—оо,

—&™)»

ли

бо

будет

пересе-

кать его снизу вверх и

сверху вниз одинаковое

число

раа.

Назовем пере-

сечения

W (/со) с ростом

со

снизу вверх подъемом, а

сверху вниз — спуском

(рис.

10.4). Тогда замкну-

тая система

будет

устой-

чива, если при возра-

стании

со на интервале

\ Рис 13.4.

1__оо,

—j-\

число

подъ-

емов

(/со)

будет

равно числу спусков и, в частности, эти числа

будут

равны нулю. Очевидно, что это

будет

иметь место тогда и

только тогда, когда нормированная частотная характеристика

не

будет

охватывать точки

—г-.

Поэтому частотный критерий

устойчивости можно сформулировать следующим образом.

Частотный

критерий I

(точечный

критерий). Если

разо-

мкнутая

система

устойчива,

то для

того,

чтобы

замкнутая

система

была

устойчивой,

необходимо

достаточно,

чтобы

нормированная

частотная

характеристика

W(/со)

не охва-

тывала

точку

(

—-

-г-,

Именно

в такой форме частотный критерий устойчивости был

сфорхмулирован

Г. Найквистом.

Поэтому

частотный критерий устой-

чивости обычно называется критерием устойчивости Найквиста.

Если

нас интересует устойчивость замкнутой системы при

значениях коэффициента, принадлежащих интервалу

(г,

ko), т.е.

<С

ko,

то в этом случае частотный критерий устойчивости

удобно сформулировать в следующей форме.

Частотный

критерий II

(отрезковый

критерий). Если

разо-

мкнутая

система

устойчива,

то для

того,

чтобы

замкнутая

система

была

также

устойчивой

при

необхо-

димо

достаточно,

чтобы

нормированная

частотная

ха-

рактеристика

W(j®)

не

охватывала

отрезок

вещественной

/ 1 1 \

оси I —-,

—г-

), не

пересекая

его.