Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

162

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ СИСТЕМ

ГГЛ.

ЩШ

UP)

11.4.

Асимптотические свойства систем, устойчивых

при больших коэффициентах усиления

Поскольку

при

достаточно больших коэффициентах усиления

общее характеристическое уравнение

(11.15)

вырождается

в пре-

дельное

(11.16),

то при

выполнении условий устойчивости свой-

ства системы практически

не

зависят

от

величины коэффициента

усиления

полностью определяются предельной системой, кото-

рой

соответствует предельное характеристическое уравнение

(11.16).

Установим асимптотические свойства, которые прояс-

няют физический смысл подоб-

ных систем.

Как

было выше

установлено

(см. §

11.3),

если

степень передаточной функции

разомкнутой системы

W(p)

больше

2, то

замкнутая систе-

ма обладает граничным

коэф-

фициентом

усиления.

Для

при-

дания

ей

нужных свойств

не-

обходимо путем коррекции,

включения дополнительных

элементов уменьшить степень

передаточной функции

W(p)

так,

чтобы

она

стала меньше

или

равной

двум.

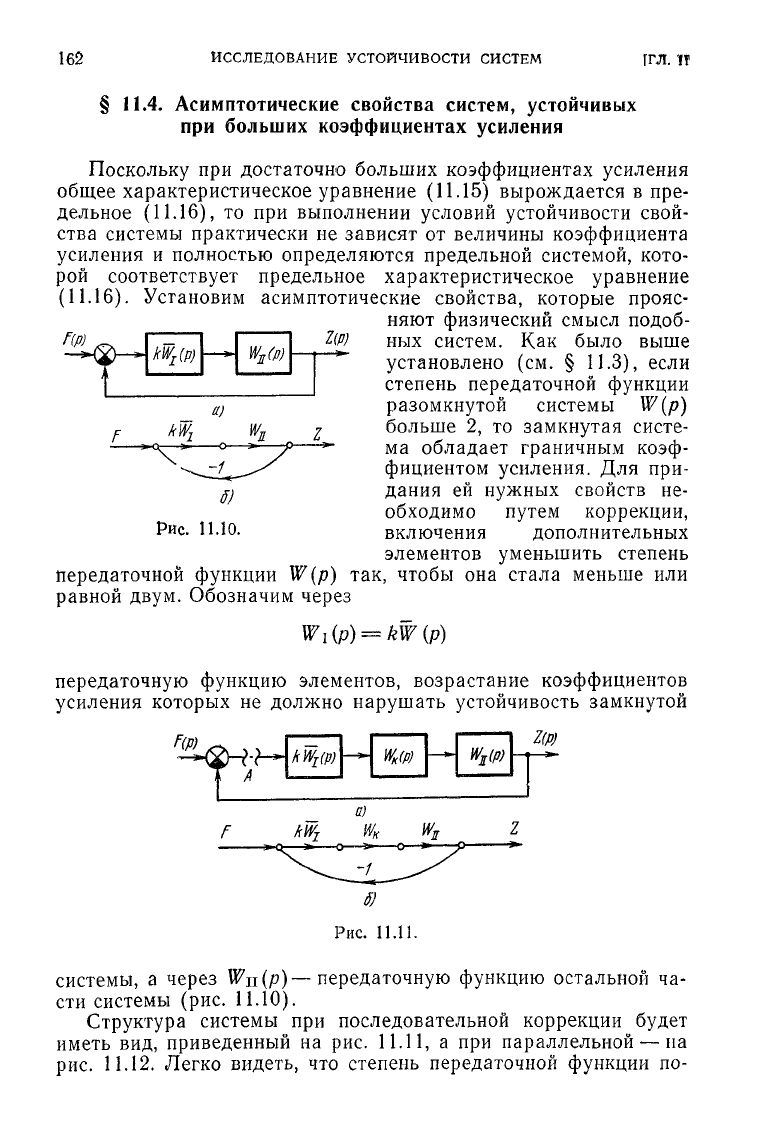
Обозначим через

передаточную функцию элементов, возрастание коэффициентов

усиления которых

не

должно нарушать устойчивость замкнутой

%2н

Z(P)

системы,

через

Wn(p)—

передаточную функцию остальной

ча-

сти системы

(рис.

11.10).

Структура системы

при

последовательной коррекции

будет

иметь

вид,

приведенный

на рис.

11.11,

а при

параллельной

—

на

рис.

11.12. Легко видеть,

что

степень передаточной функции

по-

11.41

АСИМПТОТИЧЕСКИЕ

СВОЙСТВА УСТОЙЧИВЫХ СИСТЕМ

163

следовательного соединения

Wi(p)

(p)

равна

сумме

степеней

передаточных функций:

с2

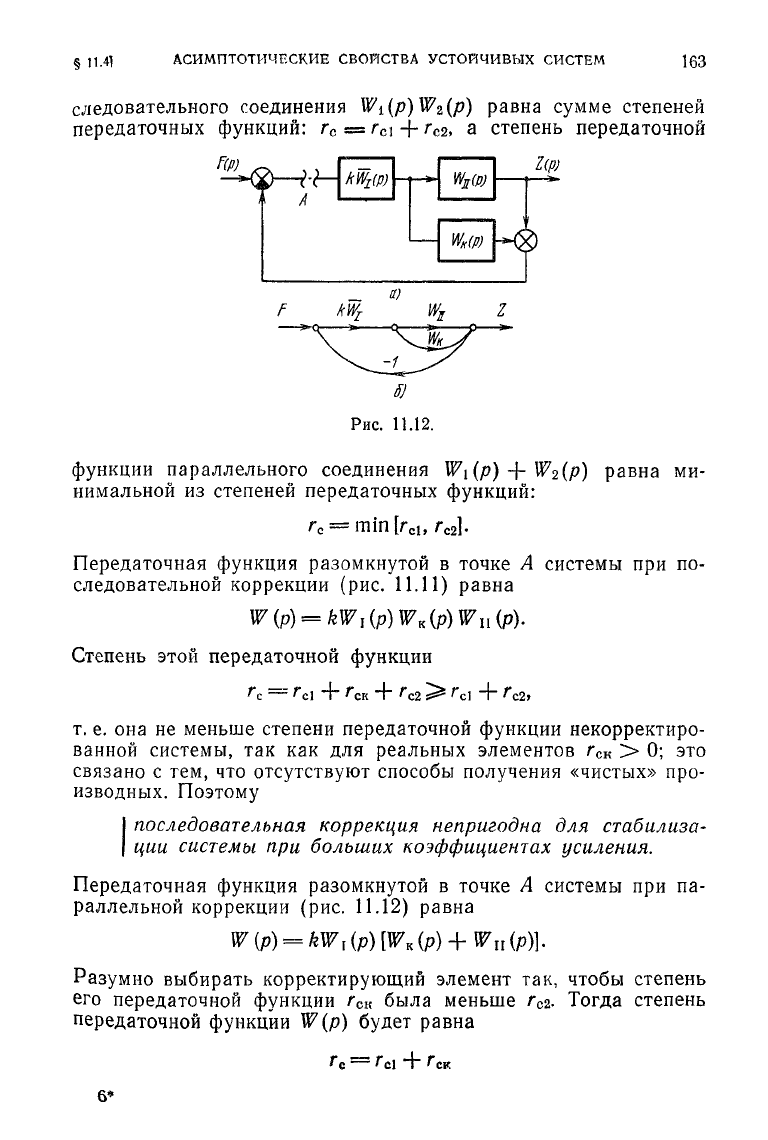
а степень передаточной

Щ(1»

Щи»

функции

параллельного соединения

W\(p)

нимальной

из степеней передаточных функций:

min[r

cl>

равна ми-

Передаточная функция разомкнутой в точке А системы при по-

следовательной коррекции (рис.

11.11)

равна

W(p)

(p)W

(p)-

Степень

этой передаточной функции

===

Гс\

ск

"Т

с2

с\

"Г

^*с2>

т. е. она не меньше степени передаточной функции некорректиро-

ванной

системы, так как для реальных элементов

ск

0; это

связано

с тем, что

отсутствуют

способы получения

«чистых»

про-

изводных. Поэтому

последовательная

коррекция

непригодна

для

стабилиза-

ции

системы

при

больших

коэффициентах

усиления.

Передаточная функция разомкнутой в точке А системы при па-

раллельной коррекции (рис.

11.12)

равна

Разумно выбирать корректирующий элемент так, чтобы степень

его передаточной функции

ск

была меньше

Тогда

степень

передаточной функции

W(p)

будет

равна

164

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ

[ГЛ.

необходимым условием устойчивости при больших

коэффици-

ентах усиления

будет

условие

Гс1

ск

<2;

(11.22)

физически

это условие очевидно.

Наличие

параллельного корректирующего

канала

позво-

ляет

устранить инерционность и

запаздывания,

которые

существовали

в некорректированной системе и были при-

чиной

неустойчивости при больших коэффициентах уси-

ления.

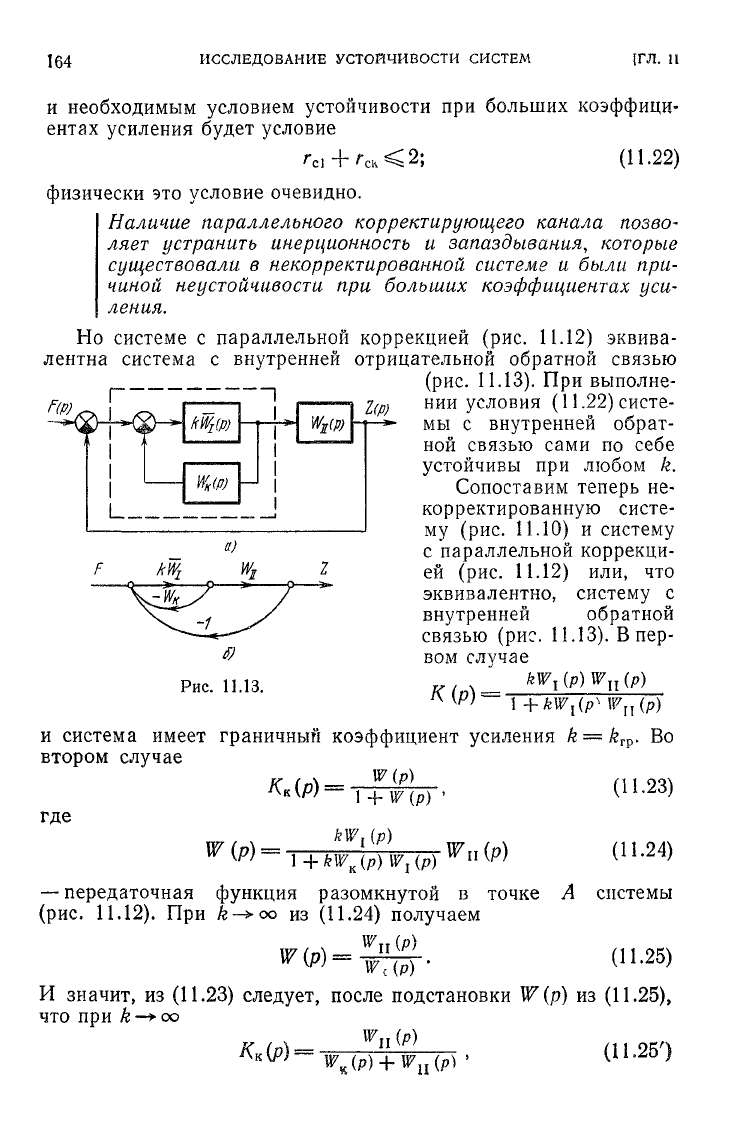
Но

системе

параллельной

коррекцией

(рис. 11.12)

эквива-

лентна

система

внутренней

отрицательной

обратной

связью

______ _

(рис.

11.13).

При

выполне-

F(p)

j~~~

Г"Г~1

[

"П

1(р)

нии

условия

(11.22)

систе-

л л

"•• ""' *• мы с

внутренней

обрат-

ной

связью

сами

по

себе

устойчивы

при

любом

Сопоставим

теперь

не-

корректированную

систе-

му

(рис.

11.10)

систему

параллельной

коррекци-

ей

(рис. 11.12) или, что

эквивалентно,

систему

внутренней

обратной

связью

(рис.

11.13).

В пер-

вом

случае

(p)W

(p)

Щ(Р)

(P)

система имеет граничный коэффициент усиления

Во

втором случае

*-'-*-

W(p)

(11.23)

W(p)

•

где

kWAp)

(11.24)

— передаточная функция разомкнутой в точке А системы

(рис.

11.12).

При

й—>оо

из (11.24) получаем

W{p)=^^

(11.25)

значит, из

(11.23)

следует, после подстановки

(р) из

(11.25),

что

при

^~>оо

(p)

^к

(Р)

ТУТ-ТХЛ-Ш

в25/

)

П.41

АСИМПТОТИЧЕСКИЕ СВОЙСТВА УСТОЙЧИВЫХ СИСТЕМ

165

если

(p)

выбрано так, чтобы все полюсы

(р)

были ле-

выми,

то замкнутая корректированная система, определяемая

передаточной функцией

(11.23),

(11.24)

(рис.

11.12),

будет

устой-

чива при неограниченном возрастании k. Для достаточно боль-

ших k эта система превращается в предельную, или асимптотиче-

скую, систему, соответствующую

передаточной функции

(11.25').

Блок-схема и граф такой предель-

ной

системы изображены на

рис.

11.14. Важно отметить сле-

дующие особенности предельной

системы. Прежде всего, свойства

предельной системы не зависят

от коэффициентов передаточной

функции

Wj(p)

и от коэффициен-

та усиления k, начиная с некото-

рой

величины k >

ko.

Передаточ-

ная

функция разомкнутой в точке А системы (рис.

11.12)

опре-

деляется выражением

(11.25).

Так, при

получаем из

(11.25)

Отсюда следует, что предельная система может приобрести но-

вые свойства, которые отсутствовали в исходной системе.

Введение

корректирующего

элемента,

не

пропускающего

постоянной

составляющей,

придает

системе

свойства

аста-

тичности.

Таким

образом,

системах,

устойчивых

при

большом

коэффициенте

усиле-

ния,

реализуются

свойства

глубокой

отрицательной

обрат-

ной связи:

устранение

влияния

параметров

той

части

си-

стемы,

которая

охватывается

обратной

связью,

обраще-

ние

передаточной

функции цепи

обратной

связи.

Именно

таким путем создают интегрирующие устройства в

аналоговой технике электронного моделирования.

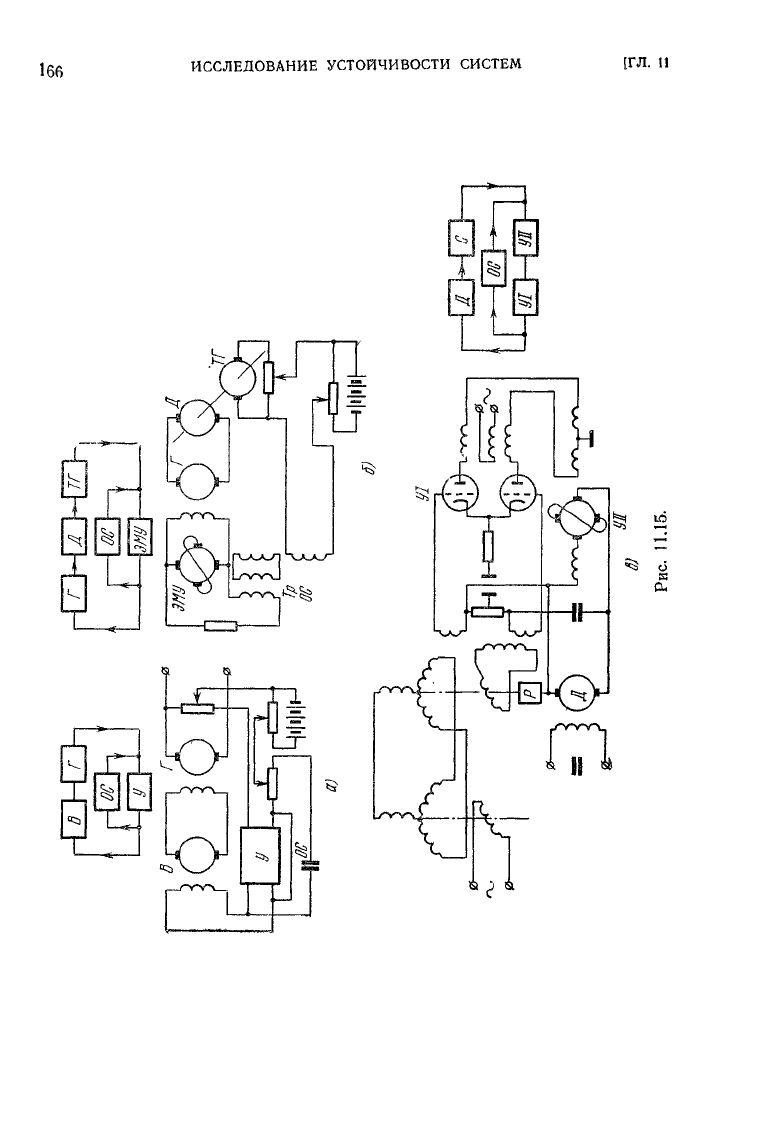
Примеры

систем, в которых используется подобный способ

коррекции,

изображены на рис.

11.15,

— в. Здесь же показаны

блок-схемы этих систем. Обычно передаточная функция кор-

ректирующего элемента выбирается в виде

(11.26).

Нетрудно

видеть,

что выбор передаточной функции корректирующего

166

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ

[ГЛ.

11.5]

УСТОЙЧИВОСТЬ

СИСТЕМ

ЗАПАЗДЫВАНИЕМ

16?

элемента

(p)

це

зависит

от

свойств элементов, характеризуе-

мых передаточной функцией

Wi(p).

Поэтому сделанные здесь

выводы справедливы

и для тех

случаев, когда последние элемен-

ты содержат распределенные параметры, запаздывания

и т. п.

Единственное требование, которому должны удовлетворять

эти

элементы,

— это

устойчивость предельной системы.

11.5.

Устойчивость систем с запаздыванием

До

сих пор

рассматривались системы автоматического

регу-

лирования

сосредоточенными параметрами. Однако

на

прак-

тике часто встречаются системы

распределенными параметра-

ми

и, в

частности,

запаздыванием.

качестве примера такой

Рис.

11.16.

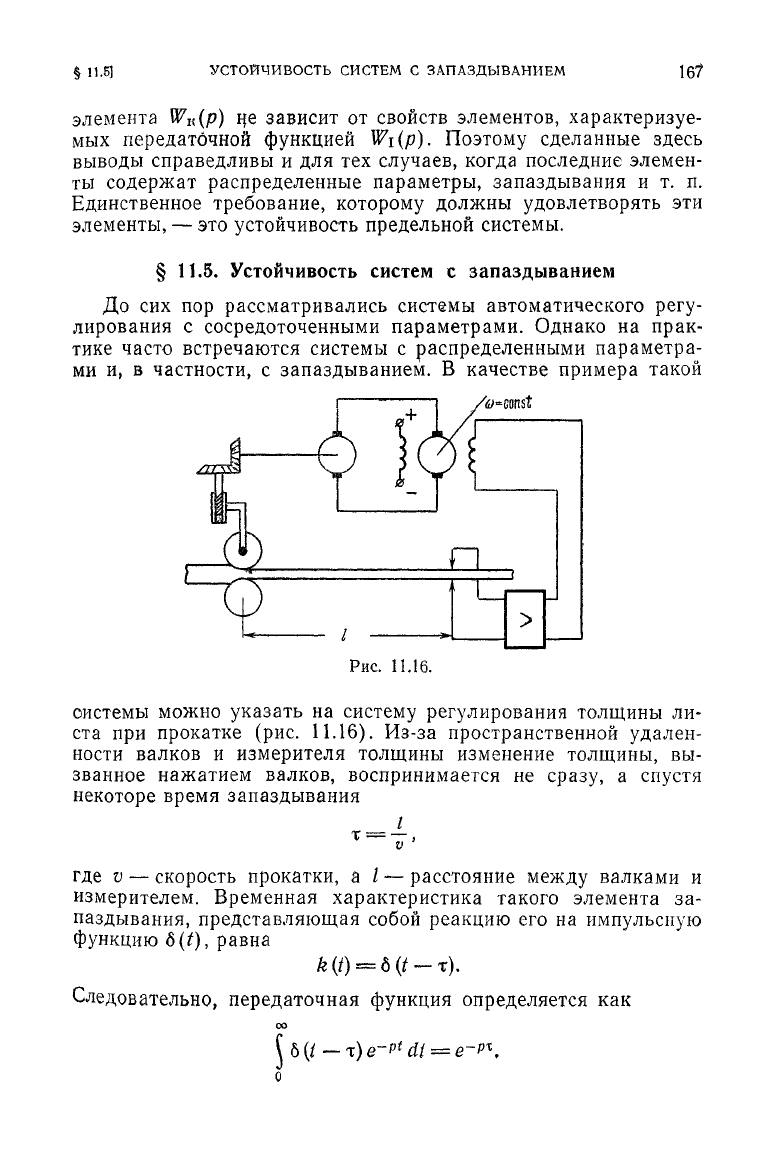
системы можно указать

на

систему регулирования толщины

ли-

ста

при

прокатке

(рис.

11.16).

Из-за пространственной удален-

ности

валков

измерителя толщины изменение толщины,

вы-

званное

нажатием валков, воспринимается

не

сразу,

спустя

некоторе время запаздывания

где

v —

скорость прокатки,

а /

— расстояние

между

валками

измерителем. Временная характеристика такого элемента

за-

паздывания,

представляющая собой реакцию

его на

импульсную

функцию

б(/),

равна

Следовательно, передаточная функция определяется

как

168

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ СИСТЕМ

[ГЛ.

При

p =

j®

получаем частотную характеристику элемента

за-

паздывания

e~~

cos

сот — /

sin

сот.

Она

представляет собой окружность

изображена

на рис.

11.17.

Граф системы

элементом запаздывания приведен

на рис.

11.18.

Передаточная функция разомкнутой системы запишется

виде

(р)

е-^

Цг

(Р)

откуда находим характеристическое уравнение

(11.27)

Это уравнение из-за наличия множителя

e~v

трансцендентно,

поэтому

нему непосред-

ственно неприменимы алге-

браические критерии устойчиво-

сти.

Что же

касается частотно-

го критерия устойчивости,

то

он

применим

и в

этом

случае,

Рис. 11.17. Рис.

11.18.

Частотная характеристика разомкнутой системы

запаздыва*

нием

получается

и при

подстановке

р = /со в

(11.27):

или

поскольку

то

(/со)

(со)

e/[e«D>-«t]

(11.28)

(11.29)

Назовем

частотную характеристику, определяемую выражением

(11.28),

нормированной

предельной

частотной

характеристикой.

Из

(11.29)

видно,

что

наличие запаздывания сказывается

в до-

полнительном сдвиге

фаз.

Благодаря этому радиусы векторов

нормированной

предельной частотной характеристики сдвинуты

на

углы,

равные

—тсо.

Такой сдвиг

фаз

деформирует предельную

частотную характеристику

может привести систему

неустой-

чивости.

На

границе устойчивости

И51

УСТОЙЧИВОСТЬ

СИСТЕМ

ЗАПАЗДЫВАНИЕМ

169

откуда следует, что

или

т==

(со)

—

COT

= — п,

—

(со)

со

(11.30)

(11.31)

Условия

(11.30)

(11.31)

удобно интерпретировать следующим

образом. На плоскости нормированной предельной частотной ха-

рактеристики

Щ/со)

(11.28) проведем окружность радиуса

-j

(рис.

11.19). Точка пересечения этой окружности с

W(/со)

опре-

деляет критическую частоту

при которой выполняется ра-

венство

(11.30).

А предель-

ное

запаздывание определя-

ется, как видно из (11.31),

отношением

запаса по фазе

критической частоте

п —

(со

кр

)

(®кр)

кр

со

кр

со

кр

При

Т,

кр

система устойчива. При

Рис

11.19.

система неустойчива.

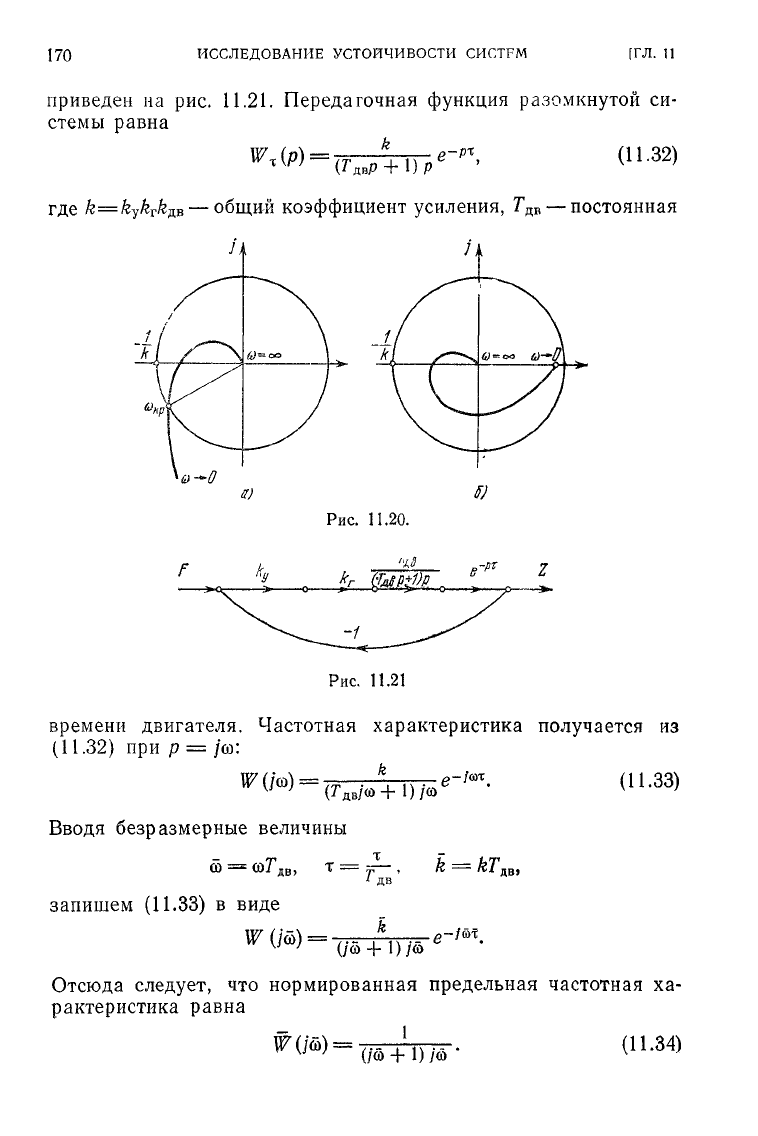
Из

этого критерия устойчивости можно сделать ряд полезных

выводов.

Система,

передаточная

функция

W(p)

которой

обладает

положительным

индексом

апериодической

или

колебатель-

ной

нейтральности,

не

может

быть

устойчивой

при

любом

— она

всегда

имеет

конечное

значение

(рис.

11.20,

а).

Система,

передаточная

функция

которой

обладает

нуле-

вым

индексом

апериодической

колебательной

нейтраль-

ности

при

устойчива

при

любом

т (рис.

11.20,6).

В качестве примера рассмотрим систему регулирования

тол-

щины

прокатываемого металла

(рис.

11.16), граф которой

170

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ

CHCTFM

[ГЛ.

приведен на рис.

11.21.

Передаточная функция разомкнутой си-

стемы равна

-тт-е-

рх

(П-32)

где

kxB

—

общими

коэффициент

усиления,

дв

—

постоянная

Рис.

11.20.

времени двигателя. Частотная характеристика получается из

(11.32)

при р = /со:

Вводя безразмерные величины

дв

запишем

(11.33)

в виде

Отсюда

следует,

что нормированная предельная частотная ха-

рактеристика равна

11.61

УСТОЙЧИВОСТЬ

СИСТЕМ

ЗАПАЗДЫВАНИЕМ

171

Она изображена на рис.

11.22.

Проведя окружность радиуса

-=-,

определяем

со

кр

0(со

кр

)

и, значит,

—•

(со

кр

)

со

кр

можно

определить^

в явной форме. Из уравнений

(11.30)

(11.31)

получаем для W

(jib),

опреде-

, %

ляемой выражением

(11.34),

или

со

+ 1

со

(11.35)

(11.36)

Уравнения

(11.35)

(11.36)

опреде-

ляют параметрическую зависимость т

от

к,

и эту зависимость можно постро-

ить, задаваясь различными значения-

ми

со. Однако эту зависимость можно

Рис.

11.22.

найти и в явной форме, если исклю-

чить из

(11.35)

(11.36)

со. Для этой цели из

(11.35)

получаем

уравнение

Положитель

ьл

корень этого уравнения равен

Подставляя это значение со в

(11.36),

находим

При

1 из

(11.37)

следует

со^лД

, и поскольку

arcig

—

arcig

то из

(11.38)

получаем

(11.37)

(11.38)