Dantzig G., Thapa M. Linear programming. Vol.1. Introduction

Подождите немного. Документ загружается.

232 TRANSPORTATION AND ASSIGNMENT PROBLEM

3 7 11 8

0446

0 4 10 9

1234

Task

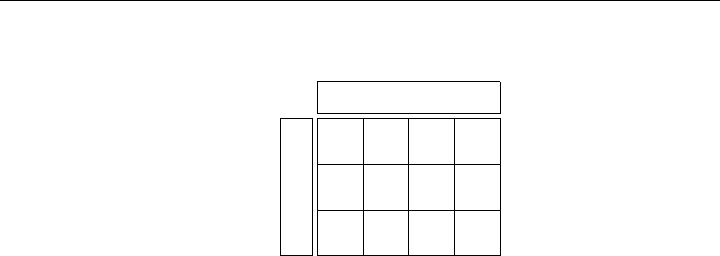
Figure 8-18: Training Cost Data for Assigning 3 Employees to 4 Tasks

a4× 4 assignment array and ﬁnd an initial basic feasible solution by applying Vogel’s

Method as shown in Figure 8-17.

 Exercise 8.28 Compute the simplex multipliers and reduced costs for the problem in

Example 8.17. If not optimal, apply the Transportation Simplex Algorithm to ﬁnd the

optimal solution.

Example 8.18 (Assignment Problem Modiﬁed) Suppose that just before the as-

signments to tasks can be made for the data in Example 8.17, employee number 4 quits.

Management decides to ﬁnd the best possible assignment of the remaining three employees

to three of the tasks, and then, over time, search for a suitable candidate for the fourth

task. The training cost data in this case are shown in Figure 8-18. As set up, the prob-

lem cannot be posed as an assignment problem because we have only three employees to

be assigned to four tasks, whereas we need four employees. However, this can be easily

corrected by setting up a dummy employee, which we shall label by D, and using 0 costs

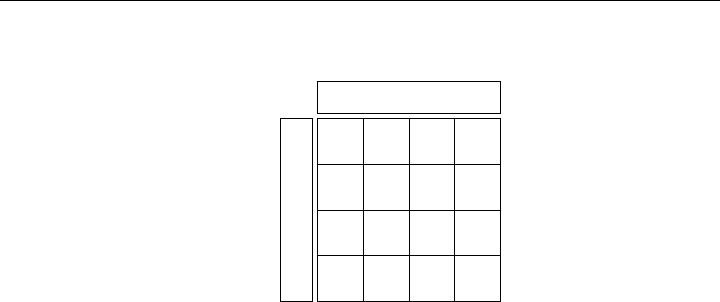
for the assignment of D to any task. The new cost matrix is shown in Figure 8-19.

 Exercise 8.29 Solve the problem posed in Example 8.18.

 Exercise 8.30 Show that setting an arbitrarily high equal cost to every task for the

dummy employee will result in the same optimal assignments but will give a misleading

value to the objective.

 Exercise 8.31 Suppose that employee number 2 informs you that he will not be willing

to take on Task 3. How would you modify the formulation in Example 8.18 to handle this

situation within the context of an assignment problem formulation.

CONVERSION OF A TRANSPORTATION PROBLEM TO AN AS-

SIGNMENT PROBLEM

We have already seen that the assignment problem, is a special case of the trans-

portation problem. It turns out that the transportation problem is a special case

8.6 EXCESS AND SHORTAGE 233

3 7 11 8

0446

0 4 10 9

0000

1234

Task

Figure 8-19: Modiﬁed Training Cost Data for Assigning 3 Employees to 4 Tasks

of the assignment problem as the next exercise demonstrates.

 Exercise 8.32 Assume that a

and b

are integers; if they are rational numbers then

these could be replaced by integers through a change of units. If a

and b

are irrational

numbers, then these could be approximated by rational numbers and then replaced by

integers.

1. Show how to convert the transportation problem into an equivalent assignment

problem by replacing the ith row by a row set I of a

equations each summing to 1,

replacing the jth column by a column set J of b

equations each summing to 1, and

assigning cost c

to all new variables that are in the intersection of row set I and

column set J.

2. Prove that the resulting optimal basic feasible solution to the resulting assignment

problem when aggregated back to the original transportation problem will be an op-

timal feasible solution but need not be a basic solution to the original transportation

problem.

3. Assume that we have solved the transportation problem to obtain an optimal basic

feasible solution. Suppose that the solution is unique (if it is not unique, make it

unique by adding 1 to the nonbasic costs). Show that the solution to the equiva-

lent assignment problem can be used to generate the unique optimal basic feasible

solution to the transportation problem.

8.6 EXCESS AND SHORTAGE

In some applications it may be impossible (or unproﬁtable) to supply all that is

required or to ship all that is available, in which case costs must be given to each unit

not supplied and each unit not shipped from the source. In this section we illustrate

how to formulate and solve such a problem. This problem can be converted to the

234 TRANSPORTATION AND ASSIGNMENT PROBLEM

···

··· ··· ··· ···

···

≤ a

≤···

≤ a

≤

···

≤

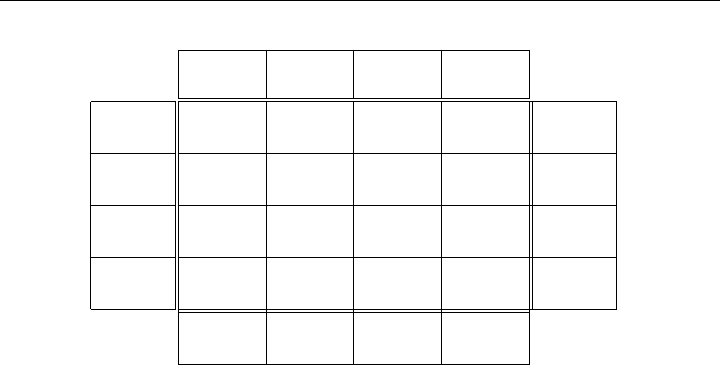
Figure 8-20: Transportation Problem with Inequalities

classical transportation problem by the addition of the slack (excess and shortage)

variables. Other variants of this problem are discussed in Exercises 8.38 and 8.39.

8.6.1 MATHEMATICAL STATEMENT

Aside from its objective, a transportation problem with excess and shortage is of

the form



j=1

≤ a

,i=1,...,m,



i=1

≤ b

,j=1,...,n,

≥ 0,i=1,...,m, j =1,...,n.

(8.24)

This is shown compactly in Figure 8-20.

Example 8.19 (Variation of Prototype Example) Suppose that in the prototype

Example 8.1, which we discussed earlier, we replace the equalities by inequalities of the

“≤” type. Then the problem is to ﬁnd

min z =7x

+2x

+5x

+4x

+3x

+5x

+4x

+1x

+2x

+1x

+3x

+4x

(8.25)

subject to

+ x

≤ 3

+ x

≤ 4

+ x

≤ 5

+ x

≤ 3

+ x

≤ 4

+ x

≤ 2

+ x

≤ 3

(8.26)

8.6 EXCESS AND SHORTAGE 235

···

··· ··· ··· ···

···

= a

= ···

= a

···

Figure 8-21: Transportation Problem with Row and Column Slacks

and x

≥ 0, for i =1,...,3, j =1,...,4.

Introducing slack (excess and shortage) variables x

, the excess at the ith origin,

and x

, the shortage at the jth destination, and letting c

and c

be the positive

penalties for the excesses at the origin and the shortages at the destinations, we

have

Minimize



i=1



j=1



i=1



j=1

= z

subject to x



j=1

= a

,i=1,...,m,



i=1

= b

,j=1,...,n,

≥ 0,x

≥ 0,i=1,...,m, j =1,...,n.

(8.27)

This is shown compactly in Figure 8-21. It should be noted that for problem (8.27)

if there is no penalty associated with failure to deliver the required amounts, then

there is really no problem at all; simply ship nothing. A meaningful problem exists

only when failure to ship means a loss of revenue or goodwill, i.e., when positive

cost factors c

or c

are assigned to the surplus or shortage.

236 TRANSPORTATION AND ASSIGNMENT PROBLEM

8.6.2 PROPERTIES OF THE SYSTEM

RANK OF THE SYSTEM

It is straightforward to see that the addition of slack variables to (8.24) now causes

all m + n equations to be independent, in contrast to the classical transportation

case, in which only m + n − 1 are independent. For example, it is easy to see that

the slack variables constitute a basic set of m + n variables. In fact,

THEOREM 8.7 (Slack in Basis) Every basis contains at least one slack vari-

able.

Proof. Assume on the contrary that some basis has no slack variable. Then

this basis would also constitute a basis for the analogous transportation problem

without any slack variables. This can only happen if



i=1



j=1

. However,

in this case, we know that the number of basic variables cannot exceed m + n − 1;

a contradiction.

 Exercise 8.33 Demonstrate Theorem 8.7 on Example 8.19.

 Exercise 8.34 Suppose that in the classical transportation problem (8.3), all the row

equations are replaced by ≥ and column equations are replaced by ≤ with the condition



i=1



j=1

and arbitrary costs assigned to the surplus and slack variables. Show

that this inequality problem is the same as the original problem. Show that the same is

true if all the inequalities are reversed.

BASIS TRIANGULARITY

THEOREM 8.8 (Basis Triangularity) Every basis is triangular.

 Exercise 8.35 Prove Theorem 8.8.

 Exercise 8.36 Demonstrate Theorem 8.8 on Example 8.19.

8.6.3 CONVERSION TO THE CLASSICAL FORM

The problem (8.27) can be converted to the form of the classical transportation

problem, with an additional rank deﬁciency of 1, by deﬁning



i=1



j=1

, (8.28)

8.6 EXCESS AND SHORTAGE 237

where



i=1



j=1

is the total amount shipped from all origins to all destinations.

From this deﬁnition, it is straightforward to see that



i=1

−



i=1



j=1

−



j=1



i=1



j=1

= x

. (8.29)

Augmenting the transportation problem (8.24) with the slack variables x

and

and using Equation (8.29), we get the classical transportation problem:

Minimize



i=0



j=0

= z, with c

subject to



j=0



j=1



j=0

= a

,i=1,...,m,



i=0



i=1



i=0

= b

,j=1,...,n,

≥ 0,i=0, 1,...,m, j =0, 1,...,n.

(8.30)

This is shown compactly in Figure 8-22.

 Exercise 8.37 Prove that (8.30) has an additional rank deﬁciency of 1 over the classical

transportation problem, i.e., it has rank m + n. Show that adding an arbitrary k =0to



i=1

and to



j=1

in (8.30) increases the rank by 1 to m + n + 1. What conditions

must be placed on k?

 Exercise 8.38 Write down an equivalent classical transportation problem formulation

in equation and array format when there are surpluses only, i.e., when the availabilities

exceed the requirements



i.e.,





but requirements must be met exactly.

 Exercise 8.39 Write down an equivalent classical transportation problem formulation

in equation and array format when there are shortages only, i.e., when the requirements

exceed the availabilities



i.e.,





but all available supplies must be shipped.

 Exercise 8.40 Show that a starting basic feasible solution to (8.30) can be obtained by

choosing as the m+n basic variables the slacks x

for i =1,...,mand x

for j =1,...,n.

Can you think of a better way to get started?

238 TRANSPORTATION AND ASSIGNMENT PROBLEM

···

··· ··· ··· ···

···

= a

= ···

= a



j=1

···



i=1

Figure 8-22: Equivalent Classical Transportation Model

8.6.4 SIMPLEX MULTIPLIERS AND REDUCED COSTS

As in the classical transportation problem case we let u

and v

be the simplex

multipliers (or “implicit prices”) associated with row i column j. Because the rank

of the system is m+n, two of the simplex multipliers can be set arbitrarily. Note that

we need not deﬁne slack multipliers, u

or v

, since there is no equation pertaining

to row zero or to column zero. Hence it is convenient to assign ﬁctitious prices to

these slack multipliers, i.e., u

= 0 and v

= 0. Then the remaining m + n prices

and v

are chosen so that

+ v

= c

if x

is basic. (8.31)

Then the reduced costs are

¯c

= c

− (u

+ v

) for i =0,j =0,

¯c

= c

− v

for j =0, and

¯c

= c

− u

for i =0.

(8.32)

If all the reduced costs for the nonbasic variables are nonnegative, the solution is

optimal.

 Exercise 8.41 Show that the system of equations in u

and v

is triangular.

8.7 PRE-FIXED VALUES AND INADMISSIBLE SQUARES 239

8.7 PRE-FIXED VALUES AND

INADMISSIBLE SQUARES

In practice, it quite often happens that some of the variables must assume pre-

determined values, either 0 or some other ﬁxed values. For example, there may

be no route from an origin i to a destination j in a network; i.e., the variable

must be zero. In the problem of assigning people to jobs, certain assignments

may be mandatory; for example, assigning a physician to a medical position. Sub-

tracting its predetermined value from the corresponding row and column totals it

can be converted to a zero-restricted variable. One way to solve the problem with

zero-restricted variables is to assign an arbitrarily large cost M to these variables

so that if they appear in a feasible optimal basis with a positive value then we

know the original zero-restricted variable problem is infeasible. This is the Big M

method discussed in the Notes & Bibliography section of Chapter 3. For a trans-

portation problem, one way to choose M is to choose it greater than or equal to

max

(i,j)

(



) because



i=1



j=1

≤ max

(i,j)



i=1



j=1

= max

(i,j)





i=1



= max

(i,j)







j=1





Another way to solve such a problem is to shade the cells in the array corre-

sponding to the zero-restricted variables. These shaded cells are called inadmissible

to distinguish them from the regular cells. If only a few cells are inadmissible,

the best practical procedure is to attempt to ﬁnd an initial basic feasible solution

by selecting the next basic variable from among the admissible cells, say, by the

Least-Remaining-Cost rule discussed in Section 8.3.

In the event that the above procedure fails to furnish enough basic variables,

then the zero-restricted variables (or inadmissible cells) can be used to furnish

artiﬁcial variables for a Phase I procedure, in which a basic feasible solution will be

constructed if possible. The Phase I objective of the Simplex Method can be set up

as the infeasibility form

w =



i=1



j=1

, (8.33)

where the d

are deﬁned by



1ifx

is zero-restricted,

0ifx

otherwise.

(8.34)

If a feasible solution exists, then min w is zero; otherwise, if the problem is infeasible,

min w will be positive.

Just as in the solution of a linear program with the Simplex Method, it may

happen that the problem is feasible, but that some inadmissible variables remain in

the basic set at the end of Phase I. Because of the way that the Phase I objective

240 TRANSPORTATION AND ASSIGNMENT PROBLEM

has been deﬁned, we know that these variables will be zero in value, and they must

be kept at zero value throughout the remaining procedure. To do this apply the

starting Phase II rule of the Simplex Method: drop any nonbasic x

from further

consideration if its relative infeasibility factor

= d

− u

− v

is positive, where

and v

are the simplex multipliers associated with the infeasibility form w at the

end of Phase I.

We demonstrate such a Phase I approach in the context of the capacitated

transportation problem, see Example 8.20.

 Exercise 8.42 For the Hitchcock Transportation Problem of Example 8.15, suppose

that x

is invalid. Perform a Phase I approach followed by a Phase II to ﬁnd a new

optimal solution.

8.8 THE CAPACITATED TRANSPORTATION

PROBLEM

A transportation problem with upper bound on the variables is called a capacitated

transportation problem:

Minimize



i=1



j=1

= z

subject to



j=1

= a

,i=1,...,m,



i=1

= b

,j=1,...,n,

0 ≤ x

≤ h

,i=1,...,m, j =1,...,n.

(8.35)

A rectangular array for recording the data and the primal and dual solution of such

a transportation problem is shown in Figure 8-23 for a 3 × 5 case.

THEOREM 8.9 (Optimality Test) A feasible solution x

= x

∗

for the

capacitated transportation problem is optimal if there is a set of implicit prices

= u

∗

and v

= v

∗

, and relative cost factors ¯c

= c

− u

∗

− v

∗

, such that

0 <x

∗

=⇒ ¯c

=0,

∗

=0 =⇒ ¯c

≥ 0,

∗

= h

=⇒ ¯c

≤ 0.

(8.36)

 Exercise 8.43 Prove Theorem 8.9.

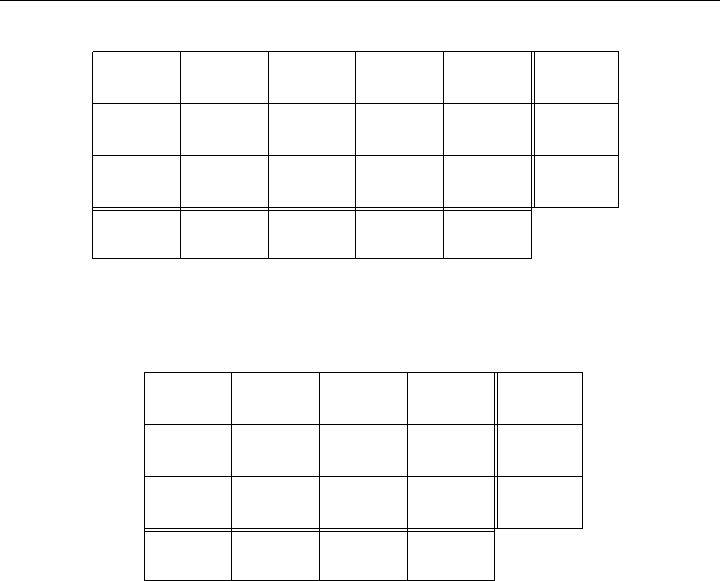
8.8 THE CAPACITATED TRANSPORTATION PROBLEM 241

Figure 8-23: Capacitated Transportation Problem

10567

8276

9348

15 20 30 35

12 13 5 20

14 20 10 9

18 4 25 7

Figure 8-24: Capacitated Transportation Problem Example

The method for solving a transportation problem with upper bounds is an ex-

tension of the method for solving a transportation problem without bounds. While

simple rules have been devised for ﬁnding an initial solution to an uncapacitated

transportation problem, none, to our knowledge, have been found for the capaci-

tated case. If one were able to do this, one could apply it to ﬁnd a simple solution

to the problem of ﬁnding an assignment of m men to m jobs where certain men

are excluded from certain jobs. In mathematical terms, given an m × m incidence

matrix (elements 0 or 1), pick out a permutation of ones or show that none exists.

So far no one has been able to develop a noniterative procedure for solving this

problem.

We shall illustrate an approach for solving a capacitated transportation problem

with the following example.

Example 8.20 (Solution of a Capacitated Transportation Problem) Consider

the capacitated transportation problem in Figure 8-24. In trying to ﬁnd an initial solution

for the problem in Figure 8-24, we begin by selecting a box (cell) with the minimum

, which in Figure 8-24 is c

= 2. Next we assign as high a value as possible to the

corresponding variable, in this case x

, without forcing any variable to exceed its upper