Dantzig G., Thapa M. Linear programming. Vol.1. Introduction
Подождите немного. Документ загружается.


242 TRANSPORTATION AND ASSIGNMENT PROBLEM
10567
8276
9348
25
25
50
15 20 30 35
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
15 25 7
12 13 5 20
14 20 10 9
18 4 25 7
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
......................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.............................................................................................................................................................................................................................................................................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
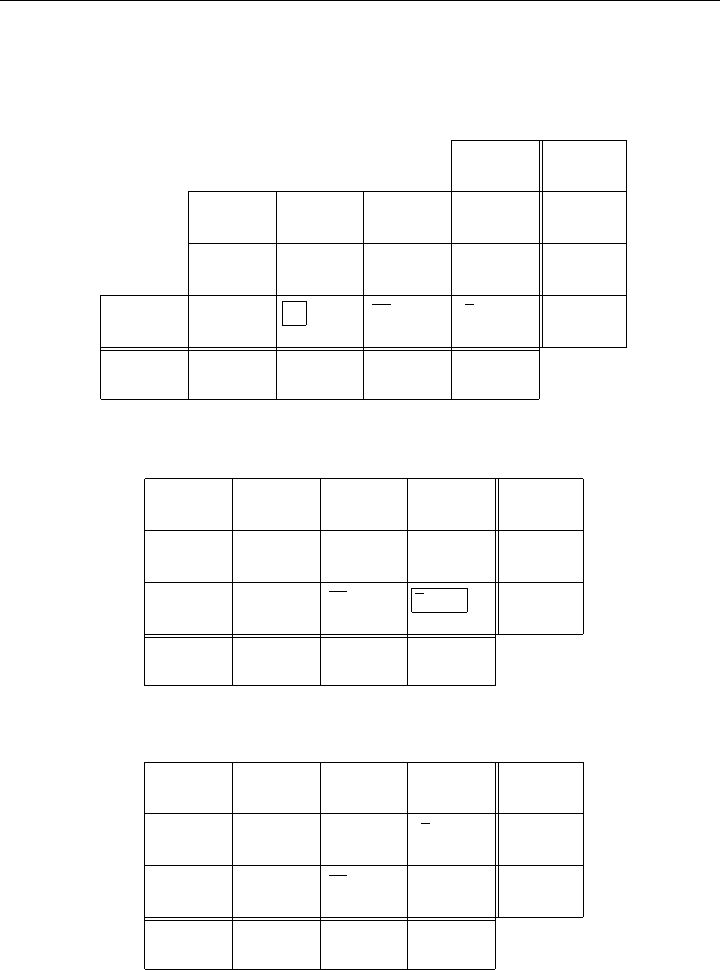
Figure 8-25: Initial Solution of a Capacitated Transportation Problem
bound, that is, we set x
22
= 20. If the value of the variable is limited by a row or column
equation rather than its bound, we consider it to be a basic variable and make no more
entries in its row or column. If, on the other hand, the value of the variable is limited
by its upper bound, then we consider the variable to be nonbasic at its upper bound and
indicate this by putting a bar on the entry. If there is a tie between the two types of
limitations, we always consider the row or column as limiting and consider the variable
basic. Then we repeat the procedure with the remaining boxes.
Application of the above procedure to Figure 8-24 yields, in order, the assignments
x
22
= 20 (basic), x
33
= 25 (bounded), x
13
= 5 (basic), x
24
= 5 (basic), x
14
= 20 (basic),
x
34
= 7 (bounded), x
31
= 15 (basic) as shown in Figure 8-25. Since the third row and
fourth column still have 3 units unassigned, the solution is not feasible. Extra “short”
boxes corresponding to an i = 0 row and j = 0 column are added to the array; the original
c
ij
are replaced by d
ij
= 0, and the shortage boxes have d
ij
= 1 (see iteration 0 of Phase I
in Figure 8-26).
Note that d
30
= d
04
= 1 must equal u
3
and v
4
respectively, since we have previously
shown that slack rows and columns can be regarded as having prices u
0
and v
0
equal to
zero.
Continuing with Phase I, minimizing the sum x
04
+ x
30
of the artificial variables, a
feasible solution is found in one iteration as shown in Figure 8-26. The original cost factors
c
ij
are next restored, as shown in the array for iteration 1 in Figure 8-26.
This solution is not yet optimal, because x
34
is a nonbasic variable at its upper bound
with relative cost factor ¯c
34
=¯c
34
− u
3
− v
4
=8− 0 − 7 = +1. Hence, it pays (except in
degenerate cases) to decrease x
34
from its upper bound value, keeping the other nonbasic
variables fixed and adjusting the basic variables. The greatest decrease θ that maintains
feasibility is θ = 1 because at this value, x
24
reaches its upper bound, i.e., x
24
=8+θ ≤ 9.
The third array in Figure 8-26 is optimal.
The foregoing method illustrated in Example 8.20 implies the following theorem,
whose proof for the general bounded transportation problem is left as an exercise.
8.8 THE CAPACITATED TRANSPORTATION PROBLEM 243
Iteration 0 (Phase I): θ
∗
=3
1
1
0000
0000
0000
0
25
25
50
0 15203035 w =3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
15
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 25 7
θ
∗
12 13 5 20
14 20 10 9
18 4 25 7
0
−1
−1
1
0
−1
111
+2
0
+2
0
−2 −2 −2
u
i
v
j
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
−θ
........................................................................................................................................................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
+θ
−θ
.....................................................................................................................................................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
−θ
Iteration 1 (Phase II): θ
∗
=1
10567
8276
9348
25
25
50
15 20 30 35 z = 552
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
17
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
8
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
15
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 25
7 − θ
∗
12 13 5 20
14 20 10 9
18 4 25 7
0
−1
0
9367
+1 +2
0
+2
−2+1
u
i
v
j
................................................................................................................................................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
+θ
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
−θ
........................................................................................................................................................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
+θ
Iteration 2 (Phase II): Optimal
10567
8276
9348
25
25
50
15 20 30 35
z
∗
= 551
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
16
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
15
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
6
9
25
12 13 5 20
14 20 10 9
18 4 25 7
−1
−1
0
9378
+2 +3
0
+1 −1
−2
u
i
v
j
Figure 8-26: Solution of a Capacitated Transportation Problem

244 TRANSPORTATION AND ASSIGNMENT PROBLEM
THEOREM 8.10 (Integral Property) In a capacitated transportation prob-
lem, if the upper bounds, the availabilities, and the requirements are all integers,
then every basic solution will be integral.
Exercise 8.44 Prove Theorem 8.10.
8.9 NOTES & SELECTED BIBLIOGRAPHY
Many linear programming problems of economic and physical origin can be abstractly
formulated as a network composed of “nodes” (points) connected by “arcs” (routes), over
which various kinds of “flow” (transport) take place (see Chapter 9).
Although he awakened little interest at the time, L.V. Kantorovich [1939] showed that
a class of problems closely related to the classical transportation case has a remarkable
variety of applications concerned typically with the allotment of tasks to machines whose
costs and rates of production vary by task and machine type. He gave a useful but
incomplete algorithm for solving such problems (see the weighted distribution problem,
Chapter 21, in Dantzig [1963]). Again, in 1942, Kantorovich wrote a paper on a continuous
version of the transportation problem, and later, in 1948, he authored an applicational
study, jointly with Gavurin, on the capacitated transportation problem. Dantzig [1951b]
showed how the Simplex Method could be applied to the transportation problem.
The classical transportation problem was first formulated, along with a constructive
solution, by Frank L. Hitchcock [1941]. His paper sketched out an algorithm with points
in common with the Simplex Method; it did not exploit any special properties of the
transportation problem except for finding a starting solution. This paper also failed to
attract much attention.
The shortage of cargo ships during World War II constituted a critical bottleneck.
T.C. Koopmans, as a member of the Combined Allied Shipping Board during World War II,
used properties of the optimal solutions of the transportation problem to help find ways
to reduce overall shipping times. Because of this and the work done earlier by Hitchcock,
the classical case is often referred to as the Hitchcock-Koopmans Transportation Problem.
In 1947, after learning from Dantzig about the proposed use of linear programming for
planning, Koopmans spearheaded the research on linear and nonlinear programs for the
study of problems in economics. His historic paper in 1947, “Optimum Utilization of the
Transportation System,” was based on his wartime experience.
A description of Vogel’s approximation method can be found in Reinfield & Vogel
[1958]. Russel [1969] suggested an alternative approximation method for finding an initial
near-optimal basis for a transportation problem.
See Linear Programming 2 for a very contrived example, due to L. Johnson, of the
occurrence of cycling in the solution process of the transportation problem. It is not
known whether cycling can occur in transportation problems if the entering variable is
chosen based on the usual rule of picking the one that has the most negative reduced
cost. Besides other rules, such as the Random Choice Rule, Bland’s Rule, etc., the simple
perturbation scheme to avoid degeneracy, discussed in Linear Programming 2, can be used
with a trivial amount of extra work.
Another work before the era of linear programming was that of mathematician E. Eger-
v´ary [1931].. His 1931 paper considered the problem of finding a permutation of ones in

8.10 PROBLEMS 245
a square matrix composed entirely of zero and one elements. Based on this investigation,
Kuhn [1955] developed an efficient algorithm (primal-dual), which he called the Hungarian
Method, for solving assignment problems (see Nering & Tucker [1993]). Kuhn’s approach,
in turn, underlies the Ford-Fulkerson Method for solution of the classical transportation
problem (see Chapter 20 in Dantzig [1963]). A detailed survey of assignment problem
algorithms can be found in Ahuja, Magnanti, & Orlin [1989]. In their 1993 book, Ahuja,
Magnanti, & Orlin note that many of the assignment problems share common features; for
example, the successive shortest path algorithm described in their book forms the basis for
many of these algorithms. Bertsekas [1988] has developed an auction algorithm for solving
the assignment problem. Gabow & Tarjan [1989] developed a cost scaling algorithm that
runs in O
m
1
2
n log(mC)
time, where C is the largest cost for any assignment, m is the
number of nodes, and n is the number of arcs. Orlin & Ahuja [1992] also obtain the
same running time of O
m
1
2
n log(mC)
by incorporating scaling within the context of an
auction algorithm.
Computational results for the various specialized algorithms for solving the assign-
ment problem can be found in Bertsekas [1988], Kennington & Wang [1991] and Zaki
[1990]. Computer code listings in the FORTRAN programming language for some of the
algorithms are available in Carpento, Martello, & Toth [1988].
Square arrays of nonnegative numbers x
ij
with the property that all row and all column
sums are unity, frequently appear in statistical theory. They are called doubly stochastic
matrices, and the x
ij
are interpreted as probabilities (not necessarily zero or one). When
such arrays have all x
ij
zero or one, they are called permutation matrices. Garret Birkhoff
[1946] showed that the set of permutation matrices is given by the extreme points of
the convex set defined by the conditions for a doubly stochastic matrix with nonnegative
entries. Von Neumann [1953] establishes Birkhoff’s theorem by reducing an assignment
problem to an interesting matrix game. See also Marcus [1960].
The methods we discussed in this chapter to update the values of the basic variables are
useful for small problems only. To solve large problems on a computer, a more sophisticated
approach for keeping track of and updating basic variables is needed. These techniques are
based on graph-theoretical concepts. Discussion of these methods can be found in Ahuja,
Magnanti, & Orlin [1993], Chv´atal [1983], Glover, Karney, & Klingman [1972, 1973, 1974],
Glover, Karney, Klingman, & Napier [1974], and Murty [1983]. Details about one such
technique is described in Linear Programming 2.
8.10 PROBLEMS
8.1 Consider the transportation array shown below for a problem where the sum of
the supplies is equal to the sum of the demands.
246 TRANSPORTATION AND ASSIGNMENT PROBLEM
534
862
425
768
25
15
a
3
20
40 30
b
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
25
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
15
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
30
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
x
33
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
−1
−3
0
3
425
(a) Show that the values x
33
=2,a
3
= 52, and b
3
= 42 make the given basic
feasible solution optimal.
(b) What values of a
3
and b
3
give a degenerate optimal basic feasible solution?
(c) Why does some u
i
< 0 and other u
i
> 0 not contradict dual feasibility?
(d) Assume a
3
= 60, b
3
= 50, so that x
33
= 10. Is this a unique optimal basic
feasible solution? If so explain why; if not find an alternative optimal basic
feasible solution.
8.2 Omit the primal basic and dual variables and reorder the rows and columns of
Example 8.1 so that the sources are in the order 3, 1, 2, and the destinations
are in the order 1, 2, 4, 3. This results in the following transportation array:
2143
7245
3514
5
3
4
3432
(a) Find an initial solution by randomly applying the general Triangularity
Rule and then solve the problem by hand by the Simplex Algorithm.
(b) Find an initial solution by the Northwest Corner Rule and then solve the
problem by hand by the Simplex Algorithm.
(c) Find an initial solution by the Least-Remaining-Cost Rule and then solve
the problem by hand by the Simplex Algorithm.
(d) Find an initial solution by Vogel’s Method and then solve the problem by
hand by the Simplex Algorithm.
(e) Find an initial solution by Russel’s Method and then solve the problem by
hand by the Simplex Algorithm.
(f) Compare the above five methods. Comment on the numbers of iterations
as compared to those obtained without the reordering.
8.3 Find, an optimal feasible solution to the following transportation problem where
the numbers M mean that shipment is not possible.

8.10 PROBLEMS 247
Week Demand Production Production Storage
Limit cost/set cost/set
1 4 10 20.00 1.00
2 6 25 30.00 1.00
3 10 20 25.00 1.00
4 8 4 40.00 N/A
Table 8-1: Data for Dinner Set Production Schedule
MM 94
4 M 9 M
8 M 35
12MM
6
16
50
14
10 14 28 34
Verify your solution by using the Transportation software option.
8.4 Solve the transportation problem Example 1.5 on Page 4 by the Simplex Method
discussed in this chapter.
8.5 Your wife has recently taken a ceramics class and discovered that she has a
talent for making elegant dinner sets. A specialty store around the corner from
the class has recently sold a couple of sets on her behalf. Besides the fact that
these sets have been well received, the store’s four other suppliers have moved
out of town and the store owner has offered your wife the job of supplying dinner
sets for the next four weeks to meet the store’s demand. With a new baby, it
would be difficult for her to meet the demand on her own. As a result she has
arranged to hire help over the four weeks. The hired help have different skills and
hence different rates. Your wife, on looking over the required demand schedule,
availability of firing time at the ceramics class and the cost of inventory storage
at the class has realized that the problem is nontrivial. She decides to approach
you to see whether your claimed expertise in operations research can help her.
The demand, schedule, and costs are displayed in Table 8-1 You immediately
realize that it can be set up as a linear program. However, on closer examination
you notice that it can be formulated as a transportation problem that can be
solved very efficiently.
(a) Formulate this problem as a transportation problem. Hint: Let x
ij
be the
number of dinner sets produced in week i to satisfy demand in week j.
(b) Solve it by hand.
(c) Solve it by the Transportation software option to verify your solution.
8.6 (a) The optimal solution displayed in Figure 8-14 has ¯c
12
= 0. Demonstrate
a different basic feasible optimal solution in which we bring x
12
into the
248 TRANSPORTATION AND ASSIGNMENT PROBLEM
basis.
(b) How much would the cost of x
11
have to change in the problem of Figure 8-
14 before it becomes a candidate for entering the basis.
8.7 (a) Alternative Optima. For the transportation problem show that alterna-
tive optima exist if ¯c
ij
= 0 for some nonbasic variable x
ij
. Show how to
construct an alternative optimal solution.
(b) Cost Ranging. Derive relations for determining ranges on costs for basic
variables and nonbasic variables that retain optimality of the current solu-
tion of a transportation problem.
(c) Changes in the Right-Hand Side. What is the effect on the optimal solution
of changing a
i
to a
i
+β for some i and correspondingly changing b
j
to b
j
+β
for some j.
8.8 Prove that in the classical transportation problem (u
m
= 0) the values of the
implicit simplex multipliers are always +1 or 0 or −1ifallc
ij
= 0 except that
c
11
= 1. What happens if c
11
= 100.
8.9 (a) For the prototype example solved in Figure 8-14 add 10 to the first column
of costs and solve it. Show that the optimal solution is the same as that
obtained in Figure 8-14.
(b) For the prototype example solved in Figure 8-14 add 5 to the second row
of costs and solve it. Show that the optimal solution is the same as that
obtained in Figure 8-14.
8.10 Consider the transportation problem shown in the following array:
2143
7245
7698
5
3
4
3432
(a) Solve the problem by hand.
(b) Notice that rows 1 and 3 differ by a constant amount equal to 5. Change
the availability of row 1 to be the sum of the availabilities in row 1 and
row 3, drop row 3, and re-solve the problem.
(c) Show that the latter solution is equivalent to the original problem; i.e.,
before the two rows were combined. Show how to obtain the solution to the
original problem from this latter solution to the problem with the combined
rows.
8.11 (a) Prove for the classic transportation problem that the unit costs c
iq
of any
column q can be replaced by c
iq
+ α without affecting the optimal solution;
similarly, for any row r, c
rj
may be replaced by c
rj
+ β.
(b) Prove that the classic transportation problem with some (or all) c
ij
< 0
can be replaced by an equivalent problem where all c
ij
> 0.
8.10 PROBLEMS 249
(c) Suppose corresponding values of c
ij
in two rows differ by a constant; show
that the two rows can be combined into a single row. What happens to the
corresponding variables.
8.12 Consider the transportation problem shown in the following array:
4215
M 721
9 M 6 M
2
7
6
5343
where M implies that shipment is not possible (think of it as a prohibitively
high cost).
(a) Solve the problem by hand using a Phase I / Phase II approach.
(b) Solve it by hand using the Big-M method of Problem 3.28.
(c) Solve it using the Transportation software option to verify your solution.
8.13 Optimal Allocation of Receivers to Transmitters (Dantzig [1963]). A certain en-
gine testing facility is fully using four kinds of instruments: 200 thermocouples,
50 pressure gauges, 50 accelerometers, and 40 thrust meters. Each is measuring
one type of characteristic and transmitting data about it over a separate com-
munication channel. There are four types of receivers, each capable of recording
one channel of information: 200 cameras, 150 oscilloscopes, 256 test instruments
called “Idiots,” and 50 others called “Hathaways.” The setup time per channel
varies among the different types and also according to the kind of data to be
recorded. The allocation table is shown in Figure 8-27, where the setup time
c
ij
is shown in the lower right corner of the square containing x
ij
.
(a) Assuming that all data must be recorded, find an allocation of receivers to
transmitters that minimizes the total setup time.
(b) When recording instruments are in short supply (or are not of the most
suitable types), a decision must be reached as to how much of each kind of
data not to record. The engineers assign the following unit costs assigned
to the shortage row and surplus column.
c
01
=10,c
02
=10,c
03
=4,c
04
= 100,
c
10
=0,c
20
= −1,c
30
=0,c
40
=0, and
c
00
=0.
That is, for example, it is 25 times more costly to neglect thrust data
(c
04
= 100) than to neglect acceleration data (c
03
= 4). In general, however,
it is less costly to record data than to neglect it.
8.14 Consider the following capacitated transportation problem:
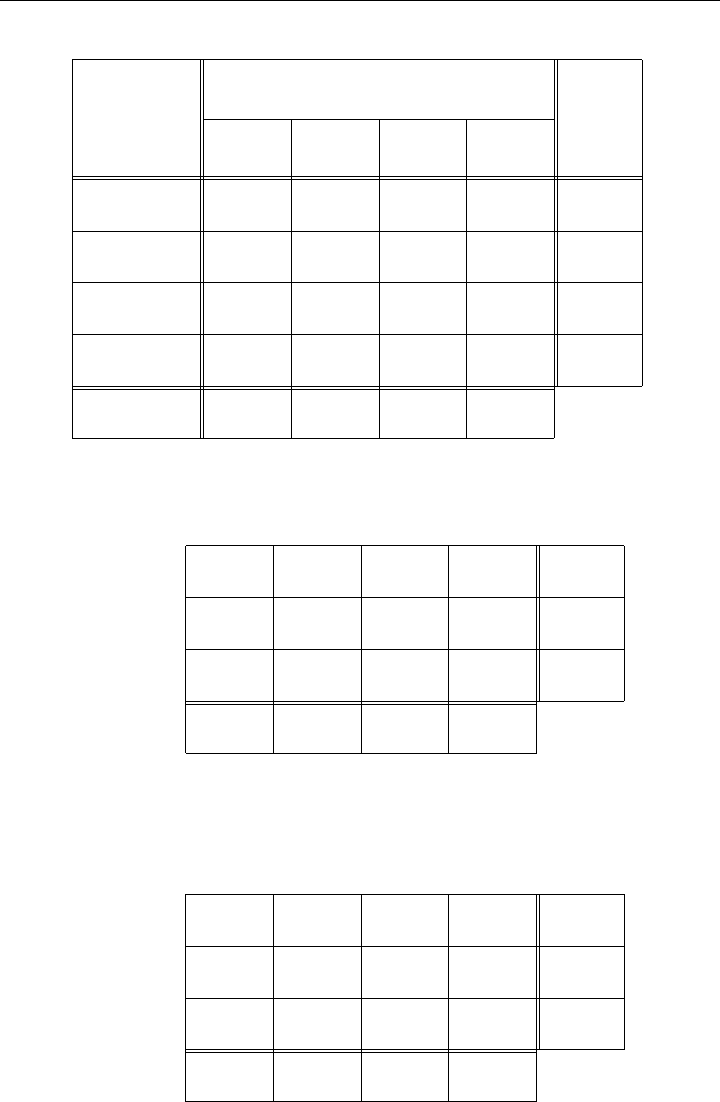
250 TRANSPORTATION AND ASSIGNMENT PROBLEM
13∞ 1
.5 .5 .5 .5
2 2 10 2
1.51.51.51.5
≤ 200
≤ 150
≤ 256
≤ 50
200 50 50 50
x
11
x
12
x
13
x
14
x
21
x
22
x
23
x
24
x
31
x
32
x
33
x
34
x
41
x
42
x
43
x
34
Cameras
1
Oscilloscopes
2
“Idiots”
3
“Hathaways”
4
Total Channels
to be Recorded
Temp.
1
Pressure
2
Accel.
3
Thrust
4
Measuring Instrument
j
Recording
Instrument
i
Total
Recording
Channels
Available
Figure 8-27: Allocation of Receivers to Transmitters
7492
11378
7546
20
30
40
20 25 15 30
x
11
x
12
x
13
x
14
x
21
x
22
x
23
x
24
x
31
x
32
x
33
x
34
8655
15 10 8 10
420 215
(a) Solve the capacitated transportation problem by hand.
(b) Solve it using the Transportation software option to verify your solution.
8.15 Solve the following capacitated transportation problem by hand.
10567
8276
9348
25
25
50
15 20 30 35
x
11
x
12
x
13
x
14
x
21
x
22
x
23
x
24
x
31
x
32
x
33
x
34
5559
14 20 10 9
18 4 25 7
8.10 PROBLEMS 251
Explain how you could have determined in advance that the problem is infeasi-
ble.
8.16 (a) Show for the capacitated transportation problem illustrated in Figure 8-23
that no feasible solution exists if there is a row p such that
n
j=1
h
pj
<a
p
or a column q such that
m
i=1
h
iq
<b
q
.
(b) Construct an example to show that a feasible solution satisfying a capac-
itated transportation problem (see Figure 8-23) need not exist even if for
all i =1,...,m and j =1,...,n
n
j=1
h
ij
≥ a
i
,
m
i=1
h
ij
≥ b
j
.
8.17 Consider the assignment problem shown in the following array:
6241
2572
210
M
7
8
M
75
1234
1
2
3
4
Task
E
m
p
l
o
y
e
e
where M implies that the assignment is not possible.
(a) Solve the above assignment problem by hand.
(b) Solve it using the Transportation software option to verify your solution.
8.18 Find, by hand, a feasible solution to the following 5 × 5 assignment problem
where each person can only be assigned to a subset of available jobs (the exclu-
sion is shown by the letter M):
MMM
MM
MMM
MM
MM
12344
1
2
3
4
5
Job
P
e
r
s
o
n
