Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

422 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

With that, we can initialize the translation versors for each limb L

. We also compute

where their rotation bivectors (the duals of the rotation axes) are in the home position

when expressed in world coordinates relative to the base of the robot. This is done

by simply translating the B

by the successive translation of each joint. The repre-

sentative rendering elements X

are translated in precisely the same manner (we call

the result Y

= 1 T

= T

i−1

−t

∞/2

= T

i−1



i−1

= T

i−1



i−1

This concludes the setup of the robot kinematics parameterization, and allows us to draw

the arm in the gray home position in Figure 14.9.

If the rotation angles ␾

are now speciﬁed at run time, we can compute the rigid body

motion rotors M

for each of the limbs. This merely involves rotating around each of

the rotation bivectors A

by the angle ␾

, and stacking the results for each successive

joint.

You should realize in this that the extension of M

i−1

to M

should be done by a

multiplication on the right by the next rotation around the A

∗

-axis, since that is a

transformation given in the next object frame. The explanation is independent of rotors

and holds in general for the composition of operators. To perform an operator Y (given

in a local frame) when one is in the state X implies that one should undo the present state

rotor X ﬁrst (to get to the proper frame for application of Y), then do Y, and restore the

frame by putting the result at X. Those operations are all performed by the customary left

multiplication (XYX

−1

) X = XY, but the result is equivalent to the right multiplication

of X by Y.

The resulting run-time algorithm is now straightforward:

= 1 M

= M

i−1

−A

␾

= M



We can use the rigid body motions M

to draw the representative elements Z

, giving a

rendering of the moved arm as in Figure 14.9.

The universality of the transformation of the rendering elements X

is the essential differ-

ence with the usual homogeneous coordinate solution. You could also have obtained this

functionality by computing with the homogeneous coordinate matrices throughout and

applying the result as an outermorphism matrix in the ﬁnal equation. In that case, you

would still need to employ the conformal model to make that work on rendering elements

that are not the ﬂats of the homogeneous model.

SECTION 14.6 APPLICATION: KINEMATICS 423

14.6.2 INVERSE KINEMATICS

In computer animation and robotics, inverse kinemat ics is the problem of ﬁnding param-

eters such as angles in a model to make it reach a certain speciﬁed position. Inverse kine-

matics is a notoriously hairy problem in geometrical computation and typically does not

have a unique solution. Depending how it is hinged, each robot need its own speciﬁc

solution to compute its joint angles. Closed solutions are rare, and typically numerical

techniques are used.

The conformal model should be highly suited to represent this problem in Euclidean

geometry, using its capability to compute directly with spatial quantities. Where a clas-

sically speciﬁed solution typically abounds in trigonometric functions because it tries to

ﬁnd a solution in terms of scalars (the angles), geometric algebra can avoid this almost

completely. Instead, it computes spatial rotors by using intersections of spheres and ratios

of lines. Trigonometry is only required if one wants angles as ﬁnal results, and then

involves a logarithm.

Having said that, these techniques have not yet been developed in great generality. To

give a sample of what might be possible, we brieﬂy discuss a very simple robot arm with

a straightforward inverse kinematics algorithm, featuring some of the typical issues in

such problems. The arm is of the humanoid type upper and lower limb, depicted in

Figure 14.10, with limb lengths λ

and λ

. The elbow is a simple planar hinge, but the

shoulder is a spherical joint. With the shoulder ﬁxed, we are asked to reach a target loca-

tion p with the wrist from a standard pose in which the arm is horizontally stretched out

in the e

direction. The limb lengths are given. The principle of the solution we follow is

partly inspired by [34].

We choose our coordinate origin at the shoulder, with e

as the vertical direction.

1. The Tilt Plane. There is an obvious degree of freedom in this problem: we can freely

choose the plane in which we bend the elbow. This tilt plane contains the upper and

lower arm. It certainly needs to contain the line L through shoulder and wrist, which

L = o ∧ p ∧∞.

Therefore it is natural to parameterize the tilt plane by a tilt angle of rotation around

that line. We deﬁne the corresponding tilt rotor R

≡ exp(

∗

␾/2),

where

L denotes the normalized L. To specify the direction of Π

,weneedareference

direction for the tilt plane. Let that be the vertical plane through L (i.e., the plane

= e

∧ L). Then the actual tilt plane is

= R



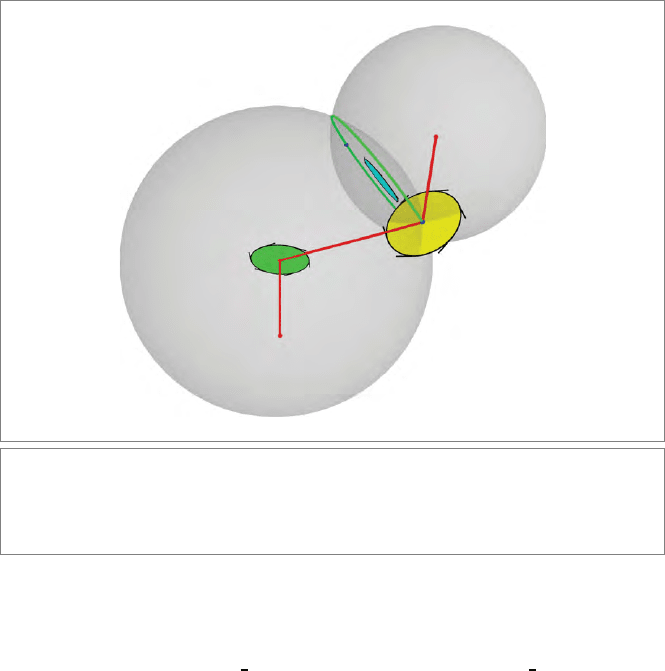
424 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

Base

Shoulder

Right elbow

Wrist

Figure 14.10: A humanoid arm with two movable limbs needs to reach a speciﬁed position

of the wrist. With a choice for the free parameter determining the tilt of the elbow (that rotor

is shown by the light blue tangent bivector), the location of the elbow and the rotors for the

joint angles can be computed using the conformal model (see text).

2. The Elbow Location. The elbow needs to be in the tilt plane at the correct limb

lengths from the shoulder and the wrist. We therefore set up two dual spheres: the

shoulder sphere σ

≡ o −

∞ and the wrist sphere σ

≡ p −

∞. Their dual

meet is the dual circle σ

∧ σ

, and the intersection of that dual circle with the tilt

plane is the elbow point pair P

given by

= (σ

∧ σ

)Π

This gives two possibilities for the elbow. The point pair P

can be split into its two

components P

= p

−

∧ p

by the technique in (14.13). We choose one of those

as the elbow location q. The only concern here is consistency between subsequent

solutions, and that is guaranteed by its automatic sign relationship to the orientation

of the tilt plane.

The intersection may lead to an imaginary point pair. In that case there is no solu-

tion: the robot cannot reach the desired location. Whether this is the case is a simple

test on the sign of P

, which must be nonnegative for a real solution to exist.

SECTION 14.6 APPLICATION: KINEMATICS 425

3. The Elbow Angle Rotor.TheelbowrotorR

is the rotor required to rotate from the

lower arm direction given by the line A = o ∧ q ∧∞to the upper arm direction

B = q ∧ p ∧∞.

We saw in the vector space model that there are several cheap ways of determining a

rotor between two directions (Section 10.3). It is a happy surprise that these meth-

ods all transfer immediately to conformal lines through any point by literal substi-

tution of the lines for the vectors in those equations. They then yield the conformal

rigid body rotor (including translation) to turn one line to the other.

It is not hard to see why this should be so. We consider two lines U and V relative

to their common point x. Then the lines may be represented as U = x ∧ u ∧∞and

V = x ∧ v ∧∞. The constructions to quickly produce a rotor from the two nor-

malized Euclidean directions u and v in Section 10.3 were based on the geometric

product uvand on the squared sum u+v of the two direction vectors u and v. These

quantities are easily computed from the two lines. The geometric product of lines

through the origin is the same as of their directions, for we can factor out the ﬂat

point at the origin: UV= u (o ∧∞)(o ∧∞) v = uv. Also, the sum of the two lines

conveys the sum of the directions U + V = x ∧ (u + v) ∧∞, and geometric ratios

with the square of that quantity therefore also reproduce the vector space results.

We pick the method of the sum of the lines in (10.13) and compute the local elbow

rotor as

1 + VU



2(1 + VU)

(14.12)

This equation is translation-covariant and holds at x = 0, so it is valid everywhere.

It is the rotor of a rotation in the tilt plane, at the elbow q, over the correct angle.

4. Shoulder Rotor. The rotor R

for the shoulder angle of the spherical joint can be

computed in a similar way. We use the two lines along the home position of the

upper arm A

= o ∧e

∧∞and along its computed desired position A = o ∧q ∧∞.

That gives the spherical joint rotor R

by applying a formula such as (14.12). This

rotor resides at the shoulder.

5. Splitting the Spherical Joint. Not every spherical joint controller can handle a rota-

tion in the combined form of simultaneous rotations over its two degrees of free-

dom. In that case, we need to split R

into two rotors.

To be speciﬁc, let us assume that our arm needs to rotate ﬁrst from the home posi-

tion of the lower arm around the vertical axis e

, and then in a vertical plane.

To compute the ﬁrst rotor, we simply compute the projected arm line onto the plane

∗

= o ∧ e

∧ e

∧∞(call it Π

= (AΠ

)/Π

This can also be computed more directly as the rejection (A ∧ e

)/e

. The rotor

from A

to A

is then determined like (14.12). The remaining rotor is R

426 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

determined by the condition that R

= R

, so that R



. This is a rotation

in the plane of the original bivector e

∧ e

, but rotated by R

6. Determining the Angles. All rotors we have determined are centered around their

own points. The corresponding rotation angles follow from the Euclidean part of

their logarithm (13.15), though it is actually more efﬁcient to compute the vector

space logarithm of (10.14) of their Euclidean part. (The outcome is the same, for

taking the Euclidean part is the rejection of the rotor by o ∧∞, which is a covariant

construction).

If this is a robotics problem, you may indeed have to go down to scalar angles to feed

them to the joint controllers. But if this were an animation problem, you should

keep the results in rotor form, for they can be used directly to render the elements

that characterize the limbs in their correct location and attitude.

You see how this solution uses a combination of the capabilities of the conformal model

to compute with offset planes and spheres, and of its natural reduction to the vector space

model at each ﬁxed location.

The implementation of such an algorithm for this particular robot performs about

40 percent faster than the implementation of the classical, angle-based solution [34]. The

main reason for that is partly the avoidance of trigonometry, and partly the avoidance of

representational switching that is typically required within a classical solution between

its several efﬁcient internal representations (from homogeneous coordinate matrices to

quaternions and back, for instance).

14.7 FURTHER READING

The use of circles as elements of computation is not new. A fairly complete treatment may

already be found in 19th century works [9, 10] and a later summary of such techniques

is in the 1941 book by Forder [22]. No one seems to have realized explicitly that the sys-

tem can be extended with Euclidean versors, though they do make obviously covariant

constructions. That breakthrough came in 1999 with [31].

With elements like lines, circles, and rigid body motion rotors as primitives, the conformal

model can be used to describe arbitrary shapes in terms of such descriptors. Rosenhahn

[53, 54] has used this to do model-based tracking. His work is especially interesting for

explicit structural switching between the projective geometry of observation (naturally

described as linear transformations in the homogeneous model) and the desired accurate

Euclidean reconstruction (for which the conformal model is most suited). This stratiﬁ-

cation of geometries is important.

Conformal geometric algebra can be used to perform target calibration in a more direct

way than by iteratively treating translational and rotational components separately as we

did in the vector space model of Section 10.4.2. The ﬁrst results may be found in the work

of Valkenburg et al. [62, 64].

SECTION 14.8 EXERCISES 427

14.8 EXERCISES

14.8.1 DRILLS

These drills intend to familiarize you with the form of common geometric elements and

their parameters in the conformal model. We recommend doing them by hand ﬁrst, and

check them with interactive software later.

1. Give the direct representation of the point pair (0-sphere) P spanned by the points

and p

at location e

and e

, with weights 2 and −1.

2. Compute center and radius of P .

3. Give the dual representation of P, and use it to compute radius and center.

4. Retrieve the locations of the original points from P (see (14.13) below).

5. Compute the carrier line (see Section 15.2.2) of P , both in direct and dual form.

6. Give the direct representation of the circle K through p

, p

, and the unit point at

location e

7. Compute the squared radius and the center of the circle K.

8. Give the direct representation of the sphere Σ through K and the origin.

9. Compute the dual of Σ and read off its center and squared radius directly from that

dual representation.

14.8.2 STRUCTURAL EXERCISES

1. The normalized sphere through four points p, q, r, s is: Σ=(p ∧ q ∧ r ∧ s)/

(p ∧ q ∧ r ∧ s ∧∞)

∗

. Show that the Euclidean vector pointing to the center of this

sphere is

c = (o ∧∞)



o ∧∞∧Σ

∗





(o ∧∞)Σ



夹

Note that the ﬁnal rewriting involves the Euclidean dual. The ﬁrst form is the rejec-

tion of the non-Euclidean parts from the dual. It is easily implemented as simply

listing the Euclidean part of the normalized dual sphere.

2. The weight of a round spanned by four points is related to the volume of the simplex

spanned by those points. Show that the weight of p ∧ q ∧ r/2! is the area of the

triangle pqr, and that the weight of the sphere p ∧ q ∧ r ∧ s/3! is the volume of

the tetrahedron pqrs.

3. Theweightofadualsphereσ is the weight of its center, and equal to ∞·σ. Dualize

this expression to discover when a sphere through the points p, q, r, s becomes zero.

4. In many computations resulting in a point pair P, you would like to have it in the

factorized form P = p

−

∧p

, which is unique apart from scaling. Show that p

and

−

can be computed as:

point pair decomposition: p

P ∓



−∞P

. (14.13)

428 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

(Hint: Simply substitute P = p

−

∧ p

, and develop the terms in the formula; this

shows why the formula works.)

5. For a ﬂat point P = p ∧∞, (14.13) does not work, since it then requires division by

a null vector. In that case, the simplest method is to retrieve the Euclidean position

vector p and use that to make the point p. In an implementation, the coordinates

of p are found as the coefﬁcients of the basis blades e

∧∞, e

∧∞, and e

∧∞,

divided by the coordinate of o ∧∞. Algebraically, show that

p = −

(o ∧∞)(o ∧ P)

(o ∧∞)P

6. Show that the cosine of the angle between two lines L and M through a common

point p can be computed as the usual formula (3.5) directly applied to the lines

themselves rather than to their directions.

7. Compute the

meet of the dual circles κ

= T

[(o −

∞)(−e

)] and κ

= T

−e

[(o −

∞)(−e

)], both residing in the e

∧ e

-plane. It is a tangent vector—what

is its weight, and how is that related to the geometry of the situation?

8. In any of the expressions for the direct or dual directions E∧∞, you can replace the

outer product with a geometric product to write E ∞. Why is a similar substitution

not true for general tangents?

9. In Figure 14.7, the green line segments are part of the Voronoi diagram. The points

of these segments should represent Euclidean circles. Draw these circles in the

Euclidean space. Similarly, the edges of the Delaunay triangulation represent cir-

cles, but they are imaginary. Draw some of those. (For a hint, see Figure 15.8.)

10. Use (3.6) and (3.18) to show that

∞ ∧ X

= −∞X

for general X. (Remember that the squared norm is deﬁned through Y

≡ Y∗



Y .)

11. Extending Figure 14.8, draw pictures displaying the inner product of two spheres

when the center of one is contained inside the other sphere, and when one sphere

is fully contained inside the other sphere.

14.9 PROGRAMMING EXAMPLES AND EXERCISES

14.9.1 VORONOI DIAGRAMS AND DELAUNAY

TRIANGULATIONS

This example uses c2ga (the 2-D conformal model implementation) to compute Voronoi

diagrams and Delaunay triangulations. These geometric constructions were discussed in

Section 14.4. The example lets the user drag 2-D points around, and create new ones.

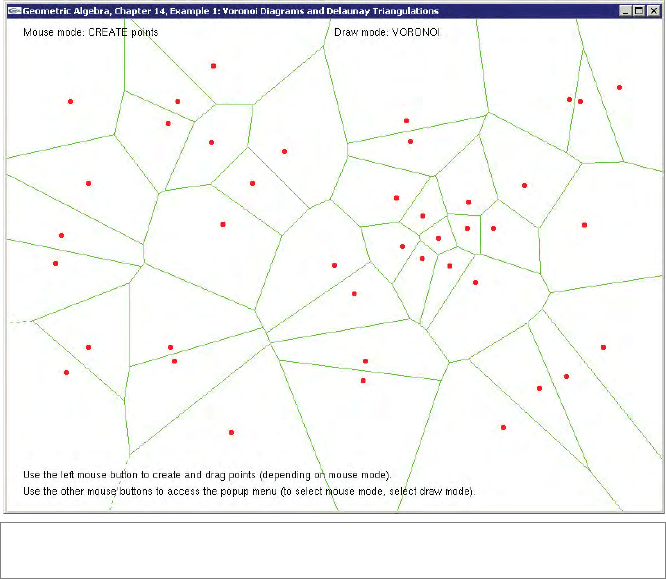
SECTION 14.9 PROGRAMMING EXAMPLES AND EXERCISES 429

Figure 14.11: A Voronoi diagram of a set of points, as computed by Example 1.

The Voronoi diagrams and Delaunay triangulations are updated in real time, using the

following steps:

•

First, the 2-D points (including their ni-coordinate) are passed as a set of 3-D vec-

tors to QHull, an existing library for computing convex hulls. The third dimension

is of course the ∞-direction of the conformal model.

•

The resulting convex hull is stored in a custom data structure called Delaunay-

Triangulation.

•

Backface culling is used to remove the unwanted part of the convex hull.

•

The Voronoi diagram or the Delaunay triangulation is drawn.

We explain each of the steps in more detail below. (Using QHull is a bit backwards, since

QHull itself is able to compute Voronoi diagrams and Delaunay triangulations directly.

However, implementing our own convex hull algorithm just for this example would be

overdoing things.)

430 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

Passing the Points to QHull

QHull does not accept 2-D conformal points as input. So we have to collect the e

-, e

and ∞- coordinates into an array that can be passed to QHull:

// the input points come from this array:

const std::vector<normalizedPoint> &points;

// We store the coordinates in the following array:

// ‘coordT’ is just a floating point type (e.g., float or double)

std::vector<coordT> qhCoord(points.size()*3);

// extract the e1 — , e2 — , ni — coordinates for each point:

for (unsigned int i = 0; i < points.size(); i++) {

qhCoord[i*3+0]=points[i].e1();

qhCoord[i*3+1]=points[i].e2();

qhCoord[i*3+2]=points[i].ni();

}

// pass ‘qhCoord’ to QHull

// ...

Note that p.ni() actually retrieves the ∞-coordinate of a point p, which would alge-

braically be denoted as the operation −o · p, involving

no rather than ni.

Storing the Hull in a DelaunayTriangulation

QHull returns the convex hull as a set of triangles. The vertices of the triangles are the same

points that were originally passed to QHull (i.e., no new points are created). The example

stores the convex hull in a class called

DelaunayTriangulation. This class contains an

array of

DelaunayTriangles, and an array of DelaunayVertexes:

class DelaunayTriangulation {

public:

// ... (Constructors, etc)

std::vector<DelaunayVertex> m_vertices;

std::vector<DelaunayTriangle> m_triangles;

};

Each DelaunayVertex contains a normalizedPoint that speciﬁes its position. Each

DelaunayTriangle contains an array of three vertices and an array of three neighboring

triangles (both speciﬁed by their index). A

DelaunayTriangle also contains a circle

that passes through all three vertices, as described next.

Backface Culling

The convex hull is fully closed, but we do not need the triangles that close the top of the

paraboloid, as these are not part of the Delaunay triangulation. Fortunately, QHull abides

by the counterclockwise-orientation rule for triangles (see Section 2.13.2), so that we can

SECTION 14.9 PROGRAMMING EXAMPLES AND EXERCISES 431

use backface culling to remove the unwanted triangles. Here we compare the orientation

of the circles spanned by the vertices of each triangle to the free bivector e

∧ e

∧∞:

// ’DT’ is a DelaunayTriangulation

// get the vertices of the triangle:

DelaunayVertex &V1 = DT.m_vertices[vtxIdx[0]];

DelaunayVertex &V2 = DT.m_vertices[vtxIdx[1]];

DelaunayVertex &V3 = DT.m_vertices[vtxIdx[2]];

// Check if ‘front-facing’:

// 1: Compute the circle spanned by the three vertices:

circle C = _circle(V1.m_pt ^ V2.m_pt ^ V3.m_pt);

// 2: Compare orientation:

if (_Float(C << (e1 ^ e2 ^ ni)) < 0.0)

continue; // do not use this triangle

// else: this triangle is valid

The circle C is stored along with each triangle for later use; the center point of the circle is

a vertex of the Voronoi diagram.

Drawing the Result

Drawing the Delaunay triangulation from a DelaunayTriangulation is straight-

forward. Drawing the Voronoi diagram is less so. First, we need to ﬁnd the neighbors

of every Delaunay triangle, on a per-edge basis. This is computed when the

DelaunayTriangulation is initialized and stored in each DelaunayTriangle. With

this information available, drawing the Voronoi diagram is done by connecting the cen-

ter points of neighboring triangles with line segments. For each edge that does not

have a neighboring triangle, we draw a (dashed) line from the center point through the

midpoint of the edge.

14.9.2 EXERCISE: DRAWING EUCLID’S ELEMENTS

This example provides the bare-bones code to draw Euclid’s elements (i.e., all ﬂat, round,

free, and tangents blades of the conformal model). It is your job to ﬁll in the code that cre-

ates a typical element of each class and grade. You’ll have to give each element the appro-

priate size and orientation, such that the end result looks somewhat like Figure 14.12.

Note that you could copy the coordinates directly from the ﬁgure, but then you might as

well go straight to the solution that is provided with the GA sandbox source code package.

An example of the code you have to complete is

name = "flat point";

X = no; // < — EXERCISE: insert correct primitive (flat point) here