Ещин Е.К. Моделирование систем управления электромеханическими объектами
Подождите немного. Документ загружается.

121
При формировании частоты тока статора в соответствии с
r
n
cr
n
p
M
C
J
R
p
2
1
3
2
Ψω
+
±
+
ω
ω
=α
имеем:
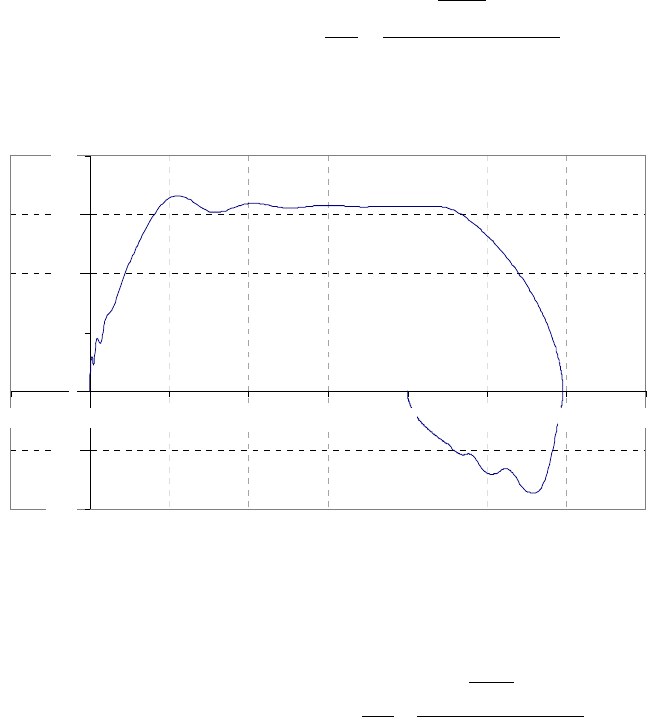
Позиционирование АД
-100
-50
0
50
100
150
200
-10 0 10 20 30 40 50 60 70
Угол поворота ротора, рад
Скорость вращения,1/С
Характер изменения электромагнитных моментов изображен на следующих рисунках, соответственно,
для:
α=±1;
.
p
M
C
J
R
p
r
n
cr
n
2
1
3
2
Ψω
+
±
+
ω
ω
=α
122
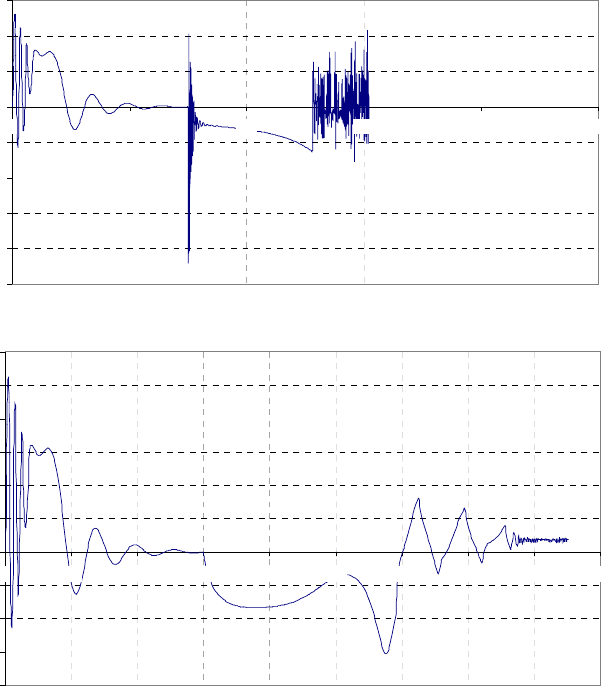
Скользящий режим при позиционировании АД
-1000
-800
-600
-400
-200
0
200
400
600
0 0.2 0.4 0.6 0.8 1
t,C
M,Hm
-400
-300
-200
-100
0
100
200
300
400
500
600
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
t,C
M,Hm
Ниже приведен текст исходного модуля на Visual Basic для среды Excel реализующего задачу по-
зиционирования асинхронного электродвигателя:
' Учебные задачи кафедры ВТ
'===========================================================
' Управление процессом позиционирования
' асинхронного электродвигателя
'============================================================
Option Explicit
Public j, N, i As Integer
Public Y0(), Y0I(), Yz(), Y0z(), _
Y(), F(), _
k1(), k2(), _
k3(), k4() As Single
Public x, X0z, X0, _
Xk, h, Hz, _
eps As Single
Public Rs, Rr, Xs, Xr, Xm, _
l1, l2, lm, w, _
lps, lpr, ks, kr, _
p, GD2, c, Tvn, Tvu, _
alfa, Mc, K, G, A As Single
123
Sub AD()
Dim Prom As Single
Dim Mess As String
A = 40
K = 0.005
N = 6
ReDim Y0(N), Y0I(N), Yz(N), Y0z(N), _
Y(N), F(N), _
k1(N), k2(N), k3(N), k4(N)
Mess = MsgBox("Управление электромагнитным моментом АД", , _
" Учебные задачи кафедры ВТ (Ещин Е.К.)")
eps = 0.0001: h = 0.002: Hz = h
X0 = 0: X0z = X0: h = Hz: Xk = 1
For i = 1 To N
Y0(i) = 0
Next i
Y0(5) = 0.0001
'=========================================================
Tvu = 0.3 ' Время включения управления состоянием АД
'=========================================================
' Параметры для двигателя ВРП160М4
Rs = 0.516: Rr = 0.406
Xs = 1.419: Xr = 1.1
Xm = 35: p = 2
GD2 = 0.7
' Коэффициенты для уравнений движения АД
l1 = Xs / 314
l2 = Xr / 314
lm = Xm / 314
lps = l1 + l2 * lm / (l2 + lm)
lpr = l2 + l1 * lm / (l1 + lm)
ks = lm / (lm + l1)
kr = lm / (lm + l2)
c = 3 * p * ks / (2 * lpr)
Shet ' Основная обработка и подготовка данных
With Sheets("Лист3")
End With
MsgBox "Все!"
End Sub
'=========================================================
Sub Shet()
Dim L, K, R As Integer
Worksheets("Лист3").Select
Worksheets("Лист3").Range("A1: H2000").Clear
j = 2
With Worksheets("Лист3")
For K = 1 To N
.Cells(1, K + 1) = Y0(K)
Next K
End With
x = X0: G = 0
While Sqr(Y0(5) ^ 2 + (Y0(6) - A) ^ 2) > G * 0.01
124
Runge (x)
For i = 1 To N: Yz(i) = Y(i): Next i
h = h / 2
Runge (x)
For i = 1 To N: Y0(i) = Y(i): Next i
x = x + h
Runge (x)
L = 0
For i = 1 To N
If Abs(Yz(i) - Y(i)) < eps * Abs(Yz(i)) Then
L = L + 1
End If
Next i
If L = N Then
With Worksheets("Лист3")
For K = 1 To N
.Cells(j, K + 1) = Y(K)
Y0(K) = Y(K)
Y0z(K) = Y(K)
Next K
.Cells(j, 1) = x
.Cells(j, 8) = .Cells(j, 6)
.Cells(j, 9) = alfa
.Cells(j, 10) = c * (Y(3) * Y(2) - Y(1) * Y(4))
End With
x = x + h
h = Hz
j = j + 1
Else
x = x - h
End If
Wend
End Sub
'=========================================================
Sub Uravnen()
' Формирование управляющего воздействия
If x <= Tvu Then
alfa = 1
G = 0
Else
G = 1
' Определение нахождения фазовой точки и формирование управления
If Y(5) > 0 And Y(6) > 0 Then
alfa = -1
End If
If Y(5) > 0 And Y(6) < 0 And Y(6) >= A - K * Y(5) ^ 2 / 2 Then
alfa = -1
End If
If Y(5) > 0 And Y(6) < 0 And Y(6) < A - K * Y(5) ^ 2 / 2 Then
alfa = 1
End If
'----------------------------------------------------------
If Y(5) < 0 And Y(6) < 0 Then
alfa = 1
End If
If Y(5) < 0 And Y(6) > 0 And Y(6) <= A + K * Y(5) ^ 2 / 2 Then
alfa = 1

125
End If
If Y(5) < 0 And Y(6) > 0 And Y(6) > A + K * Y(5) ^ 2 / 2 Then
alfa = -1
End If
End If
F(1) = 537 * alfa - Rs / lps * Y(1) + Rs / lps * kr * Y(3) + 314 * alfa * Y(2)
F(2) = -Rs / lps * Y(2) + Rs / lps * kr * Y(4) - 314 * alfa * Y(1)
F(3) = -Rr / lpr * Y(3) + Rr / lpr * ks * Y(1) + (314 * alfa - p * Y(5)) * Y(4)
F(4) = -Rr / lpr * Y(4) + Rr / lpr * ks * Y(2) - (314 * alfa - p * Y(5)) * Y(3)
F(5) = 4 * (c * (Y(3) * Y(2) - Y(1) * Y(4))) / GD2
F(6) = Y(5)
End Sub
'=========================================================
Sub Runge(x As Single)
x = X0
For i = 1 To N: Y(i) = Y0(i): Next i: Uravnen
For i = 1 To N: k1(i) = h * F(i): Next i
x = X0 + h / 2
For i = 1 To N: Y(i) = Y0(i) + k1(i) / 2: Next i: Uravnen
For i = 1 To N: k2(i) = h * F(i): Next i
For i = 1 To N: Y(i) = Y0(i) + k2(i) / 2: Next i: Uravnen
For i = 1 To N: k3(i) = h * F(i): Next i
x = X0 + h
For i = 1 To N: Y(i) = Y0(i) + k3(i): Next i: Uravnen
For i = 1 To N: k4(i) = h * F(i): Next i
For i = 1 To N
Y(i) = Y0(i) + (k1(i) + 2 * k2(i) + 2 * k3(i) + k4(i)) / 6
Next i
End Sub
'=========================================================
14.МАТЕМАТИЧЕСКИЕ ОСНОВЫ КОНСТРУИРОВАНИЯ СИСТЕМ УПРАВЛЕНИЯ
14.1.ОБЩИЙ ПРИНЦИП МАКСИМУМА Л.С.ПОНТРЯГИНА
Общую задачу оптимального управления объектом сформулируем следующим образом. В фазо-
вом пространстве X даны две точки x
0
и x
1
: требуется из всех допустимых управлений u(t), t
0
≤t≤t
1
перево-
дящих фазовую точку из положения x
0
в положение x
1
, выбрать такое, которое придает функционалу
()
dtu,xfJ
t
t
∫
=
1
0
0
наименьшее возможное значение.
Будем полагать, что
()
0
0
>u,xf
. Введем в рассмотрение новое
63
«машинное» время, связанное с
реальным временем дифференциальной зависимостью
63
Вспомните моделирование на АВМ и применяемое там «машинное» время
126
()
dtu,xfd
0
=τ
.
В новом времени целевой функционал принимает вид
∫
τ
τ
τ−τ=τ=
1
0
01
dJ
,
т.е. задача превращается в задачу об оптимальном быстродействии. Функция
τ
(t) является непре-
рывной и монотонно возрастающей и поэтому существует обратная к ней функция t(
τ
). Имеем
() () ()
(
)
;tJt,tt,Jt,t
1010
0 0
=
==τ=τ
кроме того
()
() ()()
()
()()()()()
ττ
=
τ
τ
=
τ
tu,txf
d
dt
,tu,txf
dt
td
0
0
1
.
Определим
() ()( ) () ()()
.J,txy,tuv
≤
τ
≤
τ=ττ=τ 0
Далее пишем
() ()() ()()()
()()()()()
()()()()()
() ()()
() ()()
.
v,yf
v,yf
tu,txf
tu,txf
d
dt
dt
tdx
d
tdx
d
dy
i
i
iii
ττ
ττ
=
ττ
ττ=
=
τ
τ
⋅
τ
=
τ
τ
=
τ
τ
00
1
Таким образом, y(τ) есть решение системы
()
()
.n,...,,i,
v,yf
v,yf
d
dy
ii
21
0
==
τ
Образуем для последней системы функцию
()
()
()
0
1
,
v,yf
v,yf
v,y,H
i
n
i
i
∑
=
ϕ=ϕ
и систему для определения вспомогательных переменных
()
()
()
() ()
()
()
()
()
()
()
.
y
v,yf
v,y,H
y
v,yf
v,yf
y
v,yf
v,yf
v,yf
y
v,yf
v,yf
v,yf
v,yf
yy
H
dt
d
i
n
j
i
j
j
n
j
i
j
i
j
j
n
j
j
i
j
i
i
∂
∂
ϕ−
∂
∂
ϕ−=
=
∂
∂
⋅−
∂
∂
ϕ−=
=
∂
∂
ϕ−=
∂
∂
−=
ϕ
∑
∑
∑
=
=
=
0
1
0
1
0
00
1
0
1
1
Положим, что
() ()()
() () ()()
.v,y,H
,n,...,,i,tt
ii
τττϕ−=ψ
=
τϕ=ψ
0
21
127
() ()() ()()
(
)
()()()()()
()()
()()()()()
()() ()()()()()
()()()()()
() ()()
.tu,txf
y
tv,tyf
tv,ty,tH
y
tv,tyf
t
tv,tyf
dt
td
d
td
dt
td
dt
td
i
n
j
i
j
j
iii
0
0
1
0
1
⋅
∂
ττ∂
τττϕ−
−
∂
ττ∂
τϕ
ττ
−=
=
τ
⋅
τ
τϕ
=
τϕ
=
ψ
∑
=
Так как
()()
ttt =τ
, то
()()
(
)
(
)
(
)
(
)
txttxty
=
τ
=τ
и
(
)
(
)
(
)
(
)
(
)()
tuttutv
=
τ
=
τ
и последние соотно-
шения можно переписать
()
()
() ()()
(
)
(
)
(
)
.
x
tu,txf
x
tu,txf
t
dt
td
n
j
ii
j
j
i
∑
=
∂
∂
ψ−
∂
∂
ψ−=
ψ
1
0
0
Введем в рассмотрение вектор
(
)
(
)
ψ
ψ
=
ψ
ψ
ψ
=
,,...,,
n 010
ψ
и функцию
() ()
∑
=
ψ=ψ
n
i
i
i
u,xfu,x,H
0
в которой функции
()
(
)
t,...,t
n
ψ
ψ
1
удовлетворяют системе уравнений
()
() ()()
,n,...,,i,
x
tu,tx,H
dt
td
i
i
21 =
∂
∂
−=
ψ
ψ
(С)
а соотношения максимума записываются в виде
() ()()()
(
)
(
)()
0
≡
=
∈
tu,tx,tHu,tx,tHmax
Uu
ψψ
. (D)
Таким образом, сформулирована следующая теорема. Пусть
(
)
10
ttt,tu ≤≤
- допустимое
управление, переводящее объект из начального состояния x
0
в состояние x
1
. Если процесс
() ()()
10
ttt,tx,tu ≤≤
является оптимальным, то существует такое нетривиальное решение
() () ()()
t,...,tt
n
ψ
ψ
=
ψ
1
системы (С) и такая константа ψ
0
≤0, что для любого момента времени выполне-
но условие
максимума (D)
14.2.ОБЩИЙ ПРИНЦИП МАКСИМУМА Л.С.ПОНТРЯГИНА. ОБЩАЯ ЗАДАЧА УПРАВЛЕНИЯ
СОСТОЯНИЕМ АСИНХРОННОГО ЭЛЕКТРОДВИГАТЕЛЯ
Состояние асинхронного электродвигателя будем описывать системой
дифференциальных связей, определяющих характер изменения фазовых координат с выделением в них
управлений: относительного значения частоты и составляющих напряжения по осям координатной сис-
темы u, v -α, U
su
, U
sv
:
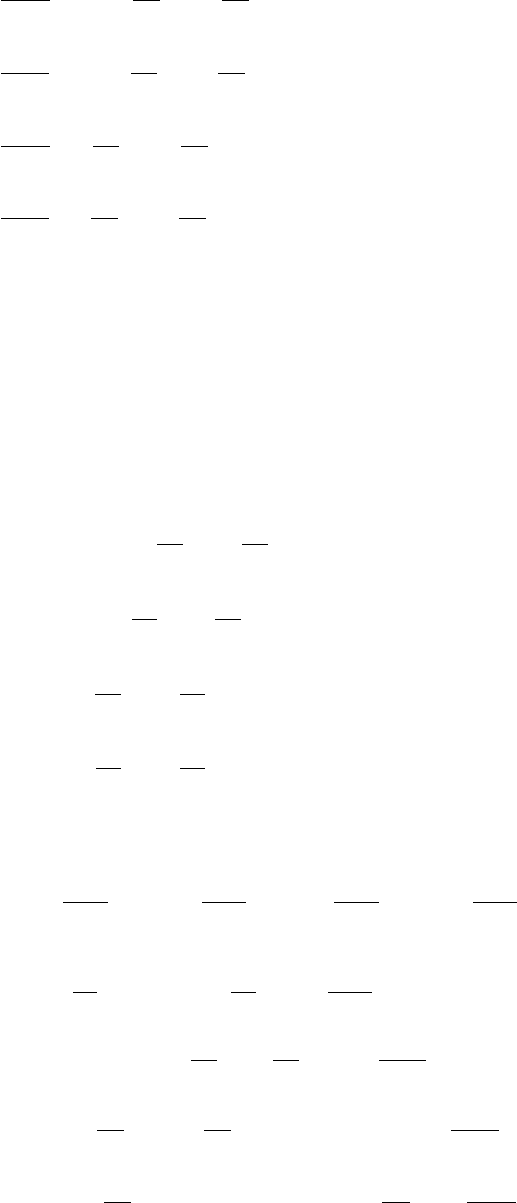
128
()
()
Ψω−αω−Ψ
′
+Ψ
′
−=
Ψ
Ψω−αω+Ψ
′
+Ψ
′
−=
Ψ
Ψαω−Ψ
′
+Ψ
′
−=
Ψ
Ψαω+Ψ
′
+Ψ
′
−=
Ψ
.pk
L
R
L
R
dt
d
,pk
L
R
L
R
dt
d
,k
L
R
L
R
U
dt
d
,k
L
R
L
R
U
dt
d
runsvs
r
r
rv
r
r
rv
rvnsus
r
r
ru
r
r
ru
sunrvr
s
s
sv
s
s
sv
sv
svnrur
s
s
su
s
s
su
su
Сформулируем задачу частотного управления АД как задачу минимизации некоторого функцио-
нала, записанного в интегральной форме и выражающего цель управления:
()
0
0
,dt,,,,fJ
t
psrs
∫
αα= UΨΨ
Условие введения управления со стороны статора требует или наличия в подынтегральной функ-
ции f
0
информации о состоянии статора, или присутствия управлений, или того и другого вместе. В про-
тивном случае следует ожидать аналитической неразрешимости задачи.
Образуем вспомогательную функцию:
()
()
() ()
()
()
()
.,,U,,f
pk
L
R
L
R
t
pk
L
R
L
R
t
k
L
R
L
R
Ut
k
L
R
L
R
UtH
psrs
runsvs
r
r
rv
r
r
rvnsus
r
r
ru
r
r
sunrvr
s
s
sv
s
s
sv
svnrur
s
s
su
s
s
su
ααΨΨψ+
+
Ψω−αω−Ψ
′
+Ψ
′
−ψ+
+
Ψω−αω+Ψ
′
+Ψ
′
−ψ+
+
Ψαω−Ψ
′
+Ψ
′
−ψ+
+
Ψαω+Ψ
′
+Ψ
′
−ψ=
0
0
4
3
2
1
и систему для определения составляющих функции ψ:
.
H
,
H
,
H
,
H
rvrusvsu
Ψ∂
∂
−=ψ
Ψ∂
∂
−=ψ
Ψ∂
∂
−=ψ
Ψ∂
∂
−=ψ
4321
&&&&
Раскрывая эти связи, будем иметь:
,
f
k
L
R
L
R
su
s
r
r
n
s
s
Ψ∂
∂
ψ−
′
ψ−αωψ+
′
ψ=ψ
0
03211
&
,
f
k
L
R
L
R
sv
s
r
r
s
s
n
Ψ∂
∂
ψ−
′
ψ−
′
ψ+αωψ−=ψ
0
04212
&
()
,
f
p
L
R
k
L
R
ru
n
r
r
r
s
s
Ψ∂
∂
ψ−ω−αωψ+
′
ψ+
′
ψ−=ψ
0
04313
&
()
,
f
L
R
pk
L
R
rvr
r
nr
s
s
Ψ∂
∂
ψ−
′
ψ+ω−αωψ−
′
ψ−=ψ
0
04324
&
Учитывая, что в условиях оптимальности
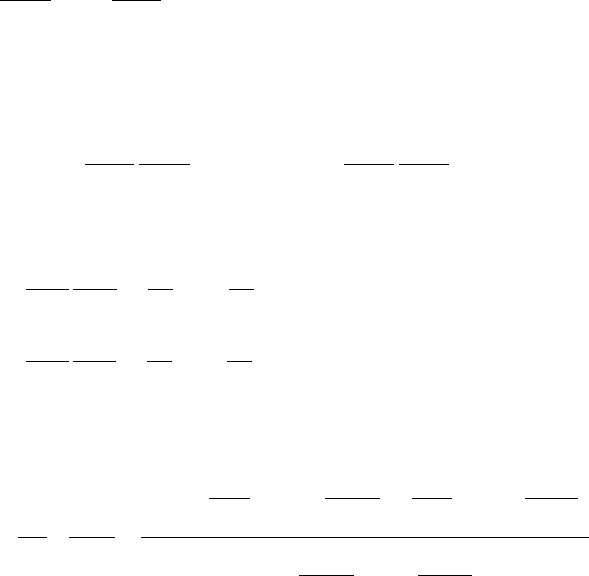
129
() () ()()()
(
)()
u,tx,tHmaxtu,tx,tH
Uu
ψ=ψ
∈
,
можем дополнительно записать, полагая непрерывность функций управления U
su
, U
sv
0 0 =
∂
∂
=
∂
∂
svsu
U
H
,
U
H
,
откуда следует:
., 0 0
21
=ψ=ψ
С учетом последнего находим:
,
f
kR
L
susr
r
Ψ∂
∂
′
ψ−=ψ
0
03
.
f
kR
L
svsr
r
Ψ∂
∂
′
ψ−=ψ
0
04
Используя выражения для составляющих вспомогательной функции ψ
в H и учитывая, что в ус-
ловиях оптимума H≡0, пишем:
()
()
()
.,,U,,f
pk
L
R
L
R
f
kR
L
pk
L
R
L
R
f
kR
L
psrs
runsvs
r
r
rv
r
r
svsr
r
rvnsus
r
r
ru
r
r
susr
r
0
0
0
0
0
0
0
=ααΨΨψ+
+
Ψω−αω−Ψ
′
+Ψ
′
−
Ψ∂
∂
′
ψ−
−
Ψω−αω+Ψ
′
+Ψ
′
−
Ψ∂
∂
′
ψ−
откуда следует
.
sv
f
ru
su
f
rv
sv
f
sv
k
s
rv
su
f
su
k
s
ru
f
k
L
R
p
s
rn
r
n
Ψ
∂
∂
Ψ
−
Ψ
∂
∂
Ψ
Ψ
∂
∂
Ψ
−
Ψ
+
Ψ
∂
∂
Ψ
−
Ψ
+
′
ω
+
ω
ω
=α
00
00
0
Таким образом, последнее выражение представляет собой требуемый конечный результат, опре-
деляющий связь частоты тока статора, параметров двигателя и цели управления, выражающейся в мини-
мизации функционала
()
0
0
.dt,,,,fJ
t
psrs
∫
αα= UΨΨ
Относительно напряжения можно сделать следующие заключения. Единственной возможно-
стью для U
su
, U
sv
отвечать требованиям, предъявляемым к вспомогательной функции H, является их мак-
симизация, т.е. для напряжения имеем
)
U(
sv
sup
U
sv
,
)
U
su
sup(
U
su
A
U
AU
=
=
∈∀
∈∀
.
Таким образом, независимо от вида критерия оптимизации, напряжение на АД следует сохранять
максимально возможным в соответствии с текущим значением частоты. Практически это означает рабо-
ту с максимальным магнитным потоком по условиям насыщения.
Рассмотрим вариант
()
()
−=
∫
∈γα∀
dtMMinfJ
t
t
n
A,
1
0
2
,
где M
n
, M - необходимое и текущее значения электромагнитного момента АД и M
n
- или констан-
та, или медленно изменяющаяся по технологическим условиям функция, т.е. f
0
=(M
n
-M)
2
.
Для этого случая
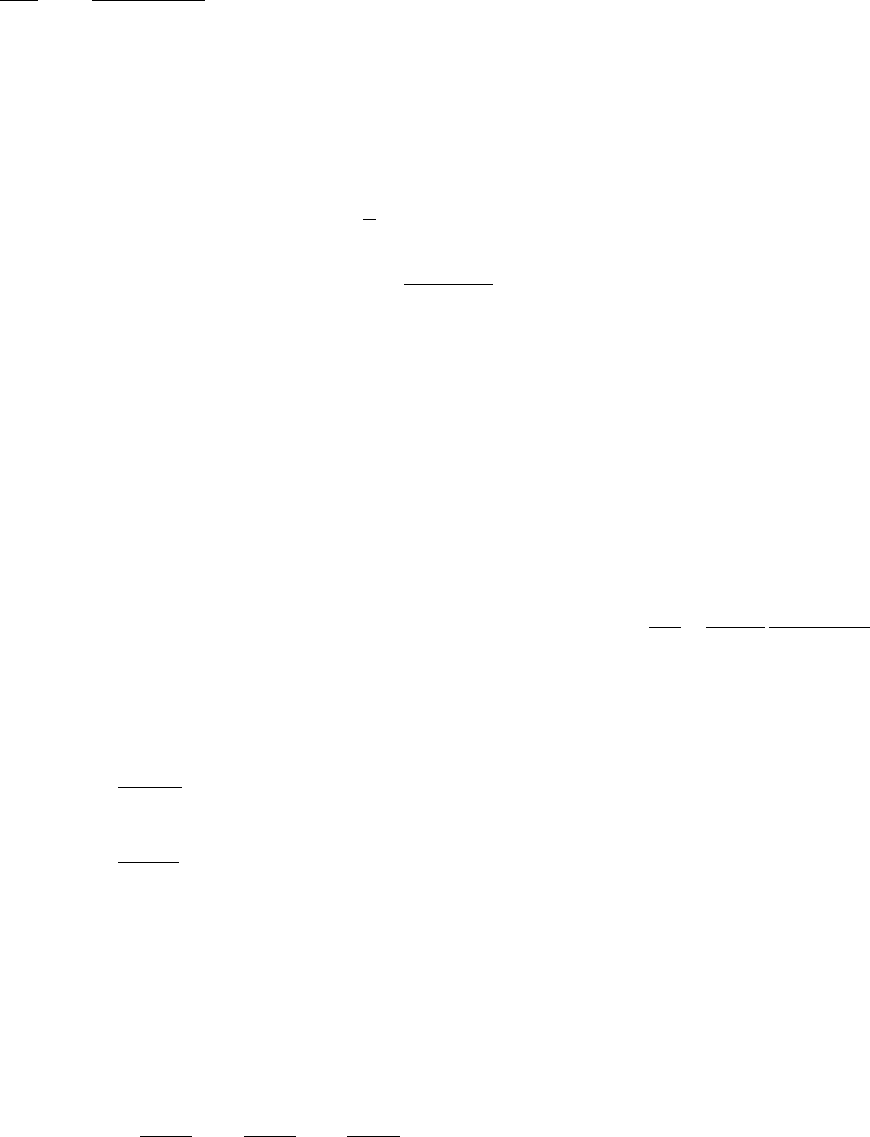
130
()
Ψ
+
+
ω
ω
=α
2
r
MM
K
p
n
n
, где
Ψ
+
Ψ
=
Ψ
222
r
v
ru
r
.
Значения электромагнитного момента и потокосцепления ротора определяются из следующих
соотношений:
()
−
+=
×=
−=
∫
,
L
L
LL
,M
,dtR
m
sss
rsmr
ss
t
t
ssss
iΨ
iΨ
iΨ
iUΨ
2
3
0
где
U
s
, - вектор напряжений питания статорной обмотки;
i
s
- вектор тока статора;
ΨΨ
r
,
s
- векторы по-
токосцеплений статора и ротора;
L
r
,
L
s
- полные индуктивности статора и ротора; L
m
- индуктивность
цепи намагничивания.
15.МАТЕМАТИЧЕСКИЕ ОСНОВЫ КОНСТРУИРОВАНИЯ СИСТЕМ УПРАВЛЕНИЯ
15.1.ПОСТРОЕНИЕ НАБЛЮДАЮЩИХ УСТРОЙСТВ
Необходимость определения значений электромагнитного момента и потока ротора при реализа-
ции аналитической конструкции оптимального управляющего устройства
(
)
Ψ
+
ω
+
ω
ω
=α
2
3
r
M
M
p
Rrp
n
nn
требует предварительного определения потокосцеплений статора.
Для отыскания значений ψ
s
α
, ψ
s
β
в различные моменты времени t воспользуемся дифференци-
альными связями
,
i
s
R
s
U
s
dt
s
d
,
i
s
R
s
U
s
dt
s
d
β
−
β
=
Ψ
β
α
−
α
=
Ψ
α
с начальными условиями ψ
s
α
=0, ψ
s
β
=0 при t=0.
Так как правые части уравнений по условиям физической реализации системы измерения опре-
деляются лишь дискретными значениями напряжений U
s
и токов статора i
s
в дискретные моменты вре-
мени t=k
∆
t (k=0,1,...,
∆
t- шаг дискредитации), то необходимо воспользоваться конечноразностной ап-
проксимацией необходимого порядка.
Воспользуемся четырех точечной схемой с узлами t
k
=t
0
+k
∆
t. Используем разложения функций и
производных в ряд Тэйлора в окрестностях ∆t, 2(∆t), 3(∆t) точки t
k
, ограничившись производными по
времени 4-го порядка
() ()
(
)
0
4
0
3
0
2
00
432
1
f
!
t
f
!
t
f
!
t
ftf
f
′′′′
∆
+
′′′
∆
+
′′
∆
+
′
⋅∆+≈
.
