Фастовец Н.О.,Тюлина А.К. Дифференциальные уравнения

21

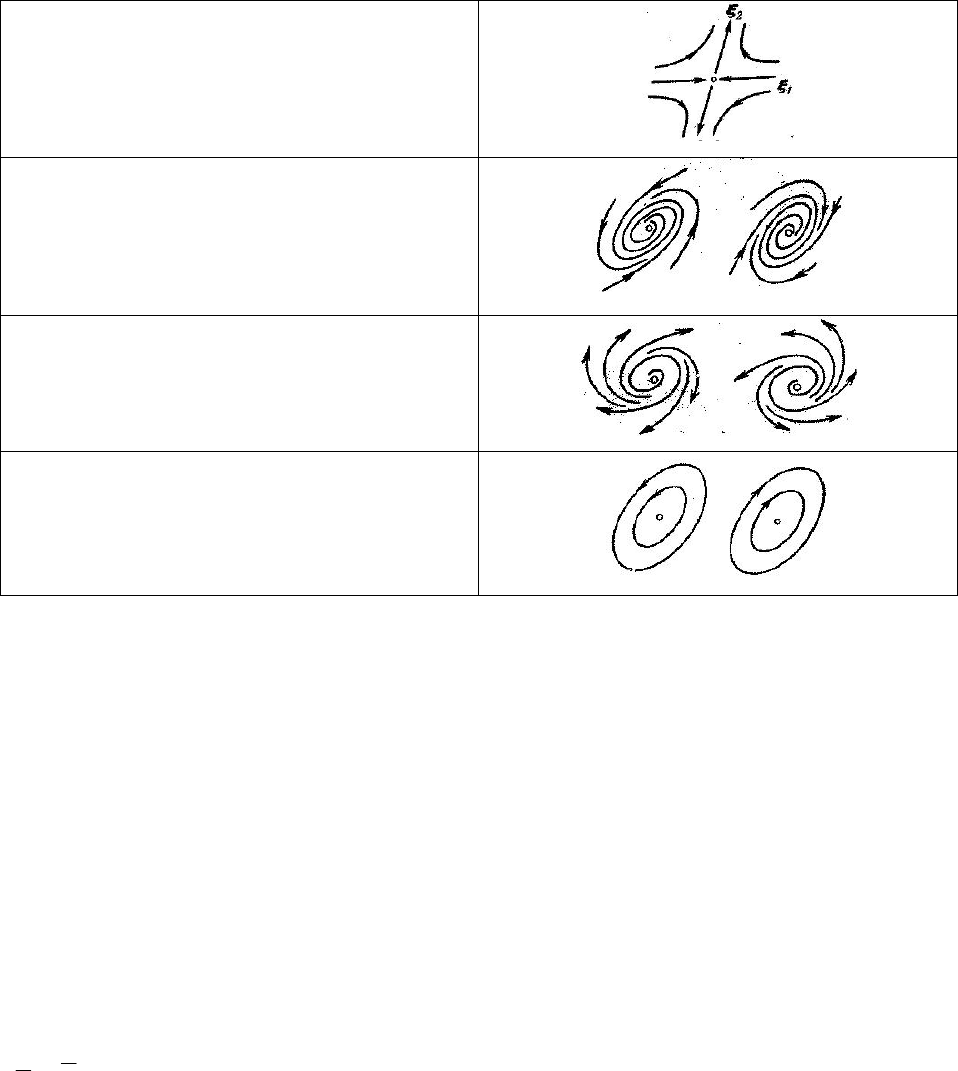
3. седло:

121 2

, 0, 0

λ

λλ λ

≠<>

4. устойчивый фокус:

1,2

, 0, 0i

λ

αβα β

=± < ≠

5. неустойчивый фокус:

1,2

, 0, 0i

λ

αβα β

=± > ≠

6. центр:

1, 2

, 0i

λ

ββ

=

±≠

2º

. Исследовать на устойчивость точки покоя следующих систем:

2.1.

11 2

212

4

32

xx x

x

xx

=−

⎧

⎨

=− +

⎩

&

;

2.2.

11 2

212

3

65

xx x

x

xx

=+

⎧

⎨

=− −

⎩

&

;

2.3.

11

212

2

xx

x

xx

=

⎧

⎨

=−

⎩

&

.

3º.

Нарисовать схематически расположение траекторий вблизи точки покоя

0

x

= в базисе из собственных векторов для задач из п. 2.

22

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Занятие 7

1º.

Комплексные числа и действия над ними.

Множеством комплексных чисел называют расширение множества веще-

ственных чисел, полученное добавлением к ним объекта, называемого мни-

мой единицей и равного по определению

1

−

. Это число обозначается i.

Таким образом, любое комплексное число имеет вид

zxi

y

=+ , где x и y -

произвольные действительные числа. Такая запись комплексного числа на-

зывается

алгебраической. Число x называется действительной частью

комплексного числа z и обозначается Re z , число y называется мнимой

частью комплексного числа z и обозначается Im z . Число

zxi

y

=+ на-

зывается комплексно-сопряженным числу z . Очевидно,

22

zz x

y

⋅= + .

Пусть даны два комплексных числа

11 1

zxiy

=

+ и

22 2

zxiy=+.

1) Два комплексных числа

1

z и

2

z равны

1212

,

x

xyy

⇔

==.

2) Сумма

1

z и

2

z определяется:

12 12 12

()( )zz xx iyy

+

=++ +.

3) Произведение

1

z и

2

z определяется:

12 12 12 12 21

()()zz xx yy ixy x y

=

−+ +.

4) Для определения операции деления надо уметь определять для любого

0z ≠ обратное число

1

z

−

≡

. Из определения сопряженного числа z вид-

но, что

1

22 22

1

x

i

y

zz

xy

x

y

−

==

++

.

Множеству комплексных чисел ставится в соответствие множество то-

чек плоскости, называемой комплексной плоскостью, по закону

(, )

x

i

y

x

y

+

⇔ .

В соответствии с полярной системой координат на этой плоскости ком-

плексное число z можно записать в виде:

(cos sin )zr

ϕ

=

+ , называемом

тригонометрической формой комплексного числа. Очевидно,

23

Re cos , Im sinxzr yzr

ϕ

== == . Величину

22

rx

y

=+ называют мо-

дулем комплексного числа z и обозначают

z , а (,]

ϕ

ππ

∈− называют

главным значением аргумента и обозначают

arg z . Одному и тому же z

соответствует бесчисленное множество значений

arg 2 , znn

ϕ

π

=+ ∈Z

.

Это множество обозначается Arg z .

2º.Основные элементарные функции комплексного перемен-

ного.

Элементарные функции комплексного переменного определяются следую-

щим образом:

(cos sin );

zx

ee xi

y

=+

cos ; sin .

22

iz iz iz iz

ee ee

zz

i

−

+−

==

Пользуясь определением функции

z

е , любое комплексное число можно за-

писать в

показательной форме:

, , arg .

i

zre r z z

ϕ

===

Для получения

всех значений обратных функций (таких, как корень п-й

степени и логарифм) необходимо пользоваться в показательной или три-

гонометрической форме φ = Arg

z .

Так, логарифмом комплексного числа z (обозначается Ln z ) называется

такое число w , что

w

ez

=

. Легко убедиться, что

Ln ln Arg ln (arg 2 ),zzizzizn

π

=+ =+ + то есть каждому числу (кроме

нуля) соответствует бесчисленное множество значений логарифма (мно-

гозначная функция), а при n = 0 значение логарифма называется

главным:

ln ln argzziz=+ .

Возведение комплексного числа в комплексную степень определяется так:

221

Ln

1

zzz

ze= .

24

3º.

Построить множества точек комплексной области:

3 3; 3 ; 1 5; 2 Im 3;

Re 2; arg ; 2 .

46

zi zi z z

zzzizia

ππ

+≤ <+<+∞ −> −≤ ≤

<−≤≤ ++−≤

Решение. Рассмотрим, например, множество 3 zi<+<+∞. Геомет-

рический смысл выражения

22

00 0

()( )zz xx yy−≡ − +−

– расстояние от

точки, соответствующей z , до точки, соответствующей

0

z . Поэтому указан-

ное множество является множеством всех точек плоскости, удаленных от

0

zi=− , то есть точки с координатами (0,–1) , более, чем на 3. Это – внеш-

ность замкнутого круга радиуса 3 с центром в (0,–1) .

4º.

Найти действительную и мнимую части следующих функций:

2

1

() 2; () 3 ; () ; () .

zi iz

fz iz z fz i z iz fz fz

zi z

−

+

=+ =++ = =

+

Решение. Рассмотрим, например, ()

zi

fz

zi

−

=

+

. Имеем

22

(1) (1) 2(1)(1)

(1) (1)

(1)

zi xiyi xiy xiy x iy y

z i xiyi xiy xiy

xy

−+−+−+− +−−−

== ⋅ = =

+−+−−+−

+−

22

2222

(1) 2(1)

(1) (1)

xy xy

i

xy xy

−− −

=+

+− +−

.

5º.

Выделить действительную и мнимую части следующих функций:

2

1

1()

; ; sin( ); ( 2) ;

zzi

z

we we w zi w

+−

== =−=−

23zi

we

−

= .

Решение. Рассмотрим, например, функцию

11

Ln( 2)

2

zz

e

−⋅

≡ . Найдем

Ln( 2) ln 2 Arg( 2) ln 2 ( 2 ), iinn

ππ

−= −+ −= + + ∈Z

.

. Сначала выделим дей-

ствительную и мнимую часть аргумента экспоненты

22

1

exp(ln2 ( 2 ) exp(ln2 ( 2 )

xiy

in in

xiy

xy

ππ ππ

⎛⎞

−

++ ⋅ = ++ =

⎜⎟

+

⎝⎠

25

22 22

(ln 2) ( 2 ) ( 2 ) (ln 2)

exp

xy

nnx

y

i

xy xy

ππ ππ

⎛⎞

++ + −

=+

⎜⎟

++

⎝⎠

. По определению экспо-

ненты:

(cos sin )

uiv u

eeviv

+

=+ получим, что действительная и мнимая

часть функции w соответственно равны:

cos

u

ev и sin

u

ev, где в нашем

случае

22 22

(ln 2) ( 2 ) ( 2 ) (ln 2)

,

x

yn nxy

uv

xy xy

π

πππ

++ + −

==

++

.

6º.

Вычислить значения функций в указанных точках:

2

cos ln 2 ; sh 1 ; ch ( ln 3); Ln( 1); ln ; sin .

22

iii ii

ππ

π

⎛⎞⎛⎞

++ −

⎜⎟⎜⎟

⎝⎠⎝⎠

7º.

Найти все значения степеней:

1

33

3

3 , ( 1) , , (1 ) .

22

i

ii i

i

+

−

⎛⎞

−+−

⎜⎟

⎝⎠

Занятие 8

ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

1º.

Пусть (, )ux

y

и (, )vx

y

– две действительные функции, определенные

в некоторой окрестности точки

00

(, )

x

y и дифференцируемые в этой

точке. Если

00 00 00 00

(,) (,), (,) (,)

xyy x

uxy vxy uxy vxy

′

′′ ′

==−

, то говорят,

что функции

(, )ux

y

и (, )vx

y

удовлетворяют условиям Коши-Римана в

точке

00

(, )

x

y .

Если функцию комплексного переменного

(), ,

f

zzxi

y

=

+ рассматривать,

как отображение плоскости ( x , y ) в плоскость ( u , v ) , где

(, ) Re (), (, ) Im ()ux

yf

zvx

yf

z==, задаваемое парой действительных

функций

(, ), (, )uuxy vvxy==

, то для дифференцируемости функции

()

f

z в точке

00 0

zxiy=+ необходимо и достаточно, чтобы это ото-

26

бражение было дифференцируемо в точке

00

(, )

x

y , и в этой точке выпол-

нялись условия Коши-Римана.

Функция

()

f

z называется аналитической в области D, если она диффе-

ренцируема в каждой точке области D.

Функция u(x,y) называется

гармонической, если

22

0

uu

xy

∂∂

+

=

∂∂

.

2º.

Пользуясь условиями Коши-Римана, выяснить, какие из следующих

функций являются аналитическими, и найти производные этих функций:

2

; ; Re ; sin3 .

z

wzz wze w z z w zi=== =−

3º.

Проверить гармоничность следующих функций:

2

22 2

22

1

2 ; ; ; ; 2 sin .

2

x

xx

ux x

y

uvx

y

v

y

ue

y

xy

+

=+− = = = =

+

4º.

Найти аналитические функции по их действительной или мнимой час-

ти, используя функции из п. 2º.

Решение. Рассмотрим способ решения такой задачи на примере

32

(, ) 3uxy x xy=−

. Найдем

22

33

u

xy

x

∂

=−

∂

. По первому условию Коши-

Римана

uv

xy

∂∂

=

∂∂

, так что

22

33.

v

xy

y

∂

=−

∂

Отсюда

22 23

(, ) (3 3 ) 3 ()vxy x y dy xy y x

ϕ

=− =−+

∫

. Дифференцируя

(, )vxy

по х и

используя второе условие Коши-Римана, получим

6() 6

u

xy

xx

y

ϕ

∂

′

+=−=

∂

,

откуда

() 0x

ϕ

′

=

, а значит ()

x

C

ϕ

=

. Итак,

23

(, ) 3vxy xy y C

=

−+ и, сле-

довательно,

32 23

() (, ) (, ) 3 (3 )

f

z uxy ivxy x xy i xy y C=+ =−+−+

. Если дано

дополнительное условие, например,

(0) 1f

=

, то можно найти постоянную

С :

(0) 1fiC== , отсюда Ci

=

− .

27

Ответ:

32 23

() (, ) (, ) 3 (3 1)fz uxy ivxy x xy i xy y=+ =−+−−.

5º.

При каких условиях функция

22

(, ) 2

x

y ax bxy cy

ϕ

=+ + будет гармо-

нической?

6º.

Дополнительная задача.

Показать, что в полярных координатах r и φ условия Коши-Римана

имеют вид

11

,

uvv u

rr r r

ϕ

∂∂∂ ∂

==−

∂∂∂ ∂

.

Решение. В полярных координатах

cos , sinxr yr

ϕ

=

= , а

(, ) (cos , sin )uxy ur r

ϕ

= , (, ) (cos , sin )vxy vr r

ϕ

=

. Поэтому

cos sin

uuxuyu u

rxryrx y

ϕ

∂∂∂∂∂∂ ∂

=+= +

∂∂∂∂∂∂ ∂

;

(sin) s

vvxvyv v

rrco

xyx y

ϕ

ϕϕϕ

∂

∂∂ ∂∂ ∂ ∂

=+=−+

∂∂∂∂∂∂ ∂

.

Учитывая условия Коши-Римана

,

uv vu

xy

x

y

∂

∂∂∂

=−=

∂

∂∂∂

, во второй

строчке имеем:

(sin ) s

vu u

rrco

yx

ϕ

∂∂ ∂

=+

∂∂ ∂

, так что, сравнивая это соот-

ношение с первой строчкой, получим первое из доказываемых соотношений:

1uv

rr

ϕ

∂∂

=

∂∂

. Выписав соответственно две другие частные производные

v

r

∂

и

u

ϕ

∂

, аналогично получим второе условие Коши-Римана.

Занятие 9

ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

1º.

Пусть однозначная функция () (, ) (, )

f

zux

y

iv x

y

=

+ непрерывна в об

ласти D и С - кусочно-гладкая кривая, лежащая в D . Вычисление инте-

28

грала от функции комплексного переменного сводится к вычислению кри-

волинейных интегралов по кривой С

()

CC C

f

z dz udx vd

y

ivdx ud

y

=−+ +

∫∫ ∫

.

2º. Теорема Коши (для односвязной области).

Если ()

f

z аналитическая в односвязной области D , то () 0

C

fzdz

=

∫С

, где

С – любой кусочно-гладкий замкнутый контур, лежащий в D .

Теорема Коши (для многосвязной области).

Если

()

f

z

аналитическая в области D ,

граница которой С состоит из конечного

числа замкнутых кусочно-гладких кривых и

непрерывна в замкнутой области

D

, то

() 0

C

fzdz=

∫С

.

Заметим, что в данной теореме интеграл по границе С распадается на от-

дельные контурные интегралы, и обход каждого из них ведется в таком на-

правлении, чтобы область находилась слева (показано стрелочками на ри-

сунке).

3º.

Если С задана параметрически:

[]

12

(), (), ,

x

xt y yt t t t==∈, то

2

1

() (()) ()

t

Ct

f

zdz

f

zt z tdt

′

=

∫∫

, где () () ()zt xt i

y

t

=

+ .

Если

()

f

z

аналитическая в области D , содержащей точки

1

z и

2

z , то

имеет место формула Ньютона–Лейбница

2

1

21

() ( ) ( )

z

f

zdz z z=Φ −Φ

∫

, где

()zΦ

– какая-либо первообразная для функции

()

f

z

.

3.1. Пример: Найти

(1 2 )

C

izdz+−

∫

, где

а) С – прямая, соединяющая точки

12

0 и 12zzi

=

=+ ;

29

б) С – дуга окружности 1, 0 arg

2

zz

π

=

≤≤ .

Решение. а) Имеем

1 2 (1 2 ) (1 2 )iz xi y

+

−=− ++

. Тогда

(1 2 ) (1 2 ) (1 2 ) (1 2 ) (1 2 )

CC C

i z dz x dx y dy i y dx x dy+− = − − + + + + −

∫∫ ∫

.

Уравнение прямой, соединяющей точки

12

и zz, будет

2, 0 1

y

xx=≤≤, откуда 2d

y

dx

=

. Поэтому

[][]

11

00

(1 2 ) 1 2 (1 4 ) 2 1 4 (1 2 ) 2 6 3

C

i z dz x x dx i x x dx i+− = − − + ⋅ + + + − ⋅ =−+

∫∫ ∫

.

б) если С – дуга окружности

1, 0 arg

2

zz

π

=

≤≤, положим

,

ii

ze dzied

ϕ

== . Тогда

222

000

(1 2 ) (1 2 ) (1 ) 2

ii i ii

C

i z dz i e de i de e e id

π

ππ

ϕϕ ϕ ϕϕ

ϕ

−−

+− = +− = + − =

∫∫ ∫∫

()

2

0

(1 ) 2 (1 ) 1 2 2

2

i

ie i d i i i i

π

ϕ

π

ϕ

π

=+ − =+ −− =−−

∫

.

4º.

Решить:

4.1.

z

C

edz

∫

, С – отрезок прямой, соединяющей точки

12

0 и zzi

π

==− .

4.2.

Im

C

zzdz

∫

, С :

1, arg 0zz

π

=

−≤ ≤

. Рассмотреть два способа

параметризации:

а)

, 0

i

ze

ϕ

πϕ

=−≤≤ ,

б)

cos sin , 0ztit t

π

=

+−≤≤.

4.3.

3

()

z

C

zedz+

∫

, С :

30

а) 3z = ,

б)

3, 0 arg

2

zz

π

=≤≤ .

5º. Интегральная формула Коши.

Для функции ()

f

z , аналитической в области D, и любого замкнутого кон-

тура С, лежащего в D и содержащего точку

o

z

, справедлива формула

1()

()

2

o

C

f

zdz

fz

izz

π

=

−

∫С

.

В тех же предположениях справедлива

Интегральная формула Коши для производных:

()

1

!()

()

2

()

n

o

n

C

o

nfz

f

zdz

i

zz

π

+

=

−

∫С

.

Пример: Найти

2

3

z

C

e

dz

zz

−

∫С

, если а) С : 1z

=

; б) С : 4z = .

Решение. а)

2

22

2

0

3

2

33

3

z

zz

CC

z

e

z

eei

dz dz i

zz

π

=

⎛⎞

⎜⎟

−

⎝⎠

===−

−

∫∫СС

.

б) Первый способ. Можно разложить

2

111

33(3)

3

zz

=− +

−

.

(

)

222

22

2

03

444

11 2

3333

3

zzz

zz

zzz

eeei

dz dz dz e e

zz

π

==

===

=− + = − + =

−

∫∫∫ССС

6

(1)2

3

ei

π

−

=

.

Второй способ (по теореме Коши для многосвязной области). Особые

точки подынтегральной функции

1

0z

=

и

2

3z

=

окружим окружностями

1

γ

и

2

γ

столь маленьких радиусов, что они обе лежат внутри круга 4z

<

и не

пересекаются. Согласно теории криволинейных интегралов, общая граница

области, состоящей из этого круга с вырезанными из него таким образом ма-

Фастовец Н.О.,Тюлина А.К. Дифференциальные уравнения

Подождите немного. Документ загружается.