Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

170 3 Oceans and Atmospheres

We do not offer much assessment of the likely size of Γ . We might expect γ not to

be large (otherwise there is a signiﬁcant shear layer at the troposphere), and that E

would be less than its value at the surface. In this case, Γ ≈

γE

,andmaybesmall.

We must also prescribe continuity of pressure; expanding hydrostatic tropo-

spheric and stratospheric pressures in Taylor series about z =1, and using continu-

ity of density and pressure at the tropopause, but allowing for a jump in the vertical

temperature gradient, we ﬁnd the pressure condition becomes

ψ =cη

at z =1, (3.144)

where

c =



∂

∂z



−

. (3.145)

Together, (3.142) and (3.144) give a condition on ψ at z = 1, in which W is given

from the energy equation (3.124). We need one further boundary condition for ψ at

z =0.

The quantity ψ represents both pressure (P =¯ρψ) and potential temperature

(Θ =∂ψ/∂z). We have already speciﬁed our one pressure condition, so any bound-

ary condition on ψ must come from the thermal boundary condition at the surface.

We need to be careful about this, however.

A suitable sort of boundary condition on Θ would appear to be to prescribe

Θ = Θ

S,L

, where for the sea (Θ

) we would take the saturation potential tempera-

ture derived from (2.92), and on land, Θ

(y, t) would represent the daily oscillation

about a mean temperature which varies with latitude. Latitudinal variation of aver-

age surface (and thus potential) temperature from equator to pole is about 60 K over

a distance of 10

km,

or 6 K per 10

km, a dimensionless amplitude of about

0.02 ∼ε

, consistent with a secular variation of mean Θ with latitude y.

However, the energy equation (3.124) is hyperbolic for Θ, and the loss of the

conductive terms means that the prescription of surface potential temperature has

no (short term) effect on tropospheric potential temperature beyond the plane-

tary boundary layer. For example, inclusion of an appropriate eddy diffusive term

∇

Θ leads to the conclusion that on the relevant daily time scale (note that

l/U ∼ 14 hours) a surface ﬂuctuating potential temperature only penetrates a dis-

tance of O(ε) into the troposphere.

In obtaining the quasi-geostrophic equation (3.137), we took a z derivative of

the energy equation. Therefore the undifferentiated form (3.124) provides the extra

boundary condition for Θ =∂ψ/∂z at z =0: speciﬁcally,



∂ψ

∂z



=H −SE

∗

∇

ψ on z =0. (3.146)

The distance is very close to this exact value because that is how the French Academy of Sciences

intended to deﬁne the metre in 1791.

3.5 The Quasi-geostrophic Approximation 171

To see how these conditions determine a solution (and how a numerical scheme

might be implemented), suppose that S and W are known. (3.140) and (3.144) then

give a boundary condition for ψ at z = 1; (3.146) gives a boundary condition for

∂ψ/∂z at z = 0. Together with appropriate x and y ﬂow conditions, we can solve the

potential vorticity equation for ψ. The unknowns W and S are then determined by

(3.118) with the boundary condition (3.138), and the consistency condition (3.126).

Surface Temperature and Planetary Vorticity

The energy equation (3.124) is thus applied in the boundary conditions at both z =0

and z = 1. The question arises as to what a suitable choice of initial condition for

Θ is. This question is associated with the only remaining closure of the model to

be made, which is the choice of the surface temperature scale T

. Although the

boundary ﬂuxes are small, it is they which determine the mean temperature over

long time scales.

Thus (3.25) states that the total energy I +P +M is constant

on short time scales, but over long time scales its value is determined by the ﬂuxes

on the right hand side. Thus the correct choice for T

follows from a global energy

balance, as we earlier surmised.

A more detailed consideration of energy balance considers the variation of solar

variation with latitude. If we simply time-average (but not space-average) (3.25),

then we ﬁnd a latitude-dependent surface temperature which varies slowly with y.

Taking account of angle of solar insolation, Question 3.6 suggests an appropriate

choice is

Θ ≈1 −s

y −s

at z =0, (3.147)

where s

≈1, s

≈0.14. We emphasise that it is not necessary to apply (3.147)asthe

initial condition for the potential temperature perturbation Θ, but it is a physically

sensible choice which reﬂects the long time-average surface temperature.

In a similar way, there are small horizontal diffusive terms missing from the

potential vorticity equation. Over long time scales, we might expect these to render

q in (3.139) uniform in y, even though this is not required by (3.148) (below).

3.5.2 The Day After Tomorrow

Although it is common to suppose that the stratiﬁcation parameter S is prescribed,

we have seen that in fact it is determined (for the normal case of stationary solutions)

This argument is similar to that of the Prandtl–Batchelor theorem, which says that in a steady

two-dimensional high Reynolds number ﬂow, vorticity is constant inside any closed streamline.

The argument is that u.∇ω = Re

−1

∇

ω ≈0, so that ω ≈ ω(ψ), but exact integration of the vor-

ticity equation round the closed streamline using the divergence theorem implies that ω



(ψ) ≈0,

thus ω ≈ constant. The same kind of argument yields the isothermal core of convection cells at

high Rayleigh number (see Chap. 8).

172 3 Oceans and Atmospheres

from (3.134). In stationary conditions, since



is constant, we see that the right hand

side of (3.137) vanishes, and the quasi-geostrophic equation takes the form



∇

ψ +βy +

∗



∇

¯ρ

∂

∂z



∂ψ

∂z



=0. (3.148)

The single equation (3.148) is thus a (nonlinear) integro-differential equation for

ψ, and is to be solved subject to the boundary conditions (3.142), (3.144) and

(3.146). Using (3.134), (3.124) and (3.115), the boundary conditions on surface and

tropopause can be written in the form



∂ψ

∂z





1 −

∇



∇



on z =0 (3.149)

and

√



H −

Dψ



∗



∇

¯ρH

+Γ ∇

ψ on z =1. (3.150)

It is presently observed in the atmosphere that S is positive, or equivalently that



∇

is positive (if we suppose H>0 for a near adiabatic temperature gradient),

and this is necessary for basic static stability; but it is not mathematically obvious

that the solution of (3.148) will always give a positive mean surface vorticity



;

nor is it necessary that H>0. So long as the average surface vorticity remains

positive, the weather remains ﬂuctuating but stable. There are storms, sometimes

violent, but they die away in time. In fact, mid-latitude depressions have a cyclonic

(anti-clockwise) rotation,

and thus have positive vorticity. The rôle of storms may

be thought of as a means of generating the positive vorticity necessary for well-

posedness.

There are two ways in which the quasi-geostrophic model can break down. One

is if H becomes negative. In Question 3.5, it is shown that H can be approximately

represented as

H =

(4α −1)T

+νSt aM(T , p))

, (3.151)

in which we use the adiabatic approximation that T and p are given by

T(z)=1 −αz,

p(z) =(1 −αz)

1/α

(3.152)

In the northern hemisphere: clockwise in the southern hemisphere.

There is a potentially interesting analogy with two-phase ﬂow models here; see the discussion

following Eq. (3.155).

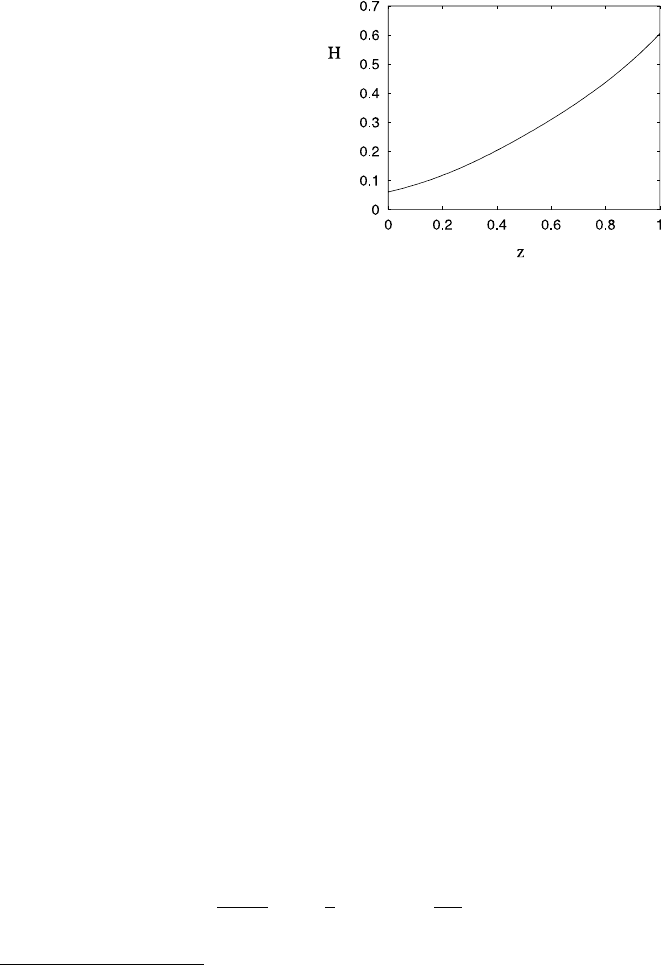
3.5 The Quasi-geostrophic Approximation 173

Fig. 3.3 H(z) computed

from (3.151)usingvalues

α = 0.29, a =18.8, St =8.7,

ν =0.01

and M(T,p) is given by (3.65). Figure 3.3 shows the variation of the dimension-

less heating according to this expression for parameters appropriate to the Earth at

present. We note that H>0, and is an increasing function. The size of the increase

is exaggerated, since it is observed that S decreases with height (a factor of two be-

tween surface and tropopause), while density decreases by a factor of about three,

and thus we would expect (given (3.134)) an increase of H of about 1.5. Obvious

quantitative reasons for the discrepancy lie in the assumptions of a grey, opaque,

saturated atmosphere. The value of H given by (3.151) is very sensitive to varia-

tions in the parameter α.Ifα is reduced from 0.29 to 0.25, then H = 0, and for

α<0.25, H<0. Variation of α is largely due to atmospheric composition. For a

atmosphere, such as we have on Venus, α = 0.19,

and then we would have

H<0.

Zonal Flow

The other way of breaking down is if



∇

< 0. In order to see whether this could

occur, it is necessary to solve the quasi-geostrophic potential vorticity equation. In

general this is a numerical task, but some insight can be gained from the considera-

tion of simple solutions. The simplest kind of ﬂow is a zonal ﬂow, in which there is

no x dependence and a purely westerly ﬂow, ψ =ψ(y,z). There is no unique such

solution, but one possibility, which satisﬁes the equations and boundary conditions

(3.148), (3.149) and (3.150), is

ψ =(1 −s

y)z −

¯ρHβ

∗





1 −



∗

¯ρΓ





, (3.153)

The molecular weight of CO

is 44.

And indeed, weather on Venus is very different, but whether this has anything to do with the

present discussion is unclear; the planetary rotation rate is extremely small, so that the Rossby

number is likely to be large, and the lower atmosphere is very dense, and thus more like an ocean.

Only the upper atmosphere is more active, and there is some evidence for lightning storms there.

174 3 Oceans and Atmospheres

where for simplicity we take H and ¯ρ to be constant. The corresponding potential

vorticity is

q =





1 −



∗

¯ρΓ





. (3.154)

This solution exists for arbitrary



, but the discussion concerning (3.147) suggests

that we prescribe Θ and thus ψ

on z =0. The choice (3.147) then determines the

mean surface vorticity as



2 ¯ρΓ s

¯ρΓ +E

∗

, (3.155)

and thus positive, which is encouraging.

Suppose for the sake of argument that a choice such as (3.155) applies even for

unsteady ﬂows. The stratiﬁcation parameter S =

¯ρH

∗



is thus positive for H>0 and

negative for H<0. For increasing CO

composition of the atmosphere (for exam-

ple), S will become negative, and the quasi-geostrophic potential vorticity equation

becomes ill-posed. What then?

In Sect. 3.6.2 below, we show that a steady zonal ﬂow becomes unstable for

sufﬁciently small (positive) S. There is an interesting analogy here concerning this

instability of a zonal ﬂow as S is reduced, and the ill-posedness which occurs if

S becomes negative. Bubbly two-phase ﬂows are thought to become unstable to

kinematic waves as the bubble volume (void) fraction increases, and this heralds

the breakdown of the bubbly ﬂow régime as the bubbles coalesce, forming a slug

ﬂow. It is also the case that appropriate two-phase ﬂow models become ill-posed as

the void fraction is increased further above the wave instability threshold. Appar-

ently, the ﬂow régime selects itself in such a way as to avoid ill-posedness in the

corresponding model.

The analogy lies in the idea that the potential vorticity equation is ill-posed if

S<0; but an instability occurs before this can happen, if S<S

for some positive

. This instability is a herald of the ill-posedness, and the consequent breakdown

of the quasi-geostrophic régime. On the Earth, this instability is already in place. It

is a herald of the breakdown of our weather systems.

We are used to the atmosphere behaving in one (quasi-geostrophic) way, but there

is little to say that alternative behaviours are not possible. We are now used to the

idea that oceanic circulation and ice sheet extent can occur in different states: ice

sheets in the last ice age surged over time scales of hundreds of years, oceanic cir-

culation switched off and on over time scales of decades. We have not countenanced

the more frightening idea that atmospheric circulation might also change rapidly.

If the mean surface vorticity becomes negative, then the surface temperature

starts to rise on the convective time scale (14 hours, with l = 1300 km, U =

26 m s

−1

), and the negative stratiﬁcation causes global storms and massive planet-

wide atmospheric overturn. The gentle, quasi-geostrophic régime is lost, and the

weather becomes relentlessy stormy. The resultant massive cloud cover causes an

abrupt increase in the greenhouse effect, with the consequent rise in temperature

giving a positive feedback effect on surface evaporation.

3.6 Rossby Waves 175

Some of these effects are graphically portrayed in the ﬁlm, The Day After To-

morrow, in which collapsing ice shelves and ocean currents magically combine to

cause a meteorological upheaval in a matter of days. One might suppose that this

is the stuff of fantasy, but it may be that a régime change on the Earth is possible,

leading to weather changes far worse than that imagined in the ﬁlm. If a transition

were imminent, then one might expect to see increasing signs of instability: worse

storms, more extreme events. This, of course, is thought by some to be exactly what

has been happening over the last several decades.

3.6 Rossby Waves

We now seek a wave motion corresponding to the zero frequency geostrophic grav-

ity wave mode satisfying (3.106) with ω = 0. This is the Rossby wave, and it is

most simply examined by studying (3.137) in the absence of heating, and assum-

ing that the stratiﬁcation parameter S is prescribed. (Such simpliﬁcations are in fact

commonly made in studying the properties of (3.137).) We deﬁne a vertical eigen-

function Ψ(z)satisfying the ordinary differential equation

¯ρ



¯ρ



=−m

Ψ, (3.156)

where for suitable homogeneous boundary conditions on Ψ , m

will be positive.

With H = 0, ψ = 0 is a solution of (3.137), and small amplitude solutions of the

equation will satisfy the linearised equation

∂

∂t



∇

ψ +

¯ρ

∂

∂z



¯ρ

∂ψ

∂z



+β

∂ψ

∂x

=0. (3.157)

This has solutions

ψ =Ψ(z)exp



i(kx +ly +ωt)



, (3.158)

providing

ω =

kβ

. (3.159)

These are Rossby waves. The wave speed −ω/k is negative, so that the waves move

westwards. The sphericity of the Earth (i.e., β>0) is essential in causing the waves

to move. If there is a constant zonal ﬂow U , then a similar analysis shows that the

wave speed is

−

=U −

, (3.160)

so that the westward drift is relative to the mean ﬂow.

176 3 Oceans and Atmospheres

3.6.1 Baroclinic Instability

Gravity waves are the sound of the atmosphere. Like a bell which reverberates when

struck, gravity waves are excited externally. For example, when the atmosphere

ﬂows over mountains, the waves are visualised by the periodic rows of clouds which

form in the lee. However, they do not play a prominent part in large scale weather

ﬂows, because they are damped fairly rapidly by friction, and they are generated by

external effects such as topographic forcing, not by internal dynamics.

Rossby waves, on the other hand, do play an important part in the day to day

weather, and this is because they are continually generated by an instability in the

underlying basic zonal ﬂow. This instability is called baroclinic instability, and it is

responsible for the basic wave-like nature of the circulation in mid-latitudes.

We consider the stability of a basic state which is taken to be a purely zonal ﬂow.

Because the quasi-geostrophic model is essentially inviscid (and conductionless),

there is no unique such state. In the absence of the heating term H on the right

hand side of (3.137), any zonal stream function ψ(y,z) satisﬁes the QG equation

(3.137). However, we would expect that over sufﬁciently long time scales, the po-

tential temperature Θ of a zonal ﬂow would become equal to the underlying surface

temperature Θ

(y), which ultimately is what drives the ﬂow. A local expansion on

the mid-latitude length scale of the global O(ε) variation in θ suggests the prescrip-

tion of Θ

=−y at z =0. The choice Θ =−y implies the zonal ﬂow

ψ =k −yz; (3.161)

generally, k =k(z) but we will take it as constant. We will use (3.161) as the basic

state whose stability we wish to study. However, we have to be careful to ensure

that the model we study is consistent with this basic state! In terms of the full quasi-

geostrophic model, (3.161) satisﬁes (3.124) and (3.118) with W = 0 from (3.138),

H =0 and S arbitrary. The conditions (3.140) and (3.144) then allow

η =



k −y



1/2

, (3.162)

where

c =



∂T

∂z



−

> 0. (3.163)

3.6.2 The Eady Model

The simplest model in which baroclinic instability is manifested is the Eady model.

In this model, the tropopause is considered to be a rigid lid, so that we impose

W =0atz =1. (3.164)

3.6 Rossby Waves 177

This follows from (3.140) and (3.144) in the limit that c →∞. Basal friction is

ignored, corresponding to E

∗

→0in(3.138), so that

W =0atz =0. (3.165)

The Earth’s sphericity is ignored by putting β =0, we take the heating term H =0

(consistent with the basic state (3.161)), and both the density ¯ρ and the stratiﬁcation

S are taken as constant. The equation to be solved is thus the QG equation in the

form



∇

ψ +

∂

∂z



=0, (3.166)

with boundary conditions which derive from (3.124):



∂ψ

∂z



=0atz =0, 1, (3.167)

together with the no ﬂow conditions ∂ψ/∂x = 0ony =±1. In addition, (3.118)

implies that



ζdz=0. (3.168)

This is automatically satisﬁed when ψ satisﬁes (3.166) and (3.167).

We write (taking k =1 without loss of generality)

ψ =1 −yz +Ψ, (3.169)

and linearise for small Ψ to ﬁnd



∂

∂t

∂

∂x



∇

Ψ +

∂

∂z



=0, (3.170)

subject to



∂

∂t

∂

∂x



∂Ψ

∂z

−

∂Ψ

∂x

=0onz =0, 1,

Ψ =0ony =±1.

(3.171)

We seek solutions as linear combinations of the form

Ψ =A(z)e

σt+ikx+il

, (3.172)

where l

= nπ/2, and n is an integer. The appropriate linear combination of the

y-dependent part is sin l

y for n even, and cos l

y for n odd. Then

(ikz +σ)





−μ



=0, (3.173)

178 3 Oceans and Atmospheres

Fig. 3.4 Wave speed of

perturbations in the Eady

model. Instability occurs

where the wave speeds are

complex conjugates, for

μ  2.4

where





S, (3.174)

and

(ikz +σ)A



−ikA =0onz =0, 1. (3.175)

Smooth solutions of (3.173) are linear combinations of cosh μz and sinh μz, and

the dispersion relation which results from satisfaction of the boundary conditions in

(3.173)is

c =−



−coth



−tanh



1/2

, (3.176)

where c is the wave speed. Figure 3.4 shows the (real) value of c as a function of

(positive) μ. Since μ/2 > tanh(μ/2), it is clear that c is complex for μ<μ

, where

=coth

,μ

≈2.399. (3.177)

Complex conjugate values of c indicate instability, and this occurs for μ<μ

Instability occurs if k

+ l

<μ

/S, and thus is effected by the minimum values

k =0, l =π/2, and the Eady instability criterion is

4μ

≈2.218; (3.178)

this is readily satisﬁed in the Earth’s atmosphere.

Evidently, the waves (stable or unstable) move to the east in the northern hemi-

sphere, as is observed. The wave speed of unstable waves is 0.5, and the growth rate



coth

−



−tanh



1/2

. (3.179)

The growth rate goes to zero as k → 0, and also as μ → μ

. Since for the funda-

mental mode n =1, μ

=(k

)S increases with k, the growth rate is maximum

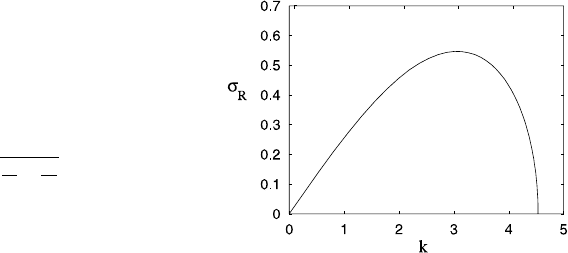
3.7 Frontogenesis 179

Fig. 3.5 Growth rate σ

perturbations in the Eady

model as a function of wave

number k when the

stratiﬁcation S =0.25. The

growth rate is well

approximated by

≈0.145k(k

−k)

1/2

where k



−

is the

maximum wave number for

instability

for an intermediate value of k. Indeed, Fig. 3.5 shows a typical graph of the growth

rate plotted as a function of wave number k. Although linear stability gives us no

information about the eventual form of the growing waves, it is plausible that the

maximum growth rate at wave number k

selects the preferred wavelength of dis-

turbances as 2π/k

. This appears to be consistent with actual synoptic scale waves

in mid-latitudes.

3.7 Frontogenesis

What has all this to do with the weather? If we look at a weather map, or listen to a

weather forecaster on a mid-latitude television station, we will hear about fronts and

depressions, low pressure systems, cyclones and anti-cyclones. These are indeed the

standard bearers of the atmosphere, bringing their associated good and bad weather,

storms, rainfall and snow. We are now in a position at least to describe how these

features occur.

The weather is described, at least in essence, by some form of the geostrophic

or quasi-geostrophic equations. Dissipative effects due to eddy viscosity and eddy

thermal conductivity have a short term (days) effect in the planetary boundary layer

within a kilometre or so of the surface, but only control the mean temperature of the

troposphere over much longer time scales. As a consequence, weather is effectively

described by a conservative system, indeed certain approximate models can be writ-

ten as a Hamiltonian system, and as a consequence it is subject to the same sort of

large amplitude ﬂuctuations as those which characterise instability in such systems.

The basic poleward gradient of surface temperature attempts to drive a zonal

ﬂow, which is linearly unstable in the presence of a sufﬁciently small stratiﬁcation

parameter S. The very simplest representation of this instability is found in the Eady

model (3.166) and (3.167), which is a nonlinear hyperbolic equation for the potential

vorticity q. The consequence of the instability is that the steady, parallel character-

istics of the zonal ﬂow are distorted and intersect, forming a shock, as illustrated in

Fig. 3.6. This is a front. It consists of a tongue of cold air intruded under warmer air,

and the width of the front is typically of order 100 km.