Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

200 3 Oceans and Atmospheres

six hours). At the poles the tides are in phase. In-phase tides are called direct, and

out-of-phase tides are called indirect. At a latitude of cos

−1

(1/S) ≈65

◦

, resonance

occurs and tides can be signiﬁcantly higher than the peak equilibrium tide of about

0.4 m.

Ocean Basins

In reality, there are continents, and these act as boundaries to the oceanic tidal ﬂow.

The free canal tidal wave given by (3.278) is a particular solution of the forced wave

equation (3.271), but in an ocean basin, or in a canal with ends, free waves of the

system are excited in order to prevent overﬂow at the ends. A solution for the case

of a narrow canal at latitude λ with ends at longitude φ =±

is easily found with

the same method as above, except that we allow the solution to depend on t and φ

independently. We ﬁnd η =χ +f(φ,t), and the integrability condition for f takes

the form

cos

λf

−f

φφ

=4S

cos

λχ, (3.279)

and solving this subject to f

= 0atφ =±

, we ﬁnally obtain the solution (see

also Question 3.11)

η =

cos

δ cos

1 −S

cos

[A cos 2St +B sin 2St], (3.280)

where

A =cos2φ −

S cos λ sin L cos(2Sφ cos λ)

sin(LS cos λ)

B =−sin 2φ +

S cos λ cos L sin(2Sφ cos λ)

cos(LS cos λ)

(3.281)

The ﬁrst terms in the expressions for A and B represent the forced tidal wave, and

the second terms represent the free oscillations in the basin at the same frequency.

We see that resonance occurs if S cos λ =1, as before, or if

2LS cos λ =nπ, (3.282)

for integral n.

3.11.3 Seiches

A particular example of the tidal oscillations which occur in closed basins is af-

forded by the waves observed in lakes, termed seiches. For these, rotational effects

are indeed small, and the relevant value of L is also. In addition, the depth of lakes

is much less than that of the ocean, so that the tidal forcing coefﬁcient S is larger.

3.11 Tides and Tsunamis 201

For example, for a lake of length 80 km and depth 100 m, we have L ∼ 0.02 and

S ∼15. Supposing the lake to be narrow and aligned with φ, we write

φ =φ

, (3.283)

and then (3.281) is approximately (for L 1)

A =cos2φ −

Λ cos 2Λξ

sin Λ

B =−sin 2φ +



Λ sin 2Λξ

cosΛ



(3.284)

where

Λ =LS cos λ. (3.285)

The dominant coefﬁcient is B, since Λ can be a good deal larger than L. With the

lake dimensions above, at λ =

, Λ ≈0.2. After some algebra and approximation,

we ﬁnd the tide given by (3.280) to be approximately

η ≈

cos

sin 2Λξ sin 2St, (3.286)

giving a standing wave of fairly small amplitude. The decrease of depth at the lake

margins can enhance the amplitude considerably.

3.11.4 Amphidromic Points

The solution above in (3.280) for a canal represents the superposition of the forced

westward travelling wave with two waves (bound by the basin) having the natural

speed of the oceans (which is one, in these dimensionless units). When resonance

occurs, this canal solution takes on the form of a standing wave.

Suppose, for example, that

LS cos λ ≈

; (3.287)

then the dominant part of the solution in (3.280) can be written as

η ≈−



π cos L

L(2LS cos λ −π)



sin

πφ

sin 2St, (3.288)

and is a standing wave; in particular, there is a nodal point at φ = 0 where η ≈ 0:

at that point there is approximately no tide. If we consider the dominant part of the

202 3 Oceans and Atmospheres

coefﬁcient A in (3.281), then we ﬁnd that it is generally non-zero at the resonant

canal length; however, if we choose

2L ≈π sin L (3.289)

as well as (3.282), then there is a genuine nodal point.

In our discussion so far, we have neglected Coriolis force and the sphericity of

the Earth. It is really not sensible to do this, since tidal forcing gives fundamentally

two-dimensional motion, but the simpler analysis does illuminate two ideas, which

turn out to be central in understanding how the tides work. The ﬁrst is the idea of the

tide as a wave, and the second is the idea that there can be nodal points. These two

features essentially describe the real tide. The nodal points where the tidal amplitude

vanishes are called amphidromic points.

We go back to the linearised model (3.269), again taking h =1. It is clear that

tidally forced solutions will be periodic, and we therefore write

χ = Re



cos

δGe

2iSt



η =Re



cos

δNe

2iSt



, (3.290)

u =Re



cos

δ Ue

2iSt



where we deﬁne

G =e

2iφ

cos

λ. (3.291)

We substitute these into (3.269), and can then determine U by taking the cross prod-

uct of (3.269)

with k, and this yields

U =

i∇ψ −sin λ k ×∇ψ

2S cos

, (3.292)

where we deﬁne

ψ =N −G. (3.293)

It follows from this that ψ satisﬁes

∇.



∇ψ +i sin λ k ×∇ψ

cos



+4S

ψ =−4S

G. (3.294)

The boundary conditions on the ocean-continent boundary are taken to be U.n =0,

and if we let n denote the outward normal away from continents, and t the tan-

gent vector at the continent when its boundary is traversed counter-clockwise, then

k ×n =t, and the no-ﬂow-through boundary condition can be written

∂ψ

∂n

−i sin λ

∂ψ

∂t

=0on∂C, (3.295)

Thus L =

, and using (3.287), S cos λ =1.

3.11 Tides and Tsunamis 203

where ∂C denotes the continental boundary. In spherical coordinate form, the

Helmholtz type equation (3.294) can be written, after some manipulation, in the

form

(1 −μ

)

∂

∂φ

∂

∂μ



1 +μ

(1 −μ

)



∂ψ

∂φ

+4S

ψ =−4S

G, (3.296)

where we deﬁne

μ =sin λ. (3.297)

(3.296) looks a little strange with the imaginary term, but in fact the equation

behaves essentially as a Helmholtz equation. Both the tidally forced (particular)

solution and the free (homogeneous) solutions have separable forms

ψ =Ψ(μ)e

iαφ

, (3.298)

where





−

α(α +1 +μ

)

(1 −μ

)



Ψ =0, (3.299)

though such solutions have limited applicability in a realistic geometry.

They do, however, point the way to understanding the solution behaviour which is

actually observed. For sufﬁciently small longitudinal wave number α, Ψ will also be

oscillatory, and the resulting waves are essentially Poincaré or gravity waves, which

we have seen before in the atmosphere (in Sect. 3.4). For large α, Ψ is exponential,

and the resultant waves are edge waves, attached to coastal boundaries, and are

Kelvin waves. In the open ocean, an oscillatory solution of the form

N ∝exp



−i(αφ +βλ)



(3.300)

corresponds to a tidal wave moving in the direction (α, β), and this is the form of

the solution locally providing N = 0.

More generally, suppose the solution ψ of (3.296) with (3.295) is computed, and

thus N is determined. We deﬁne the amplitude R

(φ, λ) and the phase t

(φ, λ)

N =R

exp(−2iSt

). (3.301)

Then the surface elevation η is given by

η =cos

δR

(φ, λ) cos





t −t

(φ, λ)



. (3.302)

The lines t

(φ, λ) = constant are called co-tidal lines; they represent the crest of

the tidal wave as it circulates round the world’s oceans. The quantity R

is called

the co-range. It is a measure of the tidal amplitude at a point.

If N was an ana-

In practice, the co-tidal phase and co-range amplitude are dimensional quantities; the phase is

measured in hours (of the lunar day), while the co-range is the elevation distance between high and

low water, and thus twice the amplitude of the underlying sine wave.

204 3 Oceans and Atmospheres

lytic function (i.e., ∇

N =0), then the co-tidal phase lines and co-range amplitude

lines would be orthogonal. This is not the case in practice, but they do intersect

transversely, and thus retain much of the same topology.

The image of a global tidal wave washing round the oceans breaks down at points

where N =0, since then the solution can no longer be approximately exponential as

in (3.300). Because N is complex, the condition N =0 requires both Re N(φ,λ)=

0 and ImN(φ,λ) =0, and thus occurs at isolated points: these are the amphidromic

points. In their vicinity, N varies linearly with φ and λ, and the local structure may

be recovered by consideration of (3.296) when N ≈ 0, i.e., ψ ≈−G:ifN = 0at

(φ

,μ

), then we put

φ =φ

+X, μ =μ

+aY, (3.303)

where we will choose a>0 later for convenience. For small X and Y ,(3.296)

implies, approximately,

(1 −μ

)

∂

∂X

∂

∂Y



1 +μ

(1 −μ

)



∂ψ

∂X

≈0, (3.304)

and this has local solutions of the form

ψ =−G

exp[iαX +βY], (3.305)

where G =G

at the amphidromic point, and

β =±

(1 −μ

)





1 +μ





1/2

. (3.306)

Note that if solutions are oscillatory in the φ direction, then they are locally expo-

nential in the λ direction, providing α>0orα<−(1 +μ

In the vicinity of the amphidromic point,

G ≈G

exp



2iX −

2μ

1 −μ



, (3.307)

and thus

N ≈ G



exp



2iX −

2μ

1 −μ



−exp{iαX +βY}



≈ i(2 −α)G

[X +iγY], (3.308)

where

γ =

a[2μ

±{α

+(1 +μ

)α}

1/2

]

(1 −μ

)(2 −α)

. (3.309)

By choosing a appropriately, we therefore have the local structure

N ∼(X ±iY) (3.310)

3.11 Tides and Tsunamis 205

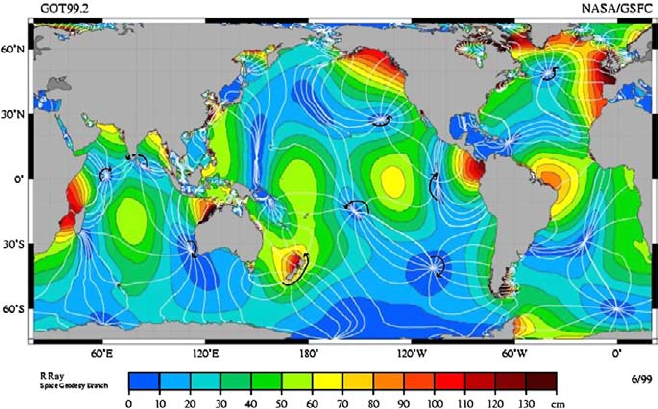
Fig. 3.13 Co-tidal map of the M

tide, deduced from Topex/Poseidon satellite altimeter measure-

ments. The colour scale indicates the amplitude of this component of the tide. White phase lines

are shown every 30°, with the heavier lines representing 0° (corresponding to when the mean moon

passes the 0° or 180° meridians). Figure courtesy of Richard Ray, NASA Goddard Space Flight

Center, and kindly provided by Helen Johnson

if β is real. In local polar coordinates X +iY =Re

iθ

, we then have

∼R, 2St

=∓θ, (3.311)

and this gives the local structure of the co-tidal lines and co-range lines in the vicin-

ity of an amphidromic point. The co-tidal lines fan out from the point, forming a

web whose circular strands are the co-range lines. At the amphidromic point the

tidal range is zero, and in its vicinity the tidal wave spins round as if glued to the

amphidromic point. The rotation is anti-clockwise if the plus sign is selected in

(3.311), and clockwise for the minus sign. Generally rotation is anti-clockwise in

the northern hemisphere and clockwise in the southern hemisphere, but not always.

Figure 3.13 shows a map of the co-tidal lines for the world oceans. The rôle of the

amphidromic points in organising the global tidal wave is clear.

If we supposed that −(1 + μ

)<α<0, then β would be imaginary, and the

value of γ is complex, but as long as the real part is non-zero, the conclusion is

essentially unaltered.

3.11.5 Tsunamis

We have not discussed the effect of shallowing of the ocean on the continental slope

which joins the continental shelf to the abyssal ocean bottom. It is fairly evident,

206 3 Oceans and Atmospheres

simply through conservation of mass, that a wave will increase in height as the

depth decreases, but for tidal waves, the wavelength is usually so large that this is of

little relevance. This is not so for tsunamis, because they are by nature much shorter

wavelength waves.

Tsunamis occur when the ocean surface is subjected to sudden disturbance. In the

Sumatran earthquake of 2004, for example, the sea ﬂoor shifted by some ﬁve metres

vertically along a horizontal fault running hundreds of kilometres, the whole process

occurring in a matter of minutes. This sudden displacement causes a localised bulge

in the ocean surface, which then propagates away from its centre as a free gravity

wave. In our dimensionless variables, the free surface is described by the free wave

equation

=∇.(h∇η), (3.312)

where it is reasonable to ignore rotation on relatively small scales. The wave speed

is (dimensionlessly) one, and in dimensional terms it is

√

gd. For an ocean of depth

four kilometres, this is 200 m s

−1

, or 720 km hr

−1

, or 450 miles per hour: pretty

fast! But in the open ocean, you notice nothing. As the wave approaches land, how-

ever, the speed decreases, and consequently, the amplitude increases. It is this effect

which causes the anthropocentrically massive tidal waves with amplitudes of tens

of metres, which are the dramatic shoreline expression of a tsunami. From the point

of view of the ocean, such massive waves are a tiny dribble at the margin.

In the Open Ocean

To describe the result of an initial localised disturbance to the ocean surface, we

write (3.312) in cylindrical coordinates, assuming constant depth h =1. Thus

=η

, (3.313)

and we will suppose that

η =η

(r), η

=0att =0. (3.314)

The initial value problem must be solved numerically, but some information is avail-

able if we limit attention to the behaviour at large r. If we deﬁne

η =

√

, (3.315)

then φ satisﬁes

=φ

, (3.316)

with leading order behaviour φ ∼φ

(r −t), thus

η ∼

(r −t)

√

. (3.317)

3.11 Tides and Tsunamis 207

To extend this result to higher order, we write r −t =ξ , and change to variables

ξ and t. A solution can then be found in the form

η ∼

(r −t)

√



r−t

(ξ) dξ

√

+··· (3.318)

(see also Question 3.14).

An alternative approach is to solve the problem (3.313) and (3.314) directly using

an appropriate transform, which is here the Hankel transform deﬁned, together with

its inverse, by

ˆg(ρ) =



∞

(ρr)g(r)dr,

g(r) =



∞

ρJ

(ρr) ˆg(ρ)dρ.

(3.319)

(A generalisation of this to Bessel functions of order ν is also available, and is

appropriate for the solution of the wave equation in cylindrical coordinates when

there is dependence on angle as well.) The point of using this transform is that



=−ρ

ˆη, (3.320)

so that the solution for η satisfying the boundary conditions is

ˆη =ˆη

(ρ) cos ρt, (3.321)

and thus

η =



∞

ρJ

(ρr) cos ρt



∞

(ρs)η

(s) ds dρ. (3.322)

We can now obtain asymptotic limiting behaviour for large t directly from this form

of the solution.

Most obviously, it seems we should write

η =



∞

sη

(s)K(r, t, s) ds, (3.323)

where

K(r,t,s) =



∞

ρJ

(ρr)J

(ρs) cos ρt dρ, (3.324)

and then evaluate K asymptotically for large t. This is not possible: integration by

parts does not work. Inspection of tables of integrals or of transforms also narrowly

fails to reveal an explicit expression for K. With some thought, this is hardly sur-

prising, since the integral deﬁned in (3.324) does not generally exist.

In writing (3.323), we essentially assumed Fubini’s theorem, which allows re-

placement of the order of integration when the integrand is Lebesgue integrable,

208 3 Oceans and Atmospheres

and in particular absolutely integrable. Evidently this is not the case. We can get

around this by deﬁning

K(r,z,s)=



∞

ρJ

(ρr)J

(ρs)e

−ρz

dρ, (3.325)

where Re z>0, and then

η(r, z) =



∞

sη

(s)K(r, z, s) ds. (3.326)

The solution is then obtained by letting z → it + 0+. The asymptotics at large t

are now straightforward. Using the limit of the Bessel function at large values of its

argument, we ﬁnd, as before, that

η ∼

(r −t)

√

, (3.327)

where

(ξ) =

√

2π



∞

√

ρ cos



ρξ −





∞

(ρs)η

(s) ds dρ. (3.328)

When r =O(1), then integration by parts of (3.325)asz →∞followed by putting

z =it yields

η ∼−



∞

sη

(s) ds (3.329)

as t →∞.

At the Coast

When a tsunami arrives at the coast, it slows down and bulks up. The slow down

is because the open ocean wave speed

√

gd decreases, and the growth of the wave

amplitude is then a consequence of conservation of mass. A simple model which

describes this follows from taking the depth to increase linearly from the shoreline,

so that in two dimensions the surface elevation satisﬁes

∂

∂x

[xη

], (3.330)

where x measures seawards distance from the shore. This has separable solutions of

the form η =e

iωt

f(x), where f satisﬁes

(xf



)



+ω

f =0, (3.331)

of which the solutions are Bessel functions J

(2ω

√

x) and Y

(2ω

√

x), or equiva-

lently the Hankel functions H

(1)

(2ω

√

x) = J

(2ω

√

x) + iY

(2ω

√

x) and

3.11 Tides and Tsunamis 209

(2)

(2ω

√

x) = J

(2ω

√

x) − iY

(2ω

√

x), and the asymptotic behaviour at large

x of the corresponding solutions η

(1)

and η

(2)

is given by

(1)

∼

(1 −i)

√

2πω

−1/4

exp



iω(t +2

√



(2)

∼

(1 +i)

√

2πω

−1/4

exp



iω(t −2

√



(3.332)

The function η

(1)

represents the incoming wave, while η

(2)

represents the re-

ﬂected wave; the general solution will be

η =



∞

−∞



I(ω)e

iωt

(1)



2ω

√



+R(ω)e

iωt

(2)



2ω

√



dω; (3.333)

I(ω) indicates the incoming wave amplitude, and R(ω) the reﬂected wave ampli-

tude.

The asymptotic form of the solutions at large x explains the basic ampliﬁcation

of the wave as it approaches the shore. The wave speed is

√

x (thus the wave slows

down) and the wave amplitude is 1/x

1/4

. Of apparent concern in this solution is that

the Hankel functions are singular as x → 0, speciﬁcally H

(1,2)

(2ω

√

x) ∼±

lnx +

O(1) as x →0, suggesting that η becomes inﬁnite as the wave reaches the shore.

This is an artefact of the implicit assumption that the wave is bounded by the ﬁxed

shoreline, and that the depth is independent of surface elevation in the shallows.

Consulting (3.266), we can see that a better model would be

∂

∂x



(x +εη)

∂η

∂x



. (3.334)

This is the sort of problem which can be treated by the method of strained coor-

dinates, when ε is small, as here. To do this, we consider η to be a function of a

strained coordinate s and time t, and we write

x =s +εX(s,τ) +···,

t =τ,

(3.335)

and then expand η as an asymptotic expansion η ∼ η

(0)

+εη

(1)

+···, whence we

ﬁnd that

(0)

−

∂

∂s



∂η

(0)

∂s



= 0,

(1)

−

∂

∂s



∂η

(1)

∂s



= 2X

(0)

−X

(0)

(3.336)

∂

∂s



X +η

(0)

−sX



(0)

