Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

340 6 Landscape Evolution

these approximations, η ≈s, we apparently do not need to specify A, and the model

reduces to

∇.(hu) =r,

|u|u =−h∇η,

=−∇.[f N]+U,

(6.25)

where N is given by (6.22). Putting δ =0, we get

≈−(h +β)∇η. (6.26)

Solving for u and substituting into the water mass equation, we can write the

system (6.25) in the form introduced by Smith and Bretherton:

∇.[qn]=r,

=−∇.[f n]+U,

n =−

∇η

|∇η|

(6.27)

where the water ﬂux is

q =h|u|=h

3/2

1/2

, (6.28)

the effective stress is

=(qS)

2/3

+βS, (6.29)

and the magnitude of the slope is

S =|∇η|. (6.30)

The dimensionless Meyer-Peter/Müller relationship, for example, can be written in

the form

f =



(qS)

2/3

+βS −τ

∗



3/2

, (6.31)

where the dimensionless critical stress is given, using (6.13) and (6.18), by

∗

ρ

[h]

. (6.32)

Using estimates μ

= 0.05, ρ

/ρ

= 2, D

= 1 mm, [h]=2cm,l = 10

d =10

m, we have τ

∗

≈0.5. We see that (6.27) forms a pair of equations for η and

q; the equation for η is essentially parabolic, while that for q is hyperbolic, although

the coupling between the equations confuses the situation.

6.5.1 Boundary Conditions

The approximation δ →0 which takes us from (6.20)to(6.27) is in fact a singular

one. This can be seen through the fact that the approximation of N by n involves the

loss of a term proportional to δ∇h, so that a Laplacian term in h (or equivalently, q)

6.5 Channel-Forming Instability 341

is missing from (6.27)

. This suggests that we ought to prescribe two conditions on

the boundary of the domain. If we consider the uplift of an island continent D with

prescribed boundary ∂D, then the natural conditions to apply are

η =0 and

∂η

∂n

=0on∂D. (6.33)

These represent the idea that the position of the coastline is known, and that the

water surface gradient becomes equal to the ocean gradient (zero) at the coastline.

The loss of the parameter δ precludes us from applying the second boundary

condition in (6.33), and in order to do so, we would require a boundary layer of

thickness δ at the boundary, over which h will change rapidly in order to satisfy

(6.33)

. This is a passive boundary layer and of little consequence. The reduced

equation (6.27)

with δ = 0 is then hyperbolic, and the natural boundary condition

on the resulting sub-characteristics is to prescribe q at their upstream end. These

occur at summits where |∇s|=0, and we expect q = 0 there, but since the q equa-

tion appears to be degenerate at the summit (∇s/|∇s| is undeﬁned), it is not entirely

obvious whether it is necessary to prescribe q at all. A similar situation applies for

a two-dimensional ridge, if the slope is smooth.

A further complication is that it can be expected that the bedload transport func-

tion f(S,q)→ 0 as both S and q → 0. In particular, since we expect q → 0ata

ridge, this suggests that the diffusion equation (6.27)

for s is degenerate, so that

smoothness may be lost at a ridge, and ∇s may be discontinuous there. In particu-

lar, it is not obvious that S →0 at a ridge. The best that can deﬁnitely be said is that

the downslope component of both water ﬂux and sediment ﬂux should tend to zero

at a ridge or a summit.

6.5.2 Steady State Solution

Our purpose is to study conditions under which uniform overland ﬂow is unstable,

and the simplest situation in which we can do this is when the basic steady state ﬂow

is one-dimensional. Therefore we consider a basic state consisting of a symmetric

hillslope inclining down towards a ﬁxed boundary, as indicated in Fig. 6.3.Wetake

the divide to be at x =0 and the margin at x =1, and we solve the one-dimensional

version of (6.27)inx>0, assuming that η

< 0, thus −∇η/|∇η |=i, where i is the

unit vector in the x-direction:

∂q

∂x

=r,

∂f

∂x

=U, (6.34)

and the solution with zero ﬂuxes at the ridge is

q =rx, f =Ux. (6.35)

More generally,

q =R =



rdx, f =W =



Udx, (6.36)

342 6 Landscape Evolution

Fig. 6.3 One-dimensional

hillslope geometry

if we suppose rainfall r and uplift U to be functions of the distance x from the

divide. If we take the Meyer-Peter/Müller transport law (6.31), for example (but

written in terms of h and S =−η



(x), then we ﬁnd that h and η are given by

h +β

∗

2/3

,η=



. (6.37)

If τ

∗

and β are small and can be ignored, these are simply

h ≈

1/3

,η≈



Wdx

, (6.38)

and the slope is

S =

. (6.39)

The particular choices of constant uplift and rainfall then give

h ≈

2/3

,S=

, (6.40)

and the slope is constant. Note that in this case the hillslope is not zero at the divide,

and this is generally true if the yield stress is non-zero, since the sediment transport

is positive for all x>0.

A crucial feature of the hillslope for stability purposes is the sign of the slope cur-

vature, or the sign of S



. The shape of the hillslope depends on the bedload transport

function f(S,q), and in general must be found numerically. For constant rainfall

and uplift, the sign of the curvature can be ascertained analytically, however. Differ-

entiating f with respect to x, we ﬁnd (using (6.35)),

∂f

∂S



=f −q

∂f

∂q

. (6.41)

Supposing always that ∂f /∂ S > 0, we have S



> 0 if and only if f −q∂f/∂q > 0.

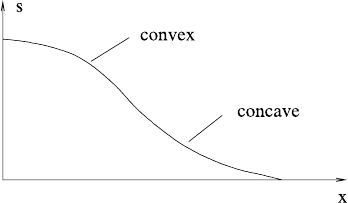
We deﬁne concavity and convexity of hillslopes as shown in Fig. 6.4, thus convex

slopes have S



< 0, concave ones have S



> 0. Thus convexity or concavity of a

hillslope is determined only by the dependence of the bedload transport on water

ﬂux, in conditions of constant rainfall and uplift.

In particular, and absolutely confusingly, functions which are mathematically

convex, so that, in particular, ∂f /∂ q > f /q everywhere, lead to (geomorpholog-

ically) concave hillslopes, and vice versa. Worse, a mathematician would call

the ‘concave’ portion of the graph in Fig. 6.4 convex. Worse still, the criterion

∂f /∂ q > f /q is satisﬁed by mathematically convex functions, but not all such func-

tions are mathematically convex everywhere. It is best to forget the mathematical

6.5 Channel-Forming Instability 343

Fig. 6.4 Convexity and

concavity

deﬁnitions; geomorphologically concave transport laws lead to similarly shaped

hillslopes.

It is fairly evident that convex or concave hillslopes can be formed independently

of f , if rainfall or uplift are spatially varying. For example, the Meyer-Peter/Müller

law with β =τ

∗

=0issimplyf =qS, so that f

=f/q, and the slope is constant

(as we found) for constant r and U . When they vary, S =W/R, and by appropriate

choice of r and U , we may have S



being positive or negative in different regions.

6.5.3 Uplift and Denudation

Before we begin our stability analysis of the purely x-dependent state, we should

put our model into a physical context. We pose a constant (or perhaps spatially de-

pendent) rate of uplift and purely ﬂuvial erosion mainly in order to establish a clean

mathematical problem. In reality, orogenic episodes are more likely to occur in tran-

sient events. For example India runs into Asia some 50 million years ago, and starts

building the Himalayas, a process which is still continuing. So while our model

might apply in the early phases of the orogeny, there is certainly never a steady

state, and the ﬂuvial drainage systems which no doubt grew in the early phases of

the orogeny did so as instabilities formed on a slowly evolving uplifting topography.

Thus, while we emphasise the instability of a steady state as a mathematically pre-

cise way of analysing the problem, this is not really the ‘right’ problem. Equally and

more obviously, ﬂuvial erosion becomes irrelevant at greater topographic heights,

when glacial erosion and landslides become the erosive mechanisms of choice.

As regards instability, this issue is not a real barrier to understanding, because

instability, when it occurs, does so rapidly, so that to all intents and purposes we

can still do stability analysis even when the background hillslope topography is

changing slowly. In that case, the form of the topography is determined essentially

by tectonic processes, and not by the model proposed here. For example we might

suppose that tectonic compression could form a series of sinusoidal folds transverse

to the direction of compression; such folds are unstable to channel formation in their

valleys, as indeed we would expect.

344 6 Landscape Evolution

6.5.4 Geomorphically Concave Slopes are Unstable

We study the linear stability of the one-dimensional steady state (6.35) of the gov-

erning equations (6.27). We denote the steady state with a subscript zero, and will

focus on the region x>0, where the slope η



< 0; to extend the discussion to the

other side of the hillslope, we simply note that the basic solutions for q and f there

are even extensions of those in (6.35). Unless otherwise stated, we will assume that

r and U are constant.

Denoting perturbations by an overtilde, thus

η =η

+˜η, (6.42)

and so on, we ﬁnd

∇η =η



i +∇˜η,

S =|∇η|=S

−˜η

...,

(6.43)

where S

=−η



. From these, it follows that the downslope unit vector is

n =i −

˜η

j +···, (6.44)

where j is the unit vector in the transverse y direction.

This gives the linear approximation for n. If we perturb f and q by quantities

and ˜q, then we obtain, on linearising the equations,

∂ ˜q

∂x

∂

˜η

∂y

∂ ˜η

∂t

∂

∂x



∂ ˜η

∂x



−f



˜q +



−f



∂

˜η

∂y

(6.45)

where f

= ∂f /∂ S , f

= ∂f /∂ q , and f



denotes the x derivative of f

, all these

quantities being evaluated in the basic steady state (we omit the subscripts zero for

convenience).

It is worth pausing with these linearised equations. We see in the second that it

is of diffusive type, but that the apparent diffusion coefﬁcient in the y direction can

be negative, and is so if f

>f/q; returning to (6.41), we see that this condition is

met precisely if the steady hillslope is geomorphologically concave (when r and U

are constant).

Such an assessment might seem premature, since the term in ˜q is coupled (via

(6.45)

) to another ˜η

term. But as we shall see, it is essentially accurate; as an

example, if the bedload transport function is taken as f ∝ q

for some positive

exponent n, then f



=0, and the conclusion above is precise.

We use normal mode analysis, and write ˜η and ˜q in the form

˜q =φ(x)e

iky+σt

, ˜η =ψ(x)e

iky+σt

; (6.46)

6.5 Channel-Forming Instability 345

from these deﬁnitions it follows that



=−

qψ

σψ =[f



]



−(f

φ)



−

fψ

(6.47)

The boundary conditions we would like to apply to these equations are

φ =f



=0atx =0,

ψ =0atx =1.

(6.48)

The condition on φ at the ridge x = 0 follows from the prescription of zero water

ﬂux there; the condition on ψ at x =1 follows from ﬁxing the (sea-level) topogra-

phy at the margin.

The condition on ψ at x =0 represents the condition of zero sediment ﬂux at the

ridge, and merits some discussion. The actual condition we require is that f(S,q)=

0 (or more properly f(S,q)n

= 0) at x =0. Since we require q = 0 there, this is

equivalently f(S,0) =0, which deﬁnes a constant, say S =S

.IfS

=0 (as for the

Meyer-Peter/Müller law with non-zero τ

∗

and β), then the linearisation in (6.43)is

valid at x =0, and the appropriate condition is indeed that given in (6.48) (with the

included). If f

=0, then ψ



=0atx = 0. If, on the other hand, f

=0atx =0,

then the second equation in (6.47) has a degenerate second derivative in ψ (i.e., the

coefﬁcient of the highest derivative is zero at x = 0), and it is well known in such

circumstances that no speciﬁc boundary condition for ψ following from (6.47)

can

be prescribed, beyond requiring that ψ



be bounded. This needs to be borne in mind

when speciﬁc transport laws are used.

The situation is more complicated when S

= 0. In this case, linearisation as in

(6.43) fails at x = 0, and we have n =−∇˜η/|∇˜η|. The condition |∇˜η|=0 would

imply both ˜η

=˜η

=0, and thus ψ =ψ



=0atx =0, two conditions rather than

one. However, we also have n

=−˜η

/|∇˜η|, so that the condition fn

=0 is satis-

ﬁed by the single requirement that ˜η

=0, and thus ψ



=0 in the linear approxima-

tion. Again, (6.47)

applies since the (linearised) perturbation of f is zero indepen-

dently of (bounded) ψ



if f

=0, despite the fact that the slope linearisation breaks

down at x =0 in this case.

We eliminate ψ from (6.47) to obtain the third order system

σS



















φ)



−





, (6.49)

with boundary conditions

φ =f









=0atx =0,



=0atx =1.

(6.50)

Instability occurs if, for any wave number k, the real part of σ is positive. It is

straightforward to show (see Exercise 6.8) that for one-dimensional perturbations

downslope (i.e., k =0), σ<0. Therefore instability requires k>0, i.e., lateral per-

turbations.

346 6 Landscape Evolution

To get some idea of the behaviour of solutions, suppose that the coefﬁcient func-

tions of x in (6.49)(i.e.,q, S, f , f

and f

) are taken as (positive) constants.

The

three independent solutions are then φ = constant, and φ = exp[±(Λ/f

)

1/2

kx],

where we deﬁne

Λ =

−



−



. (6.51)

The linear combination of the three solutions which satisﬁes the two boundary con-

ditions at x =0is

φ =sin



−Λ



1/2



, (6.52)

and the condition on σ to satisfy the ﬁnal boundary condition at x =1 requires that

Λ<0, and k(−Λ/f

)

1/2

=(m +

)π for integral m, and thus

σ =



−



−f



m +



. (6.53)

If we take k = 0, then σ<0, consistent with our earlier statement that one-

dimensional downslope perturbations are stable. The most unstable mode when

k =0 is that for m =0, and (6.52) thus suggests instability if

−

4qk

, (6.54)

which is identical to our earlier statement following (6.45), as k →∞.

Ill-posedness

When the criterion for instability is satisﬁed, the growth rate σ ∼ k

, and this is

the hallmark of a process with negative (lateral) diffusion, and the resultant un-

bounded increase of σ at high wave number implies ill-posedness. It suggests that

there is something fundamentally wrong with this approximate model, and that di-

rect numerical simulations of (6.27) are ill-advised. As we hope that the model is

not physically unsound, it is natural to expect that one of the simplifying assump-

tions we made has removed a stabilising term which can dampen high wave number

modes. The obvious candidate is the parameter δ, since as we have seen, its neglect

is singular, and that leads to a change of type in the equations.

There is a beneﬁcial effect of this ill-posedness, however. The solution obtained

above assumes all the coefﬁcient functions are constant, but we would like to extend

the result to x-dependent coefﬁcients. This is not generally possible, but the fact

that the most unstable modes have short wavelength implies that, at least for these

modes, a WKB analysis is possible, since at high k, the coefﬁcient functions are

relatively slowly varying. We now show how to do this.

Note that in this case we avoid all the complications of degeneracy at x =0.

6.5 Channel-Forming Instability 347

6.5.5 WKB Approximation at High Wave Number

We use the deﬁnition of Λ in (6.51) so that (6.49) can be written in the form

Λφ





















, (6.55)

and we seek solutions in the limit k  1 which satisfy the boundary conditions in

(6.50). In the (ﬁrst order) geometric WKB approximation, the solutions are given

approximately by

∼exp







SΛ



∼exp



±k







1/2



(6.56)

and we shall suppose that Λ is either positive or negative throughout. The more

interesting case where its sign changes is treated in the following section.

An additional complication arises because of the fact that q → 0asx → 0in

(6.55). It also independently occurs if f

→ 0asx →0, which is the case for the

Meyer-Peter/Müller relation. Because of these degeneracies, the WKB solutions in

(6.56) are not uniformly valid near x =0. Despite this, we shall for ease of expo-

sition suppose that they are. As we might expect, the details at the summit do not

appear to signiﬁcantly affect the instability criterion; further consideration of the

matter is deferred to Question 6.9.

A suitable choice of transport function allows the assumption of uniform validity

of the WKB solutions to be made explicit. If we suppose

f =q

1−α

=τ

3α/2

(3−5α)/2

, (6.57)

then for any α ∈(0,

), we have a physically meaningful transport law with f

> 0

and S/q ﬁnite at x =0 (and in fact, constant) so that the second boundary condition

in (6.50) reduces to



=0atx =0. (6.58)

For purposes of illustration, we shall make this assumption, as it provides a direct

comparison with the previous, constant coefﬁcient analysis.

The function φ

is slowly varying, and follows from a regular approximation

to (6.55); it generalises the constant solution for the constant coefﬁcient version of

(6.49); the functions φ

are rapidly varying, and constitute the generalisation of the

sinusoidal solutions of the constant coefﬁcient model.

The solution of the equation is thus approximately

φ ∼U

−

. (6.59)

348 6 Landscape Evolution

Satisfaction of the boundary conditions φ =φ



= 0atx = 0 and φ



= 0atx = 1

requires

−

=0,



(0) +k







−

) =0,



(1) +k





1/2





exp









1/2



−U

−

exp



−k







1/2



=0.

(6.60)

Since k is large, the ﬁrst two of these give U

≈ 0, U

≈−U

−

. Evidently we will

require Λ<0, and the solution can be written (taking U

= 1/2i without loss of

generality) as

φ =sin







−Λ



1/2



, (6.61)

and the condition φ



=0atx =1 implies





−Λ



1/2

dx =

(2m +1)π

, (6.62)

where m is an integer. (6.61) is a simple generalisation of (6.52), and the eigenvalue

condition (6.62), written in the form





−



−



1/2

dx =



m +



, (6.63)

is a simple generalisation of (6.53).

If f

≤f/q everywhere, then (6.63) implies σ<0, and the (convex) hillslope is

stable. However, if f

>f/q everywhere, then it is clear that there will be positive

values of σ , since for large k, the right hand side of (6.63) can approximately take

any positive value. Thus the maximal growth rate for f

>f/q will be

σ ≈k

min

[0,1]



−



. (6.64)

Again the growth rate is unbounded at small wavelength.

This is not the end of the story, because the nature of the instability via a negative

lateral diffusion coefﬁcient suggests that if f

>f/q anywhere, then the hillslope

will still be unstable. If this is the case, then Λ must change sign, and the WKB

analysis must be modiﬁed to allow for turning points, where Λ = 0. This we now

do.

6.5.6 Turning Point Analysis

We will consider the simplest case in which there is a single turning point, at x

,say,

and we suppose that Λ>0 upslope in x<x

, and Λ<0 downslope in x>x

.At

6.5 Channel-Forming Instability 349

the onset of instability (σ = 0), this corresponds to a locally stable (convex) slope

at the ridge, and a locally concave (unstable) slope at the margin, as illustrated by

Fig. 6.4. The solution is much as before, but now we need to include the second order

correcting term of physical optics in the approximations for the rapidly varying

solutions.

In x<x

, the slowly varying solution is

∼exp







SΛ







,x<x

, (6.65)

and the physical optics (two term) approximations for the rapidly varying solutions

can be taken as

∼

1/4

SΛ

3/4

1/2

exp



±k







1/2



,x<x

; (6.66)

these can be compared with (6.56).

In x>x

, we take the corresponding solutions as

∼exp







SΛ







,x>x

, (6.67)

and

∼

1/4

S|Λ|

3/4

1/2

exp



±ik





|Λ|



1/2



,x>x

. (6.68)

The solution upslope is

φ =U

−

,x<x

, (6.69)

and that downslope is

φ =D

−

,x>x

, (6.70)

but both approximations break down in the vicinity of x = x

, where Λ = 0. The

object is to solve the problem in this transition region, in order to provide connection

formulae relating U

to D

; the eigenvalue relation for Λ, and thus σ , can then be

established.

The relevant coordinate in the transition region is ζ , deﬁned by

x =x

−



|Λ





1/3

2/3

, (6.71)

where Λ



is the (negative) gradient of Λ at x

, i.e.,

Λ ≈−|Λ



|(x −x

). (6.72)

Note that ζ points upslope. Evaluating the outer solutions as x → x

, we ﬁnd, for

x<x

(ζ>0),

∼a

p−1



1 +O



−2/3



, (6.73)