Fowler A. Mathematical Geoscience
Подождите немного. Документ загружается.


370 6 Landscape Evolution
make an additional assumption that S, H and therefore also Q vary slowly with x.
In that case (bearing in mind that α is small),
a ≈−
αQS
D
exp
−
D(x −x
0
)
QS
−1
. (6.196)
If D is small, we can take a Taylor expansion of (6.196), and then
a ≈α(x −x
0
) −
αD
QS
(x −x
0
)
2
2
···, (6.197)
and thus
1
α
∂H
∂T
=QS +α
(x −x
0
)
2
2
D, (6.198)
with relative error of O(α). The small diffusion term is retained because it represents
a singular approximation.
Equation (6.198) perhaps represents the simplest version of the channel evolution
equation in detachment limited conditions. It is similar to (6.194), but importantly
the source term does not rely on the convexity (or concavity) of the hillslope. The
derivation of a pair of equations for channel profile and channel flux analogous to
(6.177) and (6.178)isleftasanexercise.
6.7.3 Headward Erosion
More or less, the Smith–Bretherton model, or others of similar type, gives us a recipe
to evolve a landscape. It is then a computational matter to compare the results of
such evolutions with actual landscapes. In our discussion, we have jumped abruptly
from the initial instability which will form rills to the evolution of deep channels in
a mature landscape.
In a computational experiment (but these have yet to be done), an initially up-
lifting island continent will first develop rills at the margin, where the slope bound-
ary condition forces concavity. In conditions of plentiful sediment supply, channels
cannot apparently form on lower slopes, and it is not until detachment limitation
becomes effective that channels will grow, attaining a locally stable equilibrium
shape described by steady solutions of, for example, (6.198). The outer hillslope
then evolves according to (6.27), with the channel flux and long profile being deter-
mined by two equations similar to (6.177) and (6.178). Conditions on the water flux
¯
Q and the hillslope S at the channel head are that they are determined by continuity
with the outer flow. Specifically, the channel head is a singularity for the hillslope,
in the sense that upstream of the head, the flow vectors n must all converge at the
channel head, as indicated in Fig. 6.7. In this case, there is a non-zero water flux at
the channel head. The alternative possibility is that only a single flow line enters the
channel, ∇η is smooth at the head, and the water flux is zero there.
At least for (6.177), the condition
¯
Q =0atx =x
H
(the channel head position)
provides both an initial condition for
¯
Q, and a condition on the channel slope S
0
.
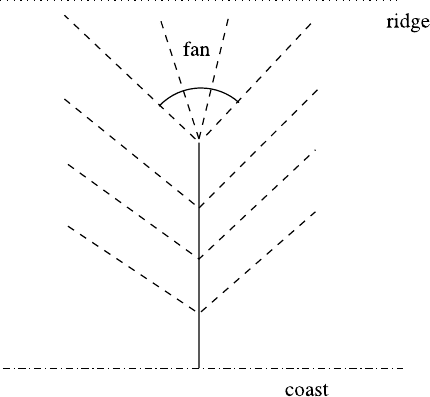
6.8 Notes and References 371
Fig. 6.7 Schematic
indication of flow line vectors
n on the hillslope if the head
channel flux is non-zero. A
fan of flow lines reaches the
channel head
The other condition on the channel profile is that η
0
be continuous with the hillslope
at the head. Thus for zero head flux, the channel head position (and thus also its rate
of migration) is determined by the extra condition on η
0
.
Whether or when the situation depicted in Fig. 6.7 can occur mathematically
is less clear. The position of the channel head is then apparently determined by
the condition of intersection of a fan of characteristics of the hillslope water flow
equation. It seems difficult for the hillslope to maintain this ability, so that the zero
flux may be the preferred option.
6.7.4 Side-Branching
The other ingredient for a computational model is the formation of side branches.
This is equivalent to the problem of channel initiation. As a channel develops, the
hillslope on either side will steepen, resulting in instability, rill formation, and even-
tual channel development. As for a primary channel, the model suggests that tribu-
tary channels will form when sediment is depleted sufficiently for detachment lim-
ited transport to be appropriate.
6.8 Notes and References
Hillslope Processes The Davisian cycle of erosion was developed by Davis to-
wards the end of the nineteenth century (e.g., Davis 1899), and the rise and fall of the
theory and its historical context has been voluminously described by Orme (2007),
372 6 Landscape Evolution
who incidentally gives a much wider description of the early history of the geo-
sciences in general. A more model-based discussion of uplift and erosion is given
by Willett and Brandon (2002).
Description of erosion and sedimentation is given in the books by Julien (1995)
and Selby (1993), for example. Julien’s book is largely concerned with stream flows
and their sediment transport, while Selby’s is more concerned with hillslope ero-
sion. Between them, they give a good survey of the physical processes of erosion
and transport which occur in different types of landscape. Various relationships for
sediment transport discussed in the text are given by Shields (1936), Meyer-Peter
and Müller (1948) and Van Rijn (1984).
The development of geomorphometry, and in particular the various ordering sys-
tems and power-law relationships, are described by Hack (1957), Horton (1945) and
Strahler (1952). The book by Turcotte (1992) gives a wide-ranging description of
many geophysical contexts in which power laws, and thus fractal processes, arise.
It may be fair to say that a process-based descriptive model which can predict such
features has not yet been developed.
Channel-Forming Instability The seminal paper in the theory of channel devel-
opment is that by Smith and Bretherton (1972). As discussed above, the St. Venant–
Exner model is studied (suspended load is neglected, E =D =0), and instability is
found to occur for concave surfaces (centre of curvature above ground).
Smith and Bretherton’s result was predicated on the basis of the negative diffu-
sion coefficient manifested in (6.45), for example. Loewenherz (1991) carried out
a formal linear stability analysis using normal modes, and extended this to con-
vex/concave slopes using WKB theory at high wave number. She also considered
the problem of regularisation as k →∞, by introduction of a (fairly arbitrary) mod-
ification to the transport law.
Later (Loewenherz-Lawrence 1994), she treated the whole problem again, but
now starting from the hydrodynamic theory, much as we have done here. The rôle
of the parameter δ (representing film thickness) becomes critical. She also takes a
more general form of sediment transport law,
Q
b
=f
D
m +f
A
n, (6.199)
where f
A
and f
D
signify advective and diffusive fluxes, and m =−∇s/|∇s| is the
downslope unit vector. The result of this is that perturbations are damped at large
wave number, essentially for the same reason as described here.
Izumi and Parker (1995, see also 2000) were also concerned with the lack of
wavelength selection in the Smith–Bretherton theory, and sought to rectify this by
explicitly including the yield stress in the transport law. They find a selected wave-
length of 33 m in their (hydrodynamic) theory, which they compare favourably (in
order of magnitude) with observed mature spacings in the range 60–130 m. In our
discussion of the stabilising effect of the slope parameter β, we similarly find a
preferred wavelength (see (6.120) and Question 6.11) of order l/k ∼ δ
3/4
l ∼18 m,
for l = 100 km and δ = 10
−5
. Izumi and Parker (1995) also share the idea in their

6.8 Notes and References 373
discussion that hillslope development will be accompanied by a coarsening pro-
cess, whereby drainage basins will gradually enlarge, with larger streams capturing
smaller ones.
12
Relatively few authors have attempted to describe the evolution of channels
within the confines of a general hillslope evolution model. One example of this type
of model is that of Kramer and Marder (1992), also discussed by Fowler (1997,
pp. 266 ff.), and see Question 6.1. This model is essentially that of Eqs. (6.2)–
(6.4), with acceleration neglected in the momentum equation (small Froude num-
ber), bed abrasion included but uplift omitted. Sediment transport is modelled by
atermq
b
∝−∇s, thus sediment moves down the bed slope. This model exhibits
channel-forming instability which does not depend on hillslope curvature. Kramer
and Marder discuss possible nonlinear solutions for these channels. With certain
assumptions (see Question 6.1), one can derive a nonlinear evolution equation for
(dimensionless) channel depth H in the form
H
t
=H
3/2
−1 +
H
3/2
H
Y
Y
, (6.200)
where Y is the cross stream spatial variable. Depending on the boundary conditions,
this model allows finite amplitude steady states. A similar nonlinear development
for the Smith–Bretherton model as discussed in this chapter was carried out by
Winstanley (2001).
Smith et al. (1997a, 1997b) use what we have called the ‘outer’ approximation
(essentially (6.27) with no uplift) to represent mature hillslope evolution, and find
certain classes of separable solutions, whose stability they then examine. They also
compute solutions numerically, but a representation of channels is not included.
A recent paper by Smith (2010) gives a thorough review of the development of the
continuum-based theories, and discusses the instability theory in great detail.
WKB Theory WKB theory was applied by Loewenherz (1991) and Loewenherz-
Lawrence (1994) to the study of rill-forming instability of flow over erodible slopes.
Succinct treatments of the theory are in the books by Carrier et al. (1966) and Bender
and Orszag (1978). The basic idea is very simple. The equation
w
+k
2
q(x)w = 0, (6.201)
where w
= dw/dx and k is large, has solutions exp[±ikq
1/2
x] if q is constant.
These oscillate rapidly if q>0. If q varies, we can still expect rapidly oscillating
solutions, but the period will vary. The ansatz
w ∼exp[kw
0
+w
1
+···] (6.202)
and subsequent expansion in powers of k lead to the solutions
w
0
=±i
x
q
1/2
dx, w
1
=−
1
4
ln |q|, (6.203)
12
Such coarsening is familiar in the equally dendritic environment of a solidifying alloy, see for
example Marsh and Glicksman (1996).

374 6 Landscape Evolution
and thus
w ∼
1
|q|
1/4
exp
±i
x
q
1/2
dx
. (6.204)
The one term approximation is called geometric optics, the two term approximation
(i.e., as in (6.204)) is called physical optics. Evidently, something unusual happens
if q goes through zero. Near such transition points, w approximately satisfies the
Airy equation, and the resulting Airy function solutions enable a connection to be
made between oscillatory solutions (where q>0) and exponential solutions (where
q<0) on either side of the transition point.
The Equation φ
−ζφ
+(p −1)φ =0 The properties of the solutions to this
equation have been extensively investigated by Bill Reid in connection with asymp-
totic solutions of the Orr–Sommerfeld equation. See for example Reid (1972) and
Lakin et al. (1978), as well as the book by Drazin and Reid (1981). The asymptotic
properties used here are given succinctly by Hershenov (1976) and Baldwin (1985).
Nonlinear Diffusion and Blow-up for H
T
=H
3/2
+(H
1/2
H
Y
)
Y
Properties of
the solutions of this equation (and generalisations) are extensively discussed in the
book by Samarskii et al. (1995). If we solve the equation of the heading in an in-
terval [−L, L], with H = 0on±L and H ≥ 0atT = 0, then the solution blows
up in finite time if L>π/
√
6 (see Question 6.13). In general, solutions of compact
support remain so, thus the margins (where H reaches zero) move at finite speed,
as expected for such degenerate diffusion equations. One can even construct certain
exact solutions which blow up.
So why do we claim that blow-up does not occur? The proof of blow-up involves
the essential assumption that H
1/2
H
Y
=0 when H =0, thus there is no efflux of H
from the channel, and because of this and the superlinear source, it is almost obvious
that blow-up will occur. In our case, H
1/2
H
Y
=0 at the margins, and the production
of H can be balanced by its loss at the margins. Indeed, the extra integral constraint
Y
0
−Y
0
H
3/2
dY =
¯
Q which we pose to complete the formulation of the problem for
H almost implies boundedness of the solution for all time. Fowler et al. (2007)
provide detailed numerical analysis of the equation, which shows that the steady
state is globally stable, and the solution attains compact support instantaneously,
even if the initial condition has infinite support.
Lattice Models As Willgoose et al. (1991) remark concerning hillslope models,
“the difficulty of the problem is such that the number of researchers that have at-
tempted to unify the geomorphology and the hydrology is small”. And in fact, the
subject took a right angled turn at the beginning of the 1990s. Faced with a relatively
simple pair of equations for hillslope and water flow, and a successful characterisa-
tion of the hillslope instability criterion, efforts to compute the solutions directly
simply foundered. Kramer and Marder (1992) state the consequence as follows:
The computer time to study [the model] on a large scale is formidable. In order to learn
about larger-scale features of river networks, we have abstracted from our previous work a
simple lattice model . . .

6.9 Exercises 375
Essentially, this has been the standard approach in the last 20 or so years. Kramer
and Marder used a lattice with rules based on sediment and water conservation to
prescribe transport between adjacent nodes in each time step. In the lattice model,
channels are interpreted to be where flow is maximum. In Willgoose et al.’s (1991)
approach, a channel indicator function is used as an artificial switch to decide when
and where a channel appears.
The direction in which these lattice models have gone is exemplified by the book
of Rodríguez-Iturbe and Rinaldo (1997), which relentlessly emphasises the fractal
character of river networks, and the lattice-type models which simulate them. A
related ‘principle’ which is sometimes invoked is that of optimality, the idea that
river networks organise themselves in order to minimise energy expenditure. As
with the long-standing idea that turbulent convection maximises heat transport, there
appears to be no deductive basis to this idea.
Howard (1994) also uses a cellular model to compute simulations, but he empha-
sises the importance of detachment limited transport: indeed, he argues that fluvial
erosion of natural slopes and headwater channels is dominantly detachment limited.
This idea nicely dovetails with our apparently similar deduction from the (gener-
alised) Smith–Bretherton transport model. However, his model does not explicitly
model weathering (i.e., what we have called abrasion) in the way described here.
Tucker and Slingerland (1994) use a cellular model to simulate landscape evo-
lution, with a view to explaining the formation and retreat of escarpments in high
elevation rifted continental margins, such as in southern Africa or eastern Australia.
Their model, in its differential equation form, is similar to that presented here, inso-
far as the weathering rate (A) is specifically included, so that conservation of rock
and conservation of sediment provide two equations equivalent to (6.8) and (6.6),
and a variable equivalent to sediment thickness a is included. As here, the weather-
ing rate is a monotonically decreasing function of a. In their simulations, they note
that there is a profound difference between transport limited and supply (detach-
ment) limited erosion, with the latter providing a mechanism for scarp formation
and retreat. A recent survey of lattice-type models is given by Willgoose (2005).
6.9 Exercises
6.1 Kramer and Marder (1992) propose a model for hillslope evolution as follows.
With the same notation as in this chapter, their equations for water flow and
hillslope evolution are
∂h
∂t
+∇.(hv) =r,
∂s
∂t
=−
ρ
w
g
P
0
h|v|[1 +|∇s|
2
]
1/2
[1 +|∇η |
2
]
+ν∇.
h|v|∇s
,
η =s +h,

376 6 Landscape Evolution
where ρ
w
is water density, P
0
is an erodibility constant, and the water velocity
is
v =−
(2g)
1/2
h
1/2
∇η
[1 +|∇η |
2
]
1/2
.
Compare this model with that derived in the text. Is it possible to derive this
model by making suitable constitutive assumptions?
Non-dimensionalise the model using scales
h ∼[h],η,s∼[H ], x ∼l, v ∼[v],r∼[r],t∼[t],
where [H ], l and [r] are prescribed. Show that by suitable choice of [t], [h]
and [v], the model can be written in the non-dimensional form
∂h
∂t
=∇.
h
3/2
∇η
[1 +ε
2
|∇η |
2
]
1/2
+r,
∂s
∂t
=−
βh
3/2
|∇η |[1 +ε
2
|∇s|
2
]
1/2
[1 +ε
2
|∇η |
2
]
3/2
+γ ∇.
h
3/2
|∇η |∇s
[1 +ε
2
|∇η |
2
]
1/2
,
η =s +δh,
and show that the parameters are given by
β =
ρ
w
g[h]l
P
0
[H ]
,γ=
ν[h]
l
,ε=
[H ]
l
,δ=
[h]
[H ]
,
where
[h]=
l
2
[r]
(2g)
1/2
[H ]
2/3
.
Use values ν = 0.1 and P
0
= 3 ×10
10
kg m
−1
s
−2
along with other typical
values for [H], l and [r] to find estimates for ε, δ, β and γ . Deduce that the
model may reasonably be approximated as
∂h
∂t
=∇.
h
3/2
∇η
+r,
∂s
∂t
=−βh
3/2
|∇η |+γ ∇.
h
3/2
|∇η |∇s
,
explaining why the terms in β and γ are important.
Now suppose that r = 0 and a uniform flow descends a uniform slope in
the x direction. Show that an exact solution representing this exists in the form
η =−βt −x, h =1.
Show further that if η =−βt −x, then the sediment transport equation admits
solutions in which h = h(y, t), where y is the cross stream coordinate. By
choosing a suitable rescaling of y and t, show that h satisfies the equation
∂h
∂T
=h
3/2
−1 +
∂
∂Y
h
3/2
∂h
∂Y
.
6.9 Exercises 377
Show that the uniform solution h =1 is unstable, and show that steady chan-
nels h =h(Y ) exist satisfying h(±∞) = 0, where
h
2
Y
=
K
h
3
+
4
5h
1/2
−
1
2h
,
and K is a non-negative constant. Show that solutions of this equation reach
zero at a finite value of Y =Y
0
, say, and show that the maximum depth h
m
(at
Y =0) is defined (uniquely) in terms of the non-negative K by
K =
1
2
h
4
m
−
4
5
h
5/2
m
.
Show that a unique channel shape is identified (by its maximum depth) if the
channel flux Q =
Y
0
−Y
0
h
3/2
dY is prescribed, and show in this case that h
m
is
determined by
Q =2h
11/4
m
√
10
1
0
u
3
du
[5h
3/2
m
(1 −u
4
) −8(1 −u
5/2
)]
1/2
.
Does this determine h
m
uniquely?
6.2 In two-dimensional laminar flow of a film of depth h down an incline, the
horizontal velocity u satisfies
μ
∂
2
u
∂z
2
=ρ
w
gη
(x),
where μ is the viscosity, x is the downstream coordinate and z = η is the top
surface. Suitable boundary conditions for the flow are of no stress, ∂u/∂z =0,
at z = η, and no slip, u = 0, at z = s =η −h. Assuming h is constant, show
that the mean velocity is
¯u =−
ρ
w
gh
2
η
3μ
,
and explain why the horizontal momentum equation for averaged laminar film
flow can be taken to be of the form
u
t
+(u.∇)u =−g∇η −
ku
h
2
,
where k =
3μ
ρ
w
. Show also that the boundary stress is
τ =
ρ
w
ku
h
,
and that mass conservation for water flow takes the form
h
t
+∇.(hu) =r,
where r is rainfall.
Non-dimensionalise the momentum and mass flow equations for water ap-
propriately using the laminar definition of the stress, and show that the corre-
sponding velocity and depth scales are
[h]=
r
D
l
2
k
gH
1/3
, [u]=
r
2
D
lgH
k
1/3
,

378 6 Landscape Evolution
where l is the topographic horizontal length scale and H is the topographic
elevation scale. Use values r
D
∼ 1my
−1
, l ∼10
5
m, k ∼ 3 ×10
−6
m
2
s
−1
,
g ∼10 m s
−2
, H ∼ 10
3
m, to find typical values for [u] and [h]. Hence show
that the Reynolds number for the flow is Re =[u][h]/k ∼10
3
.
Show that the effective dimensionless driving stress for sediment transport
is
τ
e
=u −γ ∇s,
where
γ =
ρ
sw
gD
s
H [h]
ρ
w
lk[u]
.
Using the additional values ρ
sw
/ρ
w
∼1.6, D
s
∼1 mm, show that γ ≈0.34.
If the yield stress is defined by
τ
c
=μ
c
ρ
sw
gD
s
,
show that the dimensionless yield stress is
τ
∗
c
=
μ
c
γl
H
≈1.7,
if μ =0.05.
Hence show that an approximate model of hill slope erosion is provided by
the dimensionless equations
−∇.
h
3
∇s
=r,
s
t
=U +∇.
F(τ
e
)∇s
,
τ
e
=
h
2
+γ
S,
where S =|∇s|, and F is the dimensionless sediment transport rate.
6.3 Suppose that in the dimensionless model for hillslope erosion
δεh
t
+∇.(hu) =r,
δF
2
δεu
t
+(u.∇)u
=−∇η −
|u|u
h
,
η =s +δh +δνa,
δνa
t
+∇.Q
b
=A,
s
t
=−A +U,
τ
e
=|u|u −β∇s,
rainfall occurs in brief, severe storms. Suppose that the rainfall intensity during
these storms is r
S
, so that in dimensionless terms we have (why?) r ∼1/ω for
periods of O(ω) at intervals of O(1), where ω = r
D
/r
S
1, r
D
being the
scale for the rainfall.
Show that between storms, s
t
≈U , while during the storms, the approxima-
tions δ,ε →0 can be made if δε ω
2/3
and δF
2
ω
2/3
. Use the definitions
6.9 Exercises 379
ε =
U
D
r
D
,δ=
[h]
d
,F
2
=
[u]
2
g[h]
, [u]=
gr
D
d
f
1/3
, [h]=l
fr
2
D
gd
1/3
,
to show that
δF
2
ω
2/3
=
r
S
f
√
gd
2/3
,
and
δε
ω
2/3
=f
U
D
r
D
l
d
r
S
f
√
gd
2/3
.
On the assumption that H/l ∼ U
D
/r
D
, deduce that the same model can be
applied for time varying storm flow provided the maximum rainfall intensity
satisfies r
S
f
√
gH, and show that this is always the case.
6.4 Suppose that there is a suspended sediment mean concentration c>0, and that
in the model
δεh
t
+∇.(hu) =r,
δF
2
δεu
t
+(u.∇)u
=−∇η −
|u|u
h
,
η =s +δh +δνa,
δε(hc)
t
+∇.(hcu) =γ(E−cD),
δνa
t
+∇.Q =−α(E −cD) +A,
s
t
=−A +U,
τ
e
=|u|u −β∇s,
we have α ∼ γ 1, ε, δ 1, E is an increasing function of u, and D is a
decreasing function of u. Show that, approximately, c = c(u) is an increasing
function of stream speed, and that the hillslope erosion equation is approxi-
mately
∂s
∂t
=U −∇.Q −
α
γ
∇.[hcu].
Deduce that the suspended load term acts as a stabilising, diffusive influence
on the hillslope evolution.
How do solutions behave if α γ 1?
6.5 In one space dimension (with x pointing downhill), a model for overland flow
and hillslope erosion takes the form
q
x
=r, s
t
+F
x
=U. (∗)
Assuming that F =F(q,S) and S =−s
x
, write the system in the form
A
s
q
t
+B
s
q
x
=c,
specifying the matrices A and B, and the vector c.
