Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

360 6 Landscape Evolution

It is a peculiarity of the Meyer-Peter/Müller law that A =0 to leading order, so that

the steady state is approximately neutrally linearly stable. Simpliﬁcation of (6.136)

now yields

−δ

1/2

∂Z

∂T

∂H

∂T



1/2

3/2

1/2

∂

∂Y



βH

1/2

∂H

∂Y



∂

∂Y

, (6.141)

with inessential error terms of O(δ

1/3

(6.141) reveals the essence of linear instability and its nonlinear development.

Linear instability is associated with the negative diffusion coefﬁcient of Z if A>0,

i.e.,

S<S

, (6.142)

using (6.20)

and (6.32). In dimensional terms, this suggests instability if the slope

is less than μ

, which occurs precisely at the shoreline. If the resulting rills are

able to grow to signiﬁcant depth, then the nonlinear evolution of H is described

approximately by

∂H

∂T



1/2

3/2

1/2

∂

∂Y



βH

1/2

∂H

∂Y



, (6.143)

and Z then follows from (6.136) by quadrature.

(6.143) is a degenerate nonlinear diffusion equation, about which a good deal is

known. The source term is suggestive (if S



> 0, i.e., on the (upper) convex portion

of the hillslope) of blow-up, and the possibility that H could reach ∞at a ﬁnite time.

The degenerate diffusion coefﬁcient is suggestive of solutions of compact support.

If such solutions develop, then the integral constraint (6.134) can be written in the

form



∞

−∞

3/2

dY =

2Lrx

1/2

. (6.144)

Note that this constraint is independent of Eq. (6.143), which is derived from sed-

iment conservation, whereas (6.144) is a condition of water mass ﬂow. More pre-

cisely, the right hand side is an upper bound for the left hand side, since there may

be a non-zero ﬂux arising from the outer solution.

Suitable boundary conditions for (6.143) follow from matching to an outer ﬁlm

ﬂow, where Y ∼ 1/δ

1/2

and H ∼δ

1/3

. Consequently, we require

H →0asY →±∞. (6.145)

A suitable initial condition is less easy to provide, other than stating that H is

initially small (since we suppose it arises from an instability of the steady state

H ∼δ

1/3

). The reason for this is that we have omitted an intermediate discussion

of the nonlinear stability of the steady state. The long time evolution of an arbi-

trary (small) perturbation to the steady state can be described by consideration of a

Meaning that they are non-zero only on ﬁnite interval(s).

6.6 Channel Formation 361

Fourier integral over normal modes of wave number k. The upshot of this is that the

emerging linear solution is a monochromatic oscillation whose wave number is that

with maximum growth rate, and this would serve as a suitable initial condition for

the resulting nonlinear equations in (6.131). However, to obtain an appropriate ini-

tial condition for (6.143), we really need to know how solutions to (6.131) behave.

In seeking solutions at larger amplitude, we are motivated by the fact that developed

river channels do attain depths on the order of a metre, and thus we implicitly assume

that the nonlinear equations (6.131) do not have bounded stable solutions for H .

6.6.1 Channel Solutions

Suppose the channel depth satisﬁes (6.143), with coefﬁcients of O(1).

Suppose ﬁrst that S



< 0 (a concave slope, linearly unstable if it is a steady state).

The nonlinear algebraic term in (6.143) is thus negative, and we can expect solutions

to decay towards zero.

This suggests that large channels are not viable, although

paradoxically the uniform ﬁlm state is unstable. The implication is that in this case,

ﬁnite amplitude rill solutions of (6.131) exist and are stable.

If S



> 0, then channels can grow. If we deﬁne

Y =



2β





1/2

ξ, T =



1/2

, (6.146)

then H satisﬁes

3/2



3/2



ξξ

, (6.147)

with the constraint



∞

−∞

3/2

dξ =

Q =





βS



1/2

Lrx. (6.148)

With this constraint, there is a unique steady state corresponding to a single isolated

channel,

3/2

cosξ. (6.149)

6.6.2 Bank Migration, Stability and Blow-up

The hallmark of nonlinear diffusion equations such as (6.147) is that we expect to

have solutions with compact support, and we expect the margins (where H =0) to

For constant uplift U and rainfall r and the Meyer-Peter/Müller transport law (6.139), this is not

true for the steady state slope, since then S =

+O(δ

1/3

). Nevertheless it is reasonable to suppose



=O(1), either because the base state is not in equilibrium, or because uplift and/or rainfall are

not uniform.

This is easy to show, by consideration of the time derivative of



∞

−∞

dY.

362 6 Landscape Evolution

move at ﬁnite rates. If H ≈a(ξ

−ξ)

near a margin ξ = ξ

, then a local balance

in (6.147) shows that either ν = 2(H is smooth) and

≈ 3a

1/2

(the margin ad-

vances) or ν = 2/3 and the margin is stationary (see also Question 6.12). Actually

this latter result is inconclusive, since if H ≈ a(ξ

−ξ)

2/3

+ b(ξ

− ξ)

4/3

+···,

then

≈

15b

1/2

, and can be zero, positive or negative. This appears to be the more

general result, and it also shows that great care needs to be taken in solving (6.147)

numerically.

Let us deﬁne

u =H

3/2

, (6.150)

so that

1/3

=u +u

ξξ

, (6.151)

with steady state solution

u =

cosξ. (6.152)

We write

u =

cosξ +V, (6.153)

and linearise the equation on the basis that V is small, so that

3cos

1/3

=V +V

ξξ

. (6.154)

If V is zero and analytic at the margins, then the margins are stationary at ±π/2, in

view of the above discussion on margin migration. Multiplying by V and integrat-

ing,

dτ



π/2

−π/2

cos

1/3

dξ =



π/2

−π/2



−V



dξ (6.155)

(since V =0at±π/2). Now the variational principle for the right hand side integral

as a functional of V tells us that it is maximised when V ∝cosξ , in which case the

right hand side is zero. V =cosξ is not an admissible solution to (6.155), since the

integral constraint (6.148) also implies that



π/2

−π/2

Vdξ=0, (6.156)

and therefore it follows that

dτ



π/2

−π/2

cos

1/3

dξ < 0. (6.157)

Equally one can show that all normal modes for V decay. This indicates that the

steady state is linearly stable. Numerical computations conﬁrm that the steady state

is indeed globally stable. Further discussion of the solutions of (6.147), and in par-

ticular of the issue of blow-up, is given in the notes (see also Question 6.13).

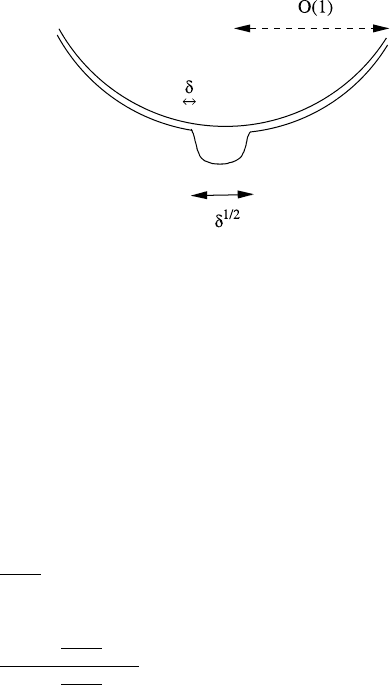
6.7 Channels and Hillslope Evolution 363

Fig. 6.5 Expected solution

structure for (6.158)

6.7 Channels and Hillslope Evolution

As the channels described by (6.143) evolve, a transverse ﬂow will develop on the

hillslope, causing erosion and thus subsidence. The effect of this on the hillslope is

that the assumption of a basic one-dimensional downhill slope becomes unrealistic,

and a channel will be ﬂanked on either side by different hillslopes. We now show

how this situation can be described.

We revert to the model (6.105), using the Meyer-Peter/Müller transport law:

∇.[qn]=r,

q =h

3/2

|∇η|

1/2

−δh

=U −∇.[f N],

n =−

∇η

|∇η |

=−(h +β)∇η +δβ∇h,

N =−



∇η −

δβ

(h+β)

∇h





∇η −

δβ

(h+β)

∇h



f =[τ

−τ

∗

]

3/2

(6.158)

Our key to the solution behaviour stems from how we expect channels and hillslope

to behave; this is shown in Fig. 6.5. We have already described channels, of width

O(δ

1/2

). On the hillslope, we now seek solutions in which η ∼O(1),butη depends

on both x and y (i.e., the gradient is not simply in the x direction).

On the hillslope, appropriate scales are η ∼1, h ∼ 1, q ∼1, and the approximate

model for η ≈ s and h is just (6.27), as before. In the channel, which we take to

be at y =0, we have h =H/δ

1/3

, q =Q/δ

1/3

, y = δ

1/2

Y , η =η

(x) +δZ (where

(x) = η(x,0)), t = δT , and the channel depth satisﬁes (6.143), and we suppose

H →0atY =±Y

It is clear that if the outer hillslope depends on y (and thus feeds water to the

channel), then ∇η must have a sharp jump between hillslope and channel, and in

order for this to occur, there must be a singular transition region near the channel

margin (i.e., the river bank). In this bank layer, we put

y =δ

1/2

+δζ, η =η

(x) +δZ, h ∼1,q∼1. (6.159)

364 6 Landscape Evolution

Again, we may linearise the geometry, and we obtain

n =−

(η



), N ≈



−η



(h +β)

−Z



, (6.160)

where

S =



2



1/2

,E=



2



(h +β)

−Z





1/2

. (6.161)

The effective shear stress is then

≈(h +β)E. (6.162)

At leading order, the water and sediment conservation equations are simply

∂

∂ζ





≈0,

∂

∂ζ





(h +β)

−Z



≈0,

(6.163)

which state that the water and sediment ﬂuxes are continuous across the bank. Thus

3/2

1/2

=K,



(h +β)

−Z



=−C, (6.164)

where K and C are constants (the water and sediment ﬂuxes to the channel). The

existence of a satisfactory bank transition layer relies on the solutions of (6.164)

being able to match both to the hillslope ﬁlm ﬂow and the deep channel ﬂow.

If the outer hillslope limits of ﬁlm thickness and normal slope are h

= h(x, 0)

and μ =

∂η(x,0)

∂y

> 0 (for y>0), then we require

→μ, h →h

as ζ →∞. (6.165)

The steady channel solution (6.149) is still applicable, and from this we ﬁnd that the

appropriate matching conditions to the channel are

3/2

∼−Aζ, Z

→0asζ →−∞. (6.166)

(Since h →∞as ζ →−∞,(6.163) implies Z

→ 0.) If

Q is the volume ﬂux in

the channel, then

A =



4βS

1/2

, (6.167)

where S

=|η



Let S

be the slope at the channel of the hillslope, i.e.,



+μ



1/2

; (6.168)

E here is unrelated to the dimensionless erosion rate used a long time ago in (6.16).

6.7 Channels and Hillslope Evolution 365

then as ζ →∞, E → S

, τ

→(h

+β)S

, and comparison of equations (6.164)

with the matching condition (6.165) then shows that

K =

3/2

1/2

,C=

f {(h

+β)S

}μ

. (6.169)

Equally, as ζ →−∞, S → S

, E → S

, thus τ

∼ S

h, f ∼ S

3/2

, h

3/2

∼

−Aζ , h

/h∼2/3ζ and Z

∼KS

1/2

3/2

; it follows from (6.166) that

2βS

1/2

=C. (6.170)

It now remains to see whether a connecting solution of (6.164) exists. Using the

deﬁnition of S in (6.161), we can solve (6.164)

to ﬁnd

=U(h) ≡

√





+4S



1/2



1/2

. (6.171)

U(h) is a monotonically decreasing function of h, with

U ∼

as h →0,

U ∼

1/2

3/2

as h →∞.

(6.172)

Next we deﬁne

L = Z

−

(h +β)

. (6.173)

We have the Meyer-Peter/Müller law f =[(h + β)E −τ

∗

]

3/2

, where E =[S

]

1/2

, and (6.164)

is simply fL= EC. This implies L>0, and simpliﬁcation

then shows that

h +β =

∗

2/3



1 +



1/3

)

1/2

. (6.174)

This deﬁnes h in terms of L as a monotonically decreasing function, with h →−β

as L →∞, and h ∼(

)

1/3

as L →0. Thus L(h) is a monotonically decreasing

positive function, with L(0) being ﬁnite and

L ∼

1/2

3/2

as h →∞. (6.175)

It now follows from (6.173) that h is given by the solution of the ordinary differ-

ential equation

(h +β)

=U(h)−L(h). (6.176)

The function U −L is positive and decreasing for small h, and as h →∞,(6.170),

(6.172) and (6.175) imply that U −L ∼−

2βA

3/2

. Since this is negative, it implies

366 6 Landscape Evolution

Fig. 6.6 A channel in an

evolving landscape

that there is a zero

of U −L and that U −L<0forh>h

. Consequently, the

solution of (6.176) takes h from ∞ (and speciﬁcally h

3/2

∼−Aζ )asζ →−∞to

as ζ →∞, as required. Thus the bank singular layer engineers the transition we

seek in adjusting the hillslope to the channel.

6.7.1 Hillslope Evolution

The analysis of the preceding section provides a series of recipes which relate the

hillslope to the channel. Now we show how this combination provides a way to

compute the long term evolution of the hillslope without having to resolve (compu-

tationally) the details of the bank and channel.

The situation we have in mind is shown in Fig. 6.6. Suppose that we know the

channel location, i.e., η

(x); then we also know S

. We can therefore solve (6.27)

for s ≈η and h, given zero ﬂux conditions on the adjoining ridges, and in this way

μ and h

are determined.

Equations (6.167) and (6.169) provide three prescriptions for A, K and C, and

then (6.170) determines an ordinary differential equation for S

.Ifwetakef =

[τ

−τ

∗

]

3/2

, τ

≈(h +β)S

, where (6.168)givesS

in terms of S

, then we have



2μ



+β)

3/2

−τ

∗

−h

3/2

1/2



. (6.177)

In addition the water ﬂux to the channel is just 2K (if we suppose that a symmet-

ric slope lies in y<0). Therefore the water ﬂux

Q in the channel satisﬁes



2μh

3/2

1/2

. (6.178)

(The prime denotes differentiation with respect to x.) A similar equation for the

sediment ﬂux in the channel is satisﬁed,



−Y

FdY=2C. Since F (rescaled) in

the channel is approximately QS

, it follows from this that (S



=2C, but in fact

this is already implied by (6.177) and (6.178).

Probably only one, but if there were more, then h

is taken as the largest zero.

6.7 Channels and Hillslope Evolution 367

Equations (6.177) and (6.178) provide two ordinary differential equations for

channel water ﬂux

Q and channel slope S

. Since S

=−η



, we therefore have

a second order differential equation for channel elevation η

, with boundary con-

ditions specifying its source (contiguous with the hillslope) and terminus. In gen-

eral, these equations must be solved numerically (see also Question 6.14). Note that



> 0, consistent with the basic assumption in the channel description.

6.7.2 Detachment Limited Erosion

One of the worrying features of Smith–Bretherton model and our discussion of it is

that channels form when S



> 0, i.e., the hillslope is convex, and indeed the resulting

channel long proﬁle is also convex. This is inconsistent with what we expect from

the linear stability results, and also in practice. Consulting (6.136), we can see that

the source term in the nonlinear diffusion equation for channel depth h,(6.143),

arises from the term

∂F

∂x

, and speciﬁcally from its S component, i.e.,

∂F

∂S



. Since

∂F

∂S

> 0, positivity of the source requires S



> 0.

This is odd, because we would expect sediment ﬂux to increase with distance

downstream irrespective of whether the slope is convex or concave. In fact, there is

something not quite right with the use of the sediment transport law in the form f ≈

qS, because it implies that there is a sediment ﬂux even if there is no sediment! The

resolution of this paradox lies in the formulation of the original sediment transport

model in the form (6.20). There we allowed for the existence of a non-zero thickness

a of the bedload layer. In order to pose a more physically realistic transport law, we

need to retain the dependence of sediment ﬂux on a, and therefore we modify our

deﬁnition of the sediment ﬂux from that in (6.21)tobe

=f N, (6.179)

where

f =a ˆv. (6.180)

Because of the speciﬁc inclusion of a, we see that ˆv is the mean bedload speed, and

evidently this will be in the direction of the mean effective stress, N. We expect that

ˆv will depend on ﬂow speed and slope, and indeed that it will be consistent with

measured transport rates.

Equally, we suppose the abrasion rate A in (6.20) must depend on a. Erosion or

mobilisation of an underlying rock or compacted sediment due to the rubbing of a

mobile overlying layer of thickness can be expected to decrease as a increases, and

to be speciﬁc, we will suppose that

A =

A[1 −a]

, (6.181)

368 6 Landscape Evolution

where

A will depend on the stress, and the (dimensionless) thickness at which bed

abrasion ceases can be taken to be a =1 by the choice of scale for a.

In order that

f give the Meyer-Peter/Müller result when a =1, we take

ˆv =[τ

−τ

∗

]

3/2

, (6.182)

and to be speciﬁc, we will suppose that

A =α ˆv, (6.183)

since the driving process for bedload transport and abrasion is the same. The dimen-

sionless parameter α is thus the ratio of abrasion rate to uplift rate.

Consulting (6.20), we see that in a channel, with s =η −δh −δνa, η =η

+δZ,

h =H/δ

1/3

, t =δ

7/6

T , f = F/δ

1/2

, τ

/δ

1/3

, and if we put A =

A/δ

1/2

, ˆv =

V/δ

1/2

, then

1/3

−νa

]−H

=δ

1/2

U −

1/3

νa

+∇.[F N]=

(6.184)

where

F =aV,

A =αV (1 −a), V =



−δ

2/3

∗



3/2

. (6.185)

At leading order in a channel, we thus have

A =∇.[F N]. (6.186)

The ﬁrst thing to do is to see whether this prescription for sediment transport can

be consistent with the observation that bedload transport depends only on bed stress.

Suppose that in a one-dimensional ﬂume, the ﬂow and depth are constant, so that

also V is constant. Then we have

=αV (1 −a), (6.187)

whence

a =1 −exp(−αx). (6.188)

This immediately identiﬁes two limiting régimes, transport limited and detachment

limited. The transport limited régime occurs when α  1. Then a → 1 rapidly,

and the sediment transport F ≈ V , which gives the Meyer-Peter/Müller result. If,

however, α  1, we have detachment limited transport, in which F ≈ αV x, and

transport is limited by the rate that sediment can be eroded from the underlying

regolith. Arguably, this is the more likely situation in mature mountainous terrain.

Let us now revisit the derivation of the deep channel equation, allowing for the

variable bedload density. In the channel, V ≈ QS, and thus

A ≈αQS(1 −a), and

This choice is distinct from our earlier assumption in (6.20), which was that U ∼A. By selecting

the scale for a to be the presumed value where abrasion ceases, we cannot guarantee A ∼U ,and

therefore A is not necessarily O(1).

6.7 Channels and Hillslope Evolution 369

F ≈ aQS. Using the linearised geometric description of N in (6.110), we ﬁnd that

(6.186) becomes

=α(1 −a)QS =

∂F

∂x

−

∂

∂Y



∂Z

∂Y



∂

∂Y



βF

∂H

∂Y



, (6.189)

while the water ﬂow equation is approximately

∂

∂Y



∂Z

∂Y



, (6.190)

and Q ≈H

3/2

1/2

We can use (6.190) and the deﬁnition of Q to write (6.189) in the form

αS −a



αS +S





=Sa

−



−

βH



, (6.191)

where D is the diffusion term we had before for H ,

D =

∂

∂Y



βH

1/2

∂H

∂Y



. (6.192)

Obviously it is no longer simple to solve this equation for a. If we suppose that

S and Q are known, then (6.191) is a hyperbolic equation for a. The characteristics

come into the channel from the bank and turn downstream. A reasonable estimate

for the solution follows from neglecting the term proportional to a

. In this case,

the solution satisfying a =0atx =x

a =



S(X)exp



−





α +







dX. (6.193)

There is a fundamental distinction between the solutions depending on whether

αQS +D ≶ 0. If αQS +D > 0, then a increases towards a saturation value. Since

we expect D < 0 (because of the steady solutions of (6.147)), this (transport limited)

case occurs if α is large enough. If α 1, then direct asymptotic solution of (6.191)

shows that a = 1 +O(1/α), thus S(1 −a) ≈



), and therefore

∂H

∂T

≈QS



+D, (6.194)

which is the same result as (6.143), and this is therefore the transport limiting chan-

nel equation.

If, on the other hand, α  1, then we can expect αQS + D < 0, and the ac-

tive bedload continues to increase, but is small: a ∼ α. No major simpliﬁcation of

(6.193) is possible, but we do have

∂H

∂T

=QS +O(α). (6.195)

Evolution of channel depth is on the longer time scale T ∼O(1/α), and the source

term is QS ≈H

3/2

and is independent of curvature. We might suppose that the

diffusive term is included in the O(α) term, and this is borne out by (6.193)ifwe