George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

PART IV Pulse Doppler Radar

244

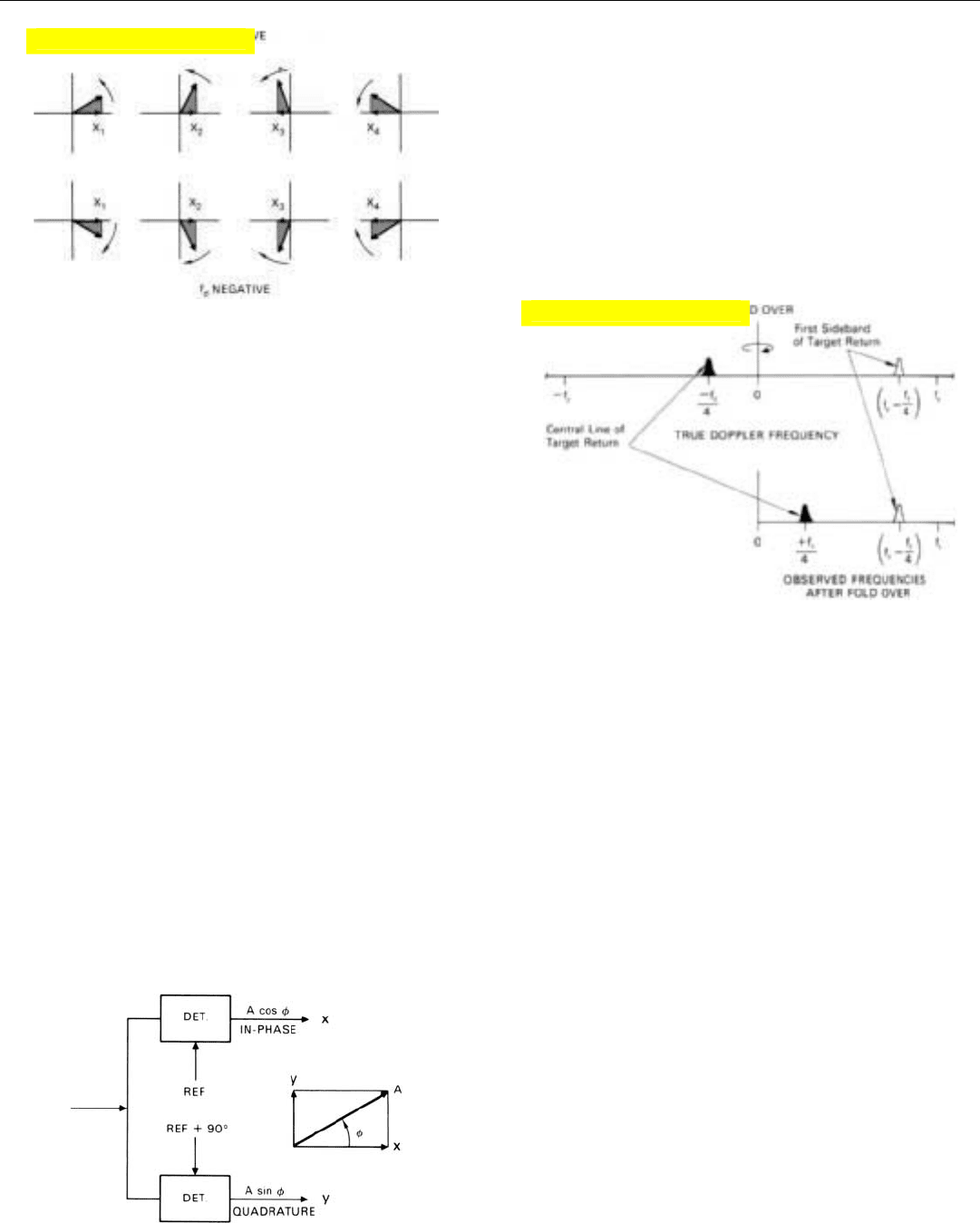
whether the phasor rotates clockwise or counterclockwise

(Fig. 21). On the basis of these projections alone, we have

no way of telling whether the target’s doppler frequency is

positive or negative. Indeed, in simple MTI radars, which

process only one component of the return, all doppler fre-

quencies are indicated as positive. The negative half of the

doppler spectrum is said to be “folded over” onto the posi-

tive half. Thus, a target whose doppler frequency is, say,

–

/4f

will also appear to have a doppler frequency of +

(Fig. 22).

The above limitations can be eliminated by simultane-

ously applying the IF output to a second synchronous

detector to which the same reference signal is applied, but

with a 90° phase lag.

Since the cosine of (φ – 90°) equals

the sine of φ, the output voltage of this detector is propor-

tional to the amplitude of the target return times the sine of

the phase angle, φ, relative to the unshifted reference.

output 2

= A sin φ

We can conveniently visualize this second output as the

projection of the phasor representation of the target return

onto the y axis, as in Fig. 23. Now, if the second detector’s

output (y) lags behind the first detector’s output (x), we

know that the phasor is rotating counterclockwise: the tar-

get’s doppler frequency is positive. On the other hand, if y

leads x, we know that the phasor is rotating clockwise: the

target’s doppler frequency is negative.

The x projection is called the in-phase or I component; the

y projection, the quadrature or Q component. Together, the

two projections describe the phasor completely. Their vec-

tor sum equals the length of the phasor (A).

22. If only one component of the return is processed, the negative

portion of the doppler spectrum will be folded over onto the

positive portion.

23. Two channel detector system. Reference frequency for quadra-

ture channel has 90

° phase lag.

4. To avoid imbalances, a single

detector and A/D converter

may instead be alternately

used for I and Q channels.

The sampling rate must then

be doubled.

21. Detector output for successive echoes. In-phase or quadrature

component alone is the same for both positive and negative

doppler frequencies.

Click for high-quality image

Their ratio,

together with their algebraic signs, unam-

biguously indicate the phase angle, φ; hence, both the rate

and the direction of the phasor’s rotation.

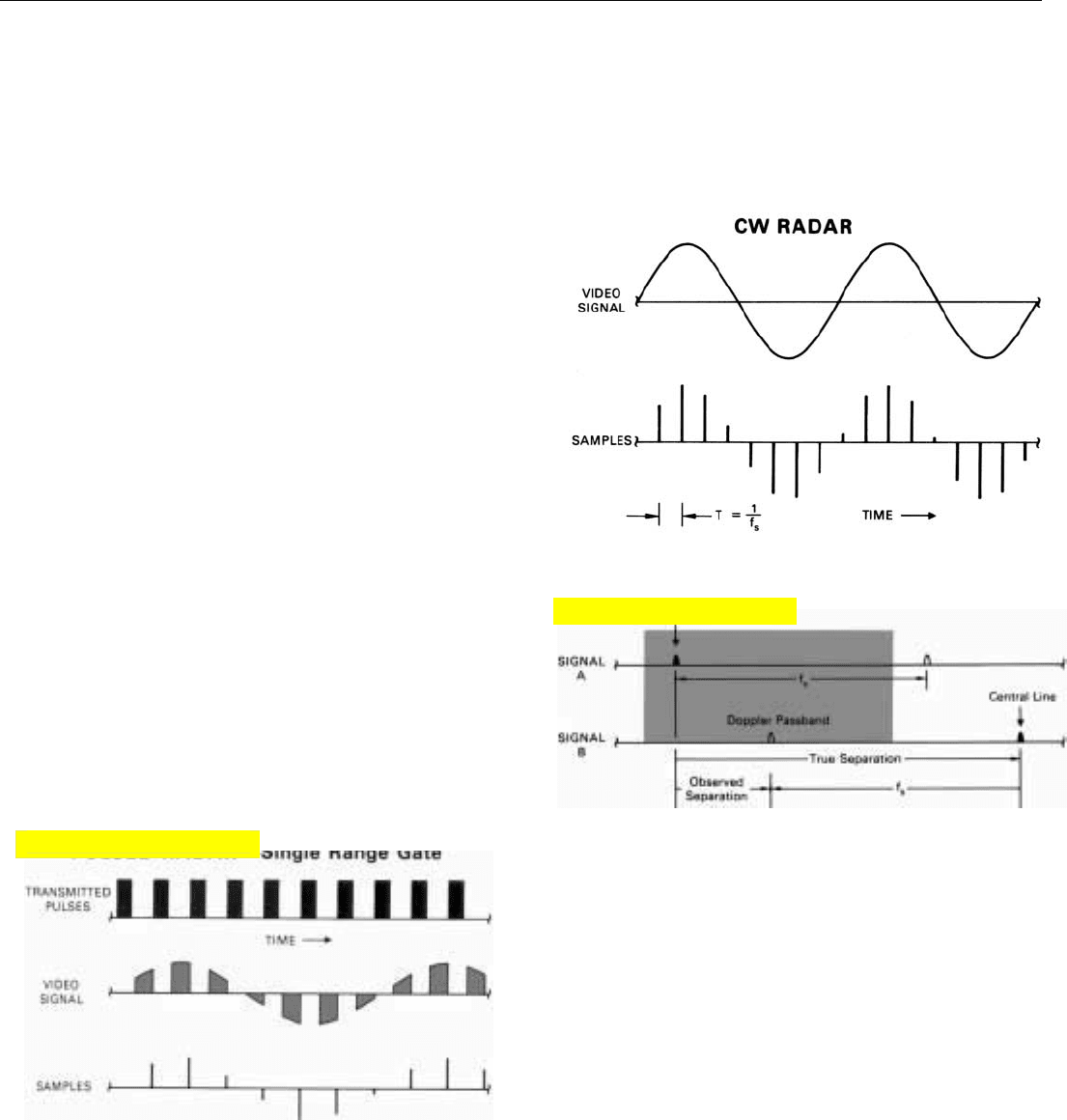
Sampling the Video Signals. So that the continuously

varying outputs of the I and Q detectors can be converted

to digital numbers, they must be sampled at short intervals

of time. Because the outputs may be rapidly varying, the

sampling rate must be precisely controlled to avoid intro-

ducing errors. Depending upon the design of the radar, the

rate may range anywhere from a few hundred thousand to

hundreds of millions of samples per second.

In a CW radar, the rate must at least equal the width of

the band of frequencies to be passed by the doppler filter

bank. If the rate is less than this, the sampling will intro-

duce frequency ambiguities. The reason is that sampling

converts the CW signal into a pulsed signal whose repeti-

tion frequency is the sampling rate (Fig. 24). The spectral

lines of a pulsed signal, of course, recur at intervals equal

to the repetition rate. Consequently, if two signals are

received whose true doppler frequencies differ by more

than the sampling rate, the observed difference in their fre-

quencies will be the true difference minus the sampling rate

(Fig. 25).

In a pulsed radar, sampling corresponds to the range gat-

ing performed in analog mechanizations. If only one sample

is taken during each interpulse period—as might be done if

the PRF were high and the duty factor close to 50 percent—

the radar is said to have a single range gate (Fig. 26).

CHAPTER 18 Sensing Doppler Frequencies

245

24. When a CW video signal is sampled, it is converted to a pulsed

signal whose PRF is the sampling rate, f

25. Doppler spectra of two CW signals after sampling when sampling

rate f

is less than signals’ true frequency separation.

5. Actually, the ratio is the tan-

gent of the phase angle; the

arctangent of the ratio is the

phase angle.

Obviously, the sampling rate in this case would be the PRF.

Where the equivalent of more than one range gate is

required, the sampling rate must equal the PRF times the

number of range gates. Each sample then represents the

return of a single pulse from a given range increment—or,

26. If only one sample is taken between transmitted pulses, the

radar has the equivalent of a single range gate. Note that the

samples are taken at the end of the sampling intervals.

Click for high-quality image

29. Functions performed by a digital filter during each successive

integration time, t

int

PART IV Pulse Doppler Radar

246

if range is ambiguous, from a number of range increments

separated by the unambiguous range, R

(Fig. 27).

27. If more than one sample is taken between transmitted pulses, suc-

cessive samples represent returns from different ranges (or sets of

ranges if range is ambiguous).

28.

At regular intervals, I and Q video signals are momentarily sam-

pled. Samples are held long enough to be converted to numbers.

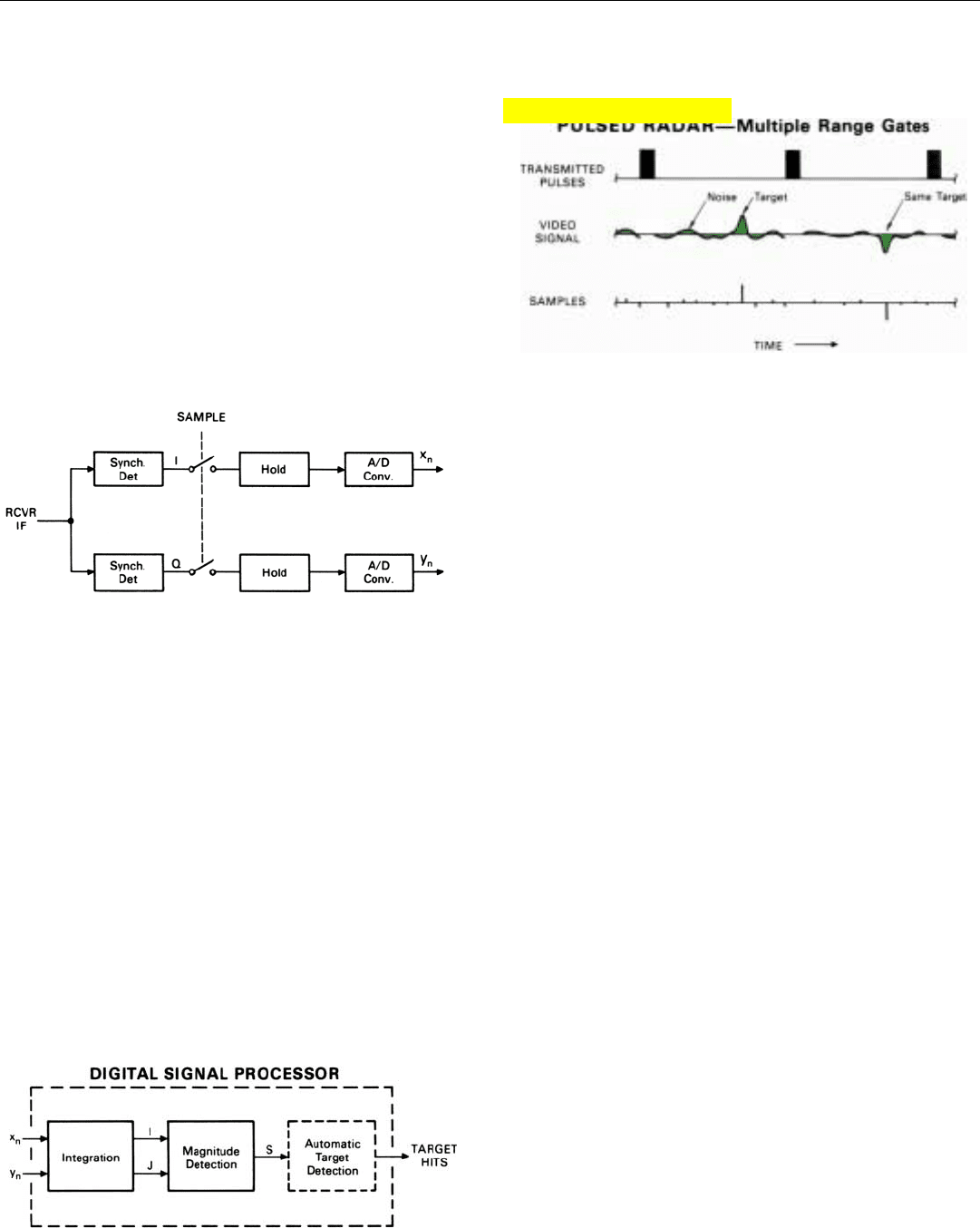
In either case, the sampling is generally performed with

“sample-and-hold” circuits. Separate circuits are provided

for the outputs of both the I and the Q detector (Fig. 28).

At precisely the required intervals, these circuits sense the

instantaneous values of the output voltages. They hold the

samples long enough for them to be converted to digital

numbers, then dump them, and the process repeats.

Analog-to-Digital Conversion. Exactly how this conver-

sion is done depends upon the length of time between sam-

ples, the maximum rate at which the voltage being sampled

may change, the required conversion accuracy, cost consid-

erations, and so on.

In essence, though, most mechanizations are much the

same. The A/D converter compares the voltage of each sam-

ple it receives with a succession of progressively higher

voltages of precisely known value. When the closest of

these is found, the converter outputs a binary number equal

to the known voltage. The panel on the facing page illus-

trates in general how this process might be performed.

Separate converters (or converter channels) are provided

for the I and Q samples. The continuous stream of binary

numbers emerging from the converter(s) is supplied to the

computer which forms the doppler filters.

Forming the Filters. During each successive integration

time, t

int

, the computer mathematically forms a separate

bank of doppler filters for every range gate.

Each filter in the bank for a given range gate receives as

inputs the same set of numbers (x

, y

) from the A/D con-

verter (Fig. 29). If return is being received from a target,

each pair of numbers constitutes the x and y components of

one sample of a signal whose amplitude corresponds to the

Click for high-quality image

CHAPTER 18 Sensing Doppler Frequencies

247

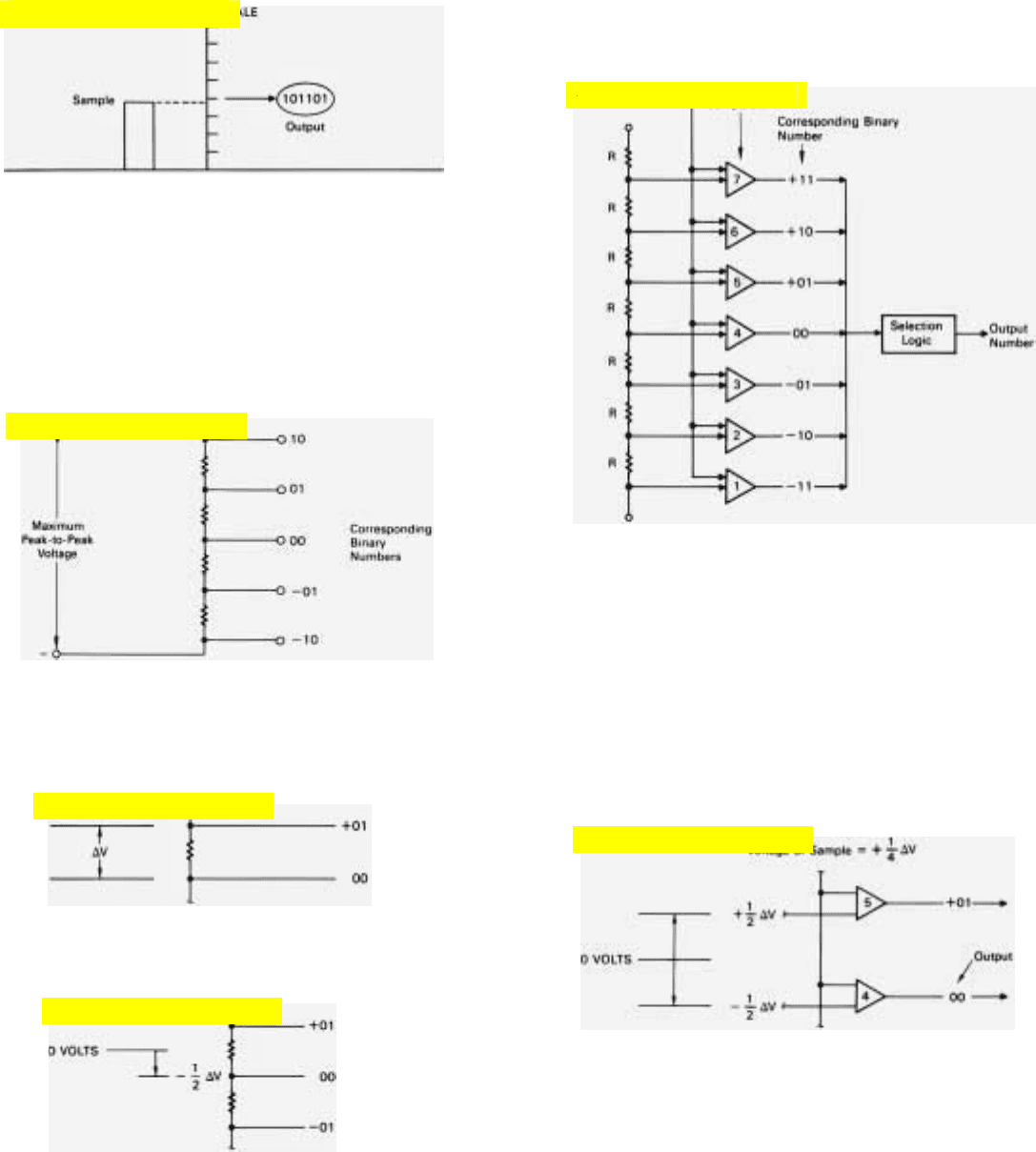
HOW AN A/D CONVERTER WORKS

WHAT IT DOES. In essence, an analog-to-digital converter compares each

sample of the signal that is to be digitized with a known scale of incrementally

increasing voltage.

It then outputs a binary number corresponding to the voltage step the sample

comes closest to equaling. To give an idea of how these functions might be

performed, the operation of a rudimentary two-digit-plus-sign converter is

outlined below.

THE VOLTAGE SCALE. This may be obtained by applying an extremely

stable voltage equal to the maximum possible peak-to-peak excursion of the

samples across a chain of precision resistors (voltage divider).

The voltage at each tap of this divider corresponds to one of the succession

of binary numbers to which the samples may be converted. The difference in

voltage from tap to tap, ∆V, corresponds to the value of the least significant

digit of these numbers—in this example, binary 1.

So, the numbers output by the converter will be correctly rounded off, the

taps are offset toward the negative end of the divider by half the intertap volt-

age, ∆V.

As a result, the voltages of all of the taps are half an increment less

positive than the positions of the taps would imply. The voltage of the

central tap, for instance, is not O but 

/2∆V.

COMPARING THE VOLTAGES. A bank of comparator circuits compares

the voltage of the sample that is to be digitized with the voltage of each tap.

Any one comparator produces an output only if the sample is more

positive than the tap to which the comparator is connected. For example,

if the voltage of the sample were 

/4∆V, an output would be produced

by Comparator 4 but not by Comparator 5.

SELECTION LOGIC. Each time a voltage sample is applied to the

converter, a logic circuit identifies the highest numbered comparator from

which an output is produced and outputs the binary number corresponding

to this tap. For instance, in the above example where the sample produced

an output from Comparator 4

but not from Comparator 5, the sample would be assumed to lie

somewhere in the range from 

/2∆V to 

/2∆V, and a zero would

be output.

Click for high-quality image

PART IV Pulse Doppler Radar

248

power of the target return and whose frequency is the tar-

get’s doppler frequency. The job of the filter is to integrate

these numbers in such a way that if the doppler frequency

is the same as the filter’s frequency, the sum will be large,

but otherwise it will not.

As will be explained in detail in the next chapter, filter

projects successive x and y components onto a coordinate

system (i, j) that rotates at the frequency the filter is tuned

to and sums the i and j projections separately. At the end of

the integration period, the magnitude of the integrated sig-

nal is computed by vectorially adding the two sums. To

detect targets automatically, the vector sum may be applied

to a threshold detector.

The series of computations (algorithm) which must be

performed to accomplish the integration and compute the

magnitude of the vector sum is called the discrete Fourier

transform (DFT).

Although the arithmetic is simple, the

required volume of computing can be enormous. Moreover,

to keep up with the flood of incoming data, the computing

must be done at exceptionally high speeds. By suitably

organizing the computations, however, the volume can be

slashed. The procedure commonly employed is called the

fast Fourier transform.

Providing Adequate Dynamic Range

As noted in earlier chapters, the relative amplitudes of

the returns received from different sources and different

ranges may vary enormously. Echoes from large short-range

targets may be as much as a billion times stronger than the

echoes of small distant targets, and ground return may be

many times stronger than the strongest target echoes. While

the problem may be alleviated by suitably varying the sys-

tem’s gain with time, it cannot be avoided because often

both strong and weak returns are received simultaneously.

The system must not only be able to handle signals of max-

imum strength, but provide a wide enough range of output

levels at any one time so that small differences in output

due to simultaneously received echoes from small distant

targets can be detected. The solution, of course, is to pro-

vide adequate dynamic range.

By dynamic range is meant the spread between (1) the

minimum incremental change in the amplitude of the input

to a circuit or system which will produce a discernible

change in output and (2) the maximum peak-to-peak

amplitude which the input can have without saturating the

output. That is, without reaching a point where the output

no longer responds to a further increase in input. Beyond

6. It’s called “discrete” because

it applies to samples of a

continuous function taken at

discrete intervals of time.

this point, the output becomes a distorted representation of

the input.

Providing adequate dynamic range is an important con-

sideration in the design of the receiving and signal process-

ing system of any radar. But in the case of a radar which

must sense doppler frequencies it is crucial. For if the

dynamic range is inadequate, not only may weak signals be

masked by strong signals, but spurious signals will be creat-

ed. These signals, whose frequencies may be quite different

from those of the received signals, may appear falsely as

echoes from other targets or interfere with the detection of

true targets.

Source of the Spurious Signals. The spurious signals are

of two types: harmonics and cross modulation products.

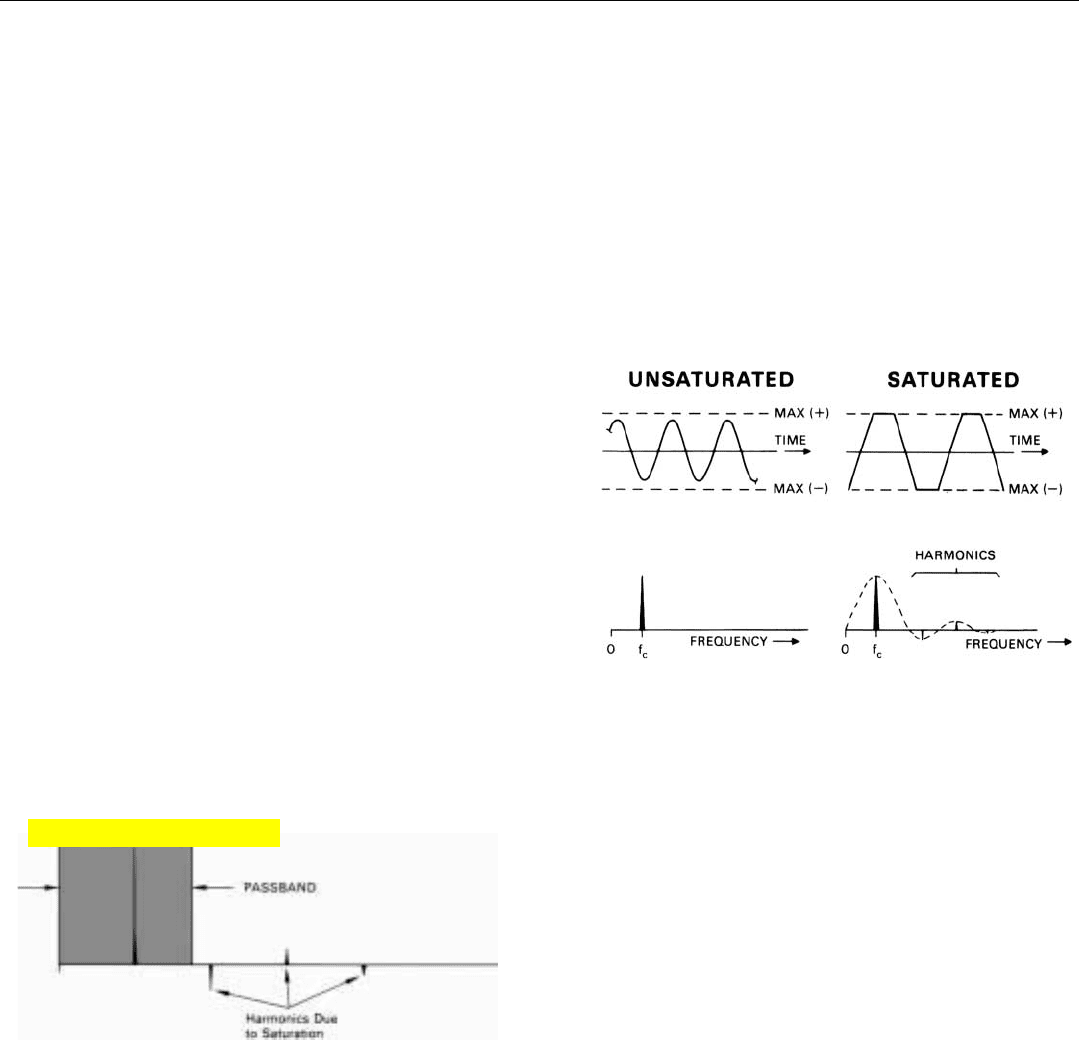
Harmonics are signals whose frequencies are multiples of

another signal’s frequency. That harmonics are created when

a system’s output is limited by saturation can be demon-

strated simply by lopping off the top and bottom of a sine

wave (Fig. 30).

The result is a nearly square wave. As we saw in Chap.

17, such a wave is made up of a series of sine waves whose

frequencies are multiples of the frequency of the square

wave.

If a system’s passband is narrow enough, the harmonics

may lie outside the passband and so be rejected (Fig. 31).

Otherwise, they may cause problems.

Cross modulation is the modulation of one signal by

another. It is produced if the sum of two or more signals of

different frequency is limited by saturation. The products

of cross modulation are sidebands. They, of course, occur

both above and below the frequencies of the modulated

signals.

Consequently, if the frequencies of the saturating signals

are closely spaced, a great many cross modulation products

will be passed by a system regardless of the width of its

passband.

CHAPTER 18 Sensing Doppler Frequencies

249

30. Harmonics are created when a signal’s peak amplitude is lim-

ited by saturation.

31. If passband is narrow enough, harmonics due to saturation

may be eliminated.

Click for high-quality image

7. For a triangular wave shape,

the rms value is approximate-

ly (1 +





) x LSD.

33.

Ideally, you would like the quantization noise to be one-tenth or

less of the system noise, and the saturation limit to be sufficiently

far above the system noise to accommodate the strong signals.

PART IV Pulse Doppler Radar

250

Avoiding Saturation. The creation of harmonics and

cross modulation products may be avoided simply by

avoiding saturation.

Toward this end, in designing a signal processing system,

the average signal level is usually kept as low as possible

without risking the loss of weak signals in the locally gener-

ated noise. Enough dynamic range is then provided to pre-

vent strong signals from saturating the system. Generally,

this approach leads to a tradeoff between saturation, on the

one hand, and low-level noise on the other.

Dealing with Quantization Noise. If the signal processor

is digital, the problem of low-level noise is exacerbated by

the presence of so-called quantization noise. It is the

inevitable result of representing signal amplitudes which

are continuously variable, with digital numbers which are

graduated in finite steps—quanta.

The effect is illustrated for a linearly changing signal in

Fig. 32. After being digitized, the signal actually consists of

the sum of two signals: (1) a quantized replica of the origi-

nal analog signal and (2) a triangular error wave having a

peak amplitude equal to half the value of the least signifi-

cant digit (LSD).

If the original signal is comprised of periodic samples of

the return from a given range, a simple triangular error

wave is generally not produced. For successive samples are

about as likely to fall at one point as another between the

steps of the A/D converter’s reference voltage. Consequently,

this undesirable byproduct of digitization is more or less

random and so is customarily categorized as noise.

Quantization noise in both the A/D converter and the

processor puts a lower limit on the signal levels that can be

handled by a system. A common figure of merit for an A/D’s

dynamic range is the ratio of (1) the maximum peak signal

voltage the A/D can handle to (2) the rms value of the

quantization error voltage.

To avoid degrading signal-to-noise ratios, you would like

the quantization noise to contribute only negligibly to the

overall system noise. For that, the level of the incoming sig-

nals must be set high enough that the level of the noise

accompanying the signals is substantially higher than the

quantization noise—ideally, on the order of 10 times higher

(Fig. 33).

To prevent saturation by strong signals, then, the dynam-

ic range must be correspondingly increased. This may

require increasing the number of digits in the numbers

used to represent the signals or handling the processing in a

more clever way or both.

32. If a gradually changing voltage is represented by digital num-

bers, the error due to quantization has a triangular shape and

a peak amplitude equal to half the value of the least signifi-

cant digit (LSD).

Click for high-quality image

Summary

To sort out the radar return from various objects accord-

ing to doppler frequency, the receiver output is applied to a

bank of narrowband filters. If sorting by range is also

desired, a separate bank is provided for each range incre-

ment. The width of the passband of a narrowband filter is

primarily determined by the filter’s integration time but is

increased by losses. So that return will not be lost when a

target straddles two filters, the passbands are made to over-

lap. So that only one line of a target’s spectrum will fall

within the band of frequencies bracketed by the bank, the

passband of the bank is made no greater than the PRF.

The filters may be either analog or digital. For analog fil-

tering, the radar return is translated to a relatively low

intermediate radio frequency. Each filter typically uses one

or more quartz crystals. Its response to an incoming signal

is analogous to that of a pendulum’s response to a succes-

sion of impulses.

For digital filtering, the IF output of the receiver is trans-

lated to video frequencies by applying it to a pair of syn-

chronous detectors, along with a reference signal whose fre-

quency corresponds to that of the transmitter. The outputs

of the detectors represent the in-phase (I) and quadrature

(Q) components of the return. Quadrature components are

needed to preserve the sense of the doppler frequencies.

The outputs of the synchronous detectors are sampled at

a precisely controlled rate. In a pulsed radar, sampling cor-

responds to the range gating of an analog processor. The

sampling rate equals the PRF times the number of range

gates desired.

Each sample is converted to a binary number by com-

paring its voltage with a succession of progressively higher

voltages of precisely known value. The numbers are then

supplied to a special purpose computer, which implements

the filters.

In the case of both analog and digital filters, targets may

be detected automatically by applying the filter outputs to

threshold detectors.

CHAPTER 18 Sensing Doppler Frequencies

251

253

How Digital Filters Work

n the preceding chapter we saw how, for digital filtering,

the radar returns are translated to video frequencies by a

pair of synchronous detectors and sampled at precisely

timed intervals. And we learned how the samples are

converted to digital numbers. We were told that the numbers

are then supplied to a computer (signal processor), which

“forms” a separate bank of doppler filters for each sampling

interval (range gate).

But little was said about the way in

which the filters are formed.

In this chapter, we will learn how that is done. After briefly

reviewing what the stream of numbers supplied to the com-

puter represents, we will derive the simple set of equations

(algorithm) which the filter must repeatedly compute to form

a filter—the discrete Fourier transform—and see how the

required mathematical operations may be organized. Finally,

we will briefly consider what can be done to reduce the side-

lobes which invariably occur on either side of a filter’s pass-

band.

The organization of a complete filter bank and the inge-

nious approach taken to minimizing the otherwise staggering

computing load (the fast Fourier transform) are covered in the

next chapter.

Inputs to the Filter

Before delving into the details of the digital filter’s opera-

tion, it will be well to have a good physical picture of what the

digitized samples that are the inputs to the filter actually rep-

resent. We can gain a picture of this sort quite easily by view-

ing the output of one of a pulsed radar’s two synchronous

detectors on a range trace.

1. Depending on the radar’s

PRF, the returns passed by

any one range gate may all

come from the same range

increment or they may come

from many ambiguous range

increments separated by R

PART IV Pulse Doppler Radar

254

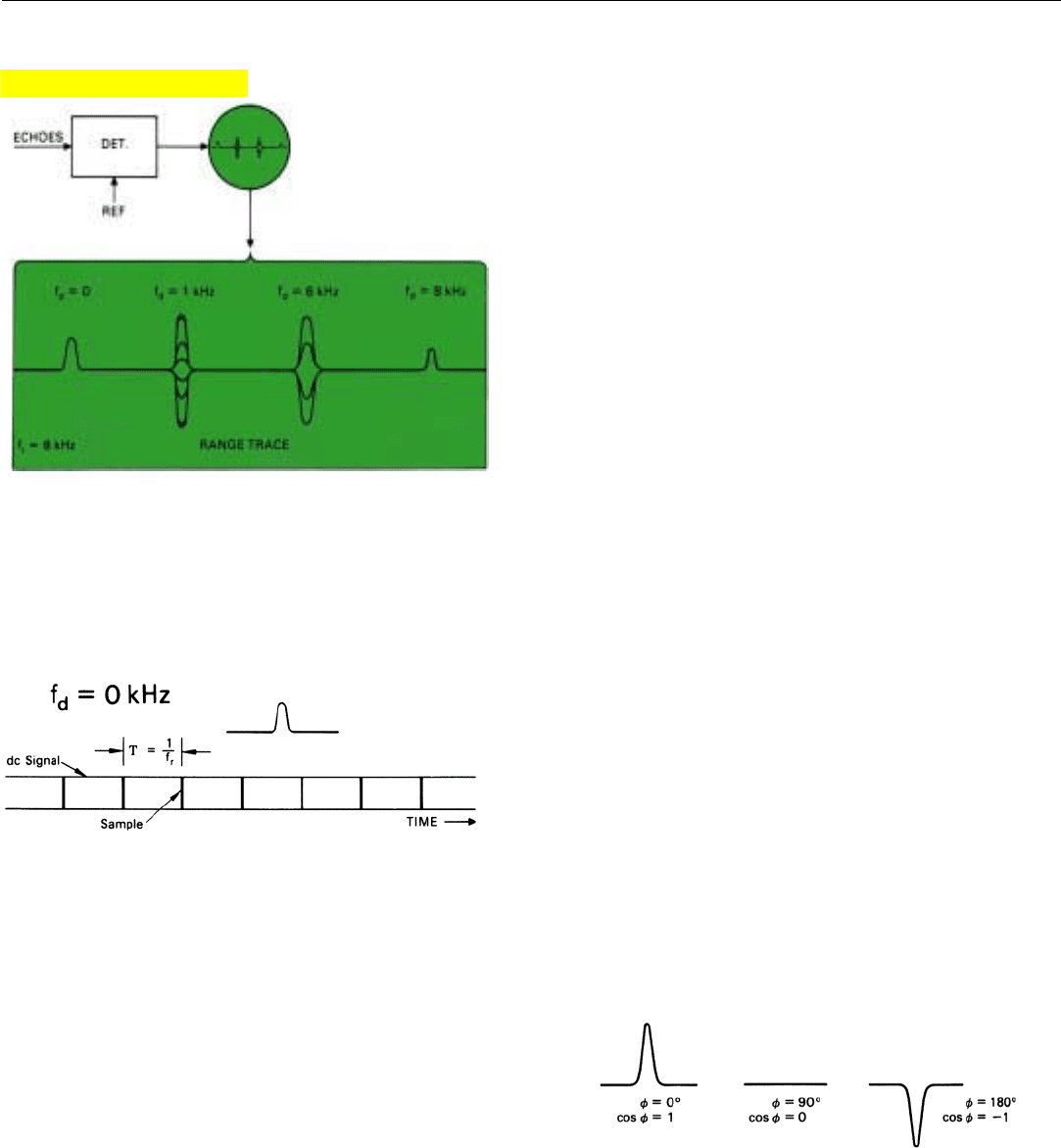
Detector Output Displayed on a Range Trace. Let us

suppose that the output of the in-phase (I) detector is sup-

plied to the vertical deflection circuit of an oscilloscope on

which is displayed a horizontal range trace. The I output,

you’ll recall, equals A cos φ, where A is the amplitude and φ

is the radio-frequency phase of the target return relative to

the reference signal supplied to the detector. The radar’s

PRF, we’ll say, is 8 kilohertz. Echoes are being received from

four targets. Their doppler frequencies are 0, 1, 6, and 8

kilohertz. So that we can isolate the echoes of each target

on the range trace, the targets have been positioned at pro-

gressively greater ranges (Fig. 1). To isolate the effects of the

frequency differences, we will assume that the amplitudes

of the received echoes are all the same.

Despite this similarity, the “pips” which the four targets

produce are all quite different. Not only do they vary in

height, but some fluctuate and others do not. To appreciate

why this is so, you must bear in mind that the height of a

target pip drawn on the oscilloscope during any one range

sweep (interpulse period) corresponds to the detector out-

put produced by a single target echo. Since in this case the

period of even the highest doppler frequency is a great deal

longer than the width of a radar pulse, each pip is essential-

ly a sample taken at a single point in a cycle of the target’s

doppler frequency.

For the target having zero doppler frequency, the height

of successive pips is constant (Fig. 2). The reason is fairly

obvious. Since the target echoes have the same frequency as

the reference signal, their phase, relative to it, does not

change from one echo to the next. The detector output for

the range increment in which this target resides is a pulsed

dc voltage. As was explained in the last chapter, the ampli-

tude of this voltage may lie anywhere between zero and

plus or minus A, depending upon the phase (φ) of the tar-

get echoes (Fig. 3).

1. Output of a single-channel synchronous detector displayed on

a range trace. Echoes of equal amplitude are being received

from four targets having different doppler frequencies.

2. Detector output for target with zero doppler frequency has

constant amplitude.

3. Depending on the echo’s radio frequency phase, the amplitude of

detector output for zero doppler frequency may be anywhere

between +1 and –1 times echo’s amplitude.

One of the reasons for providing both I and Q channels,

of course, is to eliminate this variability. Since the output of

the I detector equals A cos φ and the output of the Q detec-

tor equals A sin φ, the magnitude of the vector sum of the

two outputs for all values of φ equals A.

Click for high-quality image