Голдаев С.В., Ляликов Б.А. Основы математического моделирования в теплотехнике

Подождите немного. Документ загружается.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

⎪

⎩

⎪

⎨

⎧

=++

2222121020

1212111010

0202101000

cababab

(2.13)

Вычисляя коэффициенты этой системы по формулам (2.11), где

i = 0, 1, 2, 3, 4, 5, получаем:

()

∑∑

∑

====

===

====

.226,335)()10/(,674,234)(10/

,42,206)(,596,2410/

,509,1410/

,153,910/

,538,610/,6

223

2112

201102

100100

ipiipi

cTccTc

ccTb

Tbb

Tbbb

μμ

Замечание. Чтобы избежать громоздких расчетов, табличные значения

температур были уменьшены в 1000 раз. Такой прием нормирования приме-

няется часто, например, при определении лучистого теплового потока по за-

кону Стефана – Больцмана, когда температуры газа, достигающие значений

3000 К, приходится возводить в четвертую степень [27-30].

Как видно, все коэффициенты b

при k+l = const равны между собой, что

сокращает объем вычислений.

Система уравнений (2.13) запишется в виде:

⎪

⎩

⎪

⎨

⎧

=++

.226,335596,24509,14153,9

,674,234509,14153,9538,6

,42,206153,9538,66

210

aaa

(2.14)

Определяем неизвестные по правилу Крамера [20], [36]:

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

,,,

211202210121102

210212120122110

22212

12111

02010

211200221001201102

211210201201221100

222120

121110

020100

bbcbcbcbb

bbccbbbbc

bbc

bbbbbbbbb

bbb

−−

−++

−−

−++

===

(2.15)

211002100120110

210102010121100

22120

11110

00100

212002210020102

2112102012022100

22220

12110

02000

bcbcbbbbc

bcbbcbcbb

cbb

bcbbbcbcb

bcb

−−

−++

−−

−++

Вычисляя определители, находим значения параметров эмпирической

формулы: a

= 26,48, a

= 11,37, a

= -2,94. Таким образом, искомая аппрок-

симация функции, заданной таблично, имеет вид:

(

)

(

)

.10/94,210/37,1148,26

TTc

−+=

Оценку достоверности этой интерполяционной формулы получим путем

вычисления относительных погрешностей в заданных точках молярных теп-

лоемкостей, т.е. найдем значения

)(

)()

(

)(

ipip

δμ

−

T, K

273 573 873 1273

1573 1973

кДж/(кмоль⋅К)

29, 278 31, 836 34, 206 35, 919 36,756 37, 720

кДж/(кмоль⋅К)

29, 373 32, 044 34, 184 36, 213 37,115 37, 49

δμ

0, 3 0, 6 0.06 0, 8 0, 95 0, 6

Как упоминалось выше, с целью повышения точности аппроксимирую-

щей функции используются полиномы высокой степени.

Пример 2.4 В опыте получены следующие данные, характеризующие

связь давления насыщения аммиака с температурой:

, K

273 278 283 288 293

, МПа 0,419 0,504 0,602 0,714 0,841

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

С помощью метода наименьших квадратов требуется выразить зависи-

мость ps = f(Ts) в виде:

210 ssss

TaTaTaap +++=

(2.16)

В данном случае имеем m = 3, n = 4, а система уравнений (2.10) запишет-

ся следующим образом:

⎪

⎩

⎪

⎨

⎧

=+++

3333232131030

2323222121020

1313212111010

0303202101000

cabababab

(2.17)

Решим эту систему методом Гаусса. Для исключения a

из второго,

третьего и четвертого уравнений прибавляем к ним первое, умноженное со-

ответственно на (–b

), (–b

0/b

). Получаем равносильную сис-

тему уравнений вида

⎪

⎩

⎪

⎨

⎧

=++

=+++

31333232131

21323222121

11313212111

0303202101000

cagagag

caeaeae

cadadad

cabababab

(2.18)

где

.,,

,,,

030

331

020

221

010

111

3003

3333

3002

3232

3001

3131

2003

2323

2002

2222

2001

2121

1003

1313

1002

1212

1001

1111

−=−=−=

(2.19)

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Теперь из последних двух уравнений исключаем a1. Для этого умножаем

второе уравнение последовательно на (–e

) и (–g

) и складываем с

третьим и четвертым уравнениями. Получаем:

⎪

⎩

⎪

⎨

⎧

=++

=+++

32333232

22323222

11313212111

0303202101000

caiai

cahah

cadadad

cabababab

(2.20)

где

1131

3132

1121

2122

3113

3333

3112

3232

2113

2323

2112

2222

−=−=

(2.21)

Наконец, исключаем a

из четвертого уравнения, умножая предыдущее на

(-i

) и складывая с ним:

⎪

⎩

⎪

⎨

⎧

=++

=+++

33333

22323222

11313212111

0303202101000

cah

cahah

cadadad

cabababab

(

2.21)

где

2232

3233

3223

3333

ih −=−=

(2.22)

На этом заканчивается прямой ход метода Гаусса.

Замечание. В процессе исключения неизвестных неоднократно выполня-

лись операции деления на коэффициенты b

и т.д. Поэтому они должны

быть отличными от нуля; в противном случае необходимо соответственным

образом переставить уравнения системы. Такая процедура должна быть пре-

дусмотрена в вычислительном алгоритме при его реализации на ЭВМ.

Обратный ход начинается с решения четвертого уравнения системы

(2.21):

33333

hca

Используя это значение, можно найти a

из третьего уравнения, а затем a

из второго и a

из первого.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Аналогично организуется вычислительный алгоритм для линейной сис-

темы с произвольным числом уравнений.

Возвращаясь к примеру 2.4, вычисляем коэффициенты этой системы по

формулам (2.11), где i = 0, 1, 2, 3, 4, получаем:

()

() ()

()

∑

∑∑

====

=======

========

.94,75)()10/(,65,26)()10/(

,36,9)(10/,29,3)(

,29,91310/,91,32110/

,63,259210/,54,113)10/(

,07,4010/,15,1410/,5

332

222

3223

312213

30211203

201102

100100

isiisi

isi

pTcpTc

pTcpc

TbbTbbb

TbTbbbb

TbbbTbbb

Реализуя метод Гаусса, находим по формулам (2.18), (2.20), (2.22) значе-

ния соответствующих коэффициентов:

,301,1,306,0,054,0,448,14

,801,0,402,3,801,0

,6,0,142,0,025,0

31211133

22322322

3113211211

====

cccg

egee

gdedd

.10091,1,107296,2,100808,1,1003,1

,10768,4,10657,2,10056,2,1068,2

−−−−

⋅=⋅=⋅=⋅−=

⋅=⋅=⋅=⋅=

chcc

iihh

Осуществляя обратный ход, подставляем найденные значения коэффици-

ентов в (2.21) и находим требуемые неизвестные:

=0,4, a

= -3,105, a

= 10,13, a

= -12, 21.

Следовательно, аппроксимационная зависимость (2.15) имеет вид:

.104,010105,31013,021,12

ssss

TTTp

−−

⋅+⋅−+−=

Ниже представлены файлы с программой, с исходными данными и ре-

зультатами решения системы линейных алгебраических уравнений методом

Гаусса.

program Gauss;

uses Uchism2;

var a,c : matr; b,x,g : vector; n : integer;

begin

assign(finp,'c:\tp55\bor\metod\mynew\mod\primer\dgauss.dat');

reset(finp);

assign(fout,'c:\tp55\bor\metod\mynew\mod\primer\rgauss.dat');

rewrite(fout); readln(finp,n); { Ввод ранга матрицы}

for I:=1 to N do for J:=1 to N do

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

read(finp,A[I,J]); readln(finp);{ Ввод матрицы }

for I:=1 to N do read(finp,b[i]); {Ввод вектора свободных

членов}

Gauss(n,a,b,x,g,c);

writeln(fout,'':10,'Вектор решения системы'); writeln(fout,'');

for i:=1 to n do write(fout,x[i]:9:3);

writeln(fout,''); writeln(' Программа закончила работу ...');

readln; close(finp); close(fout);

end.

Исходные данные

6.000 6.538 9.153

6.538 9.153 14.509

9.153 14.509 24.596

206.420 234.674 335.226

*** Вектор решения системы уравнений ***

26.495 11.370 -2.938

Пример 2.5. При построении на ЭВМ ректификационного процесса для

бинарной смеси (спирт- вода) необходимо перевести зависимость Y = f(X)

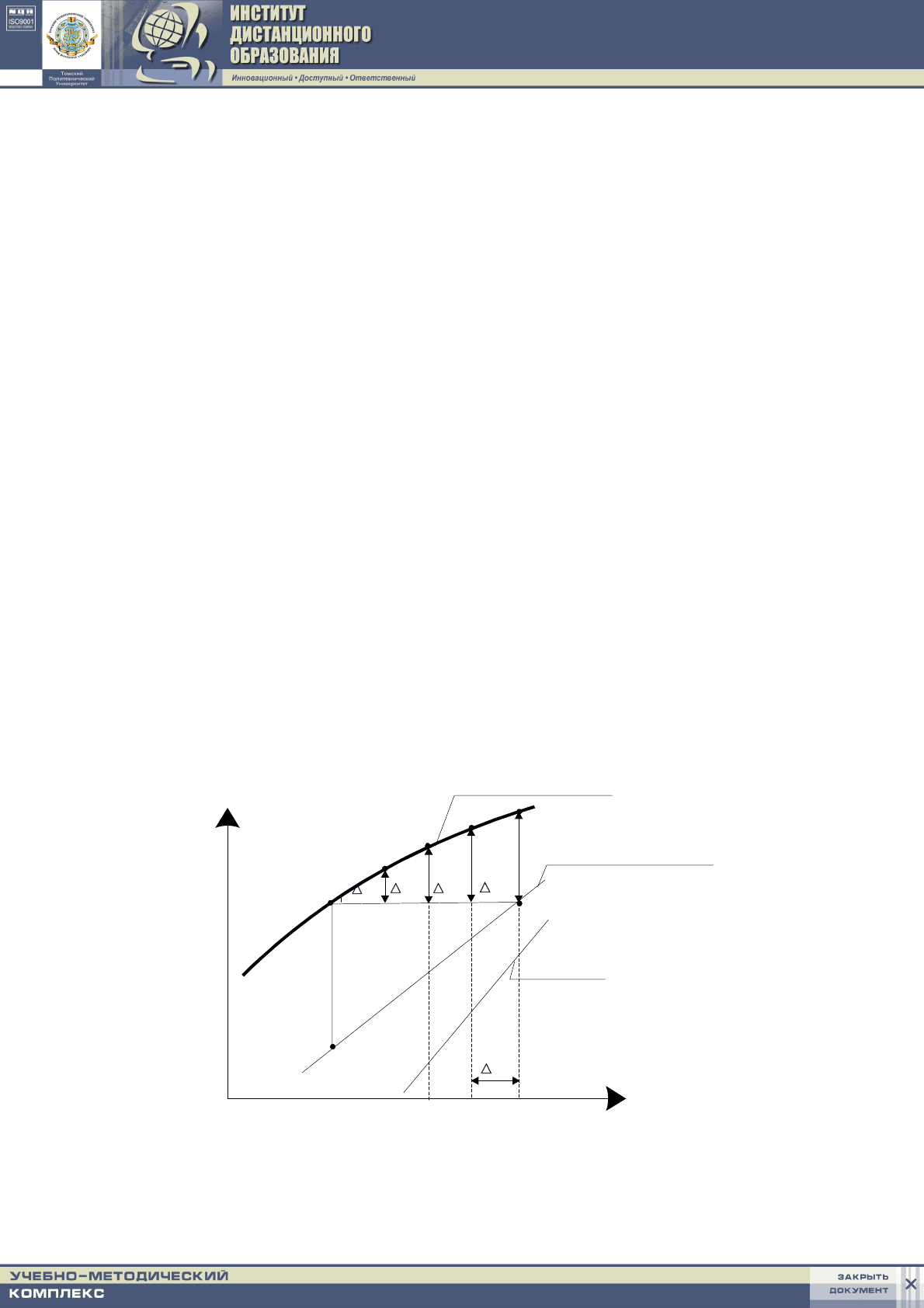
из табличной в аналитическую форму. На рис.2.8 показан укрупненный

фрагмент диаграммы равновесия, который помогает представить стадию мо-

делирования этого процесса для одной ступени [39].

Y=f (x)

Диагональ

Рабочая диагональ

Кривая равновесия

рл

кр

рл

кр

рл

(

)

Рис.2.2. Иллюстрация к построению ректификационного процесса.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Осуществим эту процедуру с применением метода наименьших квадра-

тов. Допустим, что координаты точки 1 заданы или определены из предыду-

щих расчетов. При построении линии 1-2 необходимо определить координа-

ты по X (так как Y

= const) точки 2 программным путем. При ручном

способе построения координата этой точки определяется проектировщиком

визуально при пересечении двух линий - кривой равновесия и горизонталь-

ной линии, исходящей из точки 1. На ЭВМ визуальное фиксирование точки,

образующейся при пересечении двух линий, возможно при использовании

графического редактора либо системы автоматизированного проектирования

(САПР). В данном примере рассматривается возм

ожность математического

моделирования процесса на основе аналитических расчетов координат точки

Алгоритм построения горизонтальной линии 1-2, т. е., в конечном ито-

ге, нахождение координаты X

, сводится к следующему итеративному циклу:

1.По величине абсциссы рабочей линии Х

точки 1 определяем значение ор-

динаты кривой равновесия Y

кр (с использованием процедур Appr и Yap).

2.Производим сравнение ординат кривой равновесия и рабочей линии:

ΔY

= Y

1кр

- Y

1рл

3.Если Y

кр

> Y

рл

, если ΔY

> ε (заданная степень точности), то значение X

рл

уменьшается на величину шага

X, и итерационный процесс продолжается,

иначе цикл по поиску координаты Х

кр

точки 2 прекращается с фиксацией

усредненного значения X

на последнем шаге.

Для построения точки 3 необходимо определить значение ординаты Y

3рл

которая находится из аналитического выражения рабочей линии по известному

значению X

2кр

Описанный алгоритм реализован в виде программы, листинг которой ,

исходные данные и результаты решения примера 2.5 представлены ниже.

program grappr;

uses uchism2;

var xxx1,yyy1 : mac16; {Массивы табличных данных аппроксими-

руемой зависимости}

begin

assign(finp,’c:\tp55\st\G6A54\dint1.dat’);

reset(finp);

assign(fout,’c:\tp55\st\G6A54\rint1.dat’);

rewrite(fout);

readln(finp,H); {Считывание количества точек в табличной зависимо-

сти}

for i:=1 to h do read(finp,xxx1[i]); { Считывание массивов табличных}

for i:=1 to h do read(finp,yyy1[i]); аргументов и функций}

Appr(H,E1,Xxx1,Yyy1,MM,Na,E,Z); {Обращение к процедуре аппрок-

симации}

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

writeln(fout,’’);

writeln(fout,’Полином аппроксимации кривой равновесия:’);

writeln(fout,’’);

write(fout,’ Y= ‘,Z[1]:9:3); {Вывод аппроксимирующего полинома}

for I:=2 to Na do

if (I=4) or (I=8) or (I=12) then

begin

if Z[i]>=0 then

write(fout,’ + ‘);

writeln(fout,Z[I]:10:3,’*X^’,I-1:2)

end

else

begin

if Z[i] >=0 then

write(fout,’ + ‘);

write(fout,Z[I]:10:3,’*X^’,I-1:2);

end;

writeln(fout,’’);

yap(0.9,z,q); {Расчет по аппроксимирующей функции для заданного

аргумента}

writeln(fout,’Для Х = 0.9 у = ‘, q:6:3);

Close(finp);

Close(Fout);

end.

Исходные данные

0 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

0 0.332 0.442 0.531 0.576 0.614 0.654 0.699 0.753 0.818 0.898 1.0

Полином аппроксимации кривой равновесия:

Y= 0.001 + 10.045

X - 90.169

+ 451.967

+1231.025

+ 1515.852

+ 529.552

- 4232.465

+5463.671

- 2969.596

+ 456.013

+ 97.155

Для Х = 0.9; Y = 0.898

3. МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

В ряде случаев анализа различных задач теплотехники [28-31] возникает

необходимость решения нелинейных уравнений вида

()

0,...,,

ppxF

(3.1)

где F(x) – некоторая непрерывная функция, p

, p

, - параметры.

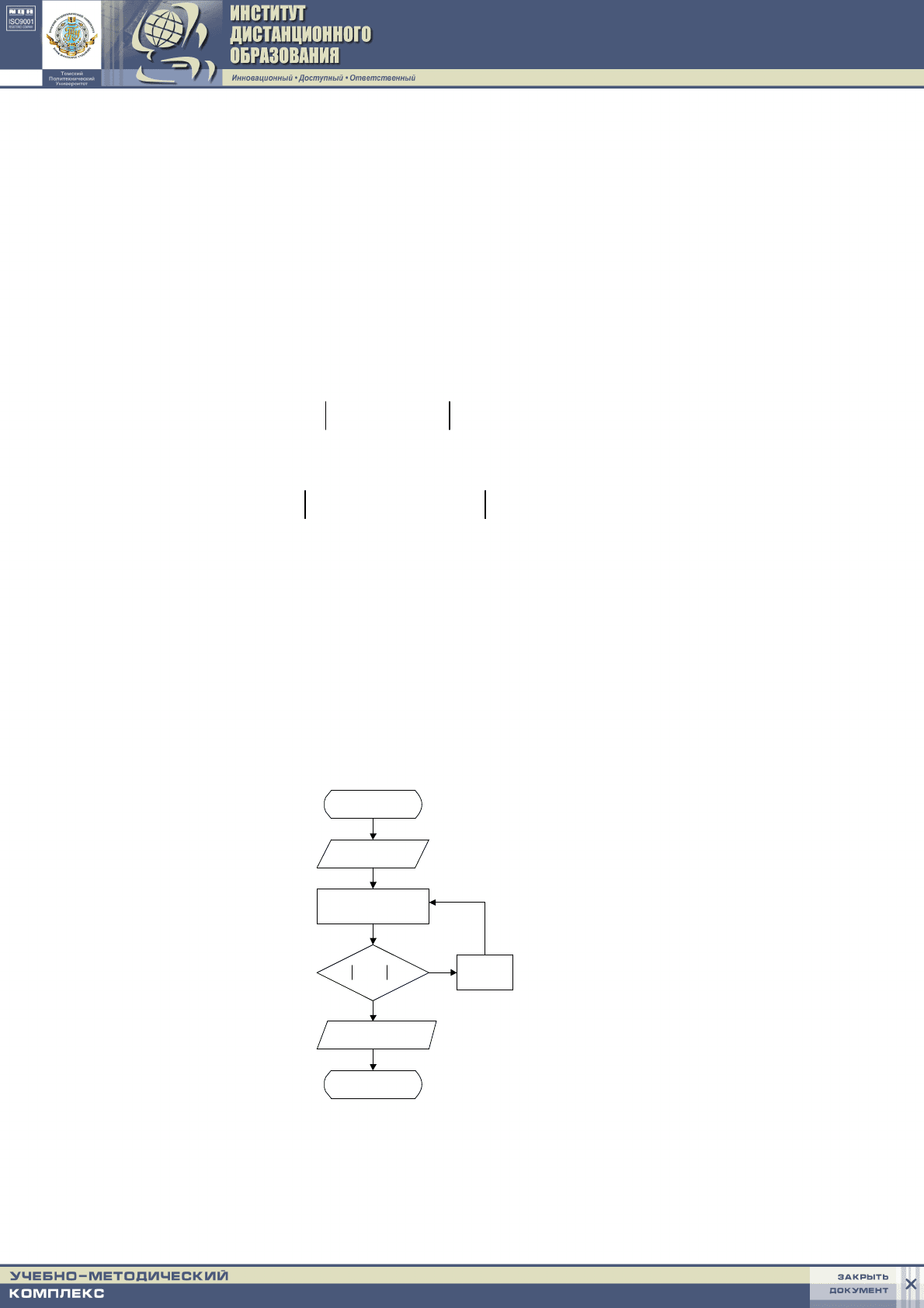
Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Разработано несколько приближенных алгоритмов решения такого типа

уравнений, которые относятся к итерационным [18], [20-23], [32], [36].

В методе простой итерации исходное уравнение (3.1) приводится к виду

()

,...,,

ppxfx =

(3.2)

Вначале графически или подбором находится нулевое (грубое) значение

корня x = с

, а затем оно уточняется путем последовательного вычисления

()

...),2,1(,,...,,

211

ippcfc

(3.3)

до тех пор, пока отличие последующего приближения от предыдущего не

превысит заданной погрешности ε, т.е.

()

<−

+ iii

ccc /

(3.4)

Описанный процесс сходится в случае, когда

()

1/,...,,

<dxppcdf

(3.5)

Если это условие не выполняется, то уравнение (3.2) преобразовывают

подходящим образом, например, переходя к обратной функции.

В тех вариантах, когда функция y = f(x) очень громоздкая, процедуру

схождения процесса проверяют практически, по критерию (3.4). Итерацион-

ный процесс может осуществляться колебательным образом, в течение кото-

рого значения x

приближаются к искомому корню то «сверху», то «снизу».

На рис.3.1 представлена блок-схема процесса решения нелинейного урав-

нения (3.2) этим методом.

Рис.3.1 Блок-схема метода

простой итерации

x-c

< ε

Начало

Ввод с

, ε

(c)

Вывод

Конец

Голдаев С.В., Ляликов Б.А. Основы математического моделирования

в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.

Здесь c – начальное приближение корня, а в дальнейшем – результат пре -

дыдущей итерации, x – значение корня после каждой итерации. В данном ал-

горитме предполагается, что итерационный процесс сходится. Если такой

уверенности нет, то необходимо ограничить число итераций или ввести про-

межуточную печать в цикле.

Листинг программы, составленной по описанному алгоритму, воспроиз-

веден ниже

program itera;

uses crt;

var x,x1,e:real; m,n,i:integer;

function f(x:real):real;

begin f:=5*(1-exp(-x)); end;

procedure iter (var x,e:real;

m:integer);

begin for i:=1 to m do begin

x1:=x; x:=f(x); if abs((x-x1)/x1)<e then exit;

if i=m then writeln ('iteratsi use')

end;

begin clrscr; repeat write(‘x,e,m: ‘); readln(x,e,m);

iter(x,e,m); writeln(‘x=’,x:6:4); until readkey = #27;

end.

После трансляции программы необходимо задать: начальное приближе-

ние, погрешность нахождения корня и ограничение на количество итераций.

При использовании метода хорд необходимо знать отрезок [a, b], на кото-

ром функция F(x, p

,…) меняет знак (Рис.3.2).

Рис.3.2 Иллюстрация метода хорд

y = F(x)