Голдаев С.В., Ляликов Б.А. Основы математического моделирования в теплотехнике
Подождите немного. Документ загружается.


Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
51
Получим разностное решение сформулированной задачи. Заменим произ-
водные в уравнении и граничном условии (6.3) по формулам численного
дифференцирования из гл.4:
(
)
ninzzhihzz
fkfi
≤
≤
−
=
+= 0,/,
.
Для внутренних узлов z
i
(1< i ≤ n-1), имеем:
(
)
0
2
1
2
11
2
11
=−
−
+
+
−
−+−+
i
ii
i
iii
u
h
uu
z
h
uuu
.
(6.5)
Граничное условие при z = z
k
аппроксимируем со вторым порядком по 3-
х точечной формуле [23]:
,
0 f
uu =
(
)
.0
2
43
:
21
=
+
−
=
−−
h
uuu
zz
nnn
k
(6.6)
В рассматриваемом примере z
f
= 1, z
k
= 2. Разбиваем этот отрезок на пять
частей, т.е. принимаем n = 5, тогда h = 0,2; z
1
=1,2: z
2
=1,4; z
3
=1,6; z
4
=1,8. За-
писываем последовательно (6.5) для i = 1, 2, 3 и 4, а (6.6) – для n = 5. После
простых преобразований получаем следующую систему линейных уравне-
ний:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
+=
+=
+=
+=
+=
,
,
,
,
,
39584
37564
25443
13322
01201
uauau
uauau
uauau
uauau
uauau
(6.7)
где
.4/1,4/3,463,0
2
2/1
,517,0
2
2/1
,460,0
2
2/1
,521,0
2
2/1
,455,0
2
2/1
,455,0
2
2/1
,449,0
2
2/1
,531,0
2
2/1
98
2
4
7
2
4
6
2
3
5
2
3
4
2
2
3
2
2
2
2
1
1
2
1
0
===
+
−
==
+
+
=
=
+
−
==
+
+
==
+
−
=
=
+
+
==
+
−
==
+
+
=
aa
h
zh
a
h
zh
a
h
zh
a
h
zh
a
h
zh
a
h
zh
a
h
zh
a
h
zh
a
Используя метод Гаусса, описанный в гл. 2, преобразуем (6.7) к следую-
щему виду:
()()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
−−=
+=
+=
+=
+=
./
,
,
,
,
608090705
3705604
2504403
1
0
33
0
22
01201
aaaau
uauau
uauau
uauau
uauau
(6.8)
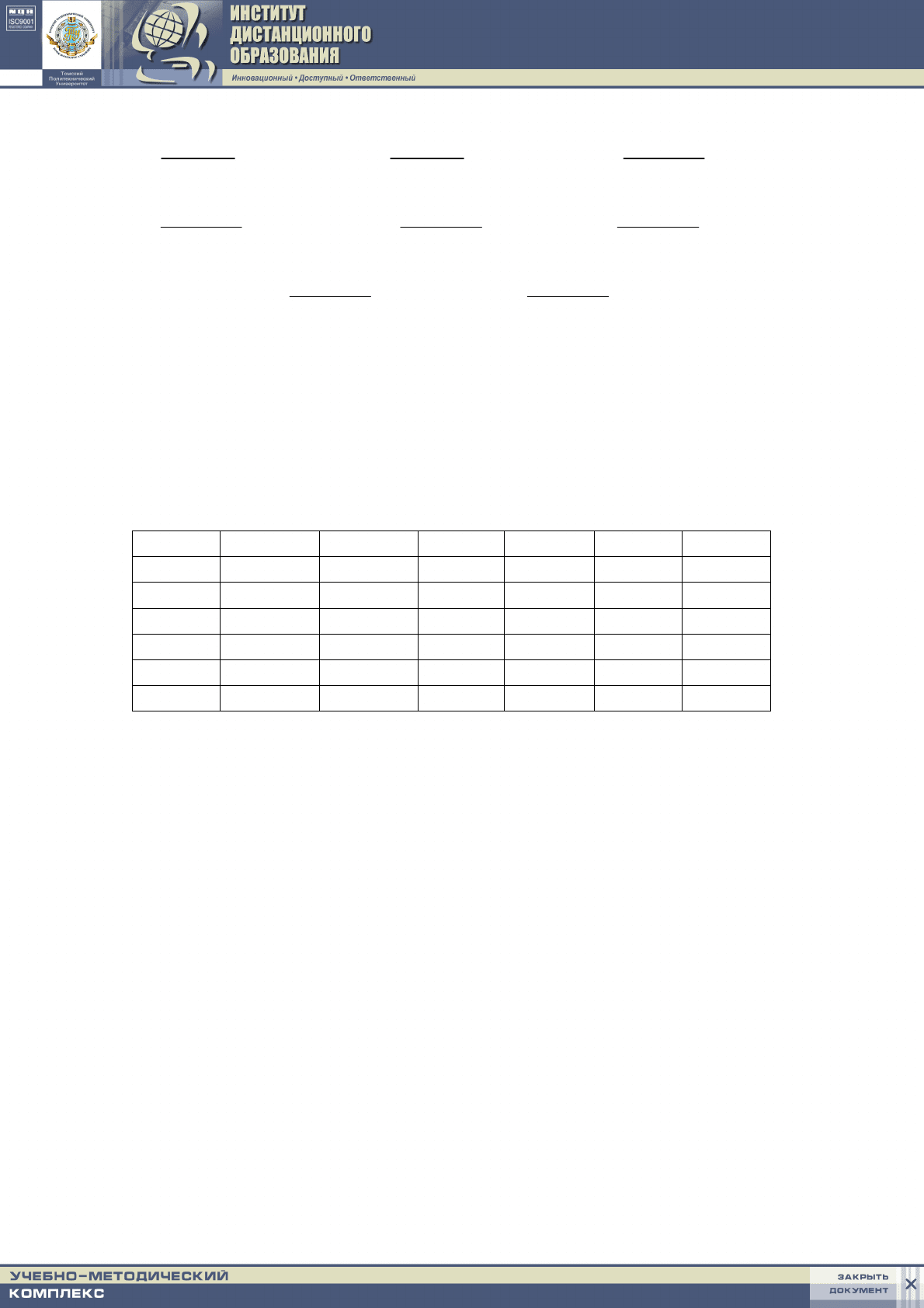
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
52
Здесь
.5618,0
1
,9268,0
1
,3017,1
1
,80,0
1
,6818,1
1
,7629,0
1
,6973,2
1
,6926,0
1
940
950
90
940
8
80
740
507
70
740
6
60
520
530
50
520
4
40
30
013
30
30
2
20
=
−
==
−
=
=
−
==
−
==
−
=
=
−
==
−
==
−
=
aa
aa
a
aa
a
a
aa
aa
a
aa
a
a
aa
aa
a
aa
a
a
aa
uaa
a
aa
a
a
Осуществляя обратный ход, получаем значения безразмерных температур
в точках 0, 1, 2, 3, 4, 5 (табл. 6.1, нижняя строка). Для определения погрешно-
сти численного интегрирования был проведен расчет по формуле (6.4) с ис-
пользованием необходимых величин функций Бесселя, заимствованных из
задачника [49]. Результаты помещены в этой же таблице. Сравнение точных
и приближенных величин u показывает их хорошее соответствие.
Таблица 6.1
z
1,0 1,2 1,4 1,6 1,8 2,0
I
0
(z)
1,266 1,394 1,553 1,750 1,990 2,280
I
1
(z)
0,566 0,715 0,886 1,085 1,317 1,591
K
0
(z)
0,421 0,318 0,244 0,188 0,146 0,114
K
1
(z)
0,602 0,435 0,320 0,241 0,183 0,140
u
a
10 8,276 7,150 6,424 6,031 5,910
u
10 8,270 7,112 6,3744 5,971 5,837
В рассмотренном ниже примере о решении стационарной задачи тепло-
проводности для плоской стенки с объемным источником тепловыделения
будет использован модифицированный метод Гаусса (метод прогонки) реше-
ния системы линейных уравнений, возникающей при переходе к разностному
аналогу краевой задачи.
Пример 6.2. Плоская стенка толщиной δ = 0,015м и высотой h =1,5 м име-
ет внутреннее тепловыделение q
v
= 107 Вт/м3 . Коэффициент теплопровод-
ности материала λ = 10 Вт/м
0
С. Стенка омывается рабочими средами с пара-
метрами: t
l,1
= 180
0
C, α
1
= 130 Вт/м
2
0
С,
t
l,2
= 130
0
C, α
2
= 85 Вт/м
2
0
С. Требу-
ется рассчитать: теплоту, рассеиваемую боковыми поверхностями Q1 (Вт/м),
Q
2
(Вт/м); координату максимальной температуры (x
m
) и максимальную тем-
пературу (t
m
); температуры поверхностей стенок t
1
и t
2
.
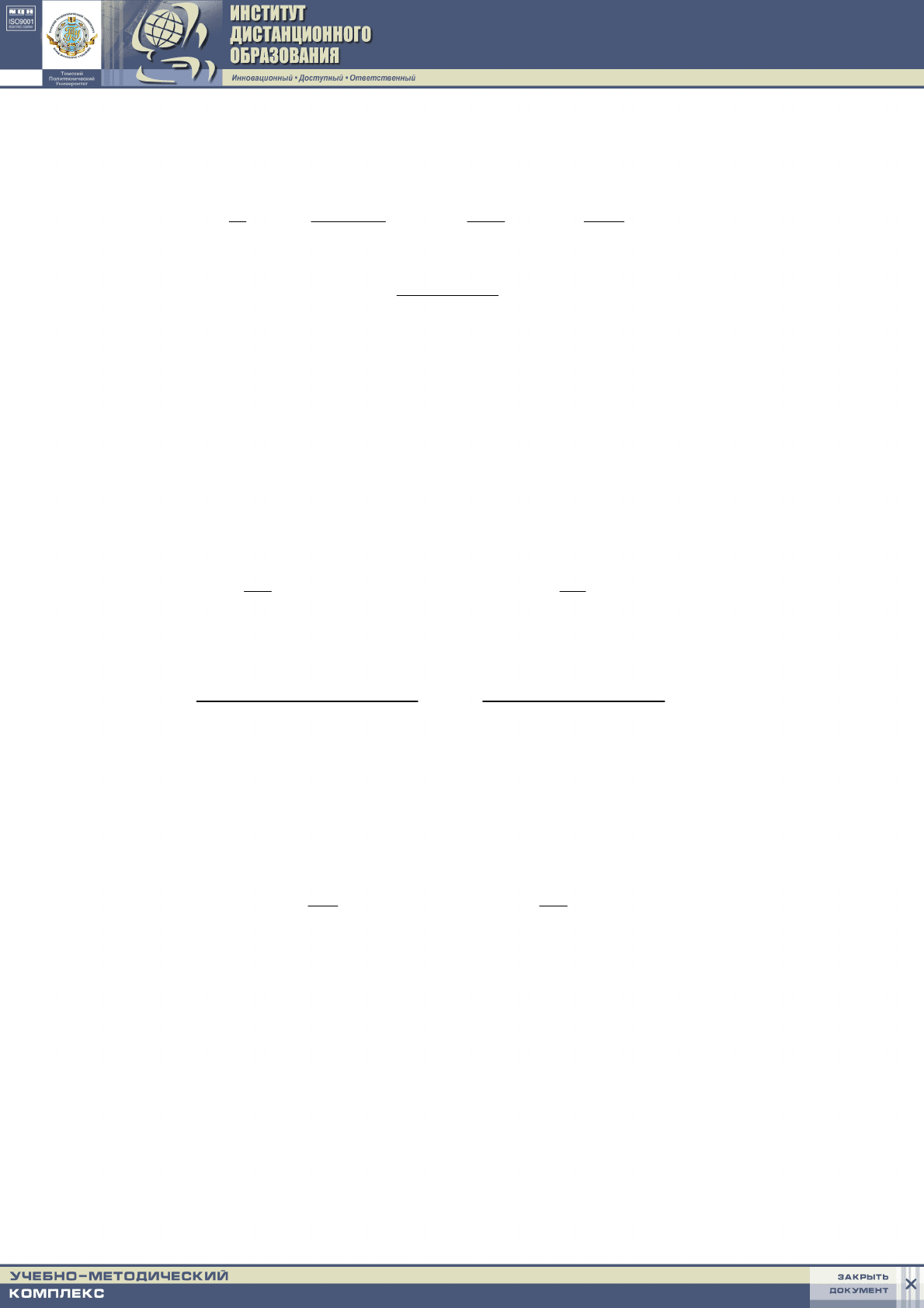
Решение. Математическая постановка задачи включает уравнение те-
плопроводности с источником тепловыделения и граничные условия 3-го ро-
да, моделирующие данный режим охлаждения стенки [28], [50]:
,0//
22
=+
λ
v
qdxtd
(6.9)
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
53
()
(
)
(
)
(
)
2,21,1
//:,//:0
ll
ttdxdtxttdxdtx −
−
=
=
−==
λ
α
δ
λ
α
Для удобства проведения количественного анализа перейдем к безраз-
мерным переменным, определяемым следующим образом:
()
,
,,,,
1,2,
2
2
2
1
1
1,2,
1,
ll
v
ll
l
tt
q
Po
BiBi
tt
tt
u
x
z
−
=
==
−
−
==
λ
δ
λ
δα
λ
δα
δ
(6.10)
где Bi , Po – критерии Био и Померанцева.
Краевая задача (6.9) примет вид:
()
.01/:1,/:0
,/
21
22
=++===
−=
uBidzduzuBidzduz
Podzud
(6.11)
Вначале получим аналитическое решение сформулированной задачи, ко-
торое будет использовано в дальнейшем для тестирования численного реше-
ния.
Интегрируя дважды уравнение (6.11), имеем:
.
2
,
2
z
PoCzDuCzPo
dz
du
−+=+−=
(6.12)
Определяя постоянные C и D с помощью граничных условий из (6.11),
получаем:
()
[]
()
(
)
()
211
22
211
221
1
2/1
,
1
2/1
BiBiBi
BiPoBi
D
BiBiBi
BiPoBiBi
C
++
−
+
=
++
−+
=
.
(6.13)
Координата максимума температуры находится из условия:
0/:
=
= dzduzz
m
.
(6.14)
Тогда для рассматриваемой задачи координата z
m
и соответствующее ей
максимальное значение температуры и безразмерные температуры поверхно-
стей стенок равны:
2
,
2
m
mmm
z
PoCzDu
Po
C
z −+==
,
(6.15)
()
(
)
2/1,0
21
PoCDzuuDzuu
−
+
=
=
=
===
.
(6.16)
При численном решении задачи граничные условия аппроксимируем со
вторым порядком по 3-х точечной формуле [23]. Разностный аналог краевой
задачи (6.11) имеет вид:
()
Pohuuu
iii
−=+−
−+
2
11
/2
, (1≤ i ≤ n-1)
(6.17)
()
,2/34
01012
uBihuuu
=
−
+−
(6.18)
()
(
)
.12/43
221 nnnn
uBihuuu
−
=
+−
−−
(6.19)

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
54
Преобразуем (6.18), (6.19) таким образом, чтобы исключить u
2
и u
n-2
. Ис-
пользуя (6.17), запишем его для точек i = 1, i = n –1:
,2
2
012
Pohuuu −=+−
(6.20)
.2
2
21
Pohuuu
nnn
−=+−
−−
(6.21)
Из системы (6.18) и (6.20) находим, что
1110
DuEu
+
=
,
(6.22)
где
(
)
(
)
(
)
.2/1/,1/1
1
2
111
PohBihDhBiE +=+=
(6.23)
Аналогично из системы уравнений (6.19), (6.21) получаем:
,
1
SRuu
nn
+
=
−
(6.24)
где
(
)
(
)
(
)
.2/1/,1/1
2
2
2
PohBihShBiR +=+=
(6.25)
Добавим к (6.22), (6.24) уравнение вида
PouLuMuK
iiiiii
−
=
+−
+− 11
(1≤ i ≤ n-1) .
(6.26)
Для вывода формул прогонки представим зависимость u
i
от u
i+1
по ана-
логии с (6.22) в форме
,
111 +++
+
=
iiii
DuEu
(6.27)
где E
1
и D
1
определяются согласно (7.32), а остальные коэффициенты по-
ка не известны. Наряду с (6.27) можем записать:
(
)
.
111
1111
iiiiii
iiiiiiii
DDEuEE
DuEEDuEu
++=
=
+
=
+
=
+++
+++−
(6.28)
Подставляя (6.27) и (6.28) в (6.26), имеем:
.0
11
11111
=++−
−
−
+
+
++
+++++
PouLDM
uEMDKDEKuEEK
iiii
iiiiiiiiiiii
(6.29)
Приравнивая в последнем соотношении отдельно коэффициенты при u
i+1
и свободные члены к нулю, приходим к системе уравнений:
.0
,0
11
11
=+−+
=
+
−
++
++
PoDMDKDEK
LEMEEK
iiiiiii
iiiiii
(6.30)
Отсюда получаем рекуррентные формулы для вычисления коэффициен-
тов прямой прогонки:
11,,
11
−≤≤
−
+
=
−
=
++
ni
EKM
PoDK
D
EKM
L
E
iii
ii
i
iii
i
i
.
(6.31)
Эти формулы позволяют по исходным значениям E
1
и D
1
из (6.23) вычис-
лить остальные n-1 коэффициента. Определив E
n
и D
n
, находим:
,
1 nnnn
QuEu
+
=
−
подставив которое в (6.24), получаем:
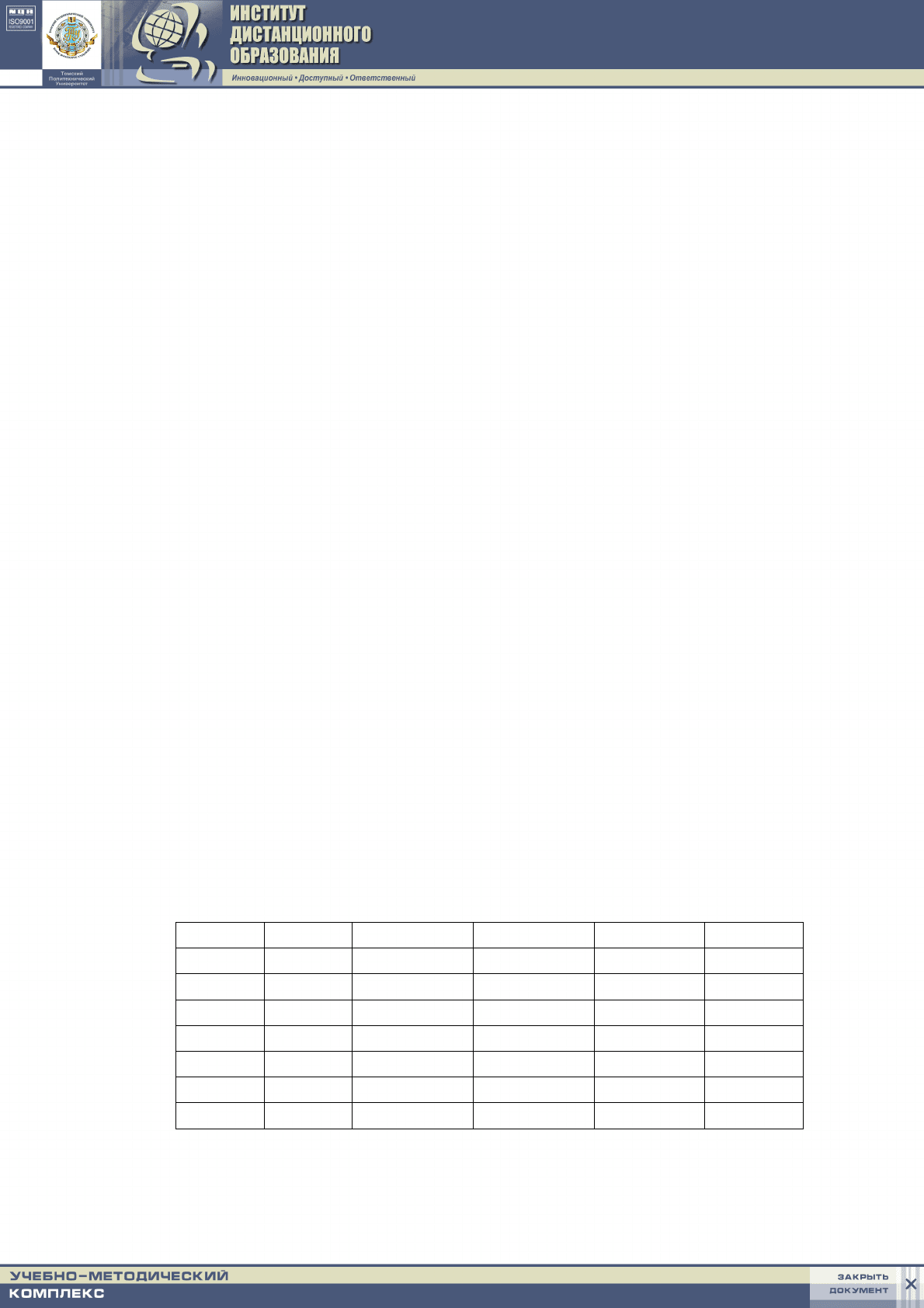
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
55
()
.SDuERu
nnnn
+
+
=
(6.32)
Отсюда:
(
)( )
(
)
.01,1/
≠
−
−
+=
nnnn
RERESRDu
(6.33)
Затем осуществляется обратная прогонка, которая заключается в вычис-
лении неизвестных u
i
(i = n-1, n-2, …,0) по формуле (6.27).
Доказано, что прогонка осуществима и устойчива, если выполняются не-
равенства [18], [20], [22], [23], [32]:
.10,10
,11,,0,0
1
≤≤<≤
−
≤
≤
+
≥>>
RE
niLKMLK
iiiii
(6.34)
Разностная схема рассматриваемой краевой задачи (6.11) при разбиении
отрезка интегрирования на 10 участков (n = 10) имеет следующие значения
коэффициентов в формулах прогонки:
.200/2,100/1
22
===== hMhLK
iii
Безразмерные параметры (6.10) и постоянные интегрирования (6.13) при-
нимают такие числовые значения:
2265,4,8242,0,1275,0,195,0
21
=
=
=
= DCBiBi
.
Координата и значение максимальной температуры, в соответствии с
формулами (6.15), равны
3
102,8,55,0
−
⋅==
mm
xz
м,
(
)
848,45,4
1,1,2,
=+
−
=
=
lmllmm
tutttu
0
С.
Температуры поверхностей стенок, согласно (6.16), принимают значения:
()
()
.825,3,42/
,814,2265,4
0
1,22,1,22
0
1,12,1,11
CtutttPoCDu
CtutttDu
lll
lll
=+−==−+=
=+−===
В табл. 6.2 представлены результаты вычисления безразмерных темпера-
тур аналитическим формулы (6.12), (6.13) и численным методами для ряда
значений координат, а также параметры прогонки.
Таблица 6.2
i z
i
u
a
u
i
E
i
D
i
0 0 4,2265 4,2265
2 0,2 4,3613 4,3136 0,9812 0,00219
4 0,4 4,4362 4,3873 0,9819 0,05032
5 0,5 4,4511 4,4011 0,9822 0,06416
6 0,6 4,401 4,4 0,9825 0,07778
8 0,8 4,406 4,3544 0,9831 0,1044
10 1,0 4,3086 0,9834 0,1174
Значения аналогичных параметров на второй поверхности теплообмена,
найденные по формулам (6.24), (6.25), равны:
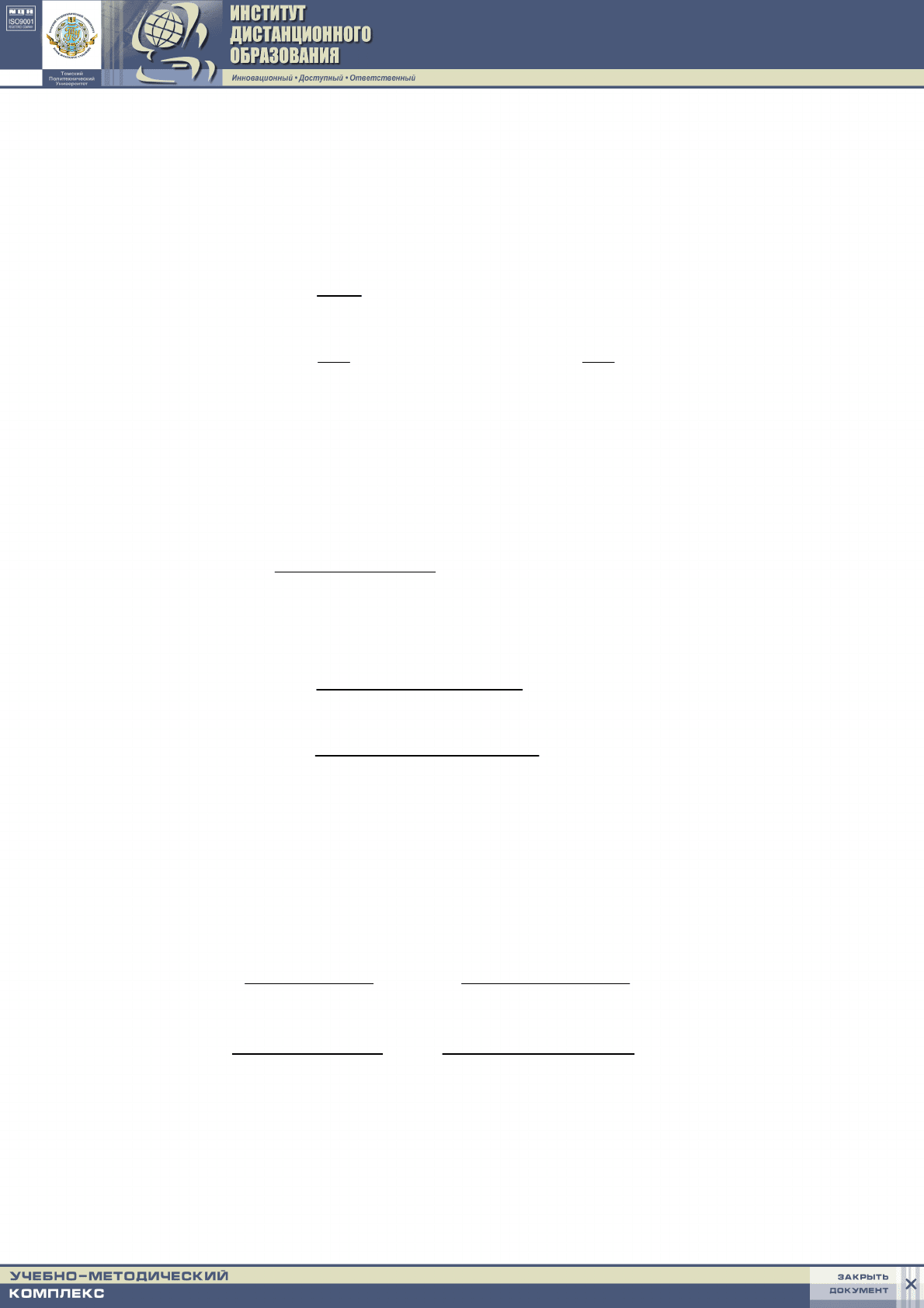
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
56
(
)
(
)
.248,41/,0074,0,9874,0
101010
=
−
+
=
== RESRDuSR
Пример 6.3. Рассмотрим более общую задачу, в которой как тепловыде-
ление, так и теплопотери в прямом стержне с постоянным сечением по длине
зависят от координаты. Граничные условия моделируют различные варианты
тепловой обстановки на оребренной поверхности [28], [48]. Математическая
постановка линейной краевой задачи в безразмерных переменных имеет вид:
() ()
,
2
2
ξξω
ξ
p
d
d
=Θ+
Θ
21022101
:,: g
d
d
ggk
d
d
kk =
Θ
+Θ==
Θ
+Θ=
ξ
γξ
ξ
γξ
.
(6.35)
Переходим к дискретному аналогу данной краевой задачи. Заменяем про-
изводные в уравнении и граничных условиях по формулам численного
дифференцирования на сетке [18-23]:
()
nini
i
≤
≤
−=ΔΔ+= 0,/,
121
γ
γ
ξ
ξ
γ
ξ
.
Для внутренних узлов ξi (1< i ≤ n-1) имеем:
iii
iii
p=Θ+
Δ
Θ
+Θ−
Θ
−+
ω
ξ
2
11
2
.
(6.36)
Граничные условия аппроксимируем со вторым порядком по 3-х точеч-
ной формуле:
()
,
2
34
2
0121
00
k
k
k =
Δ
Θ−Θ+Θ−
+Θ
ξ
(6.37)
()
.
2
43
2
211
0
g
g
g
nnn
n
=
Δ
Θ+Θ−Θ
+Θ
−−
ξ
(6.38)
Разностная схема (6.36) - (6.38) представляет собой систему из n + 1 урав-
нения с n + 1 неизвестными.
Для ее решения используем метод прогонки.
Как и в примере 6.2, осуществляем аналогичные преобразования. Полу-
чаем:
,,
11110
SQDE
nn
+
Θ
=
Θ
+Θ=Θ
−
()
()
(
)
()
;
2
2
,
2
2
01
112
1
01
2
11
1
ξ
ξξ
ξ
ξ
Δ−
ΔΔ+
−=
Δ−
Δ+
=
kk
pkk
D
kk
pk
E
(
)
()
(
)
()
.
2
2
,
2
2
01
112
01
2
11
ξ
ξξ
ξ
ξω
Δ+
ΔΔ−
=
Δ+
Δ+
=
−−
gg
pgg
S
gg
g
Q
nn
(6.39)
Рекуррентные формулы прямой прогонки:
,
111 +++
+
Θ
=Θ
iiii
DE
(6.40)
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
57
где коэффициенты E
1
и D
1
вычисляются из (6.39), а остальные – по форму-
лам (6.41)
()
.11,,
11
−≤<
−
−
=
−
=
++
ni
EAC
pDA
D
EAC
B
E
iii
iii
i
iii
i
i
(6.41)
Определив E
n
и Dn , находим:
(
)( )
.01,1/
≠
−
−
+=Θ
nnnn
QEQESQD
(6.42)
Затем осуществляем обратную прогонку, которая заключается в вычисле-
нии неизвестных Θi (i = n -1, n - 2, …,0) по формуле (6.40).
Для уточнения условий осуществимости и устойчивости прогонки, про-
веряем, выполняются ли неравенства в рассматриваемом методе:
.10,10,,0,0
≤
≤
<
≤
+
≥>> QEBACBA
iiiiii
(6.43)
Описанный алгоритм прост и легко программируется.
6.2. Двухмерные стационарные задачи теплопроводности
При расчете температуры в деталях сложной формы возникает необходи-
мость учета неодномерности ее распределения. Получить аналитическое ре-
шение двумерной задачи теплопроводности сложнее, чем одномерной, да и
сами зависимости имеют громоздкий вид, поэтому чаще используются чис-
ленные методы.
При использовании численного метода конечных разностей твердое тело
представляют в виде совокупности ячеек (узлов), в виде ра
вных элементар-
ных прямоугольников, имеющих длину Δx в направлении x и ширину Δy в
направлении y. Для каждого узла (внутри и на границе твердого тела) запи-
сывается баланс энергии, в итоге получается n алгебраических уравнений от-
носительно температуры. Если узлов в твердом теле сравнительно мало, то
полученную систему алгебраических уравнений обычно решают метод
ом
Гаусса. Для высокого порядка системы применяют специальные алгоритмы
(метод обращения матрицы, итерационный метод).
Пример. 6.4. Найти стационарное распределение температуры в двумер-
ном теле, представляющем собой квадрат (рис.6.1) со стороной 0,02 м и ко-
эффициент теплопроводности λ = 1 Вт/(м⋅К). На верхней и нижней границах
поддерживаются постоянные температуры, равные t
s,1
= 100
0
С и t
s,2
= 200
0
С;
правая поверхность теплоизолированная, а на левой происходит конвектив-
ный теплообмен с окружающей средой, имеющей температуру t
c
= 50
0
С и
коэффициент теплоотдачи α = 50 Вт/(м
2
⋅К).
Опишем методику решения сформулированной выше двухмерной ста-
ционарной задачи теплопроводности методом конечных разностей.
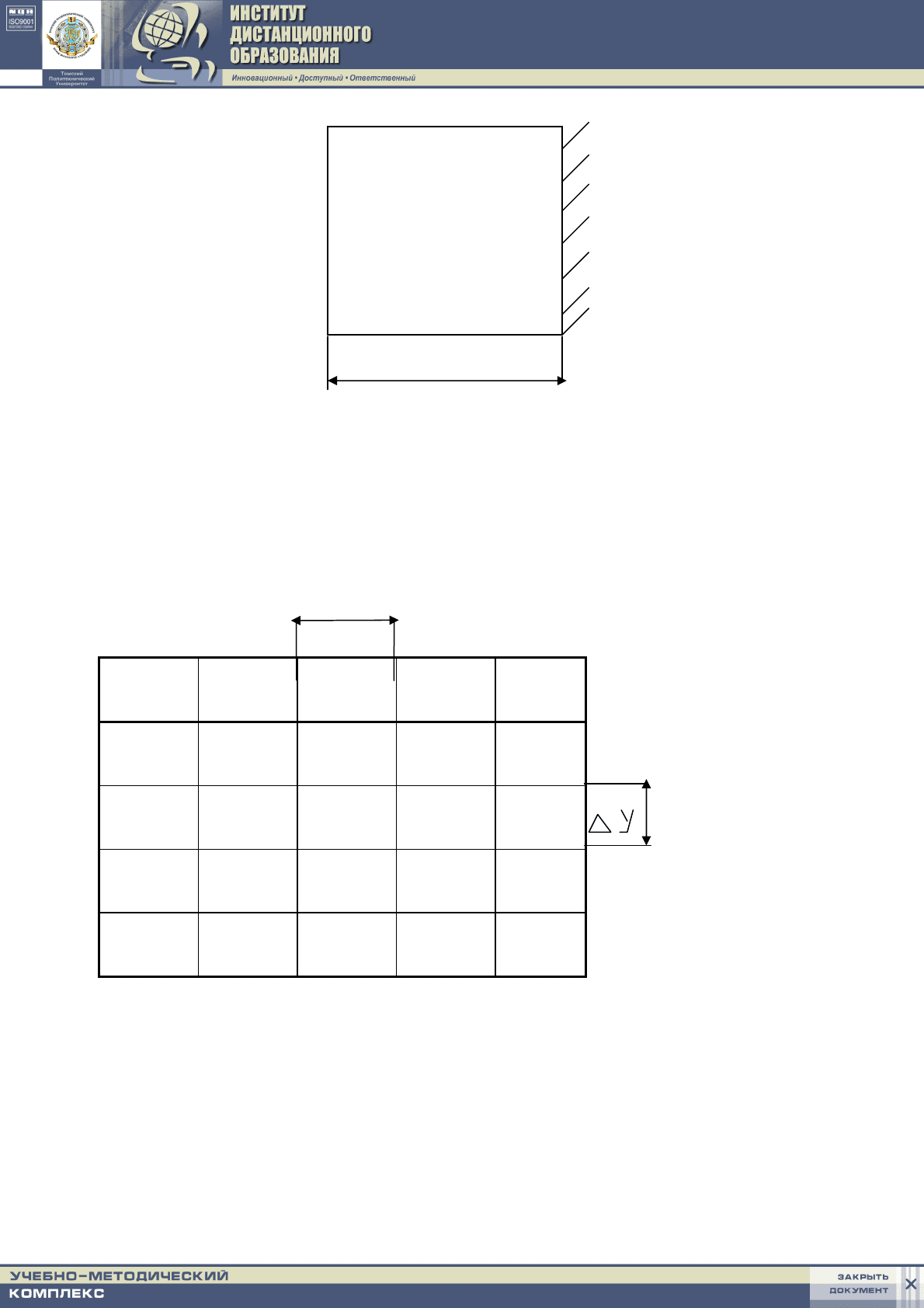
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
58
t
s1
= 100
0
C
α = 50 Вт/ (м
2
К)
t
c
= 50
0
C
t
s1
= 100
0
C
0.2 м
Рис. 6.1. Схема нагрева пластинки
Твердое тело (рис.6.2) делится на 15 ячеек квадратной формы Δx = Δy =
0,05 м. Температуры в узлах верхней и нижней поверхностей известны, нуж-
но найти температуры в 15 узлах. Узел, находящийся в центре каждой ячей-
ки, называется центральным и обозначается символом 0. Он окружен че-
тырьмя соседними узлами.
ΔХ
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
Рис 6.2 Расположение сетки для численного решения задачи
В установившихся условиях баланс энергии для узла 0 при отсутствии
внутреннего тепловыделения записывается в форме
.0
4
1
0
=
∑
=
→
i
i
q
(6.44)
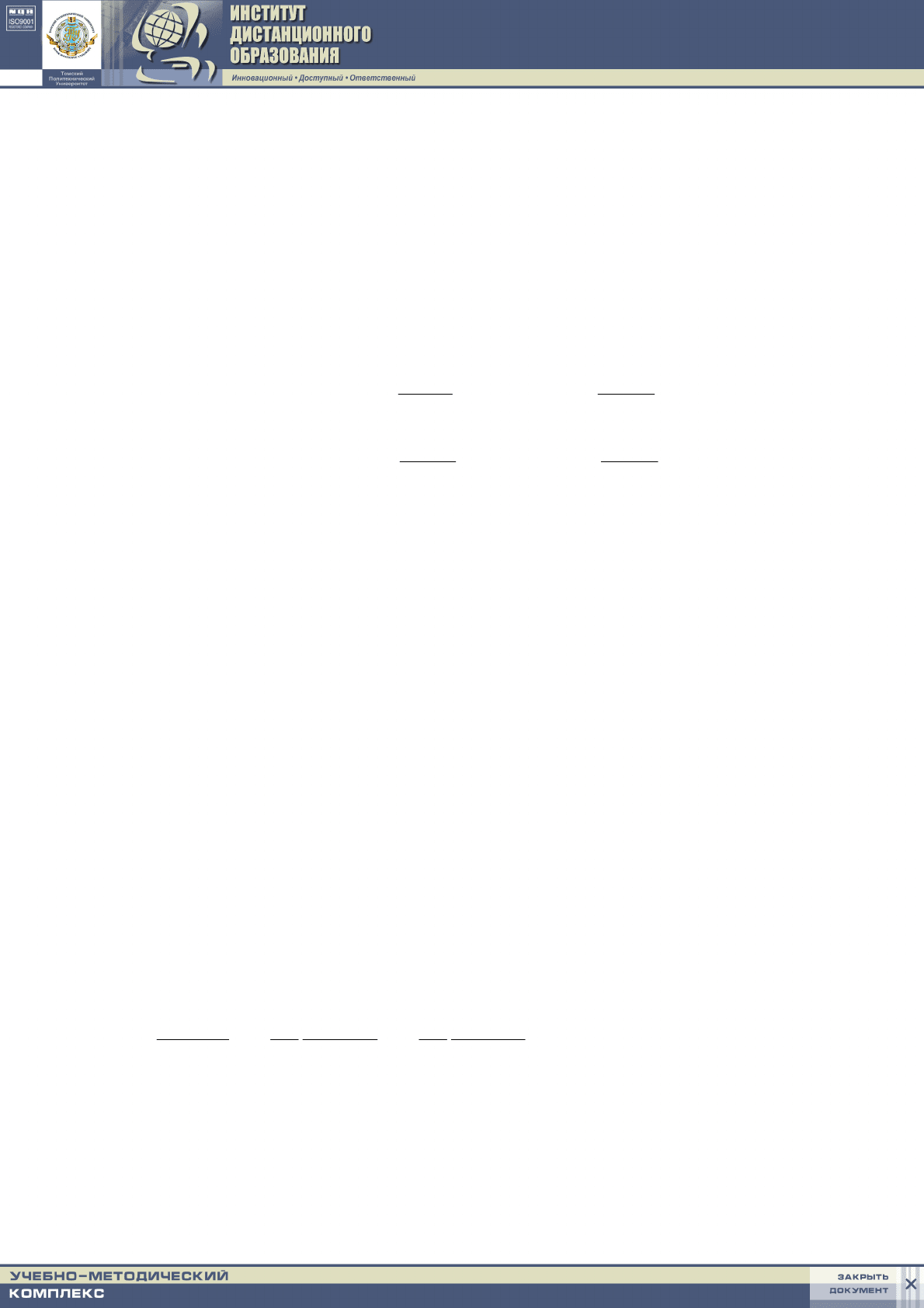
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
59
Тепловые потоки в направлениях x и y определяются с помощью закона
Фурье и выражаются следующим образом:
./,/ ytqxtq
yx
∂
∂
−
=
∂
∂−=
λ
λ
(6.45)
С применением этого закона для каждого члена и формулы правой разно-
сти для производных уравнение (6.44) выражается через температуры в уз-
лах:
,,
,,
04
04
03
03
02
02
01
01
y
tt
xq
x
tt
yq
y
tt
xq
x
tt
yq
Δ
−
Δ−≈
Δ
−
Δ−≈
Δ
−
Δ−≈
Δ
−
Δ−≈
→→
→→
λδλδ
λδλδ
где δ - толщина двумерного тела по нормали к плоскости чертежа, а градиент
температуры определяется посередине между узлами. Точность его замены
разностью двух температур повышается с уменьшением размера ячейки.
После подстановки четырех конечно-разностных соотношений в уравне-
ние (6.44) видно, что для сетки с квадратными ячейками при постоянном ко-
эффициенте теплопроводности баланс энергии для центр
ального узла при-
нимает вид:
.04
04321
=
−
+
++ ttttt
(6.46)
Это выражение применимо ко всем внутренним узлам, т.е. ко всем узлам,
не лежащим на границе твердого тела и окруженным со всех сторон равноот-
стоящими квадратными ячейками сетки.
Баланс энергии для узла 0, расположенного на границе, который может
обмениваться кондуктивным потоком тепла с тремя соседними узлами в
твердом теле и конвективным тепловым потоком с окружающей средой име-
ет вид:
() ()
(
)
()
.0
22
0
030201
=−Δ+
Δ
−
Δ
+
Δ
−
Δ
+
Δ
−
Δ tty
y
tt
x
y
tt
x
x
tt
y
c
αλλλ
(6.47)
Для ячейки квадратной формы это соотношение упрощается и сводится к
виду:

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
60
()
(
)
,022/
0132
=
+
−
+++ tBiBitttt
c
(6.48)
где Bi = αΔx ⁄λ - критерий Био с характерным размером, равным стороне
квадрата.
Применяя описанную методику составления балансовых уравнений для
ячеек применительно к рассматриваемому примеру и учитывая числовые
значения (Bi = 2,5, Bi⋅t
c
= 125
0
С, 2 + Bi = 4,5), получаем последовательно для
каждого узла систему уравнений 6.49.
Для решения этой системы используем метод Гаусса, который описан в
гл. 2, и где приведена распечатка программы.
.5025,0:15
,1004:14
,1004:13
,1004:12
,1755,45,0:11
,05,025,0:10
,04:9
,04:8
,04:7
,1255,05,45,0:6
,1005,02:5
,2004:4
,2004:3
,2004:2
,2255,05,4:1
151410
1514139
1413128
1312117
12116
151095
1410984
139873
128762
11761
1054
9543
8432
7321
621
−=−++
−=+−+
−=+−+
−=+−+
−=+−
=+−+
=++−+
=++−+
=++−+
−=++−
−=+−
−=++−
−=++−
−=++−
−=++−
ttt
tttt
tttt
tttt
ttt
tttt
ttttt
ttttt
ttttt
tttt
ttt
tttt
tttt
tttt
ttt
(6.49)
Введя последовательно коэффициенты системы (6.50), получаем в итоге
величины температур в узлах сетки:
.7,118;9,116;7,110;8,96;1,68
;9,140;3,138;0,129;5,108;3,69
;4,168;3,166;6,158;9,138;6,88
1514131211
109876
54321
=====
=====
=
=
=
==
ttttt
ttttt
ttttt
Пример 6.5. Необходимо найти распределение температур в квадратной
пластинке со стороной, равной четырем безразмерным единицам, если две
