Голдаев С.В., Ляликов Б.А. Основы математического моделирования в теплотехнике
Подождите немного. Документ загружается.


Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
71
(
)
()
⎩
⎨
⎧
=
=
xzygdxdz
xzyfdxdy
,,/
,,,/
(7.16)
записываются следующим образом
()()
()
()
()
()
()()
[]
()
[]
.6/2
,6/)(2
,,,,,,
,2/,2/,2/
,2/,2/,2/
,2/,2/,2/
,2/,2/,2/
,,,,,,
43211
43211
334334
223
223
112
112
11
hnnnnzz
hmmmmyy
nzmyhxgnnzmyhxfm
nzmyhxgn
nzmyhxfm
nzmyhxgn
nzmyhxfm
zyxgnzyxfm
kk
kk
kkkkkk
kkk
kkk
kkk
kkk
kkkkkk
++++=
++++=
+++=+++=
+++=
+++=
+++=
+++=
==
+
+
(7.17)
Схема (7.17) обобщается на системы обыкновенных дифференциальных
уравнений произвольного порядка. Для удобства программной реализации,
особенно в случае систем, формулы (7.17) преобразовывают к виду [25]
()
(
)
(
)
,3/2
432100 iiiiii
qqqqyhxy
+
+
+
+
=+
()
(
)
()()
,,,,
,,,2/,,
30024130203
10202220021
iiiiiii
iiiiiii
qyhxfhqqyhxhfq
qyhxfhqhhyxfhq
++=++=
+
+
=
==
(7.18)
где i = 1,2, …, n – номер уравнения в системе n – го порядка.
На рис. 7.2 изображена блок- схема, реализующая описанные методы.
Ввод: n - порядок системы,
x
0
, y
0
- начальные условия,
h, x
9
- шаг и конечная точка
интегрирования
Циклическое изменение аргумента x
Метод
интегрирования
ВВывод таблицы
x
,
y
1
, …,
y
n
Вычисление пра-
вых
частей системы
Рис.7.2. Блок – схема решения задачи Коши явными методами
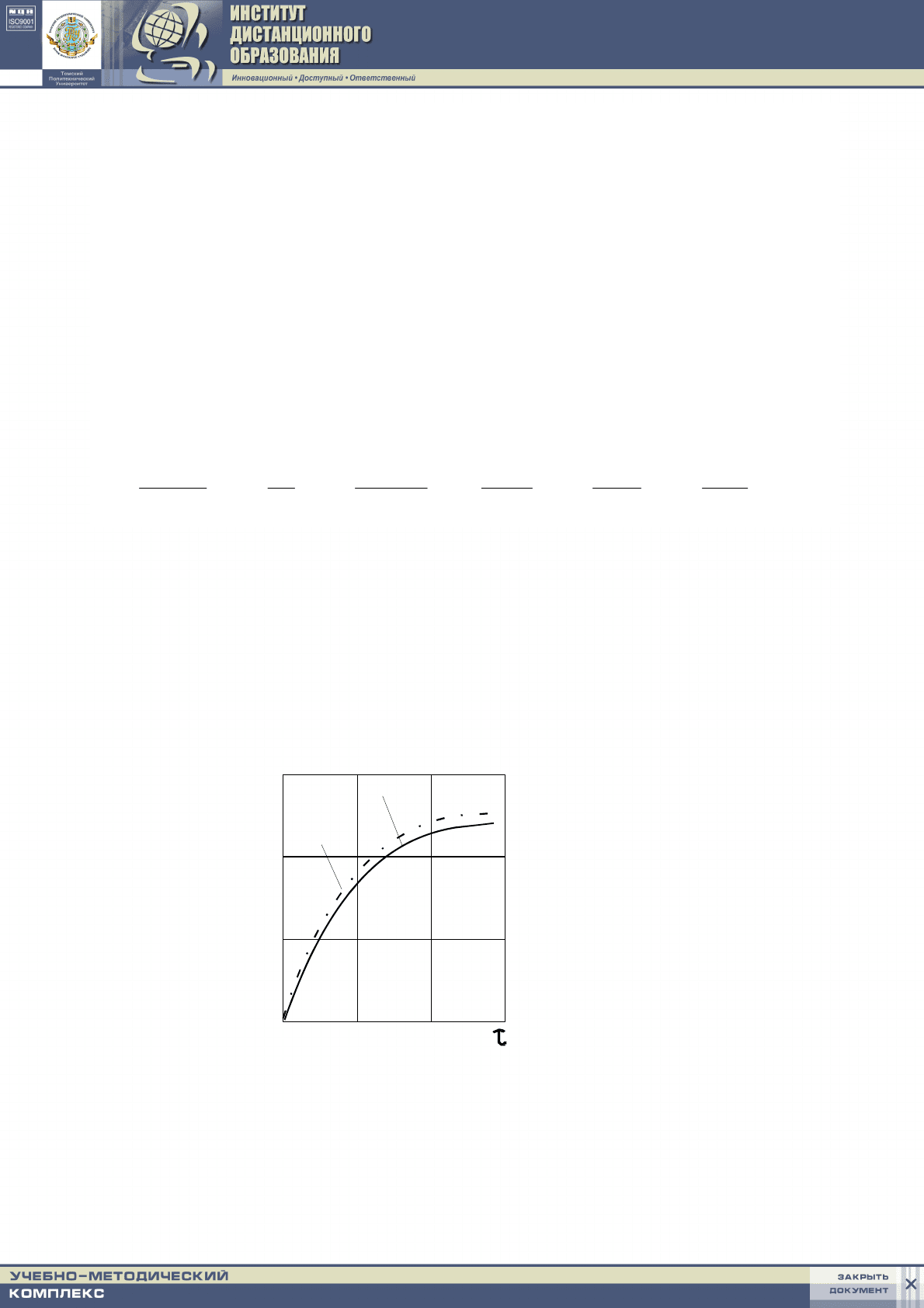
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
72
принимает вид:
()( )
(
)
;0:0,1/ =
=
−
+
+= uuCuABddu
nlln
τ
τ
τ
τ
.707,1,5,0,631,0,072,2
−
=
−
=
=
=
CABu
l
Численное решение осуществлялось методом Эйлера-Коши:
()
(
)
(
)
(
)
,1,,,
,,,,1, kknlknknkknkkkb
uCuAufuhfuu −++=+=
+
ττττ
()
(
)
(
)
[
]
kbknkknkk
ufufhuu
,,,1
,,2/
ττ
++=
+
.
Результаты расчетов представлены на рис. 7.3.
Рис. 7.3. Результаты решения задачи Коши модифицированным
методом Эйлера
u
0,4
0,2
0,0
0 0,4 0,8
h=0.25
h=0.05
Рассмотрим их применение при решении ряда задач.
Пример 7.2. Одна из поверхностей стальной пластины (c = 602
Дж/(кг⋅К), ρ = 7900 кг/м
3
), толщиной δ = 2 мм и неограниченной протяженно-
сти, теплоизолирована, а другая находится во взамодействии с окруающей
средой, температура и коэффициент теплоотдачи которой измеяются со вре-
менем:
()
(
)
τ
τ
τ
α
τ
α
110
, kTTg
ic
+
=
+=
,
где α
0
= 600 Вт/(м
2
К) , g
1
= 30 Вт/(м
2
Кс), T
l
= 900 К, k
1
= -30 К/с. Необходи-
мо численно рассчитать изменение ее температуры в течение первых τ
p
=10 с.
Влиянием лучистого теплообмена и градиентом температуры поперек стенки
можно пренебречь.
Решение. Уравнение теплового баланса для пластины и начальное усло-
вие в безразмерных переменных, определяемых формулами
l
ppp
H
Hl
l
pH
H
T
k
C
g
A
c
B
T
TT
uf
T
TT
u
τ
α
τ
ρδ
τ
α
τ
τ
1
0
10
,,,,, ===
−
==
−
=
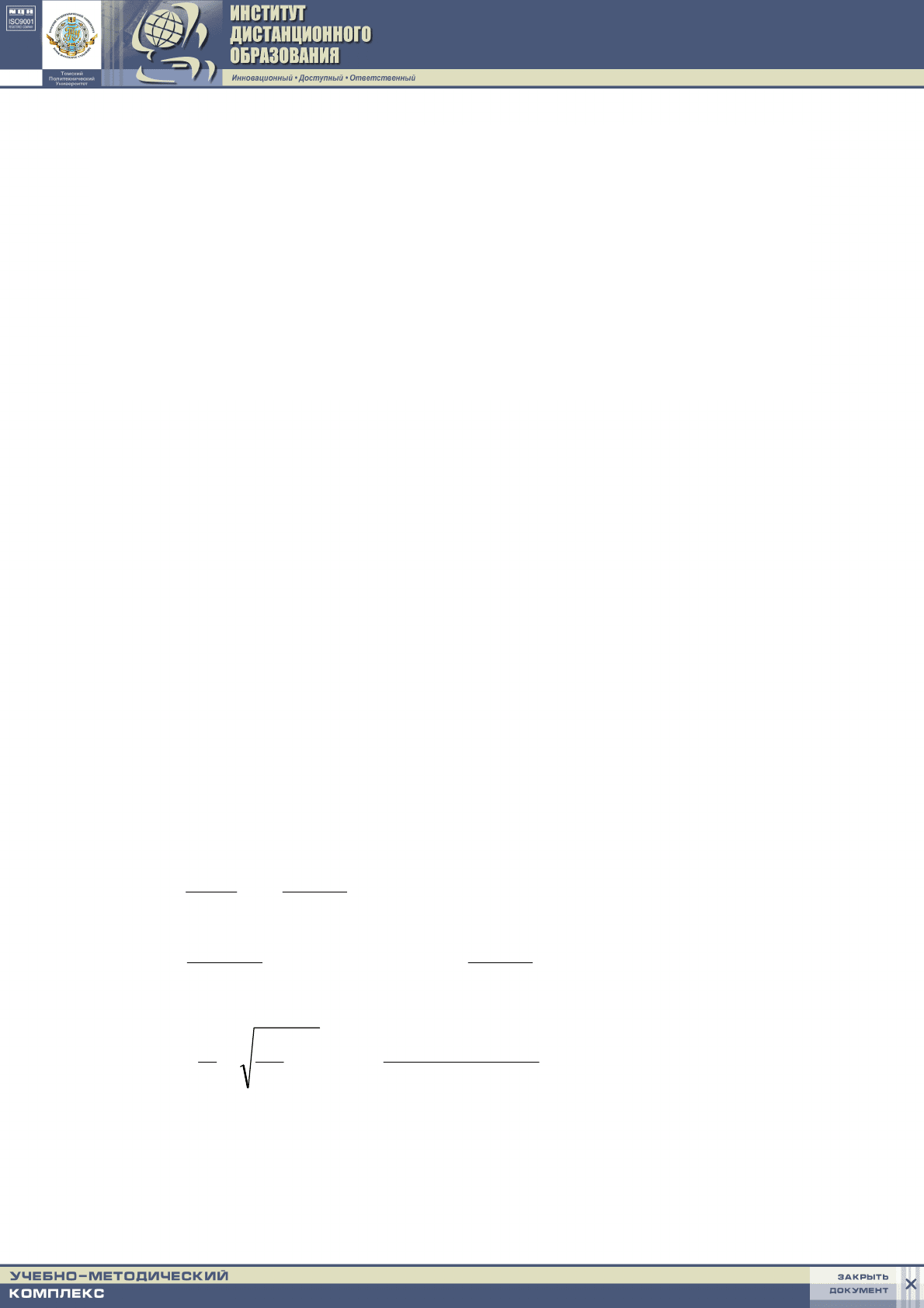
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
73
() ( )
(
)
(
)
(
)
() () ()
() () ()
./
,/
,/
32123
2112
32211211
tPtPdttdP
tPtPdttdP
tPtPtPdttdP
μλ
λ
μ
μ
λ
λ
−=
−=
+
+
+
−=
Начальные условия имели вид:
.0,0,1:0
321
=
=
=
= PPPt
Здесь λ
1
=2⋅10
-4
1/ч, λ
2
=1⋅10
-4
1/ч – интенсивности отказов элементов, μ
1
=1⋅10
-2
1/ч, μ
2
=1,25⋅10
-2
1/ч – интенсивности их восстановления;
P
0
, P
1
, P
2
– вероятности состояний системы, связанные условием нормировки
()
(
)
(
)
.1
321
=
+
+
tPtPtP
Поскольку работоспособным является только первое состояние, то не-
обходимо решить систему относительно P
1
(t). Стационарный коэффициент
готовности k
G
, который характеризует заложенную способность обеспечения
непрерывной работы при правильном использовании и обслуживании уста-
новки, равен этой вероятности.
В пособии [10] с помощью преобразования Лапласа было получено ана-
литическое выражение для P
1
(t), которое имело вид:
() () ()
[]
() ()
[]
() ()
[]
,expexp
1
expexp
expexp
1
1
2211
21
21
21
21
2112
2121
21
1
tsstss
ss
tsts
ss
tsstss
ssss
tP
−
−
+−
−
+
+
+
⎭
⎬
⎫
⎩
⎨
⎧
−
−
+=
μμ
μμ
где
.,
2
,
42
122121
2121
2
2,1
μλμμμλ
μμλλ
++=
+++
=−±−= qpq
pp
s
Из найденного решения следует, что при t = 0, P
1
(t) =1, а для t →∝
P
1
(t) = μ
1
μ
2
/q. Для данного варианта значений интенсивностей отказов и вос-
становлений величина коэффициента готовности k
G
= P
1
= 0,972.
Дальнейшее уменьшение шага интегрирования в два раза показало,
что отличие безразмерных температур не превышает 0,2%.
Пример 7.3. Вероятностная математическая модель функционирова-
ния различных систем, основанная на использовании марковских процес-
сов, сводится к решению системы Колмогорова – Чепмена [9], [10]. Коли-
чественный анализ показателей надежности энергоблока, состоящего из
котла и турбоагрегата, проведенный в [10], свелся к следующей системе
трех линейных дифференциальных уравнений, описывающих вероятно-
сти возмо
жных состояний:

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
74
Сформулированная задача Коши была решена численно по методу Рунге
– Кутта. Ниже представлен листинг программы, а далее –результаты в виде
таблицы значений безразмерного времени и соответствующих ему величин
вероятностей состояния
.
program rukus (input, output);
uses crt;
const l1=0.0002; l2 =0.0001;m1=0.01;m2=0.0125; tp=400; tch=242;
type vec = array [1..8] of real;
var p,x,x9,h,t: real; y:vec;
procedure rp(x:real; var y,f:vec); (*proisvodn*)
begin
f[1]:=-(l1+l2)*tp*y[1]+m1*tp*y[2]+m2*tp*y[3];
f[2]:=l1*tp*y[1]-m1*tp*y[2];
f[3]:=l2*tp*y[1]-m2*tp*y[3];
end;
procedure rk4(n:integer; x,h:real; var y:vec);
var i,j:integer;
h1,h2,q:real; y0,y1,f:vec;
begin
h1:=0.0; h2:=h/2;
for i:=1 to n do
begin
y0[i]:=y[i];
y1[i]:=y[i];
end;
for j:=1 to 4 do
begin
rp(x+h1,y,f);
if j=3 then h1:=h else h1:=h2;
for i:=1 to n do
begin
q:=h1*f[i];
y[i]:=y0[i]+q;
if j=2 then q:=2*q;
y1[i]:=y1[i]+q/3.0
end
end;
for i:=1 to n do y[i]:=y1[i]
end;
begin
clrscr;
repeat
write (' Введите x,x9,h,y[1],y[2],y[3]: ');

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
75
readln (x,x9,h, y[1],y[2],y[3]);
x:=1; x9:=1.5; H:=0.05; y[1]:=1; y[2]:=1;
while (x<x9)=(h>0.0) do
begin
rk4(3,x,h,y);
x:=x+h; t:=x*tp;
writeln (' x=',x:5:3,' t=',t:5:3,' y1=', y[1]:6:4,' y2=',y[2]:6:4,' y3=',y[3]:6:4)
end;
writeln(' Для выхода нажмите Esc, для продолжения - другую
клавишу');
until readkey=#27
Введите x,x9,h,y[1],y[2],y[3]: 0 1 0.1 1 0 0
t= 80.0 y1=0.9841 y2=0.0109 y3=0.0050
t=160.0 y1=0.9775 y2=0.0157 y3=0.0068
t=240.0 y1=0.9748 y2=0.0178 y3=0.0074
t=320.0 y1=0.9736 y2=0.0187 y3=0.0077
t=400.0 y1=0.9731 y2=0.0191 y3=0.0077
На рис. 7.4 для удобства анализа графически изображено изменение k
G
со временем. Видно, что при t > 400 ч он приближается к своему стационар-
ному значению. Сравнение k
G
, полученное разностным методом с вычислен-
ным по аналитической формуле, показало их хорошее количественное соот-
ветствие.
Рис. 7.4. Изменение коэффициента готовности со временем
k
G
0,99
0,98
0,98
0 200 400 t,ч

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
76
7.3. Методы решения задач нестационарной теплопроводности
Разработано множество алгоритмов точного решения задач нестацио-
нарной теплопроводности. Кроме изучаемого в рамках традиционного курса
теплотехники способа разделения переменных [28], [30], [41], применяются
методы конформных отображений, функций источников, тепловых потен-
циалов, конечных и бесконечных интегральных преобразований и ряд других
[19], [21], [30], [43], [50]. Однако их описание и использование предполагает
знакомство с элементами теории функций комплексного переменного, кото-
рые не включены в программы изучения высшей математики в технических
университетах и не будут рассматриват
ься в рамках данного пособия.
Остановимся вначале на кратком изложении инженерных методов ре-
шения задач нестационарной теплопроводности, для понимания которых и
овладения методикой их применения достаточно уметь интегрировать и ре-
шать простейшие обыкновенные дифференциальные уравнения.
7.3.1. Приближенные аналитические методы решения
нестационарных задач теплопроводности
В этих методах используется инженерная модель процесса теплопро-
водности, согласно которой предполагается, что подводимый тепловой поток
постепенно проникает в глубь нагреваемого тела. Толщина термического
слоя при этом непрерывно увеличивается, и только через определенный от-
резок времени тело прогревается по всему сечению. В этот момент заканчи-
вается этап начального (инерционного) и начинается стадия регулярного
(упорядоченного) нагр
ева, характеризуемого участием всего тела в процессе
нагрева [19], [21].
Интегральный метод теплового баланса позволяет получать приближен-
ные решения ряда нелинейных задач нестационарной теплопроводности пу-
тем сведения дифференциального уравнения в частных производных к обык-
новенному.
Для уяснения методики его применения рассмотрим следующую задачу,
моделирующую воздействие на плоский образец тепловым потоком [30
],
[42]. Найти распределение температур в полуограниченном стержне, которое
описывается второй краевой задачей теплопроводности:
0,0,//
22
>>∂∂=∂∂
rr
xxTaT
ττ
()
(
)
(
)
.,;/;0,
00
TxTqxTTxT
rr
=
∞
=∂∂
−
=
τ
λ
(7.19)
Усредняем уравнение (7.19) путем интегрирования его по координате от
0 до x , равного толщине термического слоя δ(τ) :
()
(
)
.
0
2
2
0
∫∫
∂
∂
=
∂
∂
τδτδ
τ
dx
x
T
adx
T
(7.20)
Выполняя эту операцию, получаем:

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
77
()
[]
()
(
)
()
(
)
.,
1
,
,0,
0
0
∫
=Θ
⎥
⎦
⎤
⎢
⎣
⎡
∂
∂
−
∂
∂
=−Θ
τδ
τ
δ
ττδ
τδ
τ
dxxT
x
T
x
T
aT
d
d
(7.21)
Вместо условия на бесконечности ставится условие на границе толщины
термического слоя:
(
)
,,
0
TT
=
τ
δ
(7.22)
(
)
.0/,
=
∂
∂
xT
τ
δ
(7.23)
Решение дифференциального уравнения (7.22) с условием на поверхно-
сти из (7.19) и при x = δ - (7.22), (7.23) ищем в виде полинома второй степени
,
2
210
xaxaaT ++=
(7.24)
коэффициенты которого в общем случае зависят от времени.
Подставляем (7.24) в упомянутые граничные условия, получаем систему
трех линейных алгебраических уравнений относительно коэффициентов a
i
,
решая которую имеем:
()
(
)
(
)
[
]
()
.
2
,
2
0
τλδ
τδτ
τ
xq
TxT
−
+=
(7.25)
Для определения неизвестной функции δ(τ) используется уравнение
(7.21). Интеграл теплового баланса (7.20) с учетом граничного условия из
(7.19) и (7.23), а также выражения
()
(
)
∫
+==Θ
τδ
λ
δ
τ
δ
0
0
6
,
1 q
TdxxT
преобразуется в следующее обыкновенное дифференциальное уравнение
первого порядка относительно δ(τ):
(
)
(
)
ττδ
aqdqd 6/
2
=
(7.26)
с начальным условием
(
)
.00
=
δ
В уравнении (7.26) переменные разделяются, и решение имеет вид:
() ()
[]
()
∫
=
τ
ττττδ
0
/6 dqqa
.
(7.27)
Полагая x = 0 в (7.25) и подставляя туда найденную толщину термиче-
ского слоя, определяем температуру поверхности нагреваемого тела:
()
()
()
()
.
6
2
,0
0
0
∫
⎥
⎦
⎤
⎢
⎣
⎡
+=
τ
ττ
τλ
τ
τ
dq
q
a
q
TT
(7.28)
В частном случае постоянной плотности теплового потока q(τ) = q
1
из
(7.27) и (7.28) следует:

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
78
() ()
.
2
3
,0,6
1
0
τ
λ
τττδ
a
q
TTa +==
(7.29)
Точное решение этой задачи при q(τ) = q
1
имеет вид [43]:
()
.
4
,0
1
0
π
τ
λ
τ
a
q
TT +=
(7.30)
Сравнение (7.29) и (7.30) показывает, что они отличаются только значениями
числовых коэффициентов:
23,12/3,13,1/4 ≅≅
π
и эта разница составляет
примерно 9%.
Погрешность приближенного решения можно уменьшить, если исполь-
зовать аппроксимирующие полиномы (7.24) более высокого порядка.
Метод интегрального
π
/4 теплового баланса применяется и для реше-
ния стационарных краевых задач теплопроводности, рассмотренных в гл. 6.
Метод Швеца является итерационным и схема его применения иллюст-
рируется решением задачи, рассмотренной в предыдущем примере.
Первое приближение находится из решения следующей стационарной
задачи:
,0/
2
1
2
=dxTd
(7.31)
(
)
.:,/:0
0111
TTxqdxdTx
=
Δ
=
=
−=
τ
λ
(7.32)
Интегрируя (7.31) и определяя произвольные постоянные с помощью
граничных условий (7.32), получаем:
(
)
(
)
./
101
xqTT
−
Δ
+
=
λ
(7.33)
Подставляя (7.33) в исходное уравнение, приходим к краевой задаче для
нахождения второго приближения:
τ
∂
∂
=
∂
∂
1
2
2
2
T
x
T
a
,
(7.34)
12
/:0 qdxdTx
=
−
=
λ
,
(7.35)
(
)
.:
02
TTx
=
Δ
=
τ
(7.36)
Вычисляя производную ∂T
1
/∂τ с помощью (7.33) и подставляя в правую
часть (7.34), получаем неоднородное линейное обыкновенное дифференци-
альное уравнение, решение которого, с учетом (7.35), (7.36) имеет вид:
() ()
()
.,
2
,
1
22
1
02
τ
λ
λ
d
d
a
q
kx
k
x
q
TxT
Δ
=Δ−+−Δ+=Δ
(7.37)
Привлекая условие Швеца (обращение в нуль градиента температуры на
границе толщины термического слоя в i – ом приближении), приходим к
обыкновенному дифференциальному уравнению относительно Δ:
.//
Δ
=
Δ
add
τ
(7.38)
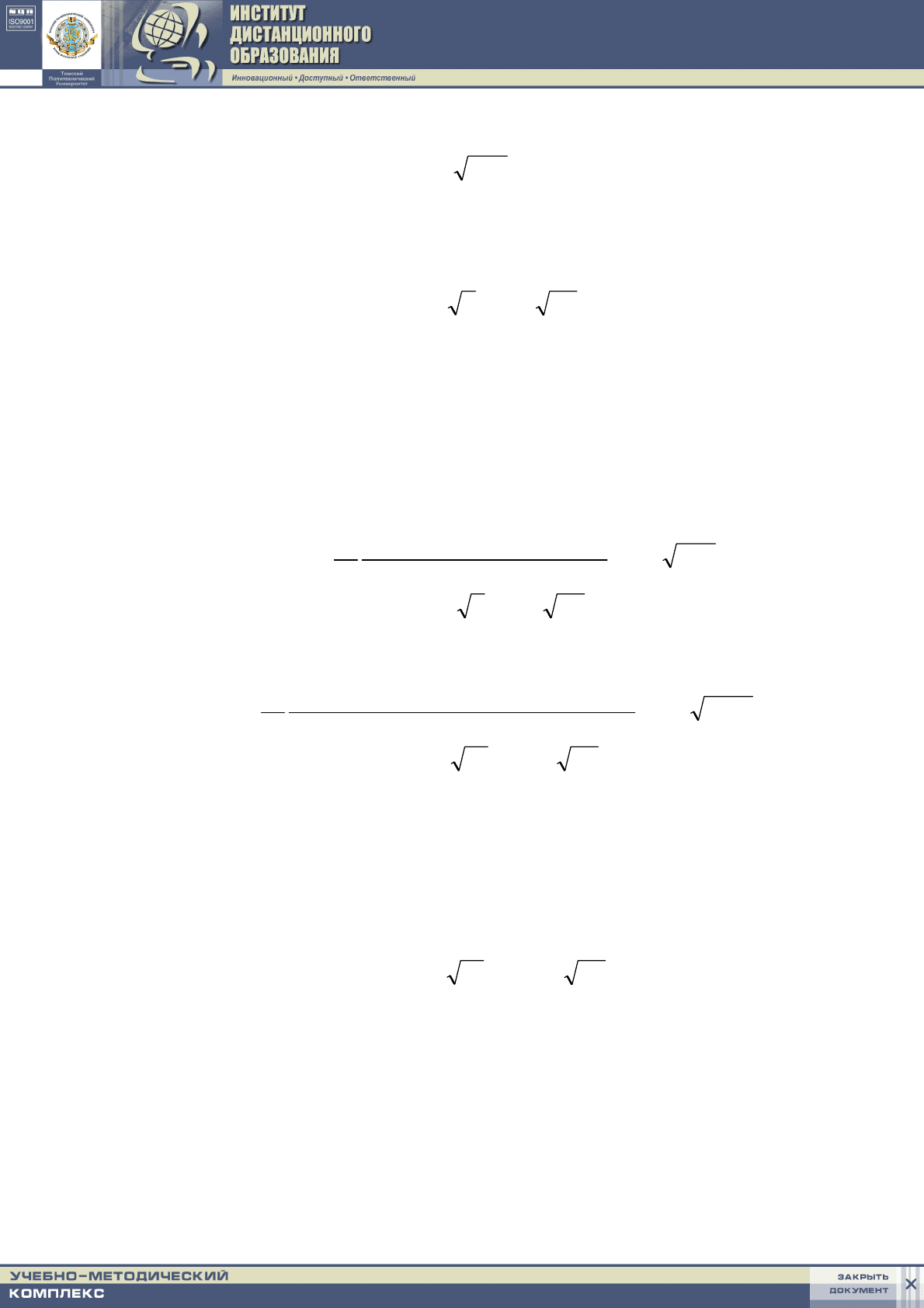
Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
79
Интегрируя его при нулевом начальном условии, получаем:
τ
a2=Δ
.
(7.39)
Подставляя (7.38) и (7.39) в (7.37) и полагая в нем x = 0, для температу-
ры поверхности имеем следующее выражение:
()
(
)
(
)
./2/2,0
102
λττ
aqTT +=
(7.40)
Сравнение его с точным решением (7.30) показывает, что структура вы-
ражения совпадает, а отличие числовых коэффициентов составляет около
37%.
Аналогичным образом находятся и следующие приближения. Так, после
третьей итерации получаем:
погрешность ее снижается до 18,5%;
()
(
)
;6,
8
683
,
3
42234
1
03
τ
λ
a
xxx
q
TxT =Δ
Δ
−Δ+Δ−Δ
+=Δ
(7.41)
()
(
)
(
)
λττ
/8/63,0
103
aqTT +=
,
(7.42)
четвертая итерация дает:
()
(
)
;10,
16
515165
,
5
6422456
1
04
τ
λ
a
xxxx
q
TxT =Δ
Δ
+Δ−Δ+Δ−Δ
+=Δ
(7.43)
()
(
)
(
)
λττ
/16/105,0
104
aqTT +=
,
(7.44)
точность ее составляет 12,5% процентов;
в пятом приближении распределение температуры по толщине образца опи-
сывается полином восьмой степени, который здесь не приводится из-за своей
громоздкости, а для температуры поверхности получено следующее выраже-
ние, имеющее погрешность около 9,3%.
()
(
)
(
)
./128/1435,0
105
λττ
aqTT +=
(7.45)
Пример 7.4. Найти изменения температуры поверхности кирпичной клад-
ки из красного кирпича (λ = 0,67 Вт/(м⋅К), a = 4,985⋅10-7 м
2
/с) со временем
при воздействии тепловым потоком плотностью q
1
= 10 кВт/м
2
. На рис 7.5
представлены результаты расчета на основе точного и приближенного реше-
ний.

Голдаев С.В., Ляликов Б.А. Основы математического моделирования
в теплотехнике: Учебное пособие. - Томск: Изд. ТПУ, 1999. – 106 с.
80
Рис. 7.5. Зависимость температуры поверхности
нагреваемого образца от времени
7.3.2. Численные методы решения задач нестационарной
теплопроводности
Для построения разностной схемы, как и в случае обыкновенных диф-
ференциальных уравнений, частные производные заменяются конечно-
разностными соотношениями по некоторому шаблону. При этом точные зна-
чения искомой функции заменяются значениями сеточной функции в узлах
разностной сетки с некоторыми погрешностями. Разностная схема называет-
ся сходящейся, если при сгущении узлов сетки это значение погрешности
стремит
ся к нулю. Разностная схема называется устойчивой, если ее решение
непрерывно зависит от входных данных, т.е. малому изменению входных
данных соответствует малое изменение решения. Устойчивость характеризу-
ет чувствительность разностной схемы к различного рода погрешностям, она
является внутренним свойством разностной задачи, и это свойство не связы-
вается непосредственно с исходной дифференциальной задачей ( отличие от
сходимости и аппроксимации).
Ограничимся описанием явных схем, которые являются наиболее про-
стыми, и их реализация на современн
ых быстродействующих ЭВМ не вызы-
вает затруднений.
Построим разностную схему для решения смешанной краевой задачи
нестационарной теплопроводности для неоднородного уравнения
335
315
295
275
T,K
0 5 10
,c
точное решение
метод Швеца
