Гордин Р.К. Геометрия. Планиметрия. 7-9 классы

Подождите немного. Документ загружается.

§ 3.3. Теорема синусов 161

Задачи второго уровня

3.118. Дан треугольник ABC, в котором ∠A =

, ∠B =

. На стороне AB взята точка D, а на стороне AC — точ-

ка M, причем CD — биссектриса треугольника ABC, DM k BC

и AM = a. Найдите CM .

3.119. Углы треугольника равны

, и , а периметр ра-

вен P . Найдите стороны треугольника.

3.120. Одна из боковых сторон трапеции образует с б´оль-

шим основанием угол

, а вторая равна a и образует с меньшим

основанием угол

. Найдите среднюю линию трапеции, если

меньшее основание равно b.

3.121. В окружности радиуса 12 хорда AB равна 6, а хор-

да BC равна 4. Найдите хорду, соединяющую концы дуги AC.

3.122. Основания трапеции равны 4 и 16. Найдите радиу-

сы окружностей, вписанной в трапецию и описанной около нее,

если известно, что эти окружности су ществуют.

3.123. На стороне AB треугольника ABC во внешнюю сто-

рону построен равносторонний треугольник. Найдите расстоя-

ние между его центром и вершиной C, если AB = c и ∠C = 120

◦

3.124. Стороны треугольника равны 1 и 2, а угол между

ними равен 60

◦

. Через центр вписанной окружности этого тре-

угольника и концы третьей стороны проведена окружность.

Найдите ее радиус.

3.125. Докажите, что если стороны a, b и противолежащие

им углы

и треугольника связаны соотношением

cos

то треугольник равнобедренный.

3.126. Две стороны треугольника равны a и b. Найдите тре-

тью сторону треугольника, если его угол, лежащий против тре-

тьей стороны, в два раза больше угла, лежащего против сторо-

ны, равной b.

3.127. Две окружности пересекаются в точках A и B. Пря-

мая, проходящая через точку A, вторично пересекает эти

окружности в точках C и D, причем точка A лежит меж-

ду C и D, а хорды AC и AD пропорциональны радиусам своих

окружностей. Докажите, что биссектрисы углов ADB и ACB

пересекаются на отрезке AB.

162 9 класс

3.128. В окружность вписаны две трапеции с соответствен-

но параллельными сторонами. Докажите, что диагональ одной

из них равна диагонали другой трапеции.

3.129. Докажите, что для любого треугольника проекция

диаметра описанной окружности, перпендикулярного одной

стороне треугольника, на прямую, содержащую вторую сторону,

равна третьей стороне.

3.130. Каждое из оснований высот треугольника проециру-

ется на его стороны. Докажите, что длина отрезка, соединяю-

щего проекции, не зависит от выбора высоты.

3.131. На окружности, описанной около треугольника ABC,

найдите точку M такую, что расстояние между ее проекциями

на прямые AC и BC максимально.

3.132. Высоты треугольника ABC пересекаются в точке H.

Докажите, что радиусы окружностей, описанных около тре-

угольников ABC, AHB, BHC и AHC, равны между собой.

3.133. В окружности проведены две хорды AB = a и AC =

= b. Длина ду ги AC вдвое больше длины дуги AB. Найдите

радиус окружности.

3.134. Из точки M на окружности проведены три хорды:

MN = 1, MP = 6, M Q = 2. При этом углы NMP и P MQ

равны. Найдите радиус окружности.

3.135. В треугольнике ABC известно, что AB = 2, AC = 5,

BC = 6. Найдите расстояние от вершины B до точки пересече-

ния высот треугольника ABC.

3.136. В остроугольном треугольнике ABC из вершин A и C

опущены высоты AP и CQ на стороны BC и AB. Известно,

что площадь треугольника ABC равна 18, площадь треуголь-

ника BP Q равна 2, а P Q = 2

√

2. Найдите радиус окружности,

описанной около треугольника ABC.

3.137. Отрезки AB и CD — диаметры одной окружности.

Из точки M этой окружности опущены перпендикуляры M P

и MQ на прямые AB и CD. Докажите, что длина отрезка P Q

не зависит от положения точки M.

3.138. Постройте треугольник по углу и радиусам вписан-

ной и описанной окружностей.

3.139. Через вершины A и B треугольника ABC проходит

§ 3.3. Теорема синусов 163

окружность радиуса r, пересекающая сторону BC в точке D.

Найдите радиус окружности, проходящей через точки A, D и C,

если AB = c и AC = b.

3.140. Угол при основании равнобедренного треугольника

равен . Найдите отношение радиуса вписанной в данный тре-

угольник окружности к радиусу описанной около него окруж-

ности.

3.141. Радиус окружности, описанной около остроугольного

треугольника ABC, равен 1. Известно, что на этой окружности

лежит центр другой окружности, проходящей через вершины A,

C и точку пересечения высот треугольника ABC. Найдите AC.

3.142. Дан треугольник ABC, в котором ∠BAC = 75

◦

AB = 1, AC =

√

6. На стороне BC выбрана точка M так,

что ∠BAM = 30

◦

. Прямая AM пересекает окружность, опи-

санную около треугольника ABC, в точке N, отличной от A.

Найдите AN.

3.143. Даны отрезок AB и на нем точка C. Найдите геомет-

рическое место точек пересечения двух равных окружностей,

одна из которых проходит через точки A и C, другая — через

точки C и B.

3.144. Продолжения высот AM и CN остроугольного тре-

угольника ABC пересекают описанную около него окружность

в точках P и Q. Найдите радиус описанной окружности, ес-

ли AC = a, P Q =

3.145. Отрезки, соединяющие основания высот остроуголь-

ного треугольника, равны 8, 15 и 17. Найдите радиус окружно-

сти, описанной около треугольника.

3.146. Две окружности радиусов R и r пересекаются в точ-

ках A и B и касаются прямой в точках C и D. N — точка пере-

сечения прямых AB и CD (B между A и N). Найдите радиус

окружности, описанной около треугольника ACD, и отношение

высот треугольников NAC и NAD, опущенных из вершины N.

3.147. В треугольник ABC помещены три равных окруж-

ности, каждая из которых касается двух сторон треугольника.

Все три окружности имеют одну общую точку. Найдите ради-

усы этих окружностей, если радиусы описанной и вписанной

окружностей треугольника ABC равны R и r.

164 9 класс

3.148. В выпуклом четырехугольнике ABKC сторона AB =

√

3, диагональ BC равна 1, а углы ABC, BKA и BKC рав-

ны 120

◦

, 30

◦

и 60

◦

соответственно. Найдите сторону BK.

3.149. В треугольнике ABC известно, что AB = 20, AC =

= 24. Известно также, что вершина C, центр вписанной в тре-

угольник ABC окружности и точка пересечения биссектрисы

угла A со стороной BC лежат на окружности, центр которой

расположен на стороне AC. Найдите радиус описанной около

треугольника ABC окружности.

Задачи третьего уровня

3.150. В выпуклом четырехугольнике ABCD проведены

диагонали AC и BD. Известно, что AD = 2, ∠ABD = ∠ACD =

= 90

◦

и расстояние между центрами окружностей, вписанных в

треугольники ABD и ACD, равно

√

2. Найдите BC.

3.151. Постройте треугольник по двум сторонам так, чтобы

медиана, проведенная к третьей стороне, делила угол треуголь-

ника в отношении 1 : 2.

3.152. Диагональ AC квадрата ABCD совпадает с гипоте-

нузой прямоугольного треугольника ACK, причем точки B и K

лежат по одну сторону от прямой AC. Докажите, что BK =

|AK−CK|

√

и DK =

AK+CK

√

3.153. На окружности, описанной около треугольника ABC,

взята точка M. Прямая MA пересекается с прямой BC в точ-

ке L, а прямая CM — с прямой AB в точке K. Известно,

что AL = a, BK = b, CK = c. Найдите BL.

3.154. В треугольнике ABC угол ABC равен , угол BCA

равен 2

. Окружность, проходящая через точки A, C и центр

описанной около треугольника ABC окружности, пересекает

сторону AB в точке M. Найдите отношение AM : AB.

§ 3.4. Площадь

Пусть a, b, c — стороны треугольника;

, , — противолежа-

щие им углы; h

— высота, проведенная к прямой, содержащей

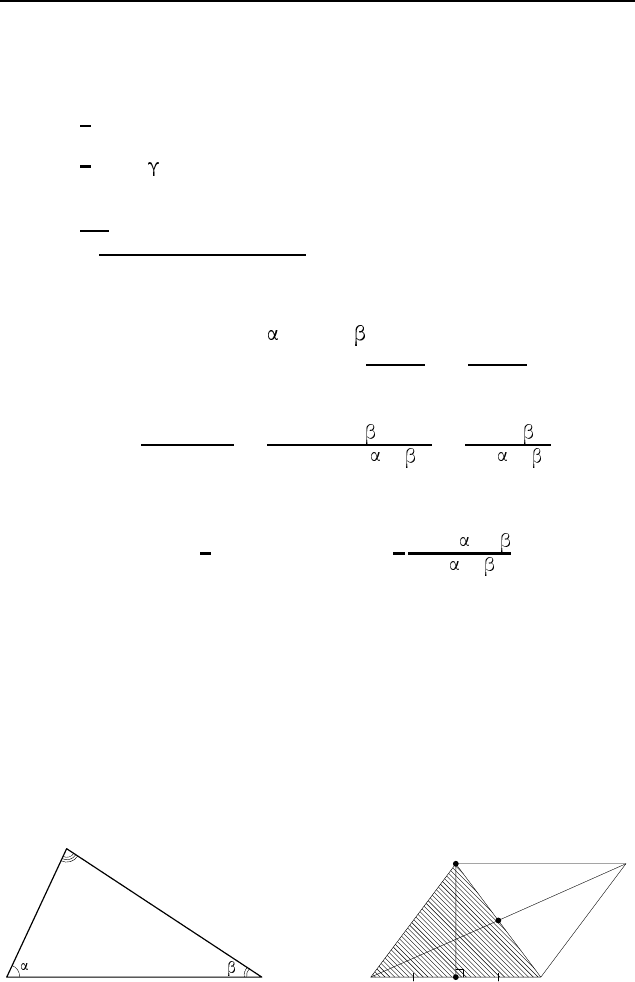
§ 3.4. Площадь 165

сторону a; R — радиус описанной окружности; r — радиус впи-

санной окружности; p — полупериметр.

Формулы площади треугольника:

S =

ab sin

S = pr,

S =

abc

S =

p(p − a)(p − b)(p − c) (формула Герона).

Пример 1. Найдите площадь треугольника ABC, если из-

вестно, что AB = a, ∠A =

, ∠B = .

Решение. По теореме синусов

sin ∠B

sin ∠C

(рис. 77),

откуда

AC =

AB sin ∠B

sin ∠C

a sin

sin(180

◦

− ( + ))

a sin

sin( + )

Следовательно,

ABC

AB · AC sin ∠A =

sin

sin( + )

Пример 2. Две стороны треугольника равны 10 и 12, а ме-

диана, проведенная к третьей, равна 5. Найдите площадь тре-

угольника.

Решение. Пусть AM — медиана треугольника ABC, при-

чем AM = 5, AB = 10, AC = 12 (рис. 78). На продолжении

медианы AM за точку M отложим отрезок MD, равный AM.

Тогда ABDC — параллелограмм с диагоналями BC и AD, а

A B

Рис. 77

Рис. 78

166 9 класс

площадь треугольника ABC равна площади равнобедренного

треугольника ABD, в котором AB = AD = 10, BD = 12. Вы-

соту AH треугольника ABD находим по теореме Пифагора из

прямоугольного треугольника ABH:

AH =

−BH

√

100 − 36 = 8.

Следовательно,

ABC

= S

ABD

BD ·AH =

· 12 · 8 = 48.

Пример 3. Докажите, что площадь выпуклого четырех-

угольника равна половине произведения диагоналей на синус

угла между ними.

Решение. Рассмотрим выпуклый четырехугольник ABCD,

диагонали AC и BD которого пересекаются в точке O (рис. 79).

Пусть ∠AOB =

. Через вершины A и C проведем прямые,

параллельные диагонали BD, а через вершины B и D — пря-

мые, параллельные диагонали AC. Проведенные прямые при

пересечении образуют параллелограмм с углом

при вершине.

Его площадь равна AC · BD sin

, а площадь четырехугольни-

ка ABCD вдвое меньше, т. е. равна

AC · BD sin

Заметим, что доказанная формула верна также для невы-

пуклого четырехугольника.

Пример 4. Вершины ромба расположены на сторонах па-

раллелограмма, а стороны ромба параллельны диагоналям па-

раллелограмма. Найдите отношение площадей ромба и парал-

лелограмма, если отношение диагоналей параллелограмма рав-

но k.

Рис. 79

B C

Рис. 80

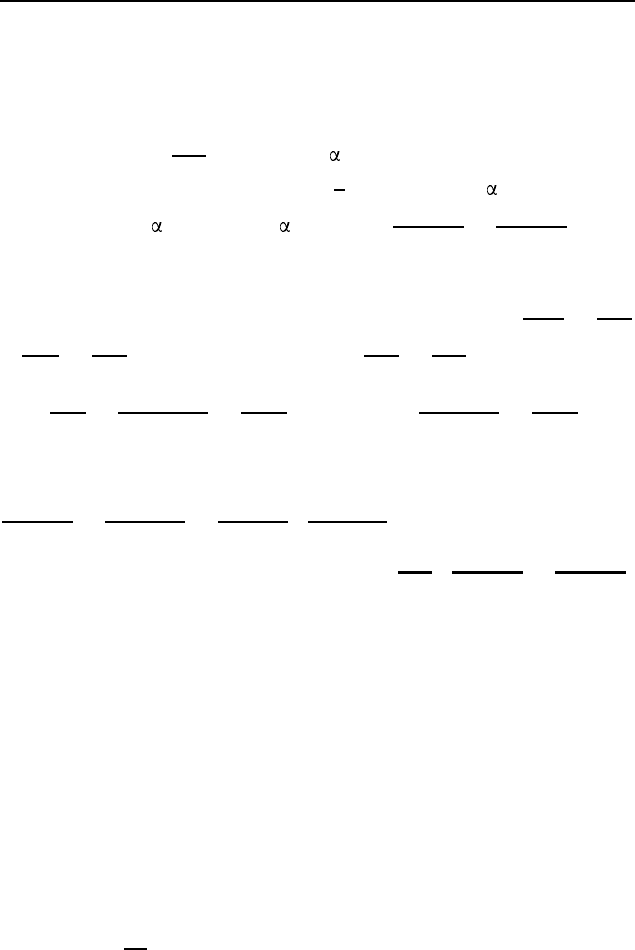
§ 3.4. Площадь 167

Решение. Пусть вершины M , N, K и L ромба MNKL

расположены соответственно на сторонах AB, BC, CD и AD

параллелограмма ABCD (рис. 80), а стороны MN и KN ромба

соответственно параллельны диагоналям AC и BD параллело-

грамма, причем

= k. Если

— угол между диагоналями

параллелограмма, то S

ABCD

AC · BD · sin

и S

KLMN

= M N · KL sin

= M N

sin , поэтому

KLM N

ABCD

2MN

AC·BD

Заметим, что центр ромба совпадает с центром O парал-

лелограмма. Треугольник BMN подобен треугольнику BAC,

а треугольник CKN — треугольнику CDB, поэтому

. Отсюда находим, что

, значит,

BD + AC

1 + k

и MN =

AC · BN

1 + k

Следовательно,

KLM N

ABCD

2MN

AC · BD

2AC

(1 + k)

AC · BD

= 2 ·

(1 + k)

Задачи первого уровня

3.155. Среди всех треугольников с заданными сторона-

ми AB и AC найдите тот, у которого наибольшая площадь.

3.156. Катеты прямоугольного треугольника равны 15 и 8.

Найдите высоту, опущенную на гипотенузу.

3.157. В параллелограмме ABCD угол BAD равен 60

◦

, а

сторона AB равна 3. Биссектриса угла A пересекает сторону BC

в точке E. Найдите площадь треугольника ABE.

3.158. Докажите, что если диагонали выпуклого четырех-

угольника равны, то его площадь равна произведению отрезков,

соединяющих середины противоположных сторон.

3.159. Найдите площадь треугольника, если две его стороны

равны 1 и

√

15, а медиана, проведенная к третьей, равна 2.

3.160. Стороны треугольника равны a, b, b. Найдите высоту,

проведенную к стороне, равной b.

168 9 класс

3.161. В треугольник со сторонами a и b и углом между

ними вписана полуокружность с диаметром на третьей стороне.

Найдите ее радиус.

3.162. а) В треугольнике ABC известно, что AB = 8, AC =

= 6, ∠BAC = 60

◦

. Найдите биссектрису AM.

б) Стороны треугольника равны a и b, а угол между ними

равен . Найдите биссектрису, проведенную из вершины это-

го угла.

3.163. Найдите площадь трапеции:

а) с основаниями 18 и 13 и боковыми сторонами 3 и 4;

б) с основаниями 16 и 44 и боковыми сторонами 17 и 25.

3.164. В треугольнике ABC известно, что ∠BAC =

∠BCA =

, AB = c. Найдите площадь треугольника ABC.

3.165. Найдите площадь трапеции:

а) с основаниями 11 и 4 и диагоналями 9 и 12;

б) с основаниями 6 и 3 и диагоналями 7 и 8.

3.166. В равнобокой трапеции основания равны 40 и 24, а

ее диагонали взаимно перпендикулярны. Найдите площадь тра-

пеции.

3.167. Площадь треугольника ABC равна S, ∠BAC =

AC = b. Найдите BC.

3.168. Две стороны треугольника равны 2

√

2 и 3, площадь

треугольника равна 3. Найдите третью сторону.

3.169. Медианы AN и BM треугольника ABC равны 6 и 9

соответственно и пересекаются в точке K, причем угол AKB

равен 30

◦

. Найдите площадь треугольника ABC.

3.170. Расстояния от точки M, лежащей внутри треуголь-

ника ABC, до его сторон AC и BC соответственно равны 2 и 4.

Найдите расстояние от точки M до прямой AB, если AB = 10,

BC = 17, AC = 21.

3.171. В треугольник вписана окружность радиуса 4. Од-

на из сторон треугольника разделена точкой касания на части,

равные 6 и 8. Найдите две другие стороны треугольника.

3.172. Вершины треугольника соединены с центром вписан-

ной окружности. Проведенными отрезками треугольник разде-

лился на три части, площади которых: 28, 60 и 80. Найдите

стороны треугольника.

§ 3.4. Площадь 169

Задачи второго уровня

3.173. Основание равнобедренного треугольника равно a, а

высота, опущенная на боковую сторону, равна h. Найдите пло-

щадь треугольника.

3.174. Углы треугольника равны

, и , а площадь рав-

на S. Найдите высоты треугольника.

3.175. Углы треугольника равны , и , а площадь рав-

на S. Найдите стороны треугольника.

3.176

. Точки B

и C

— основания высот BB

и CC

тре-

угольника ABC, площадь которого равна S, а угол BAC ра-

вен . Найдите площадь треугольника AB

3.177. Найдите площадь треугольника, если две его стороны

равны 35 и 14, а биссектриса угла между ними равна 12.

3.178. Диагонали трапеции равны 3 и 5, а отрезок, соединя-

ющий середины оснований, равен 2. Найдите площадь трапеции.

3.179. Дан треугольник ABC. Из вершины A проведена

медиана AM, а из вершины B — медиана BP . Известно,

что ∠AP B = ∠BMA, cos ∠ACB = 0,8 и BP = 1. Найдите

площадь треугольника ABC.

3.180. В трапеции ABCD диагонали AC и BD взаимно пер-

пендикулярны, ∠BAC = ∠CDB. Продолжения боковых сто-

рон AB и DC пересекаются в точке K, образуя угол AKD,

равный 30

◦

. Найдите площадь треугольника AKD, если пло-

щадь трапеции равна P .

3.181. В параллелограмме ABCD точка E делит пополам

сторону CD, биссектриса угла ABC пересекает в точке O от-

резок AE. Найдите площадь четырехугольника OBCE, зная,

что AD = a, DE = b, ∠ABO =

3.182. Диагонали трапеции взаимно перпендикулярны. Од-

на из них равна 6. Отрезок, соединяющий середины оснований,

равен 4,5. Найдите площадь трапеции.

3.183. Около окружности радиуса R описан параллело-

грамм. Площадь четырехугольника с вершинами в точках

касания окружности и параллелограмма равна S. Найдите

стороны параллелограмма.

3.184. В треугольнике ABC известно, что AB = 6, BC = 4,

AC = 8. Биссектриса угла C пересекает сторону AB в точке D.

170 9 класс

Через точки A, D и C проведена окружность, пересекающая

сторону BC в точке E. Найдите площадь треугольника ADE.

3.185. В параллелограмме ABCD острый угол BAD ра-

вен

. Пусть O

, O

— центры окружностей, описанных

около треугольников DAB, DAC, DBC, ABC соответственно.

Найдите отношение площади четырехугольника O

площади параллелограмма ABCD.

3.186. В четырехугольнике ABCD острый угол между диа-

гоналями равен

. Через каждую вершину проведена прямая,

перпендикулярная диагонали, не содержащей эту вершину. Най-

дите отношение площади четырехугольника, ограниченного

этими прямыми, к площади четырехугольника ABCD.

3.187. Из точки P , расположенной внутри остроугольного

треугольника ABC, опущены перпендикуляры на его стороны.

Длины сторон и опущенных на них перпендикуляров соответ-

ственно равны a и k, b и m, c и n. Найдите отношение площади

треугольника ABC к площади треугольника, вершинами кото-

рого служат основания перпендикуляров.

3.188. Периметр выпуклого четырехугольника равен 4. До-

кажите, что его площадь не превосходит 1.

3.189. Стороны треугольника не превосходят 1. Докажите,

что его площадь не превосходит

√

3.190. Около треугольника ABC описана окружность. Ме-

диана AD продолжена до пересечения с этой окружностью в

точке E. Известно, что AB + AD = DE, ∠BAD = 60

◦

, AE = 6.

Найдите площадь треугольника ABC.

3.191. Докажите, что в треугольнике ABC:

а)

, где r — радиус вписанной окружности,

а r

, r

и r

— радиусы вневписанных окружностей треуголь-

ника;

б) S =

√

r · r

· r

, где S — площадь треугольника.

3.192. В остроугольном треугольнике ABC проведены вы-

соты AM и CN, O — центр описанной около треугольника ABC

окружности. Известно, что ∠ABC =

, а площадь четырех-

угольника N OMB равна S. Найдите AC.