Гордин Р.К. Геометрия. Планиметрия. 7-9 классы

Подождите немного. Документ загружается.

§ 1.2 181

на сторонах данного угла произвольные точки B и C. Точка

пересечения биссектрис треугольника ABC, проведенных из

вершин B и C, лежит на биссектрисе угла A, так как биссек-

трисы треугольника пересекаются в одной точке. Таким образом

можно найти точку на искомой биссектрисе. А налогично найдем

и вторую точку.

1.74

. Указание. Точка пересечения серединных перпенди-

куляров, проведенных к двум сторонам треугольника, равно-

удалена от всех вершин треугольника, поэтому она лежит на

серединном перпендикуляре к третьей стороне.

1.75. Указание. Существование такой окружности следует

из предыдущей задачи. Если бы существовала еще одна такая

окружность, то ее центр должен был бы лежать на серединном

перпендикуляре к каждой стороне треугольника.

1.76. Указание. Через три точки, не лежащие на одной пря-

мой, проходит единственная окружность.

1.77. Предположим, что ABC — искомый треугольник

(рис. 102), AB — его данная сторона, ∠A — данный угол,

AC + CB — данная сумма сторон. На продолжении отрез-

ка AC за точку C отложим отрезок CB

, равный CB. То-

гда AB

= AC + CB

= AC + CB, а так как CB = CB

то точка C лежит на серединном перпендикуляре к отрез-

ку BB

Треугольник AB

B можно построить (по двум данным сто-

ронам и углу между ними). Пересечение серединного перпенди-

куляра к стороне BB

с отрезком AB

есть искомая вершина C.

1.78. Указание. Пусть ABC — искомый треугольник

(рис. 103), BC и AC — данные стороны, ∠BAC −∠ABC — дан-

ная разность углов (предполагаем, что ∠BAC > ∠ABC). Если

A B

Рис. 102

A B

C C

Рис. 103

182 7 класс

точка C

симметрична вершине C относительно серединного

перпендикуляра к стороне AB, то

∠CAC

= ∠CAB − ∠C

AB = ∠CAB − ∠ABC

и AC

= BC. Следовательно, треугольник CAC

можно постро-

ить по двум сторонам и углу между ними.

1.79. Указание. Точки, симметричные данной вершине от-

носительно данных прямых, лежат на стороне искомого тре-

угольника.

1.80. Указание. Если две окружности пересекаются в двух

точках, то прямая, проходящая через эти точки, перпендику-

лярна прямой, проходящей через центры окружностей.

1.81

. Указание. Предположим, что задача решена. Пусть

AB и BC — данные стороны, BM — данная медиана (рис. 104).

Отложим на продолжении медианы BM за точку M отре-

зок MP , равный BM . Тогда P C = AB. Треугольник BP C

строим по трем сторонам. Продолжив его медиану CM за

точку M на отрезок MA, равный MC, получим вершину A

искомого треугольника.

1.82. На продолжении отрезка A

за точку C

возьмем

точку M (рис. 105). Тогда

∠AC

M = ∠BC

= ∠AC

т. е. C

A — биссектриса угла B

M. Поэтому точка A равно-

удалена от сторон этого угла. Если N — точка на продолже-

нии A

за точку B

, то аналогично докажем, что точка A

равноудалена от сторон угла N B

. Следовательно, точка A

B C

A P

Рис. 104

B CA

Рис. 105

§ 1.3 183

Рис. 106

равноудалена от сторон угла MA

N, т. е. лежит на биссектрисе

этого у гла. Поэтому

∠AA

C = ∠AA

+ ∠B

C = ∠AA

+ ∠C

B = ∠AA

т. е. AA

⊥ BC.

1.83. Пусть AE, BD и CM — биссектрисы треугольни-

ка ABC и ∠ABC = 120

◦

. На продолжении стороны AB за

точку B возьмем точку K (рис. 106). Поскольку ∠EBK =

= 180

◦

− ∠ABC = 180

◦

− 120

◦

= 60

◦

= ∠DBE, то BE —

биссектриса угла DBK, смежного с углом ABD. Поэтому точ-

ка E равноудалена от прямых AB, DB и CD. Следовательно,

DE — биссектриса угла BDC. Аналогично, DM — биссектриса

угла ADB. Следовательно,

∠MDE =

(∠ADB + ∠BDC) = 90

◦

§ 1.3

1.89. 30

◦

, 100

◦

, 50

◦

. 1.91. 75

◦

, 65

◦

, 40

◦

. 1.92. 90

◦

, 40

◦

, 50

◦

и 90

◦

, 40

◦

, 50

◦

. 1.94

. Две прямые, параллельные данной.

1.96. Треугольник AMD равнобедренный (рис. 107), поэто-

му ∠MAD = ∠MDA = ∠CAD. Следовательно, M D k AC.

1.98. 7 : 6 : 5.

1.99. Пусть M и N — середины боковых сторон соот-

ветственно AB и AC равнобедренного треугольника ABC

(рис. 108). Тогда AM = AN как половины равных отрезков AB

и AC, поэтому треугольник AM N также равнобедренный, зна-

чит, ∠AMN = 90

◦

−

∠A = ∠ABC. Следовательно, MN k BC.

184 7 класс

Рис. 107

B C

M N

Рис. 108

A CM N

Рис. 109

1.100. 90

◦

. 1.101. 1.

1.103. Пусть , и + — углы треугольника. Тогда + +

+ (

+ ) = 180

◦

, откуда + = 90

◦

1.104. По теореме о внешнем угле треугольника (рис. 109)

∠BMN = ∠ABM + ∠BAC = ∠ACB + ∠CBN = ∠BNM.

1.105. Обозначим ∠A =

, ∠B = ∠C = 2 (рис. 110). То-

гда ∠ABD =

, поэтому AD = BD. Кроме того, ∠BDC = ∠A +

+ ∠ABD = 2

, поэтому BD = BC. Следовательно, AD = BC.

1.106. 50

◦

, 110

◦

, 20

◦

1.107. 37,5

◦

. Указание. AN — биссектриса треугольни-

ка ABC.

1.108. 25

◦

. Указание. Воспользуйтесь равенством ∠BAM =

= ∠BMA = ∠MAC + ∠MCA.

1.109. 36

◦

. Обозначим ∠B = (рис. 111). Тогда ∠BAM =

, ∠AMC = ∠B + ∠BAM = 2 , ∠BAC = ∠BCA = 2 . Из

уравнения

+ 2 + 2 = 180

◦

находим, что = 36

◦

1.110. 36

◦

, 36

◦

, 108

◦

и 72

◦

, 72

◦

, 36

◦

. 1.112. 10

◦

. 1.113. 30

◦

1.114. Да.

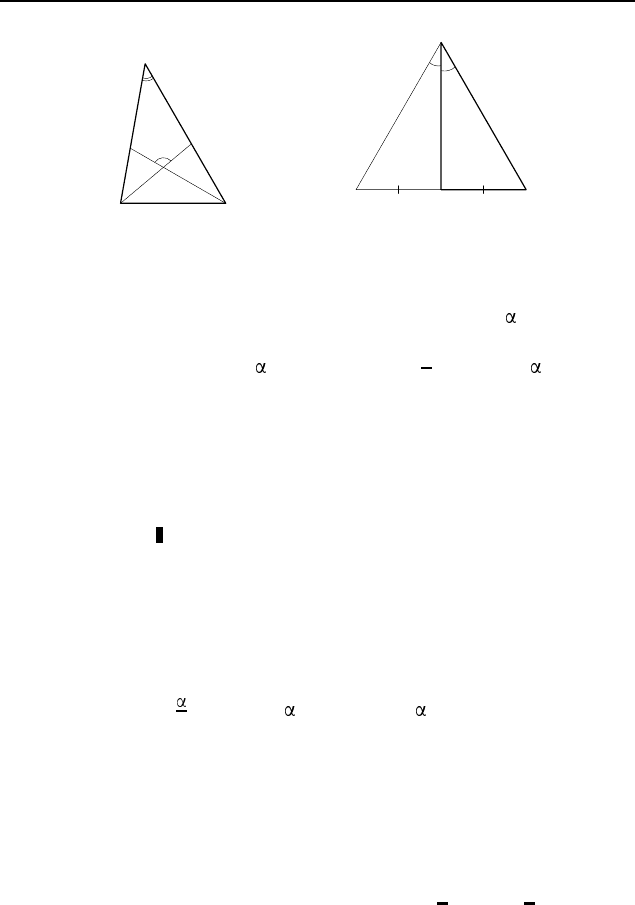
Пусть D — точка на продолжении боковой сто-

роны AB равнобедренного треугольника ABC за вершину A

B C

Рис. 110

A C

Рис. 111

B C

Рис. 112

§ 1.3 185

B C

Рис. 113

BCB

◦

Рис. 114

(рис. 112), а K — точка на биссектрисе угла DAC (внешнего

угла треугольника ABC). Обозначим ∠B = ∠C =

. Тогда

∠DAC = ∠B + ∠C = 2 , ∠CAK =

∠DAC =

= ∠C,

следовательно, AK k BC. Пусть теперь AK k BC. Докажем,

что треугольник ABC равнобедренный. Действительно,

∠B = ∠ABC = ∠DAK = ∠CAK = ∠ACB = ∠C.

1.115. 40

◦

Пусть биссектрисы, проведенные из вершин B

и C треугольника ABC, пересекаются в точке K и ∠BKC =

= 110

◦

(рис. 113). Тогда ∠KBC + ∠KCB = 180

◦

− 110

◦

= 70

◦

∠ABC + ∠ACB = 2(∠KBC + ∠KCB) = 140

◦

. Следовательно,

∠A = 180

◦

− (∠ABC + ∠ACB) = 180

◦

− 140

◦

= 40

◦

1.116

. 90

◦

. 1.117

или 180

◦

− . 1.118. 40

◦

1.119. Нет. Указание. Каждая сторона треугольника видна

из точки пересечения биссектрис под тупым углом (см. зада-

чу 1.116

1.120

. На продолжении катета BC, лежащего против угла

в 30

◦

в прямоугольном треугольнике ABC, отложим вне тре-

угольника отрезок B

C, равный BC (рис. 114). Тогда треуголь-

ник ABB

равносторонний, поэтому BC =

AB.

1.121

. На продолжении указанного катета BC за верши-

ну C прямого угла треугольника ABC отложим отрезок CB

равный BC (рис. 114). Тогда треугольник ABB

равносторон-

ний, ∠B = 60

◦

, ∠BAC = 90

◦

− ∠B = 30

◦

186 7 класс

A CE

Рис. 115

A B

Рис. 116

B C

Рис. 117

1.122. 2 и 6.

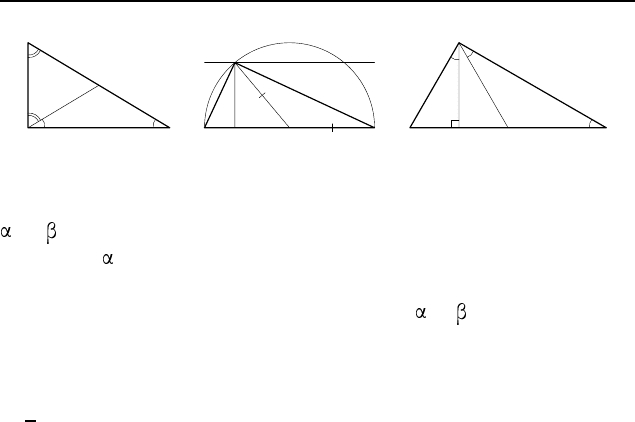
1.123. Пусть указанный перпендикуляр пересекает пря-

мую AB в точке F (рис. 115). Тогда DF = DE, так как

биссектриса AD равнобедренного треугольника AF E явля-

ется его медианой. Поскольку ∠F BD = 180

◦

− 108

◦

= 72

◦

и ∠AF D = 90

◦

− ∠DAF = 90

◦

− 18

◦

= 72

◦

, треугольник BDF

равнобедренный. Следовательно, BD = DF = DE.

1.124. Пусть биссектрисы AM и BN равностороннего тре-

угольника ABC пересекаются в точке O (рис. 116). Из равенства

прямоугольных треугольников ANO и BM O следует, что OM =

= ON. Поскольку ∠OAN = 30

◦

, то

OM = ON =

AO.

Аналогично для остальных биссектрис.

1.125. 60

◦

, 60

◦

1.126. Пусть AC и BD пересекаются в точке O (рис. 117).

Треугольники ABC и DCB равны по двум сторонам и углу

между ними, поэтому AC = BD и ∠BAC = ∠BDC, а так как

∠AOB = ∠DOC, то ∠ABO = ∠DCO. Значит, равны треуголь-

ники AOB и DOC, поэтому AO = DO и BO = CO. Углы при

общей вершине O равнобедренных треугольников AOD и BOC

равны, поэтому равны и углы при их основаниях: ∠ACB =

= ∠CAD. Следовательно, AD k BC.

1.130. 30

◦

или 150

◦

1.131. Указание. Вычислите углы ABN и CBN.

1.132. 70

◦

1.133

. Пусть ABC — прямоугольный треугольник с гипо-

тенузой AB (рис. 118). Обозначим ∠A =

, ∠B = . Тогда

§ 1.3 187

Рис. 118

A B

Рис. 119

Рис. 120

+ = 90

◦

. Отметим на гипотенузе такую точку M, что

∠ACM =

. Тогда

∠BCM = ∠ACB − ∠ACM = 90

◦

−

= = ∠CBM.

Так как треугольники ACM и BCM равнобедренные, то AM =

= CM = BM, т. е. CM — медиана треугольника ABC и CM =

AB.

1.134. Предположим, что ABC — искомый треугольник

(рис. 119), AB — его данная гипотенуза, CH — данная высота.

Тогда медиана CM равна половине AB, поэтому вершина C

лежит на окружности с центром M и диаметром AB. С другой

стороны, вершина C удалена от прямой AB на расстояние,

равное данной высоте, значит, точка C лежит на прямой,

параллельной AB и расположенной на расстоянии, равном дан-

ной высоте, от прямой AB. Отсюда вытекает построение тре-

угольника.

1.135. Четверть окружности.

1.136. Пусть CH и CM — высота и медиана прямоугольного

треугольника ABC, проведенные из вершины прямого угла C,

∠A = 30

◦

(рис. 120). Каждый из углов HCB и HAC в сумме с

углом ACH составляют 90

◦

, поэтому ∠HCB = ∠HAC = ∠A =

= 30

◦

. С другой стороны, в равнобедренном треугольнике AMC

(см. задачу 1.133

) углы при основании AC равны, поэтому

∠ACM = ∠CAM = ∠A = 30

◦

. Следовательно,

∠HCM = ∠ACB − ∠HCB − ∠ACM = 90

◦

− 30

◦

− 30

◦

= 30

◦

1.137. Пусть M — середина гипотенузы прямоугольного

треугольника ABC, ∠A = 30

◦

, точка K лежит на катете AC,

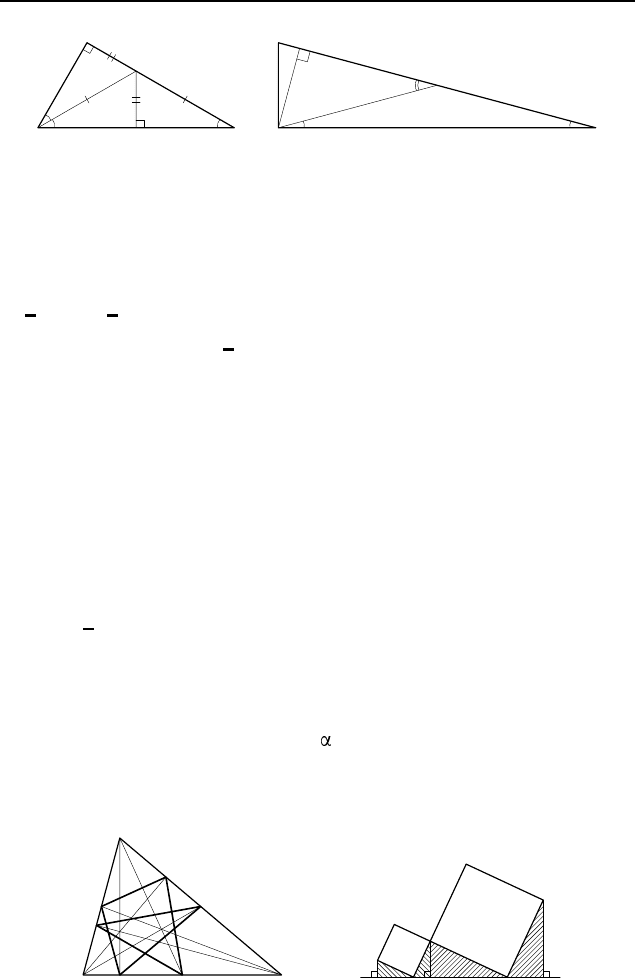
188 7 класс

Рис. 121

Рис. 122

MK ⊥ AB (рис. 121). Тогда BK = AK, ∠CBK = ∠ABC −

−∠ABK = 60

◦

−30

◦

= 30

◦

= ∠KBM. Из равенства прямоуголь-

ных треугольников BCK и BMK следует, что MK = CK =

BK =

AK, поэтому AC = CK + AK = CK + 2CK = 3CK.

Значит, MK = CK =

AC.

1.138. Пусть CH — высота прямоугольного треугольни-

ка ABC, проведенная из вершины прямого угла C, ∠A =

= 15

◦

(рис. 122). Проведем медиану CM. Тогда ∠CMH —

внешний угол равнобедренного треугольника AMC, поэто-

му ∠CMH = 30

◦

. Из прямоугольного треугольника CMH

находим, что CM = 2CH = 2. Следовательно, AB = 2AM =

= 2CM = 4.

1.139. Указание. B

— медиана прямоугольного треуголь-

ника BB

C, проведенная к гипотенузе BC, поэтому

BC (рис. 123).

1.140. Указание. Пусть CH — высота прямоугольного тре-

угольника ABC (рис. 124). Тогда треугольник AME равен тре-

угольнику CHA, а треугольник F N B — треугольнику BHC.

1.141. Обозначим ∠BAC =

(рис. 125). Из равенства пря-

моугольных треугольников ABC и DKC (по двум катетам)

B C

Рис. 123

M A H B N

Рис. 124

§ 1.3 189

следует, что ∠CDK = ∠BAC = . Пусть

A H B

Рис. 125

прямая CP пересекает отрезок AB в

точке H. Поскольку CP — медиана

прямоугольного треугольника DKC,

проведенная из вершины прямого угла,

∠ACH = ∠KCP = ∠CKD = 90

◦

−

Следовательно,

∠AHC = 180

◦

− ∠ACH − ∠CAH = 180

◦

− (90

◦

− ) − = 90

◦

1.143. а) 60

◦

< 180

◦

; б) 0

◦

< 6 60

◦

; в) 0

◦

< < 90

◦

1.144

. а) 360

◦

; б) 540

◦

; в) 180

◦

(n − 2).

1.145. 180

◦

1.146. У девятиугольника

9·6

= 27 диагоналей. Через про-

извольную точку проведем 27 прямых, соответственно парал-

лельных этим диагоналям. Получим 54 угла. Если каждый из

них не меньше 7

◦

, то их сумма не меньше 54 · 7

◦

= 378

◦

> 360

◦

что невозможно.

1.147. 360

◦

. 1.148. 135

◦

. 1.149. 45

◦

1.150. Указание. Пусть искомая точка B построена, BC —

перпендикуляр, опущенный из точки B на вторую сторону угла,

O — вершина данного угла, AB = BC (рис. 126). Предположим,

что точка B лежит на отрезке OA. Тогда угол BAC при основа-

нии равнобедренного треугольника ABC равен половине внеш-

него угла OBC, который дополняет данный угол до прямого.

Аналогично для случая, когда точка B лежит вне отрезка OA.

1.151

. Предположим, что треугольник ABC построен

(рис. 127). Пусть BC = a — данная сторона, ∠A =

— данный

угол, AB + AC = d — данная сумма сторон. На продолжении

O C

Рис. 126

Рис. 127

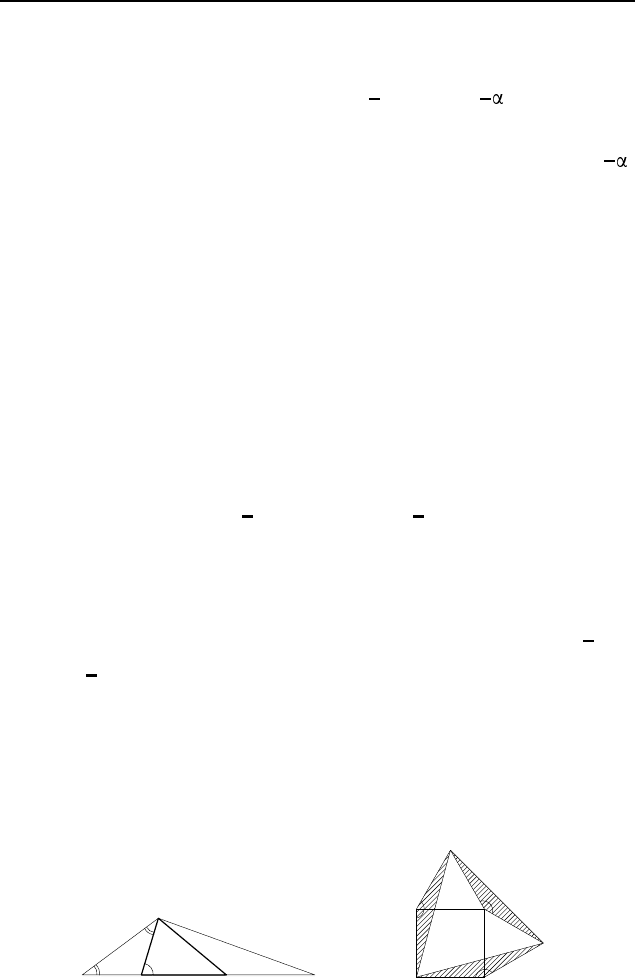
190 7 класс

стороны BA за точку A отложим отрезок AD, равный AC.

Тогда BD = BA + AD = BA + AC = d, треугольник DAC

равнобедренный. Поэтому ∠BDC =

∠BAC =

Отсюда вытекает следующее построение. Строим отре-

зок BD, равный d. От луча DB откладываем угол, равный

С центром в точке B проводим окружность радиуса a. Точка пе-

ресечения этой окружности с проведенным ранее лучом (таких

точек может быть две) есть искомая вершина C. Пересечение

серединного перпендикуляра к отрезку DC с прямой BD дает

искомую вершину A.

1.152. Предположим, что треугольник ABC построен, ∠A и

∠B — данные углы, P — данный периметр (рис. 128). На про-

должении отрезка AB за точку B отложим отрезок BB

, рав-

ный BC, а на продолжении отрезка AB за точку A — отре-

зок AA

, равный AC. Треугольники A

AC и B

BC — равно-

бедренные. Поэтому

∠A

∠A, ∠B

∠B,

= A

A + AB + BB

= AC + AB + BC = P.

Треугольник, равный треугольнику A

C, строим по стороне

(равной P ) и двум прилежащим к ней углам (∠A

∠A,

∠B

∠B). Серединные перпендикуляры к сторонам A

и B

C пересекают отрезок A

в искомых вершинах A и B.

1.153. Так как AB = BK = CK = CL, то

∠ABK = ∠ABC + ∠CBK = 90

◦

+ 60

◦

= 150

◦

A BA

Рис. 128

Рис. 129