Гордин Р.К. Геометрия. Планиметрия. 7-9 классы

Подождите немного. Документ загружается.

§ 1.7 221

P Q

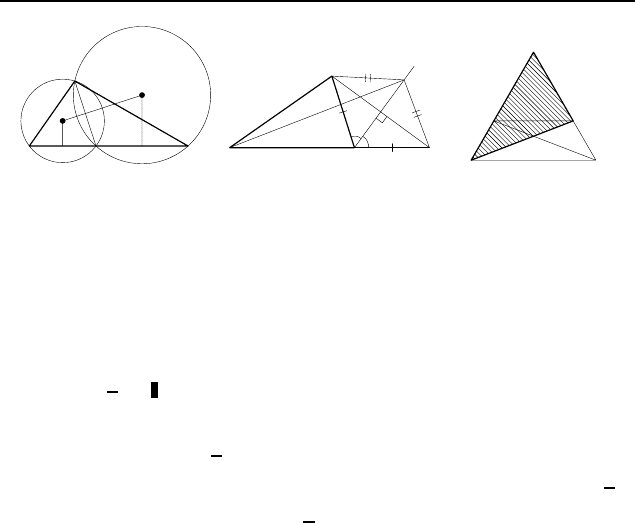
Рис. 204

A C B

Рис. 205

Рис. 206

ка ADC, значит, AD < AC. Если же ∠ADB > 90

◦

, то анало-

гично докажем, что AD < AB.

1.376. Указание. Соедините одну из данных точек с проти-

воположной вершиной треугольника и воспользуйтесь резуль-

татом предыдущей задачи.

1.377.

Проекции центров O

и O

данных окружно-

стей на BC — середины P и Q отрезков BM и MC (рис. 204).

Тогда O

> P Q =

Если AM — высота треугольника BAC, то O

= P Q =

В остальных случаях O

1.378. Пусть B

— точка, симметричная точке B относи-

тельно прямой CM (рис. 205). Поскольку биссектриса есть ось

симметрии угла, точка B

лежит на продолжении стороны AC

за точку C, CB

= CB и MB

= MB. Поэтому

MA + MB = MA + M B

> AB

= CA + CB

= CA + CB.

1.379. Если треугольник ABC равносторонний, то AB +

+ BC = 2BC. Пусть AB 6= AC (рис. 206). При симметрии

относительно биссектрисы угла A вершина C переходит в точ-

ку C

луча AB, а вершина B — в точку B

луча AC. При

этом

= BC, CC

= AC, BB

= AB.

Следовательно,

2BC = BC + B

> BB

+ CC

= AB + AC

(см. задачу 1.351

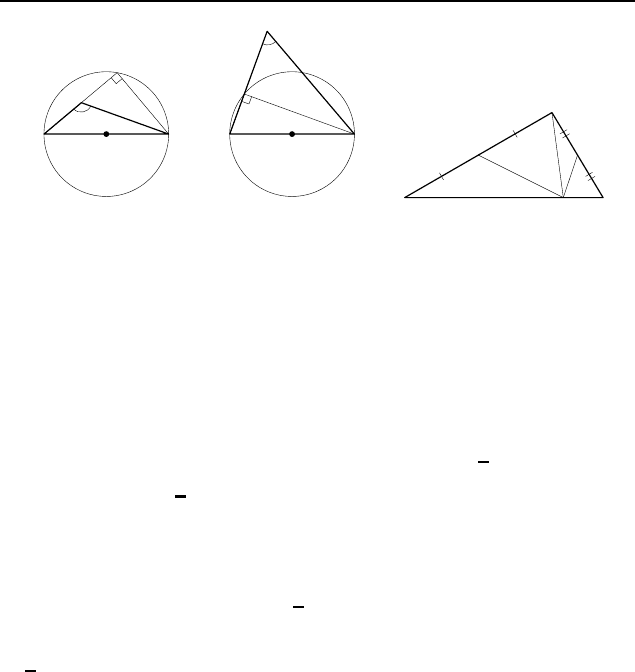
222 7 класс

B C

а)

B C

б )

Рис. 207

C M A

E D

Рис. 208

1.380. Пусть ∠BAC < 90

◦

. Докажем, что точка A лежит

вне окружности с диаметром BC. Ясно, что точка A не мо-

жет лежать на этой окружности, так как тогда ∠BAC = 90

◦

Предположим, что она внутри окружности (рис. 207, а), и про-

должим отрезок BA до пересечения с окружностью в точке M.

Тогда ∠BAC > ∠BMC = 90

◦

, что невозможно. Значит, точка A

лежит вне окружности. Следовательно, AA

BC.

Пусть AA

BC. Тогда точка A лежит вне окружности с

диаметром BC. Если луч AB пересекает окружность в точке M

(рис. 207, б ), то ∠BAC < ∠BMC = 90

◦

1.381. Поскольку M E — медиана треугольника BMC

(рис. 208) и ME > EC =

BC, то угол BMC острый (см.

задачу 1.380). Значит, угол AM B тупой, следовательно, MD <

AB = AD.

1.382. Указание. Постройте окружность на другой диагона-

ли как на диаметре.

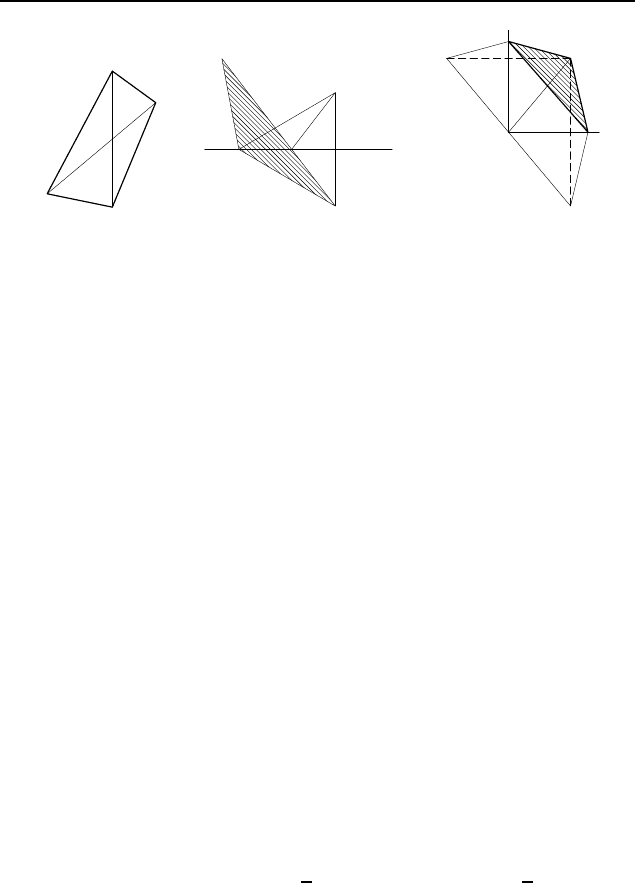
1.383. Пусть M — точка пересечения диагоналей AC и BD

(рис. 209). В треугольниках AMD и AMB сторона AM — об-

щая, DM = MB, а AD < AB. Поэтому ∠AMD < ∠AMB.

Тогда ∠BMC < ∠CMD. В треугольниках BMC и CM D сторо-

на CM общая, DM = MB, а ∠BMC < ∠CMD. Следовательно,

BC < DC.

1.384

. Пусть N

— точка, симметричная точке N относи-

тельно пря мой l (рис. 210). Тогда для любой точки K этой

прямой

MK + NK = MK + N

K > MN

= M P + P N

= M P + P N.

§ 1.7 223

Рис. 209

Рис. 210

Рис. 211

Равенство достигается в случае, когда точка K совпадает с точ-

кой P пересечения прямых l и M N

1.385. Указание. Рассмотрите точки, симметричные точ-

ке M относительно сторон угла.

1.386. Указание. Рассмотрите точки, симметричные точ-

кам M и N относительно сторон данного угла.

1.387. Пусть C

— точка, симметричная точке C относитель-

но прямой OA (рис. 211), а C

симметрична C относительно

прямой OB. Тогда точки C

, O и C

лежат на одной прямой,

так как

∠C

= ∠C

OC + ∠COC

= 2(∠AOC + ∠COB) = 2 · 90

◦

= 180

◦

Следовательно,

AC + BC + AB = AC

+ BC

+ AB > C

= 2OC.

1.388. Пусть B

— точка, симметричная точке B относи-

тельно биссектрисы угла ACB (рис. 212). Тогда BB

= B

Рассмотрим треугольник AB

. В этом треугольнике

∠AB

> ∠AB

B = 180

◦

− ∠CB

B =

= 180

◦

−

(180

◦

− ∠C) = 90

◦

∠C > 90

◦

Следовательно, BB

= A

< AA

1.389. Продолжим BM до пересечения со стороной AC в

точке N (рис. 213). Тогда

AB + AN > BN = BM + MN и MN + NC > M C.

224 7 класс

A B

Рис. 212

B C

Рис. 213

B C

Рис. 214

Сложив почленно эти неравенства, получим

AB + AN + N C + MN > MN + BM + MC,

или

AB + AC + MN > BM + MC + M N.

Отсюда следует, что AB + AC > BM + MC.

1.390. Из предыдущей задачи следует, что для точки M, ле-

жащей внутри треугольника ABC (рис. 214), верны неравенства

MB + MC < AB + AC,

MB + MA < AC + BC,

MA + MC < AB + BC.

Сложив их почленно, получим

2(MA + MB + MC) < 2(AB + BC + AC).

Отсюда следует, что указанная сумма расстояний меньше пе-

риметра треугольника. Применяя неравенство треугольника к

треугольникам AM C, BMC и AMB, получим

AM + MC > AC, BM + MC > BC и AM + MB > AB,

откуда

AM + BM + CM >

(AB + AC + BC).

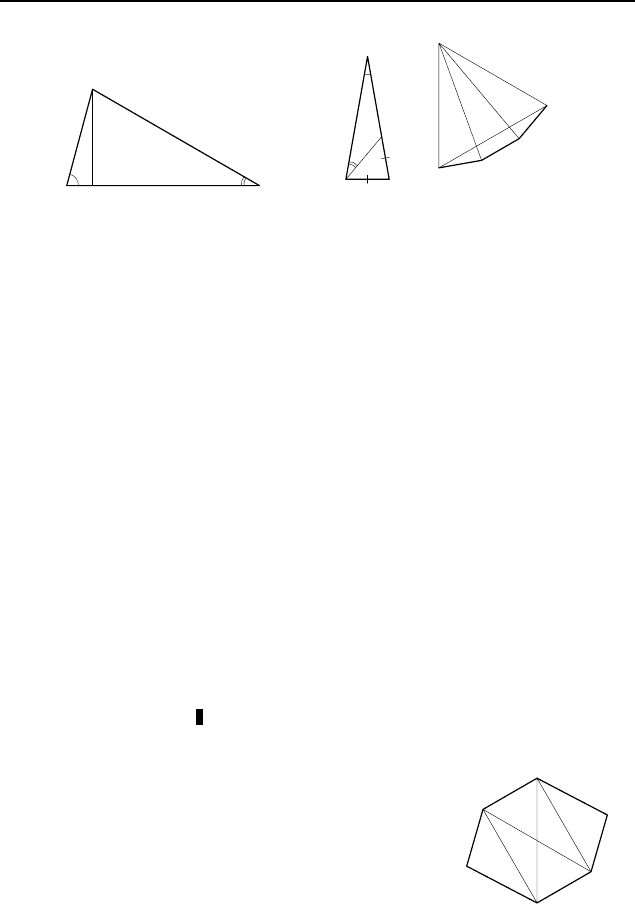
1.391. Пусть в треугольнике ABC угол BAC равен 75

◦

, а

высота BN вдвое меньше стороны AC (рис. 215). Докажем,

что BC = AC. Предположим, что BC < AC. Тогда

∠ABC > 75

◦

, ∠ACB < 30

◦

, BN <

BC <

AC,

§ 1.7 225

A CN

Рис. 215

B C

а)

б )

Рис. 216

что противоречит условию. Аналогично докажем, что BC не

может быть больше AC.

1.392. На боковой стороне AC данного равнобедренного тре-

угольника ABC отложим отрезок CD, равный основанию BC

(рис. 216, а). Тогда ∠ABD = 80

◦

−50

◦

= 30

◦

, значит, в треуголь-

нике ABD угол ABD больше угла BAD, поэтому AD > BD >

> BC (в равнобедренном треугольнике BDC основание BD

лежит против большего угла C). Следовательно,

AC = AD + CD > BC + CD = 2BC.

Пусть точка B

симметрична точке B относительно прямой AC,

а точка B

симметрична C относительно AB

(рис. 216, б ). То-

гда ∠BAB

= 3∠BAC = 60

◦

и AB

= AB, поэтому треуголь-

ник BAB

равносторонний. Следовательно,

AB = BB

< BC + CB

+ B

= 3BC.

1.393. 4 или 5.

У квадрата и правильного пятиугольника

Рис. 217

все диагонали равны. Докажем, что дру-

гих выпуклых многоугольников со всеми

равными диагоналями не существует.

Предположим, что все диагонали вы-

пуклого многоугольника A

. . . A

рав-

ны и n > 6 (рис. 217). Рассмотрим выпук-

лый четырехугольник A

. Сумма

длин его диагоналей A

и A

боль-

ше суммы противоположных сторон A

и A

, что невозможно, так как по предположению эти суммы

равны.

226 7 класс

1.394. Допустим, что в городе P призем-

Рис. 218

лятся, например, 6 самолетов, вылетевших

из городов A

, A

, . . . , A

, и точки A

, . . . , A

— последовательные вершины

шестиугольника (рис. 218). Так как рассто-

яние между городами A

и A

должно быть

больше, чем расстояние от каждого из них

до города P , то ∠A

P A

> 60

◦

(см. зада-

чу 1.143). Аналогично, углы A

P A

, A

P A

, A

P A

, A

P A

больше 60

◦

. Но тогда полный угол при точке P будет

превосходить 360

◦

, что невозможно.

8 класс

§ 2.1

2.1. 3, 9, 3, 9.

2.2. 65

◦

, 115

◦

, 65

◦

, 115

◦

2.3. Указание. Противолежащие стороны AN и MC четы-

рехугольника AMCN равны и параллельны.

2.4. 2a.

2.5. a, a + b, a, a + b или b, a + b, b, a + b.

2.6. 4, 30

◦

, 120

◦

2.8. 2, 4, 2, 4.

2.10

. Указание. Диагонали четырехугольника ABDC пере-

секаются в точке M и делятся ею пополам.

2.13. Пусть AB и CD — различные диаметры окружности

с центром O. Диагонали AB и CD четырехугольника ADBC

пересекаются в точке O, делятся ею пополам и равны между со-

бой как диаметры одной окружности. Следовательно, ADBC —

прямоугольник.

2.14. В точке пересечения диагоналей.

2.15. В точке пересечения диагоналей.

2.16. Указание. Проведите два диаметра под заданным уг-

лом друг к другу.

2.17. 4.

2.18. 4, 8, 4, 8. Указание. Биссектриса угла параллелограм-

ма отсекает от него равнобедренный треугольник.

2.19. 20

◦

, 80

◦

, 80

◦

2.20. Указание. Стороны четырехугольника O

B рав-

ны как радиусы окружностей. Диагонали четырехугольника

AMBN взаимно перпендикулярны и делятся точкой пересече-

ния пополам.

228 8 класс

A B

Рис. 219

B C

Рис. 220

B C

Рис. 221

2.21. Указание. Биссектрисы соседних у глов параллело-

грамма взаимно перпендикулярны.

2.22.

. Указание. Пусть вершина L квадрата CKLM

(рис. 219) лежит на гипотенузе AB равнобедренного прямо-

угольного треугольника ABC, а вершины K и M соответственно

на катетах BC и AC. Тогда AM = ML = MC.

2.23.

. Указание. Пусть вершины L и M квадрата KLMN

лежат на гипотенузе AB равнобедренного прямоугольного тре-

угольника ABC, а вершины K и N соответственно на кате-

тах BC и AC. Тогда BL = KL = M L и AM = MN = M L.

2.24. 12. Указание. Пусть вершины K, L, M и N прямо-

угольника KLMN (рис. 220) расположены соответственно на

сторонах AB, BC, CD и AD квадрата ABCD, KN k BD

и KL k AC, а отрезки KL и MN пересекают диагональ BD

квадрата соответственно в точках P и Q. Тогда KP = BP ,

NQ = DQ, KN = P Q.

2.25. Указание. Пусть ABCD — искомый параллелограмм,

AB, AD и AC — данные стороны и диагональ. Тогда треуголь-

ник ABC можно построить по трем сторонам.

2.26. Указание. Пусть вершина L ромба AKLM (рис. 221)

лежит на стороне BC треугольника ABC, а вершины K и L — на

сторонах AB и AC. Тогда AL — биссектриса треугольника ABC.

2.27. Указание. Пусть окружность с центром O касается

всех сторон ромба ABCD (рис. 222). Если M — точка касания

со стороной AB, то OM ⊥ AB, поэтому

∠MOB = 90

◦

− ∠ABO = 90

◦

−

∠ABC.

2.28. Прямоугольные треугольники ABM и CBN (рис. 223)

§ 2.1 229

Рис. 222

A B

Рис. 223

равны по катету и гипотенузе, поэтому ∠AM B = ∠CNB.

Значит,

∠DMN = 180

◦

− ∠AMB − ∠BMN =

= 180

◦

− ∠CNB − ∠BN M = ∠DNM = 45

◦

= ∠DAC.

Следовательно, M N k AC.

2.29. Пусть M и N — середины противоположных сторон

BC и AD параллелограмма ABCD соответственно (рис. 224),

O — точка пересечения отрезков MN и AC. Треугольни-

ки MOC и NOA равны по стороне и двум прилежащим к

ней углам. Поэтому AO = OC. Следовательно, O — центр

параллелограмма ABCD.

2.30. Пусть ABCDEF — выпуклый шестиугольник, в ко-

тором AB = DE и AB k DE, BC = EF и BC k EF ,

CD = AF и CD k AF (рис. 225). Противолежащие сторо-

ны AB и DE четырехугольника ABDE равны и параллельны,

поэтому ABDE — параллелограмм. Его диагональ AD прохо-

дит через середину O диагонали BE. Аналогично докажем, что

диагональ FC параллелограмма ACDF также проходит через

точку O.

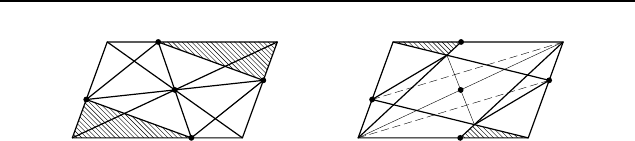
2.31. Пусть O — точка пересечения отрезков AC и NL

(рис. 226). Из равенства треугольников NOC и LOA (по

B C

A D

Рис. 224

Рис. 225

230 8 класс

B C

A D

Рис. 226

B C

A D

Рис. 227

стороне и двум прилежащим к ней углам) следует, что AO = OC

и N O = OL, т. е. диагональ NL четырехугольника KLMN

проходит через центр O параллелограмма ABCD и делится

точкой O пополам. Аналогично докажем, что вторая диаго-

наль MK этого четырехугольника проходит через точку O и

также делится ею пополам. Таким образом, диагонали четы-

рехугольника KLMN пересекаются в точке O и делятся ею

пополам. Следовательно, четырехугольник KLMN — парал-

лелограмм и его центр совпадает с центром O параллелограм-

ма ABCD.

2.32. Указание. Пусть O — центр параллелограмма ABCD

(рис. 226). Докажите, что O — середина отрезков MK и NL.

2.33. Из равенства треугольников ABN и CDL (по двум

сторонам и углу между ними) следует, что ∠ANB = ∠CLD =

= ∠BCL, поэтому AN k CL. Аналогично, BK k DM. Значит,

при пересечении прямых AN , BK, CL и DM получится парал-

лелограмм. Пусть P , Q, R, S — его вершины (рис. 227). Из ра-

венства треугольников BP N и DRL (по стороне и двум приле-

жащим к ней углам) следует, что BP = DR, поэтому P K = MR.

Значит, четырехугольник MP KR — параллелограмм. Его диа-

гональ P R проходит через середину диагонали M K. В то же

время, середина MK совпадает с серединой AC, так как MK

и AC — диагонали параллелограмма AMCK. Следовательно,

P R проходит через середину AC, т. е. через центр параллело-

грамма ABCD. Аналогично для QS.

2.34. Указание. Высоты треугольника ADC пересекаются в

одной точке.

2.35. Пусть M — точка внутри угла ABC (рис. 228). На

продолжении отрезка BM за точку M отложим отрезок MN,