Гордин Р.К. Геометрия. Планиметрия. 7-9 классы

Подождите немного. Документ загружается.

§ 1.5 201

O A

Рис. 155

Рис. 156

Рис. 157

1.233. a. Указание. Примените теорему о равенстве отрезков

касательных, проведенных к окружности из одной точки.

1.234. Указание. Радиус, проведенный в точку касания, пер-

пендикулярен хорде AB.

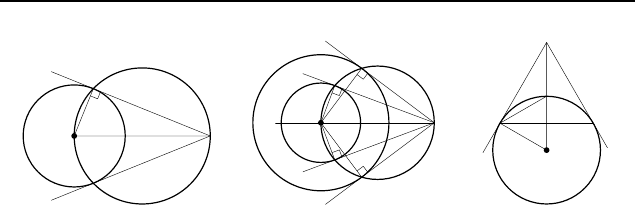
1.235. Указание. ∠ACO = 90

◦

(рис. 155).

1.236. Указание. Отрезок MO виден из точек A, B, C и D

под прямым углом (рис. 156).

1.237

. Указание. Если точка A лежит вне окружности с

центром O, то отрезок AO виден из искомой точки касания под

прямым углом (рис. 155).

1.238. Указание. Центр вписанной в треугольник окружно-

сти лежит на перпендикуляре к стороне треугольника, прове-

денном через точку касания.

1.239. Указание. Через центр данной окружности проведите

прямую, перпендикулярную данной прямой.

1.240. 1 : 3, считая от точки O. Указание. В прямоугольном

треугольнике AMO катет OA равен половине гипотенузы OM

(рис. 157). Если K — середина OM , то треугольник AOK рав-

носторонний.

1.241. 30

◦

, 60

◦

. Указание. Треугольник ADC равносто-

ронний.

1.242. Указание. Геометрическое место середин хорд окруж-

ности, равных данному отрезку, — окружность, концентриче-

ская данной. Далее см. задачу 1.239.

1.243. Указание. Радиус данной окружности, проведенный

в точку D, перпендикулярен данной прямой.

1.244. Указание. Если точки A, B и C лежат на

202 7 класс

окружности, причем AC = BC, то прямая, проходящая через

точку C параллельно AB, — касательная к окружности.

1.245.

(a − c + b),

(a + c − b). Указание. Обозначьте один

из искомых отрезков через x и примените теорему о равен-

стве отрезков касательных, проведенных к окружности из одной

точки.

1.246.

(e −d + c −b + a),

(a −e + d −c + b). Указание. Обо-

значьте один из искомых отрезков через x и примените теорему

о равенстве отрезков касательных, проведенных к окружности

из одной точки.

1.247. 125

◦

. Указание. Треугольник AOD равнобедренный.

1.248. Указание. Треугольник AOD равнобедренный.

1.249. Указание. Центр вписанной окружности треугольни-

ка лежит на биссектрисе данного угла.

1.250. Указание. Искомая точка на прямой удалена от цен-

тра окружности на расстояние, равное гипотенузе прямоуголь-

ного треугольника, один катет которого равен радиусу окруж-

ности, а второй — данному отрезку.

1.251. Указание. Искомая точка принадлежит окружно-

стям, соответственно концентрическим данным.

1.252

. Отрезки касательных, проведенных из одной точ-

Рис. 158

ки к окружности, равны между собой. Точки касания делят

каждую сторону четырехугольника на две части. Обозначим

последовательно их длины, используя од-

ну букву для равных отрезков, начиная

от какой-нибудь из вершин: a, b, b, c, c, d,

d, a (рис. 158). Ясно, что суммы противопо-

ложных сторон состоят из одинаковых сла-

гаемых.

1.253. Указание. Опустите перпендику-

ляры из центра окружности на указанные

хорды.

1.254. Указание. Примените теорему о равенстве отрезков

касательных, проведенных к окружности из одной точки.

1.255.

(b − a).

Сумма периметров отсеченных тре-

угольников равна периметру данного треугольника (рис. 159).

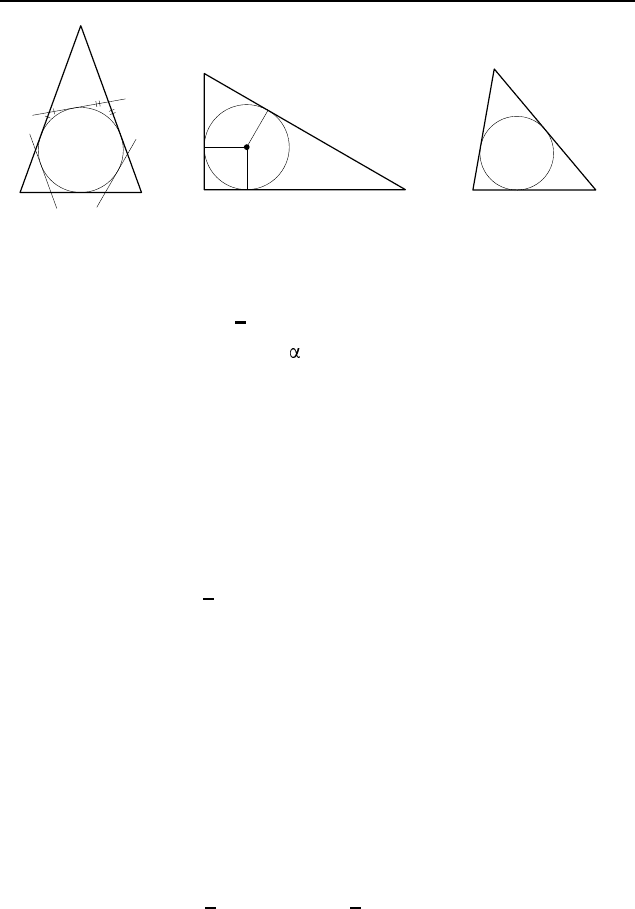
§ 1.5 203

Рис. 159

b − r

a − r

Рис. 160

B C

b − x

c − x

Рис. 161

Поэтому сумма боковых сторон равна b − a. Тогда каждая

боковая сторона равна

(b − a).

1.256. 55

◦

. 1.257. 180

◦

−

1.258

. Обозначим вершины треугольника, противолежа-

щие сторонам a, b, c, через A, B, C соответственно, а точки

касания — через A

, B

, C

(рис. 160). Если O — центр данной

окружности, то OA

— квадрат. Поэтому

= r, BC

= BA

= a − r, AC

= AB

= b −r,

c = AB = AC

+ C

B = a + b − 2r.

Следовательно, r =

(a + b − c).

1.259. Указание. Воспользуйтесь результатом предыдущей

задачи.

1.260

. Обозначим точки касания вписанной окружности со

сторонами BC и AC через K и N соответственно (рис. 161).

Пусть AC = b и AB = c. Тогда

BK = BM = AB − AM = c − x,

CK = CN = AC − AN = b − x,

BC = BK + CK = c − x + b − x = b + c − 2x.

Следовательно, x =

(b + c − a) =

(b + c + a) − a = p − a.

1.261. 1. Указание. Воспользуйтесь результатом зада-

чи 1.260

1.262. 2. Указание. Воспользуйтесь результатом зада-

чи 1.260

204 7 класс

Рис. 162

B C

Рис. 163

1.263

. а) Пусть p — полупериметр треугольника ABC

(рис. 162). Тогда

AN + AP = AB + BN + AC + CP = AB + BM + AC + CM =

= AB + AC + (BM + CM) = AB + AC + BC = 2p

и AN = AP , поэтому AN = p. б) Так как BK = p − AC (см.

задачу 1.260

) и CM = CP = AP −AC = p−AC, то BK = CM.

в) NL = AN − AL = p − (p − BC) = BC.

1.264. 16.

Пусть K — точка касания окружности, вписан-

ной в треугольник ABC (рис. 163), со стороной AB (AB = 10,

AC = 12, BC = 6). Если p — полупериметр треугольника,

то AK = p − BC = 14 − 6 = 8 (см. задачу 1.260

), а AK равно

полупериметру отсеченного треугольника.

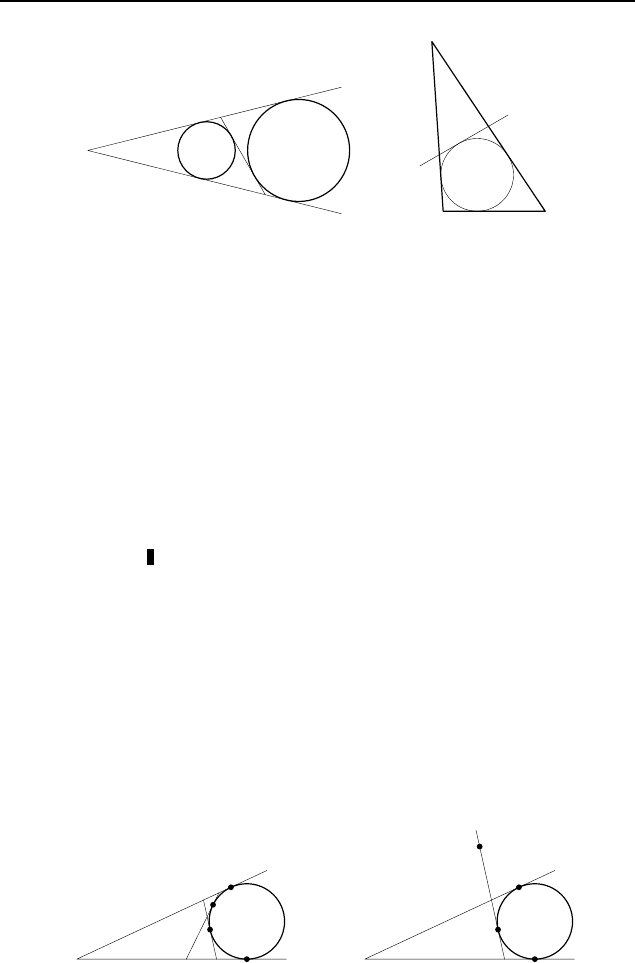
1.265. Пусть M — точка внутри данного угла (рис. 164, а),

A — вершина угла, 2p — данный периметр. Отложим на сторо-

нах данного угла точки B и C так, что AB = AC = p. Впишем

в угол окружность, касающуюся его сторон в точках B и C, и

а)

б )

Рис. 164

§ 1.5 205

R − r

а)

б )

Рис. 165

проведем через точку M касательные к этой окружности (если

это возможно).

Если точка M расположена вне угла (рис. 164, б ), то искомая

прямая — это касательная к построенной окружности, проходя-

щая через точку M и отсекающая от данного угла треугольник,

для которого построенная окружность — вневписанная.

1.266. Указание. Общие внешние (внутренние) касательные

к двум окружностям симметричны друг другу относительно ли-

нии центров.

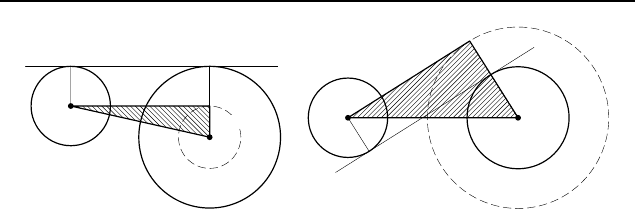
1.267

. Указание. Пусть O

и O

— центры окружностей ра-

диусов R и r. Задача сводится к построению прямоугольного

треугольника по гипотенузе O

и катету R − r (рис. 165, а)

или R + r (рис. 165, б ).

1.268

. Предположим, что точка касания не лежит на линии

центров. Тогда точка, симметричная точке касания относитель-

но линии центров, также принадлежит обеим окружностям, что

противоречит условию.

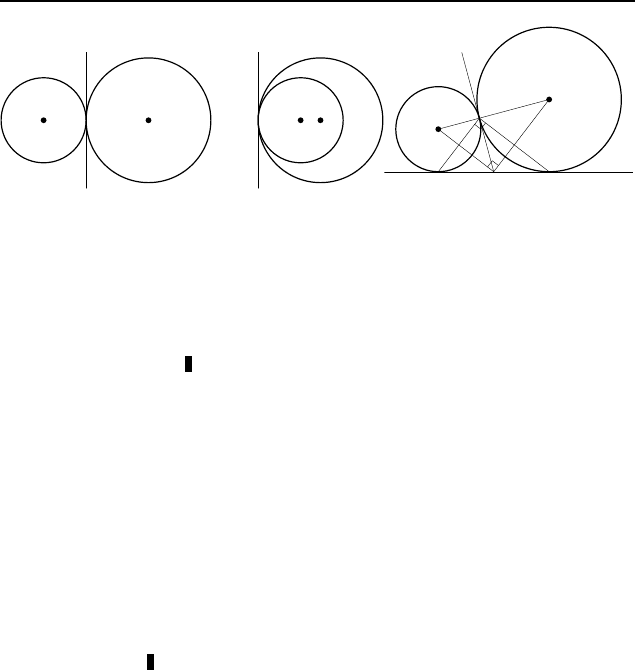
1.269. Пусть M — единственная общая точка окружностей

с центрами O

и O

(рис. 166). Точка M лежит на прямой O

(см. задачу 1.268

). Прямая, проходящая через точку M пер-

пендикулярно O

, является касательной к каждой из окруж-

ностей.

Пусть теперь окружности с центрами O

и O

касаются

некоторой прямой l в точке M. Тогда радиусы O

M и O

перпендикулярны l, значит, точка M лежит на прямой O

Предположим, что окружности имеют еще одну общую точ-

ку K, отличную от M . Тогда точка, симметричная точке K

206 7 класс

Рис. 166

A BM

Рис. 167

относительно прямой O

, также принадлежит обеим окруж-

ностям, что невозможно, так как две различные окружности не

могут иметь три общие точки.

1.270. Верно.

Пусть сумма радиусов r и R двух окружно-

стей равна расстоянию между их центрами O

и O

(рис. 166).

Тогда точка M отрезка O

, удаленная от точки O

на рас-

стояние r, удалена на расстояние R от точки O

, значит, M —

общая точка окружностей. Если K — еще одна общая точка этих

окружностей, то O

< O

K + O

K = r + R, что невозможно.

Остальное аналогично.

1.272. O

— угол между биссектрисами смежных уг-

лов, поэтому ∠O

= 90

◦

(рис. 167). Поскольку M A =

= M K = MB, точка K лежит на окружности с диаметром AB,

следовательно, ∠AKB = 90

◦

1.273. 3r.

Пусть R — радиус большей окружности

(рис. 168). Опустим перпендикуляр из центра меньшей окруж-

ности на радиус большей окружности, проведенный в точку

касания с одной из сторон данного угла. Получим прямо-

угольный треугольник с гипотенузой R + r, катетом R − r и

острым углом, равным 30

◦

, противолежащим этому катету.

Тогда R + r = 2(R − r). Отсюда находим, что R = 3r.

1.274. 1 : 3.

1.275

. Пусть O

и O

— центры окружностей (рис. 169).

Тогда точки O

, O

и A лежат на одной прямой. Треуголь-

ники O

AB и O

AC — равнобедренные, поэтому ∠ABO

= ∠BAO

= ∠CAO

= ∠ACO

, значит, прямая O

B парал-

лельна прямой CO

. Следовательно, параллельны и перпенди-

кулярные к ним касательные.

§ 1.5 207

R − r

r r

Рис. 168

Рис. 169

1.276. Предположим, задача решена. Пусть построенная

окружность с центром O

касается данной прямой l в точке C,

а данной окружности с центром O

— в данной на ней точке A

(рис. 170).

Первый способ. Пусть прямая AC вторично пересекает дан-

ную окружность в точке B. Тогда касательная, проведенная к

этой окружности в точке B, параллельна прямой l, а точки O

и A лежат на одной прямой. Отсюда вытекает следующий

способ построения. Проведем касательную к данной окружно-

сти, параллельную данной прямой l. Пусть B — точка касания, а

прямая AB пересекает прямую l в точке C. Тогда центр O

иско-

мой окружности найдем как точку пересечения перпендикуляра

к прямой l, восставленного из точки C, и прямой O

Второй способ. Пусть касательная к данной окружности,

проведенная через точку A, пересекает данную прямую в точ-

ке M. Тогда искомая окружность касается прямой AM в точ-

ке A, а ее центр O

лежит на биссектрисе угла AMC или на

биссектрисе смежного с ним угла. Отсюда вытекает соответ-

ствующий способ построения.

Рис. 170

208 7 класс

Если данная окружность не имеет с прямой l общих точек

и данная точка не лежит на перпендикуляре к данной прямой,

проходящем через центр данной окружности, задача имеет два

решения (внутреннее и внешнее касания).

1.277. b + p.

Поскольку в четырехугольники ABMQ и

ABNP вписаны окружности (рис. 171), MQ+AB =

и AB+

+ NP =

и P

— периметры этих четырехугольников).

Поэтому

MQ −N P =

− P

) = p.

Отсюда находим, что MQ = NP + p = b + p.

1.278. Обозначим AC

= AB

= x, BA

= BC

= y, CA

= CB

= z, AB = c, AC = b, BC = a (рис. 172). Тогда

x + z = b, x + y = c, z + y = a.

Из полученной системы уравнений находим, что AB

= x =

(b + c − a) = p − a, т. е. точка B

совпадает с точкой каса-

ния вписанной окружности со стороной AC (см. задачу 1.260

Аналогично для точек A

и C

1.279. Указание. Воспользуйтесь результатом задачи 1.278.

1.280. Рассмотрим случай внешнего касания (рис. 173).

Предположим, что окружности S

, S

и S

построены. Пусть S

и S

касаются в точке C, S

и S

— в точке B, S

и S

—

в точке A. Пусть O

, O

и O

— центры окружностей S

, S

и S

соответственно. Тогда точки A, B и C лежат на сторо-

нах треугольника O

, причем O

B = O

C, O

C = O

A = O

B. Из задачи 1.278 следует, что точки A, B и C

Рис. 171

B C

Рис. 172

Рис. 173

§ 1.5 209

являются точками касания вписанной окружности треугольни-

ка O

с его сторонами.

Отсюда вытекает следующий способ построения. Строим

описанную окружность треугольника ABC и проводим к ней

касательные в точках A, B и C. Точки пересечения этих каса-

тельных есть центры искомых окружностей. Если каждая из

двух окружностей, касающихся между собой внешним образом,

внутренне касается третьей окружности, то аналогично можно

доказать, что точки их попарного касания являются точками

касания прямых, содержащих стороны треугольника O

, с

вневписанной окружностью этого треугольника.

1.281

. Пер вый с пособ. Пусть AB + CD = BC + AD и пря-

мые AB и CD пересекаются в точке M. Впишем окружность

в треугольник AMB. Пусть она полностью содержится в че-

тырехугольнике ABCD (рис. 174, а). Докажем, что она касает-

ся BC. Если это не так, то проведем через точку B касательную

к окружности, пересекающую CD в точке C

. Тогда

AB + CD = BC + AD и AB + C

D = BC

+ AD.

Вычитая почленно эти равенства, получим CC

+ BC

= BC, что невозможно. Аналогично рассматриваются осталь-

ные случаи.

Второй способ. Пусть AB + CD = BC + AD. Тогда AB −

− AD = BC − CD. Рассмотрим случай, когда AB > AD

(рис. 174, б ). Тогда BC > CD.

а)

C S B

б )

Рис. 174

210 7 класс

На отрезке AB возьмем такую точку T , чтобы AT = AD,

а на отрезке BC — такую точку S, чтобы CS = CD. Тогда

треугольники T BS, ADT и CDS равнобедренные. Биссектри-

сы их углов при вершинах B, A и C являются серединными

перпендикулярами к отрезкам T S, DT и DS соответственно,

т. е. серединными перпендикулярами к сторонам треугольни-

ка DT S. Поэтому биссектрисы углов B, A и C пересекаются

в одной точке — центре описанной окружности треуголь-

ника DT S. Эта точка равноудалена от всех сторон четы-

рехугольника ABCD. Следовательно, она я вляется центром

вписанной окружности четырехугольника ABCD. Аналогич-

но для AB < AD. Если же AB = AD, то у тверждение оче-

видно.

§ 1.6

1.282. Два луча.

1.283. Серединный перпендикуляр к данному основанию без

середины основания.

1.284. Серединный перпендикуляр к отрезку с концами в

данных точках.

1.285. Окружность с центром в данной точке и радиусом,

равным данному.

1.291. Две прямые, параллельные данной и удаленные от

нее на расстояние, равное данному радиусу.

1.295. Две прямые, параллельные данной.

1.297. Круг, ограниченный данной окружностью, без точек

данной окружности.

1.298. Диаметр данной окружности, перпендикулярный

данной прямой (без концов).

1.299. Окружность, концентрическая данной.

1.303. Биссектриса у гла.

1.304. Указание. Пусть прямые пересекаются. Центр иско-

мой окружности лежит на биссектрисе угла, образованного эти-

ми прямыми, а также на перпендикуляре к прямой, проходящем

через данную на ней точку.

1.305. Четыре точки: одна из них — центр вписанной