Гордин Р.К. Геометрия. Планиметрия. 7-9 классы
Подождите немного. Документ загружается.

§ 1.6 211
Рис. 175
A
O
O
1
Рис. 176
окружности треугольника, остальные — точки пересечения
биссектрис внешних углов.
1.306. Указание. Центры искомых окружностей лежат на
биссектрисах вертикальных углов, образованных данными
прямыми.
1.307. Прямая, проходящая через данную точку и центр
данной окружности (без данной точки).
1.308. Указание. Расстояние между центрами касающихся
окружностей равно сумме или разности их радиусов.
1.309. Одна или две окружности, концентрические дан-
ной.
Поскольку линия центров двух касающихся окруж-
ностей проходит через их точку касания, то искомое геомет-
рическое место точек представляет собой две окружности,
концентрические данной. Радиусы этих окружностей равны
сумме и разности данных радиусов (рис. 175).
1.310. Указание. Пусть данная точка A лежит вне данной
окружности с центром O
1
, а искомая окружность с центром O
касается данной внешним образом (рис. 176). Тогда точка O
лежит на окружности с центром O
1
и радиусом, равным сум-
ме данных радиусов, а также на окружности с центром A и
радиусом, равным данному радиусу искомой окружности.
1.311. Указание. Если искомая окружность касается данной
внешним образом, то ее центр лежит на окружности, концен-
трической данной, с радиусом, равным сумме данных радиусов,
если же внутренним — то разности. В то же время, центр ис-
комой окружности лежит на прямой, параллельной данной и
212 7 класс
A
O
B
Рис. 177
C
M N
A B
Рис. 178
A
O
Рис. 179
удаленной от данной на расстояние, равное данному радиусу
искомой окружности.
1.312. Указание. Диаметр искомой окружности равен рас-
стоянию между данными параллельными прямыми.
1.313. Указание. Диаметр искомой окружности равен рас-
стоянию между данными параллельными прямыми.
1.314. Указание. Центр искомой окружности лежит на
окружностях, соответственно концентрических данным, и ра-
диусы этих окружностей можно найти.
1.315. Указание. Радиус искомой окружности равен полу-
сумме радиусов данных.
1.316. Указание. Пусть A — точка на данной окружности
с центром O (рис. 177), а B — данная точка, не лежащая на
этой окружности. Тогда центр искомой окружности лежит на
серединном перпендикуляре к отрезку AB и на прямой OA.
1.317. Указание. Пусть прямая, проведенная параллельно
стороне AB треугольника ABC (рис. 178) на расстоянии, рав-
ном данной высоте, пересекает стороны AC и BC в точках M
и N. Тогда вершина искомого равнобедренного треугольника
лежит на серединном перпендикуляре к отрезку M N.
1.318. Окружность с диаметром AB (без точки B).
1.319. Указание. Центр искомой окружности лежит на сере-
динном перпендикуляре к отрезку AO (рис. 179), а также — на
окружности с центром O и радиусом, равным половине радиуса
данной окружности.
1.320. Указание. Пусть ABC — искомый треугольник
(рис. 180), AB — его данная сторона, AH — данная высота, O —
§ 1.6 213
O
A B
C
H
Рис. 180
O
A
C
M
Рис. 181
A B
C
O
Рис. 182
центр описанной окружности, R — ее радиус. Тогда точка O —
вершина равнобедренного треугольника с данными сторона-
ми AB и OA = OB = R, а точка H лежит на окружности с
диаметром AB.
1.321. Указание. Если прямые, соответственно параллель-
ные сторонам угла и расположенные на равных расстояниях от
его сторон, пересекаются внутри угла, то точка их пересечения
лежит на биссектрисе данного угла.
1.322. Окружность без одной точки. Указание. Пусть отре-
зок AM делится пополам некоторой точкой K данной окруж-
ности. На продолжении диаметра AB данной окружности за
точку B отложите отрезок BC, равный AB. Треугольник ABM
равнобедренный, так как его медиана BK является высотой.
1.323. Указание. Биссектриса есть ось симметрии угла.
1.324. Окружность с центром O и радиусом OA (без точ-
ки A) и луч OC (без точки O).
Если точка M из искомого гео-
метрического места точек не лежит на прямой AO (рис. 181), то
из теоремы о внешнем угле треугольника следует, что треуголь-
ник AOM — равнобедренный (MO = OA). Поэтому точка M
лежит на окружности с центром O и радиусом OA. Обратно,
для любой точки M окружности с центром O и радиусом OA,
отличной от A, ∠MOC = 2∠MAC. Если точка M, отличная
от O, лежит на луче OC, то
∠MOC = 2∠MAC.
1.325. Указание. Если O — точка пересечения биссектрис
треугольника ABC (рис. 182) и ∠AOB = 135
◦
, то ∠ACB = 90
◦
.
214 7 класс
Рис. 183
AB
C
D
X
X
1
X
2
M
O
Рис. 184
1.326. а) Внешность круга, построенного на данном отрезке
как на диаметре, без точек прямой, проходящей через данные
точки; б) внутренность круга, построенного на данном отрез-
ке как на диаметре, без точек прямой, проходящей через дан-
ные точки. Указание. Примените теорему о внешнем угле тре-
угольника.
1.327. Указание. Равные хорды окружности касаются неко-
торой окружности, концентрической данной.
1.328. Геометрическое место середин равных хорд окруж-
ности есть окружность, концентрическая данной. Радиус этой
окружности равен расстоянию от центра данной окружности
до одной из таких хорд. Отсюда вытекает следующее построе-
ние. Впишем в первую окружность произвольную хорду, равную
данному отрезку (рис. 183). Построим окружность, концентри-
ческую данной, с радиусом, равным расстоянию от центра до
середины построенной хорды. Аналогично для второй окруж-
ности. Тогда каждая общая касательная к двум построенным
окружностям есть искомая прямая. Задача может иметь не бо-
лее четырех решений.
1.329. Указание. Через данную на одной из окружностей
точку проведите касательную к этой окружности. Теперь за-
дача сводится к построению окружности, касающейся данной
окружности и данной прямой в данной на ней точке (пример 4
из §1.5, с. 35).
1.330. Две равные касающиеся окружности.
Пусть CD —
диаметр данной окружности, перпендикулярный данному

§ 1.7 215
диаметру AB (рис. 184), X — произвольная точка меньшей
дуги AC, X
1
и X
2
— проекции точки X на AB и OC соот-
ветственно. Тогда OC = OX, OM = XX
1
= OX
2
. Поэтому
треугольники CMO и XX
2
O равны по двум сторонам и углу
между ними. Значит, ∠CMO = ∠XX
2
O = 90
◦
. Следовательно,
точка M лежит на окружности с диаметром OC. Аналогично
для любой другой точки данной окружности.
Пусть теперь M — произвольная точка окружности с диа-
метром OC. Пусть X — точка пересечения луча OM с исходной
окружностью, X
1
и X
2
— проекции точки X на AB и OC соот-
ветственно. Тогда прямоугольные треугольники CMO и XX
2
O
равны по гипотенузе и острому углу. Следовательно, OM =
= OX
2
= XX
1
. Аналогично для любой точки окружности с
диаметром OD.
1.331. Указание. См. пример 3 из §1.6, с. 43.
§ 1.7
1.333. Сторона, равная 1. 1.334. Нет. 1.335. Может. 1.336.
Нет. 1.340. а) 3; б) 13. 1.341. 6. 1.342. 60
◦
. 1.343. BC.
1.344. Указание. Если хорда AB не является диаметром
окружности с центром O (рис. 185), то для равнобедренного
треугольника AOB верно неравенство AB < OA + OB.
1.346. а) Да; б) нет.
1.347. Указание. Если CD — высота прямоугольного тре-
угольника ABC, проведенная к гипотенузе AB (рис. 186), то
∠ACD = ∠ABC и ∠BCD = ∠BAC.
1.348. AB > AC. Указание. Если ∠BAD > ∠CAD
(рис. 187), то
∠ABC = 90
◦
− ∠BAD < 90
◦
− ∠CAD = ∠ACB.
A
B
O
Рис. 185
C
A D B
Рис. 186
A
B D C
Рис. 187

216 7 класс
A
B
C
D
Рис. 188
A
B
C
D
M
Рис. 189
A
B CM
Рис. 190
A
B C
M
K
Рис. 191
1.349. Пусть a, b, c — стороны треугольника. Тогда a + b +
+ c = a + (b + c) > a + a = 2a, поэтому a <
1
2
(a + b + c).
1.350. Пусть AC — диагональ четырехугольника ABCD
(рис. 188). Применяя неравенство треугольника к треугольни-
кам ABC и ACD, получим AC < AB + BC и AC < AD + CD.
Сложив почленно эти неравенства, найдем
2AC < AB + BC + AC + CD,
откуда AC <
1
2
(AB + BC + AC + CD).
1.351
0
. Пусть M — точка пересечения диагоналей AC и BD
данного четырехугольника ABCD (рис. 189). Тогда AB < AM +
+ BM и CD < CM + DM. Сложив почленно эти неравенства,
получим
AB + CD < AM + BM + CM + DM =
= (AM + CM) + (BM + DM ) = AC + BD.
1.352. В точке пересечения диагоналей четырехугольника.
Указание. Предположите, что искомая точка не лежит на одной
из диагоналей, и примените неравенство треугольника.
1.353. Указание. Воспользуйтесь результатами задач 1.350
и 1.351
0
.
1.354. Пусть M — точка на основании BC равнобедренного
треугольника ABC, отличная от точек B и C (рис. 190). Тогда
один из углов AM B и AMC прямой или тупой. Предположим,
∠AMB > 90
◦
. Тогда это наибольший угол треугольника AMB,
значит, AM < AB.
§ 1.7 217
O
1
O
2
A
Рис. 192
O
1
O
2
A B
M N
X
Y
Рис. 193
1.355. Через точку K проведем пря мую, параллельную ос-
нованию BC (рис. 191). Пусть M — ее точка пересечения с бо-
ковой стороной AB. Тогда ∠BKM = ∠CBK = ∠ABK, значит,
треугольник BMK равнобедренный, BM = MK = KC. Следо-
вательно, 2CK = BM + M K > BK.
1.356
0
. Пусть O
1
и O
2
— центры окружностей радиусов r
и R соответственно (рис. 192), A — одна из двух точек их пере-
сечения. Для треугольника O
1
AO
2
верны неравенства
O
1
O
2
< O
1
A + O
2
A и AO
2
< O
1
A + O
1
O
2
,
или
O
1
O
2
< r + R и O
1
O
2
> AO
2
−AO
1
= R −r.
1.357
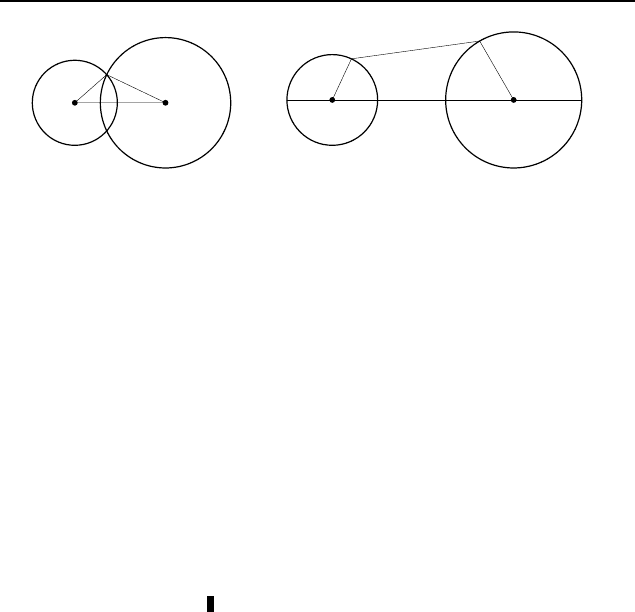
0
. 3 и 13.
Докажем, что кратчайшее расстояние
между точками двух окружностей, лежащих одна вне другой,
есть отрезок линии центров, заключенный между окружностя-
ми. Пусть O
1
и O
2
— центры окружностей, а линия центров
пересекает окружности в точках A и B, причем и A, и B лежат
между O
1
и O
2
(рис. 193). Тогда, если X и Y — другие точки
этих окружностей, то
XO
1
+ XY + Y O
2
> O
1
O
2
= AO
1
+ AB + BO
2
.
Следовательно, XY > AB. Пусть AM и BN — диаметры
окружностей, а X и Y — точки окружностей, отличные от M
и N. Тогда
XY < XO
1
+ O
1
O
2
+ Y O
2
= M O
1
+ O
1
O
2
+ NO
2
= M N.
В нашей задаче AB = 3 и MN = 2 + 8 + 3 = 13.

218 7 класс
A
B C
M
D
A
1
B
1
C
1
M
1
D
1
Рис. 194
A
B C
K
M
Рис. 195
1.358. Указание. Если O — точка пересечения биссектрис
треугольника ABC, то ∠BOC = 90
◦
+
1
2
∠A.
1.359. Нет.
1.360. Пусть ABC и A
1
B
1
C
1
— равнобедренные треуголь-
ники с основаниями BC и B
1
C
1
(рис. 194), причем AB = AC =
= A
1
B
1
= A
1
C
1
и ∠A > ∠A
1
, а AD и A
1
D
1
— их высоты.
На продолжениях AD и A
1
D
1
за точки D и D
1
отложим от-
резки DM и D
1
M
1
, соответственно равные AD и A
1
D
1
. Тогда
в треугольниках ACM и A
1
C
1
M
1
известно, что AC = A
1
C
1
,
CM = C
1
M
1
и ∠ACM < ∠A
1
C
1
M
1
. Значит, AM < A
1
M
1
. Сле-
довательно, AD < A
1
D
1
.
1.361. Указание. Воспользуйтесь результатом задачи 1.360.
1.362. Указание. Воспользуйтесь результатом задачи 1.360.
1.363. Указание. Искомая хорда перпендикулярна радиусу,
проходящему через данную точку (для доказательства восполь-
зуйтесь утверждением задачи 1.362).
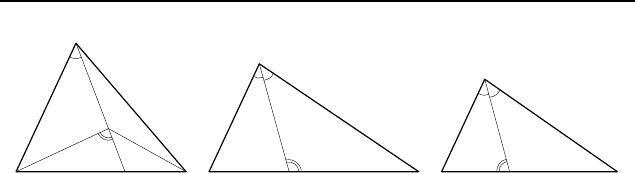
1.364
0
. Отложим на продолжении медианы AM за точ-
ку M отрезок MK, равный AM (рис. 195). Тогда CK = AB.
Применяя неравенство треугольника к треугольнику ABK,
получим
2AM = AK < AB + BK = AB + AC
и
2AM = AK > AB − BK = AB −AC.
Отсюда следует, что
1
2
(AB − AC) < AM <
1
2
(AB + AC).
§ 1.7 219
A
B CK
M
Рис. 196
C
B AK
Рис. 197
B
A D C
Рис. 198
1.365. Продолжим AM до пересечения со стороной BC в
точке K (рис. 196). Тогда
∠BMK = ∠BAM + ∠ABM > ∠BAM
и
∠CMK = ∠CAM + ∠ACM > ∠CAM.
Следовательно,
∠BMC = ∠BMK + ∠CM K > ∠BAM + ∠CAM = ∠BAC.
1.366. Поскольку угол B треугольника BCK (рис. 197)
больше угла A треугольника ACK (против большей сторо-
ны AC треугольника ABC лежит больший угол), а углы BCK
и ACK этих треугольников равны, то ∠BKC < ∠AKC, а так
как это смежные углы, то угол AKC тупой.
1.367. Угол ADB — внешний угол треугольника BDC
(рис. 198), поэтому ∠ADB > ∠CBD = ∠ABD, значит, в тре-
угольнике ABD сторона AB больше стороны AD. Аналогично,
CB > CD.
1.368. Отложим на продолжении медианы CD за точ-
ку D отрезок DC
1
, равный DC (рис. 199). Тогда AC
1
= BC
и ∠AC
1
C = ∠BCD. В треугольнике CAC
1
известно, что AC >
> AC
1
= BC. Следовательно,
∠ACD = ∠ACC
1
< ∠AC
1
C = ∠BCD.
1.369. Пусть BD — биссектриса треугольника ABC
(рис. 200) и AB > BC. Рассмотрим точку C
1
, симметричную

220 7 класс
C
B A
C
1
D
Рис. 199
B
ADC
C
1
Рис. 200
B
A C
M
N
Рис. 201
вершине C относительно биссектрисы угла B. Тогда CD = C
1
D.
Поскольку BC
1
= BC < AB, точка C
1
лежит на отрез-
ке AB, а AC
1
D — внешний угол треугольника BDC
1
, по-
этому ∠AC
1
D > ∠BDC
1
= ∠BDC > ∠A. Следовательно,
CD = C
1
D < AD.
1.370. Указание. Предположите противное и воспользуй-
тесь результатом предыдущей задачи.
1.371. В треугольнике ABN (рис. 201) угол B наибольший,
поэтому AN > AB, а так как AM — биссектриса треуголь-
ника ABN, то M N > BM (см. задачу 1.121
0
). Неравенство
MN < NC доказывается аналогично.
1.372. Указание. Воспользуйтесь результатом задачи 1.368.
1.373. Содержащая точку B полуплоскость, граница кото-
рой — серединный перпендикуляр к отрезку AB.
1.374. Поскольку ∠AM N = ∠MCN + ∠MNC > ∠C, то
угол AMN тупой (рис. 202). Следовательно, AN — наибольшая
сторона треугольника AMN. Тогда MN < AN . Аналогично
докажем, что AB — наибольшая сторона треугольника ANB.
Поэтому AN < AB. Следовательно, MN < AB.
1.375. Пусть D — точка на стороне BC треугольника ABC
(рис. 203). Один из углов ADB и ADC не меньше прямого.
Пусть ∠ADC > 90
◦
. Тогда это наибольший угол треугольни-
C
A B
M
N
Рис. 202
A
B D C
Рис. 203
