Гордин Р.К. Геометрия. Планиметрия. 7-9 классы
Подождите немного. Документ загружается.

§ 2.4 261
A
P
C
E
M
F
O
2
O
O
1
BK
Рис. 306
P R
O
1
O
2
Q
N
M
Рис. 307
и
O
1
M
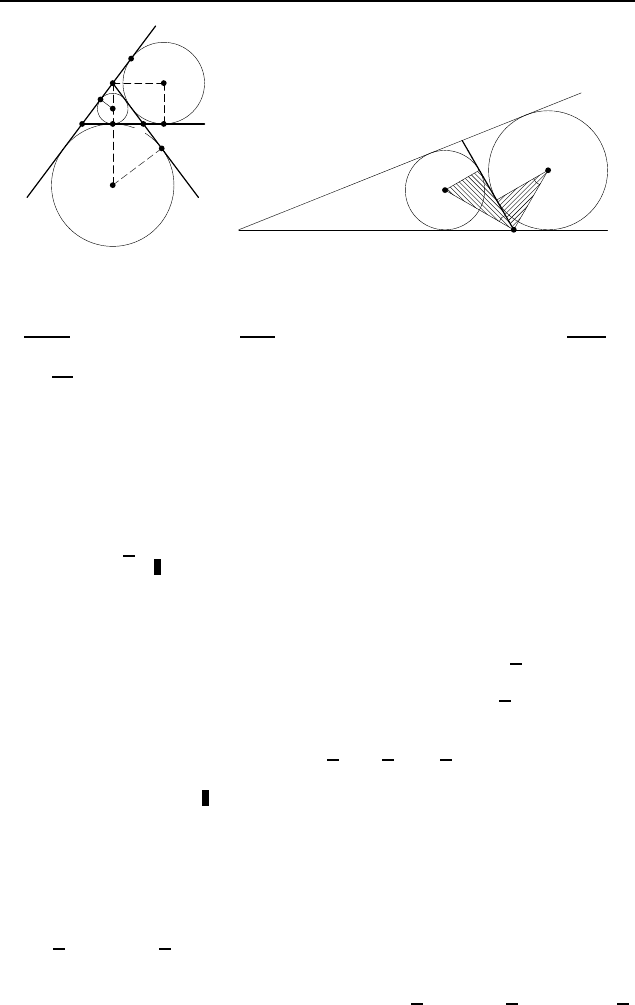
MC
= tg ∠BCK =
BK
KC
, откуда r
1
= O
1
M = BK ·
MC
KC
=
= 6 ·
16
8
= 12.
Пусть окружность с центром O
2
касается продолжения сто-
роны AB в точке F , а продолжения стороны AC — в точ-
ке E. Поскольку CO
2
— биссектриса угла BCE, а CK — бис-
сектриса его смежного угла ACB, то ∠O
2
CK = 90
◦
. Поэто-
му O
2
CKF — прямоугольник. Следовательно, r
3
= r
2
= O
2
F =
= CK = 8.
2.238.
√
3. Пусть O
1
и O
2
— центры окружностей ра-
диусов 2 и 3 соответственно, M и N — их точки касания со
стороной RQ (рис. 307). Тогда
RM = O
1
M ctg ∠MRO
1
= 2 ctg 30
◦
= 2
√
3,
RN = O
2
N ctg ∠NRO
2
= 3 ctg 60
◦
=
√
3.
Поэтому M N = RM − RN = 2
√
3 −
√
3 =
√
3.
2.239. 30
◦
, 90
◦
.
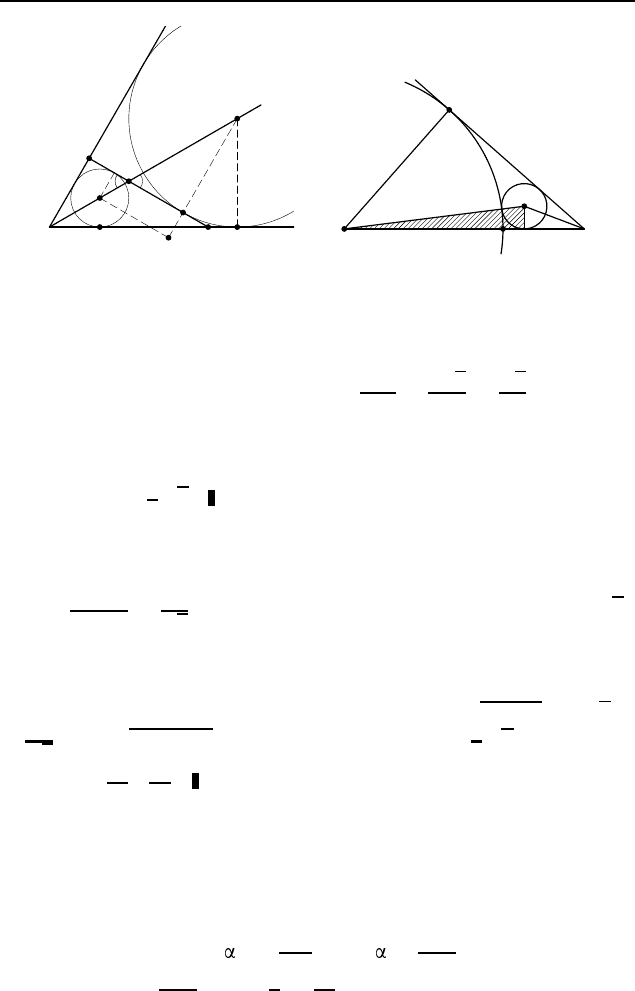
Пусть окружность с центром O, вписан-
ная в треугольник ABC (рис. 308), касается сторон AB и BC в
точках M и P соответственно, а вторая окружность с центром Q
касается стороны BC в точке F , а продолжения стороны AB —
в точке N. Поскольку центры этих окружностей расположены
на биссектрисе угла BAC, то OQ = AQ −AO = 2QN −2OM =
= 2
√
3 + 2 − 2
√
3 + 2 = 4. Пусть D — точка пересечения отрез-
ка OQ со стороной BC, а K — проекция точки O на прямую QF .
Тогда QK = QF + F K = QF + OP =
√
3 + 1 +
√
3 − 1 = 2
√
3.
262 8 класс
A M
K
B N
Q
C
D
F
O
P
Рис. 308
P AO
M
Q
K
Рис. 309
Поэтому
sin ∠P DO = sin ∠QOK =
QK
OQ
=
2
√
3
4
=
√
3
2
,
значит, ∠CDA = ∠P DO = 60
◦
. Следовательно, ∠ABC =
= ∠CDA − ∠BAD = 30
◦
, а ∠ACB = 90
◦
.
2.240. 2 −
4
3
√
2. Пусть Q — центр искомой окружности,
x — ее радиус, P — точка касания искомой окружности с отрез-
ком AM (рис. 309). Тогда
OA =
OK
sin 60
◦
=
4
√
3
, AP = QP ctg ∠P AQ = x ctg 30
◦
= x
√
3,
OQ = 2 + x, OP
2
= OQ
2
− QP
2
= (2 + x)
2
−x
2
= 4 + 4x.
Поскольку OP + AP = OA, имеем уравнение
√
4 + 4x + x
√
3 =
=
4
√
3
, или
√
12 + 12x = 4 − 3x, откуда x = 2 −
4
3
√
2.
2.241.
15
4
,
20
3
.
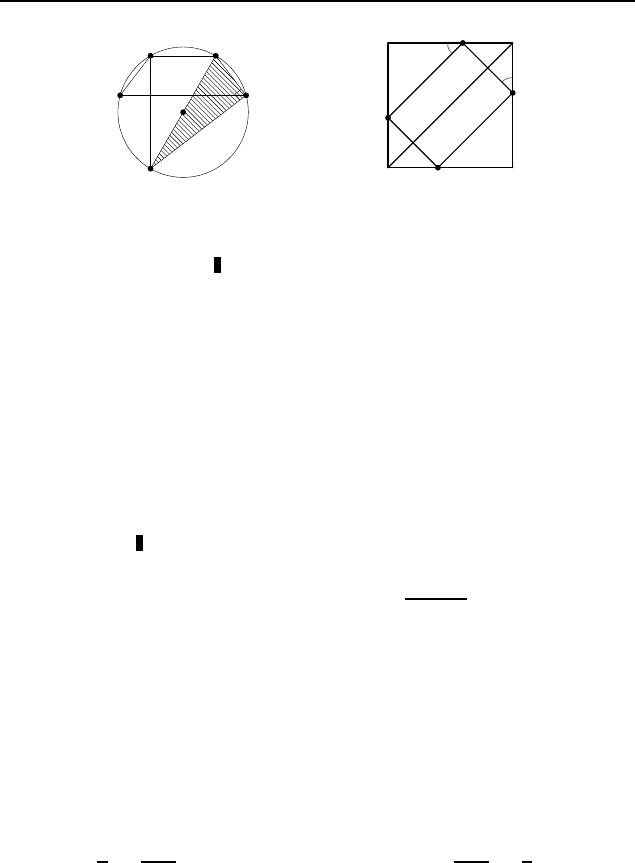
Пусть A и B — указанные точки каса-
ния (AC = 6, BC = 8). Поскольку треугольник ABC прямо-
угольный (угол C — прямой), то AB = 10. Пусть M — ос-
нование перпендикуляра, опущенного из центра O окружно-
сти на хорду BC этой окружности. Углы MBO и CAB рав-
ны, так как каждый из них в сумме с углом ABC составля-
ет 90
◦
. Если ∠BAC = , то
AC
AB
= cos
=
BM
OB
, откуда находим,
что BO = AB ·
BM
AC
= 10 ·
4
6
=
20
3
. Аналогично находим радиус
второй окружности.
§ 2.4 263
A
C
D
1
B
D
P
Рис. 310
A B
CD
K
L
M
N
a b
c
d
a
b
c
d
Рис. 311
2.242. 8R
2
, 4R
2
.
Проведем диаметр DD
1
(рис. 310). То-
гда BD
1
k AC. Следовательно, AB = D
1
C. По теореме Пифаго-
ра из прямоугольного треугольника DCD
1
находим, что AB
2
+
+CD
2
= D
1
C
2
+DC
2
= DD
2
1
= 4R
2
. Аналогично, BC
2
+AD
2
=
= 4R
2
. Следовательно,
AB
2
+ BC
2
+ CD
2
+ AD
2
= 8R
2
,
AP
2
+ BP
2
+ CP
2
+ DP
2
= (AP
2
+ BP
2
) + (CP
2
+ DP
2
) =
= AB
2
+ CD
2
= 4R
2
.
2.243. 1.
Стороны треугольника с вершинами в центрах
данных окружностей равны 3, 4, 5. Значит, он прямоугольный.
Радиус его вписанной окружности равен
3+4−5
2
= 1. Эта окруж-
ность проходит через точки касания трех данных окружностей.
Других таких окружностей нет.
2.244. Пусть вершины K, L, M и N прямоугольника KLMN
расположены соответственно на сторонах AB, BC, CD и AD
квадрата ABCD (рис. 311). Обозначим AK = a, BK = b,
BL = c и CL = d. Тогда CM = a, DM = b, DN = c и AN = d,
причем a 6= c, так как в противном случае KLMN — квадрат.
Тогда
d
a
=
AN
AK
= tg ∠AKN = tg ∠BLK =
BK
BL
=
b
c
,
значит, ab = cd. Кроме того, a + b = c + d. Из полученных
равенств следует, что либо a−b = c−d, что невозможно, либо a−
−b = d−c. В последнем случае a = d и b = c. Тогда ∠AKN = 45
◦
и ∠BKL = 45
◦
. Следовательно, KN k BD и KL k AC.
2.245. Прямая, перпендикулярная AB.

264 8 класс
O
1
O
2
M
t
t
R
r
Рис. 312
AB
C
D
P
Рис. 313
A
B C
H
Рис. 314
2.246. Прямая, перпендикулярная линии центров, или часть
такой пря мой.
Пусть R и r — радиусы данных окружно-
стей с центрами O
1
и O
2
соответственно (рис. 312), M — точка,
для которой выполнено данное условие. Если t — длина каса-
тельных, то O
1
M
2
= t
2
+ R
2
, O
2
M
2
= t
2
+ r
2
. Это означает,
что точка M лежит на перпендикуляре к O
1
O
2
, для которо-
го O
1
M
2
− O
2
M
2
= R
2
− r
2
. При этом в наше геометрическое
место входят все точки этого перпендикуляра, если окружности
расположены одна вне другой. Для пересекающихся окружно-
стей исключается их общая хорда.
2.247. Необходимость. Пусть прямые AB и CD перпенди-
кулярны (рис. 313). Если P их точка пересечения, то по теореме
Пифагора AC
2
− BC
2
= AP
2
− BP
2
= AD
2
− BD
2
, отку-
да AC
2
+ BD
2
= AD
2
+ BC
2
.
Достаточность. Пусть AC
2
+ BD
2
= AD
2
+ BC
2
. Рассмот-
рим отрезок AB. Известно, что геометрическое место точек X,
для которых разность AX
2
−BX
2
постоянна, есть перпендику-
ляр к отрезку AB. Поскольку точки C и D удовлетворяют этому
условию, они лежат на этом перпендикуляре. Следовательно,
AB ⊥ CD.
2.248. Пусть высоты треугольника ABC, проведенные из
вершин B и C, пересекаются в точке H (рис. 314). Тогда по
предыдущей задаче AC
2
+ BH
2
= BC
2
+ AH
2
и AB
2
+ CH
2
=
= BC
2
+ AH
2
, поэтому AC
2
+ BH
2
= AB
2
+ CH
2
. Следователь-
но, AH ⊥ BC, т. е. высота, проведенная из вершины A, проходит
через точку H.
2.249.
8
5
R
2
.
Обозначим AB = x, BC = 2x, CD = y,
AD = z (рис. 315). Поскольку диагонали четырехугольника

§ 2.5 265
A
B
C
D
Рис. 315
CAM
F
E
N
B
P
Q
Рис. 316
A
B C
B
1
C
1
C
2
B
2
Рис. 317
взаимно перпендикулярны, суммы квадратов его противопо-
ложных сторон равны между собой, т. е. x
2
+ y
2
= z
2
+ 4x
2
,
а так как в четырехугольник можно вписать окружность,
то x + y = z + 2x. Возведя обе части этого равенства в квад-
рат и вычитая результат почленно из предыдущего, найдем,
что y = 2z. Из равенства x + y = z + 2x следует, что z = x
и y = 2x. Поскольку точки A и C равноудалены от кон-
цов хорды BD, хорда AC — диаметр окружности. Поэто-
му ∠ABC = 90
◦
. Из уравнения x
2
+ 4x
2
= 4R
2
находим,
что x
2
=
4
5
R
2
. Следовательно, S
ABCD
= 2S
ABC
= 2x
2
=
8
5
R
2
.
2.250.
r
a
2
2
+ ab + b
2
.
Пусть P и Q — центры квадра-
тов BEF C и ABNM соответственно (рис. 316). Тогда AQ =
b
√
2
,
а из задачи 2.232 следует, что AP =
a+b
√
2
. Из прямоугольного
треугольника QAP находим
P Q
2
= AQ
2
+ AP
2
=
b
2
2
+
b
2
2
+ ab +
a
2
2
=
a
2
2
+ ab + b
2
.
2.251. В прямоугольных треугольниках AB
2
C и AC
2
B
(рис. 317) отрезки B
2
B
1
и C
2
C
1
— высоты, проведенные из вер-
шин прямых углов, поэтому AB
2
= AC ·AB
1
и AC
2
= AB ·AC
1
.
С другой стороны,
AB
1
AB
= cos ∠A =
AC
1
AC
, откуда AB
1
· AC =
= AC
1
· AB. Следовательно, AB
2
2
= AC
2
2
и AB
2
= AC
2
.
§ 2.5
2.252.
√
2. 2.253. AB = AC =
√
130.
2.254. Стороны треугольника равны
√
80,
√
205,
√
125.
266 8 класс
2.255. Указание. AB + BC = AC.
2.256. (8; 3). 2.257. а) (−1; −3); б) (1; 3); в) (1; −3); г) (7; −1);
д) (3; −1); е) (−3; 1).
2.258. Указание. Диагонали четырехугольника ABCD рав-
ны и делятся точкой пересечения пополам.
2.259. B. 2.260. а) y − 1 = 0; б) x + 3 = 0. 2.261.
√
410
4
.
2.262. 2x − 3y + 12 = 0. 2.263. x − 1 = 0.
2.264.
2
3
;
14
3
, (−5; −1),
7
2
; −1
.
2.265. AB: x + 2 = 0; AC: x − 2y + 6 = 0; BC: x −y = 0.
2.266. x − 2y − 2 = 0. 2.267. (x − 3)
2
+ (y − 1)
2
= 10.
2.268. а) (3; −2), R = 4; б) (1; −3), R = 5; в)
1
2
;
1
2
, R = 1.
2.269. (x − 2)
2
+ (y − 3)
2
= 13. 2.270. 3
√
10. 2.271. (−3; 4).
2.272. (x − 5)
2
+ (y − 5)
2
= 25 или (x − 1)
2
+ (y − 1)
2
= 1.
Указание. Уравнение искомой окружности имеет вид (x −a)
2
+
+ (y − a)
2
= a
2
.
2.273. (3; 3), (−3; 5).
2.274. Точка B лежит на окружности, точки A и D — внут-
ри, точка C — вне окружности.
2.275. (−2; 3). Указание. Примените теорему о пропорцио-
нальных отрезках.
2.276. (3; 1). 2.277. (4; 1). 2.281.
x −
7
2
2
+
y − 2
2
=
125
4
.
2.282. 3x + 4y − 28 = 0 или y − 7 = 0. Указание. Уравнение
искомой касательной имеет вид y = kx + 7. Подставив в уравне-
ние окружности kx+7 вместо y, получим квадратное уравнение
относительно x. Его дискриминант должен быть равен 0.
2.283
0
. Указание. Если одна из двух перпендикулярных
прямых образует с осью абсцисс острый угол
, то вторая —
тупой угол 90
◦
+
.
2.284. Указание. Составьте уравнения прямых AC и BD и
убедитесь, что произведение их угловых коэффициентов рав-
но −1.
2.285. 2x + y − 2 = 0. 2.286. x + 3y − 9 = 0. 2.287. (3; −5).
2.288. Пусть стороны данного прямоугольника равны a и b.
Поместим начало координат в одну из вершин прямоугольни-
ка, а оси координат направим по двум его соседним сторонам
(рис. 318). Тогда точки A(0; 0), B(0; b), C(a; b) и D(a; 0) —

§ 2.5 267
A(0; 0)
B(0; b) C(a; b)
D(a; 0)
M(x; y)
x
y
Рис. 318
A(0; 0) B(a; 0)
M(x; y)
x
y
Рис. 319
вершины прямоугольника. Если M(x; y) — произвольная точка
плоскости, то
MA
2
+ MC
2
= (x
2
+ y
2
) + ((x − a)
2
+ (y − b)
2
),
MB
2
+ MD
2
= (x
2
+ (y − b)
2
) + ((x − a)
2
+ y
2
),
следовательно,
MA
2
+ MC
2
= MB
2
+ MD
2
.
2.289. Прямая, перпендикулярная отрезку с концами в дан-
ных точках.
Пусть расстояние между данными точками A
и B равно a. Поместим начало координат в точку A, ось абс-
цисс направим вдоль луча AB, а ось ординат — вдоль лу ча AY ,
перпендикулярного AB (рис. 319). Тогда точка A имеет коор-
динаты (0; 0), а точка B — (a; 0). Пусть M(x; y) — произволь-
ная точка плоскости, для которой AM
2
− BM
2
= c > 0. То-
гда (x
2
+ y
2
) −((x −a)
2
+ y
2
) = c, или x =
a
2
+c
2a
, а это уравнение
прямой, перпендикулярной оси абсцисс.
2.290. Окружность (при k 6= 1) или прямая (при k = 1).
Пусть расстояние между данными точками A и B равно a.
Поместим начало координат в точку A, ось абсцисс направим
вдоль луча AB, а ось ординат — вдоль луча AY , перпендику-
лярного AB (рис. 319). Тогда точка A имеет координаты (0; 0),
а точка B — (a; 0). Пусть M (x; y) — произвольная точка плос-
кости. Если k = 1, получим геометрическое место точек, рав-
ноудаленных от A и B, т. е. прямую x =
1
2
a. Пусть k 6= 1.
Условие AM = kBM равносильно условию AM
2
= k
2
· BM
2
,
или x
2
+ y
2
= k
2
(x − a)
2
+ k
2
y
2
. После раскрытия скобок,

268 8 класс
приведения подобных и выделения полного квадрата получим
уравнение
x −
ak
2
k
2
− 1
2
+ y
2
=
a
2
k
2
(k
2
− 1)
2
.
Это уравнение окружности с центром в точке
ak
2
k
2
−1
; 0
и ра-
диусом
ak
|k
2
−1|
(окружность Аполлония).
2.291. При d >
1
2
a
2
— окружность, при d =
1
2
a
2
— точка,
при d <
1
2
a
2
— пустое множество (a — расстояние между данны-
ми точками A и B).
Поместим начало координат в точку A,
ось абсцисс направим вдоль луча AB, а ось ординат — вдоль лу-
ча AY , перпендикулярного AB (рис. 319). Тогда точка A имеет
координаты (0; 0), а точка B — (a; 0). Пусть M(x; y) — произ-
вольная точка плоскости. Условие AM
2
+BM
2
= d равносильно
условию x
2
+y
2
+(x−a)
2
+y
2
= d. После раскрытия скобок, при-
ведения подобных и выделения полного квадрата получим урав-
нение
x−
1
2
a
2
+y
2
=
1
4
(2d−a
2
). Если d >
1
2
a
2
— это уравнение
окружности с центром в точке
1
2
a; 0
и радиусом
1
2
√
2d − a
2
,
при d =
1
2
a
2
получим точку
1
2
a; 0
. В остальных случаях полу-
чим пустое множество.
2.292. Пусть b 6= 0. Тогда уравнение данной прямой можно
представить в виде y = −
a
b
x−
c
b
. Уравнение прямой, проходящей
через точку M перпендикулярно данной прямой, имеет вид y −
− y
0
=
b
a
(x − x
0
). Запишем уравнение данной прямой в виде
a(x − x
0
) + b(y − y
0
) + ax
0
+ by
0
+ c = 0. Решив систему двух
последних уравнений относительно x − x
0
и y − y
0
, получим
x − x
0
= −
a
a
2
+ b
2
(ax
0
+ by
0
+ c),
y − y
0
= −
b
a
2
+ b
2
(ax
0
+ by
0
+ c),
где x и y — координаты точки H пересечения прямых. Тогда
квадрат искомого расстояния равен
MH
2
= (x − x
0
)
2
+ (y − y
0
)
2
=
(ax
0
+ by
0
+ c)
2
a
2
+ b
2
.
§ 2.5 269
P (1; 3)
M(a; b)
N(−1; 1)
O
K
x
y
Рис. 320
O
2
(a; 0)
O
1
(−b; 0)
B
C
M
A
x
y
Рис. 321
2.293.
9
√
10
. 2.294. (x − 3)
2
+ (y − 2)
2
= 20. 2.295. 5.
2.296. x = (1 −
)x
1
+ x
2
, y = (1 − )y
1
+ y
2
.
2.297. Пусть прямые AB и ax + by + c = 0 пересекаются в
точке C. Обозначим AC : AB =
. Докажем, что 0 < < 1. Это
будет означать, что точка C расположена между точками A и B,
т. е. точки A и B лежат по разные стороны от данной прямой.
Точка C имеет координаты x = (1−
)x
1
+ x
2
, y = (1− )y
1
+ y
2
(см. задачу 2.296). Подставляя их в уравнение данной прямой,
находим, что
= 1
1 −
ax
2
+by
2
+c
ax
1
+by
1
+c
, а так как
ax
2
+by
2
+c
ax
1
+by
1
+c
< 0,
то 0 <
< 1. Что и требовалось доказать.
2.298. 2
√
2. Рассмотрим на координатной плоскости xOy
(рис. 320) точку M(a; b). Пусть d — расстояние от этой точ-
ки до прямой x + y = 0, а c — до точки P (1; 3). Тогда d =
=
|a+b|
√
2
, c =
p
(a − 1)
2
+ (b − 3)
2
. Если K — точка пересечения
прямых x + y = 0 и x = a, то MK = d
√
2 = |a + b|. Точ-
ка N(−1; 1) — проекция точки P на прямую x+y = 0. Тогда |a+
+ b| +
p
(a − 1)
2
+ (b − 3)
2
= MK + MP > KP > P N = 2
√
2,
причем равенство достигается, когда точка M совпадает с точ-
кой N.
2.299. Окружность.
Пусть a и b — радиусы окружно-
стей. Поместим начало координат в точку A, ось абсцисс напра-
вим по линии центров окружностей (рис. 321), ось ординат —
по лучу AY , перпендикулярному линии центров. Пусть (a; 0)
и (−b; 0) — координаты центров окружностей и a > b. Тогда
уравнения окружностей имеют вид (x − a)
2
+ y
2
= a
2
и (x +
+ b)
2
+ y
2
= b
2
. Уравнение прямой, отличной от оси ординат и
270 8 класс
x
1
x
2
x
3
x
4
O
x
y
Рис. 322
A(x
1
; y
1
)
B(r; 0)
0
C
x
y
Рис. 323
проходящей через точку A, имеет вид y = kx. Подставив kx
вместо y в уравнение каждой из окружностей, найдем коор-
динаты отличных от A точек B и C пересечения этой прямой
с окружностями: B
2a
k
2
+1
;
2ka
k
2
+1
, C
−
2b
k
2
+1
; −
2kb
k
2
+1
. Если x —
абсцисса точки M, середины отрезка BC, то x =
a−b
k
2
+1
> 0.
Отсюда находим, что k
2
=
a−b−x
x
. Если k > 0, то y
2
= k
2
x
2
,
или y
2
= x(a − b − x). После раскрытия скобок, приведения
подобных и выделения полного квадрата получим уравнение
x −
a−b
2
2
+ y
2
=
(a−b)
2
4
. Это уравнение верхней полуокруж-
ности с центром в точке
a−b
2
; 0
и радиусом
a−b
2
. Для k < 0
получим уравнение нижней полуокружности с теми же центром
и радиусом.
2.300. Пусть некоторая прямая пересекает параболу y = x
2
в точках с абсциссами x
1
и x
2
, а параллельная ей прямая —
в точках с абсциссами x
3
и x
4
(рис. 322). Тогда
x
2
2
− x
2
1
x
2
− x
1
=
x
2
4
− x
2
3
x
4
− x
3
= k,
где k — угловой коэффициент прямых. Отсюда следует, что
x
1
+ x
2
= x
3
+ x
4
, или
x
1
+x
2
2
=
x
3
+x
4
2
, т. е. абсциссы середин от-
резков параллельных прямых, высекаемых данной параболой,
совпадают. Следовательно, прямая, проходящая через середи-
ны таких отрезков, параллельна оси ординат. Отсюда вытекает
нужное построение.
2.301. Пусть точка A(x
1
; y
1
) лежит на данной окружности
и числа x
1
и y
1
рациональны (рис. 323). На отрезке [−
√
R;
√
R]
