Гордин Р.К. Геометрия. Планиметрия. 7-9 классы

Подождите немного. Документ загружается.

§ 2.6 281

A B

Рис. 342

B C

Рис. 343

A B

Рис. 344

хорду A

на угол KOK

вокруг точки O так, чтобы точка K

совпала с K.

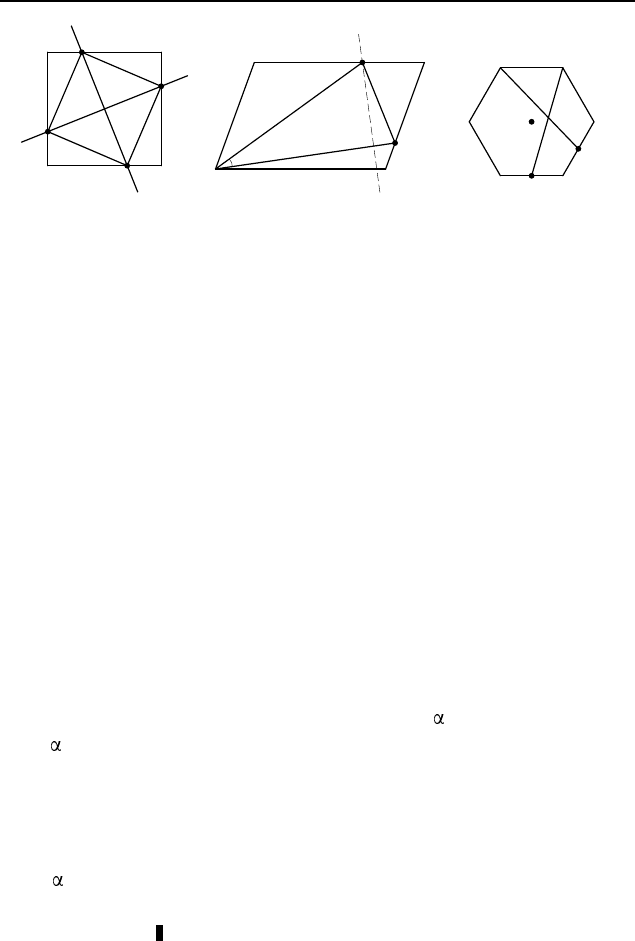
2.356. Пусть данные перпендикулярные прямые, проходя-

щие через центр O квадрата ABCD (рис. 342), пересекают сто-

роны AB, BC, CD и DA соответственно в точках M , N , K

и L (в обоих случаях точки перечислены по часовой стрелке).

При повороте вокруг точки O на угол 90

◦

по часовой стрел-

ке прямая AB переходит в прямую BC, а прямая M K — в

прямую N L. Следовательно, точка M пересечения прямых AB

и KM переходит в точку N пересечения прямых BC и LN.

Аналогично для остальных вершин четырехугольника MN KL.

Таким образом, при повороте относительно точки O на 90

◦

че-

тырехугольника MNKL переходит в себя. Следовательно, это

квадрат.

2.358. а) M

(−y; x); б) M

(y; −x).

2.359. Предположим, что нужные точки M и N построены

(рис. 343). Пусть AM = AN, ∠MAN =

. При повороте на

угол

относительно точки A, переводящем точку N в точку M,

прямая CD переходит в прямую, пересекающую отрезок BC в

точке M .

Отсюда вытекает следующий способ построения. Строим об-

раз прямой CD при повороте относительно точки A на данный

угол

. Точка пересечения построенной прямой с отрезком BC

(если она существует) есть искомая точка M .

2.360. 60

◦

. При повороте на 60

◦

относительно центра O

правильного шестиугольника ABCDEF (рис. 344), переводя-

щем вершину A в вершину B, вершина C переходит в верши-

ну D, а вершина D — в вершину E. Поэтому середина M отрезка

282 8 класс

A B

Рис. 345

Рис. 346

Рис. 347

B C

Рис. 348

CD переходит в середину N отрезка ED, а прямая AM — в

прямую BN . Следовательно, искомый угол равен 60

◦

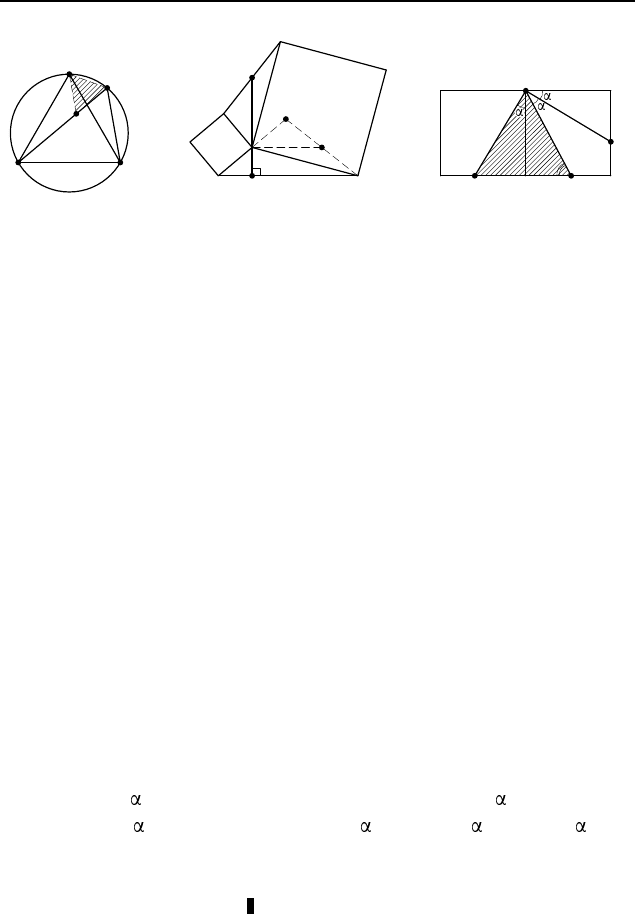
2.361. Заметим, что точка K — середина отрезка OC,

где O — центр данного правильного шестиугольника (рис. 345).

При повороте на 60

◦

относительно точки A, переводящем точ-

ку O в точку B, вершина F переходит в точку O, а вершина E —

в точку C. Поэтому середина M отрезка F E переходит в

середину K отрезка OC. Следовательно, треугольник AMK

равносторонний.

2.362. Указание. Примените поворот на 60

◦

относительно

данной точки.

2.363. Указание. Примените поворот на 90

◦

относительно

точки на одной из данных прямых.

2.364. Указание. Примените поворот на 90

◦

относительно

данной точки.

2.365. Указание. Пусть P

— образ точки P при поворо-

те на угол 60

◦

относительно вершины A данного треугольника

(рис. 346). Тогда P P

= AP , CP

= BP .

2.366. Указание. Докажите, что центр квадрата совпадает

с центром параллелограмма, и примените поворот на 90

◦

отно-

сительно этого центра.

2.367. Рассмотрим поворот на 60

◦

относительно точки C,

переводящий точку E в D (рис. 347). При этом повороте точ-

ка B перейдет в точку A. Следовательно, отрезок BE переходит

в отрезок DA, а середина P отрезка BE — в середину M отрез-

ка AD. Поэтому треугольник CP M равносторонний.

2.368. 60

◦

, 60

◦

, 60

◦

При повороте на 60

◦

по часовой стрел-

ке вокруг точки D (рис. 348) вершина B переходит в вершину C,

вершина A — в вершину B, луч BA — в луч CB, а так как

§ 2.6 283

Рис. 349

Рис. 350

A B

CD K

Рис. 351

CN = BC − BN = AB − AM = BM, то точка M перехо-

дит в точку N . Следовательно, треугольник M DN — равносто-

ронний.

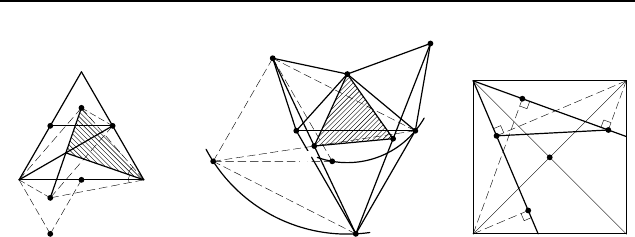
2.369. Пусть M

— образ точки M при повороте на 60

◦

относительно вершины B, переводящем C в A (рис. 349). То-

гда ∠AM

B+∠BM

M = ∠CMB+∠BM

M = 120

◦

+60

◦

= 180

◦

Поэтому точка M

лежит на отрезке AM. Следовательно,

AM = AM

+ M

M = BM + CM.

2.370. Рассмотрим поворот на 90

◦

относительно точки B,

переводящий вершину K в вершину N (рис. 350). При этом по-

вороте вершина C перейдет в вершину A, а точки A и E —

в некоторые точки A

и E

. Поскольку E

и B середины отрез-

ков A

N и A

C, то E

B — средняя линия треугольника A

NC.

Поэтому BE

k N C, а так как ∠EBE

= 90

◦

, то BE ⊥ NC.

Следовательно, точки E, B и F лежат на одной прямой.

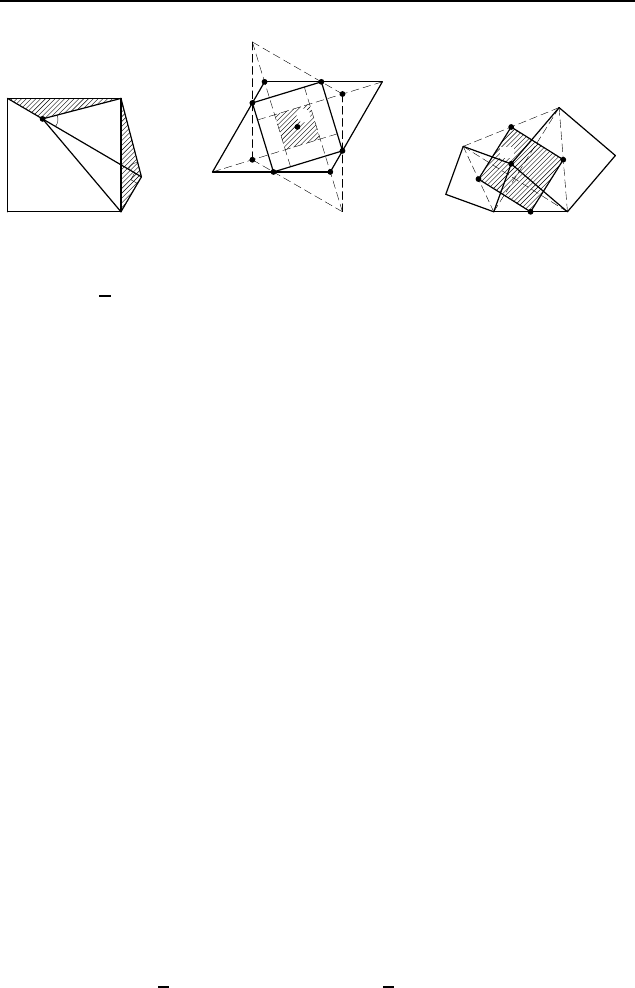
2.371. Повернем квадрат ABCD относительно вершины A

на 90

◦

так, чтобы вершина B перешла в вершину D (рис. 351).

Тогда точка M перейдет в точку M

, лежащую на продолжении

стороны CD за точку D, и M

D = BM. Обозначим ∠BAM =

= ∠MAK =

. Тогда ∠AM

D = ∠AMB = 90

◦

− , а ∠AKD =

= ∠BAK = 2

. Поэтому ∠M

AK = + (90

◦

−2 ) = 90

◦

− , т. е.

треугольник AKM

— равнобедренный. Следовательно, AK =

= KM

= KD + DM

= KD + BM.

2.372. 90

◦

, 60

◦

, 30

◦

Повернем треугольник BMP на 60

◦

относительно точки C так, чтобы точка B перешла в A

(рис. 352). Тогда точка P перейдет в точку P

отрез-

ка AC, точка M — в точку M

, лежащую вне треугольни-

ка ABC, точка D — в точку D

, центр треугольника AM

284 8 класс

Рис. 352

Рис. 353

A B

Рис. 354

Четырехугольник DP D

A — параллелограмм, DD

— его диа-

гональ. Поэтому D

D проходит через точку E и D

E = DE.

Поскольку CE — медиана равнобедренного треугольника DCD

(CD = CD

), то ∠CED = 90

◦

, а так как ∠DCD

= 60

◦

то ∠DCE = 30

◦

2.373. При повороте на 60

◦

относительно точки A (рис. 353),

переводящем точку C в точку B

, равносторонний треуголь-

ник A

BC переходит в равносторонний треугольник A

Поэтому B

= MA

= BA

и B

k BA

. Следовательно,

— параллелограмм. Поэтому середина P его диагона-

ли B

является серединой диагонали BA

. При рассматрива-

емом повороте отрезок C

переходит в отрезок BA

. Поэтому

середина Q отрезка C

переходит в середину P отрезка BA

Следовательно, треугольник AP Q равносторонний.

2.374. При повороте на 90

◦

вокруг центра O данного квад-

рата, переводящем вершину B в вершину A (рис. 354), верши-

на A переходит в вершину D, луч BK — в луч AK (∠ABK =

= ∠DAM), а луч AK — в луч DM. Поэтому точка K пересече-

ния лучей BK и AK перейдет в точку M пересечения лучей AM

и DM . Аналогично докажем, что при этом повороте точка L

перейдет в точку N . Следовательно, отрезок KL переходит в

отрезок MN . Поэтому KL = M N и KL ⊥ MN .

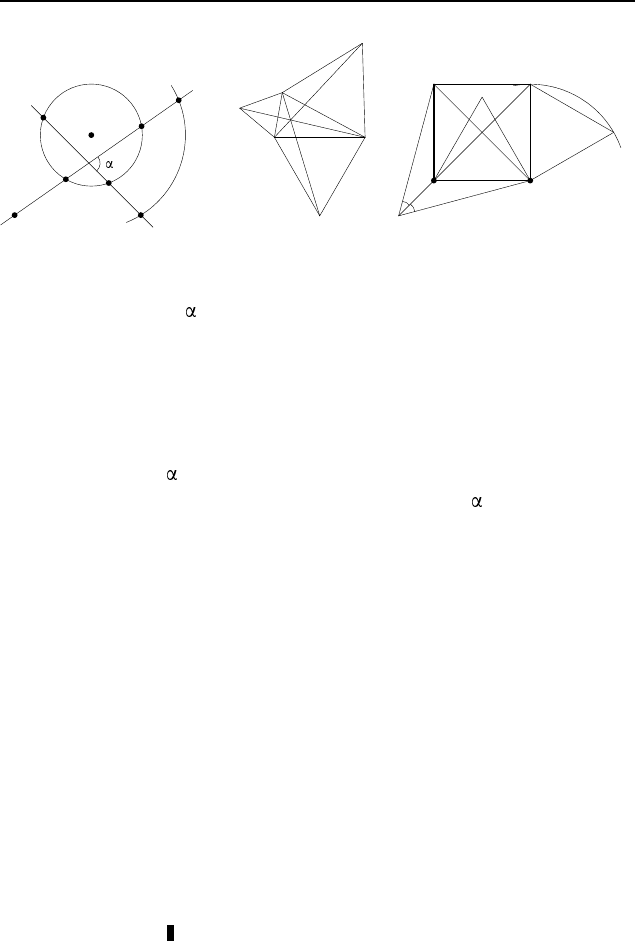
2.375. Предположим, что задача решена (рис. 355). Пусть

прямая l

, проходящая через точку A, пересекает данную

окружность в точках M и N, а прямая l

, проходящая че-

рез данную точку B, — в точках P и Q. Пусть также при

§ 2.6 285

Рис. 355

Рис. 356

B C

Рис. 357

повороте на угол

относительно центра данной окружности,

переводящем точку Q в точку N , точка P переходит в точку M.

Тогда прямая l

переходит в прямую l

, а точка B — в точку B

лежащую на прямой l

Отсюда вытекает следующий способ построения. Строим об-

раз B

точки B при повороте относительно центра окружности

на данный угол

. Тогда прямая AB

— одна из искомых пря-

мых. Проведя через точку B прямую под углом

к построенной,

получим вторую искомую прямую .

2.376. При повороте на угол 60

◦

относительно вершины A

(рис. 356), переводящем точку C

в B, точка C переходит в точ-

ку B

. Следовательно, отрезок C

C переходит в отрезок BB

Поэтому CC

= BB

. Аналогично докажем, что AA

= BB

2.377. Докажем, что при повороте на угол 60

◦

относительно

вершины D, переводящем точку K в точку C, образ вершины B

попадет на прямую AC (рис. 357). Тогда образы точек K, M и B

при этом повороте будут лежать на одной прямой AC. Возьмем

на продолжении диагонали AC за точку A такую точку P , для

которой ∠P DB = 60

◦

. Тогда ∠AP D = ∠CAD − ∠ADP = 45

◦

−

− 15

◦

= 30

◦

, а так как точка P равноудалена от точек B и D,

P C — биссектриса угла BP D. Поэтому ∠BP D = 60

◦

, значит,

треугольник BDP равносторонний. Следовательно, точка P —

образ точки B при этом повороте.

2.378. 135

◦

Будем считать, что AP = 1, BP = 2, CP = 3

(рис. 358). Пусть P

— образ точки P при повороте на 90

◦

против

часовой стрелки вокруг вершины B. Тогда P BP

— равнобед-

ренный прямоугольный треугольник. Поэтому ∠BP

P = 45

◦

286 8 класс

A B

Рис. 358

Рис. 359

A C

Рис. 360

P = 2

√

2. Следовательно, P P

= 8+1 = 9 = 3

= P C

Значит, треугольник P P

C прямоугольный, ∠P P

C = 90

◦

. Сле-

довательно, ∠AP B = ∠CP

B = ∠CP

P + ∠BP

P = 90

◦

+ 45

◦

= 135

◦

2.379. Пусть вершины F , E, M и N квадрата F EM N

лежат соответственно на сторонах AB, BC, CD и AD парал-

лелограмма ABCD (рис. 359). Достаточно доказать, что при

повороте на 90

◦

вокруг центра O квадрата F EMN указанные

перпендикуляры переходят друг в друга. Пусть параллело-

грамм A

— образ параллелограмма ABCD при этом

повороте (точка A

— образ точки A и т. д.). Поскольку стороны

параллелограмма A

перпендикулярны сторонам па-

раллелограмма ABCD, F A

⊥ BC и A

E ⊥ AB. Поэтому A

—

точка пересечения высот треугольника BEF и, следовательно,

⊥ EF . Значит, перпендикуляр, опущенный из вершины A

на сторону NF квадрата F EMN, переходит при рассматрива-

емом повороте в перпендикуляр, опущенный из вершины B на

сторону F E. Отсюда следует утверждение задачи.

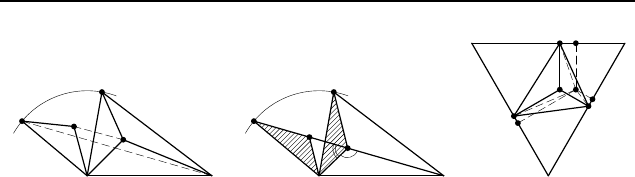
2.380. Пусть O

и O

— центры квадратов ABMN и BCP Q,

X и Y — середины отрезков MQ и AC соответственно (рис. 360).

При повороте на угол 90

◦

относительно точки B, переводя-

щем точку M в точку A, точка C переходит в точку Q, а

отрезок MC — в отрезок AQ. Следовательно, M C = AQ

и MC ⊥ AQ. Точки O

, X, O

и Y — середины сторон че-

тырехугольника AM QC. Поэтому O

Y — параллелограмм,

= O

Y =

MC, O

X = Y O

AQ, XO

k O

Y k MC,

X k Y O

k AQ. Следовательно, O

Y — квадрат.

§ 2.6 287

а)

б )

YBK M

в)

Рис. 361

2.381. Первый спо с об. Пусть P — некоторая точка внутри

остроугольного треугольника ABC (рис. 361, а). При повороте

на 60

◦

относительно вершины A треугольник ABP переходит в

равный ему треугольник AP

, а треугольник AP

P равносто-

ронний. Поэтому

P B + P A + P C = B

+ P

P + P C > B

причем равенство достигается только в случае, когда точки P

и P лежат на отрезке B

C. Тогда ∠AP C = 120

◦

, т. е. сторона AC

видна из точки P под углом 120

◦

(рис. 361, б ). Аналогично дока-

жем, что ∠AP B = 120

◦

. Следовательно, ∠BP C = 120

◦

. Таким

образом, каждая сторона треугольника видна из искомой точ-

ки P под углом 120

◦

. Поэтому для построения точки P доста-

точно построить на двух сторонах треугольника как на хордах

дуги, вмещающие углы 120

◦

Второй способ. Пусть P — точка, внутри треугольника

ABC, из которой все стороны видны под углом 120

◦

(рис. 361, в).

Через вершины A, B и C проведем прямые, перпендикулярные

отрезкам P A, P B и P C. Пусть M, N и K — точки пересече-

ния этих прямых. Тогда треугольник MNK равносторонний.

Если Q — произвольная точка внутри треугольника ABC, а X,

Y и Z — ее проекции на стороны KN, KM и M N треугольни-

ка MNK, проходящие соответственно через точки A, B и C,

то P A+P B +P C = QX +QY +QZ (каждая из этих сумм равна

высоте треугольника MNK). Поскольку QX 6 QA, QY 6 QB

и QZ 6 QC, то P A + P B + P C 6 QA + QB + QC.

2.384. Указание. Пусть MN — отрезок данной длины, па-

раллельный данной прямой l. Постройте образ луча BC при

288 8 класс

M N

S S

Рис. 362

Рис. 363

параллельном переносе, переводящем точку M в точку N (или

N в M).

2.385. Первый способ. Предположим, что искомая хорда AB

построена (рис. 362). Пусть MN — данный отрезок. Тогда

при параллельном переносе, переводящем точку M в точку N

(или N в M), точка A перейдет в точку B, а данная окруж-

ность S перейдет в окружность S

, проходящую через точку B.

Отсюда вытекает следующий способ построения. Строим об-

раз S

данной окружности при параллельном переносе, перево-

дящем точку M , в точку N . Точки пересечения окружностей S

и S

— концы искомых хорд.

Если окружности S

и S не пересекаются, то задача не имеет

решений.

Второй способ . Поскольку геометрическое место середины

всех хорд данной окружности, имеющих заданную длину, есть

окружность, концентрическая данной, то задача сводится к по-

строению касательной к этой окружности, параллельной данной

прямой.

2.386. Указание. Пусть MN — данный отрезок. Рассмот-

рите образ одной из окружностей при параллельном переносе,

переводящем точку M в точку N.

2.387. Указание. Рассмотрите образы отрезков AM и DM

при параллельном переносе, переводящем точку A в точку B.

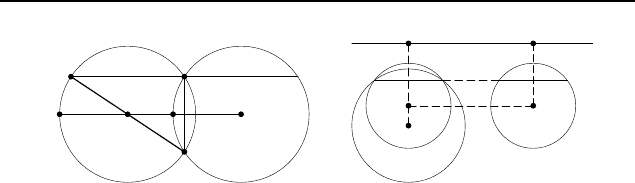
2.388. Пусть O

и O

— центры первой и второй окружно-

стей (рис. 363). Обозначим ∠AO

K =

. Из равнобедренного

треугольника AO

K находим, что ∠AKO

= 90

◦

−

. Поэтому

∠BKO

= 180

◦

− 90

◦

−



◦

−



, ∠KO

B = 180

◦

−

Следовательно, пря мые O

A и O

B параллельны. При парал-

§ 2.6 289

Рис. 364

O O

Рис. 365

лельном переносе, переводящем точку O

в точку O

, первая

окружность перейдет во вторую, а точка A перейдет в точку B.

Следовательно, AB = O

= 2R.

2.389. Пусть O

и O

— центры данных окружностей S

и S

(рис. 364), точка A лежит на окружности S

, B — на окружно-

сти S

, B — между A и O

. Через точку M проведем прямую,

параллельную O

. Пусть D — ее точка пересечения с окруж-

ностью S

. При параллельном переносе, переводящем точку O

в точку O

, окружность S

перейдет в окружность S

, точка D —

в точку M, точка A — в точку B. Поэтому отрезок DM равен и

параллелен отрезку AB, а ∠DMN = 90

◦

. Тогда DN — диаметр

окружности. Следовательно, 4R

= DN

= DM

+ MN

= AB

+ M N

2.391. Предположим, что нужная прямая проведена

(рис. 365). Пусть AB = CD — хорды данных окружностей S

и S

, параллельные данной прямой l, Q

и Q

— проекции

центров O

и O

этих окружностей на прямую l. Тогда при

параллельном переносе, переводящ ем точку Q

в точку Q

отрезок AB перейдет в отрезок CD, а окружность S

— в

окружность S, имеющую общую хорду CD с окружностью S

Отсюда вытекает следующий способ построения. Опустим

перпендикуляры из центров данных окружностей S

и S

на

данную прямую l. Пусть Q

и Q

— основания этих перпендику-

ляров. Если при параллельном переносе, переводящем точку Q

в точку Q

, образ S окружности S

пересекает окружность S

в двух точках C и D, то CD — искомая прямая.

2.392. Рассмотрим случай, когда в четырехугольнике нет

параллельных сторон. Пусть пересекаются лучи BA и CD

290 8 класс

Рис. 366

Рис. 367

Рис. 368

(рис. 366). Предположим, что нужный четырехугольник ABCD

построен. Пусть B

— образ вершины B при параллельном пе-

реносе, переводящем точку A в точку D. Тогда DB

= AB.

Поэтому в треугольнике DB

C известны две стороны (DB

= a,

DC = b) и угол между ними (∠B

DC = ∠ADC − ∠ADB

= ∠ADC − (180

◦

− ∠DAB)).

Отсюда вытекает следующий способ построения. Строим

треугольник DB

C. Затем в полуплоскости, содержащей точ-

ку B

, откладываем от лучей DC и CD углы CDX и DCY ,

соответственно равные данным углам D и C. Затем через

точку B

проводим прямую, параллельную прямой DX. Эта

прямая пересекает прямую CY в искомой вершине B, а пря-

мая, проходящая через точку B параллельно DB

, пересекает

прямую DX в искомой вершине A.

2.394. Рассмотрим случай, когда даны две противополож-

ные стороны (рис. 367). Предположим, что нужный четырех-

угольник ABCD построен. Пусть AB = a и CD = b — данные

стороны, AC = d

, BD = d

— данные диагонали, K — точка

пресечения диагоналей, ∠BKC =

— данный угол. Достро-

им треугольники DAC и BAC до параллелограммов ADD

и ABB

C. Тогда BB

D — также параллелограмм со сторо-

нами B

= BD = d

, BB

= DD

= AC = d

и у глом

между

сторонами DD

и DB. При этом точка C удалена от вершин D

и B

на расстояния b и a соответственно.

Отсюда вытекает следующий способ построения. Строим па-

раллелограмм BB

D по двум соседним сторонам DD

= d

DB = d

и углу ∠BDD

. Пересечение окружностей с цен-

трами в точках B

и D с радиусами a и b соответственно дает