Гордин Р.К. Геометрия. Планиметрия. 7-9 классы
Подождите немного. Документ загружается.


§ 2.6 291
вершину C. Через точки B и D проведем прямые, параллель-
ные CB
1
и CD
1
соответственно. Пересечение этих прямых дает
искомую вершину A.
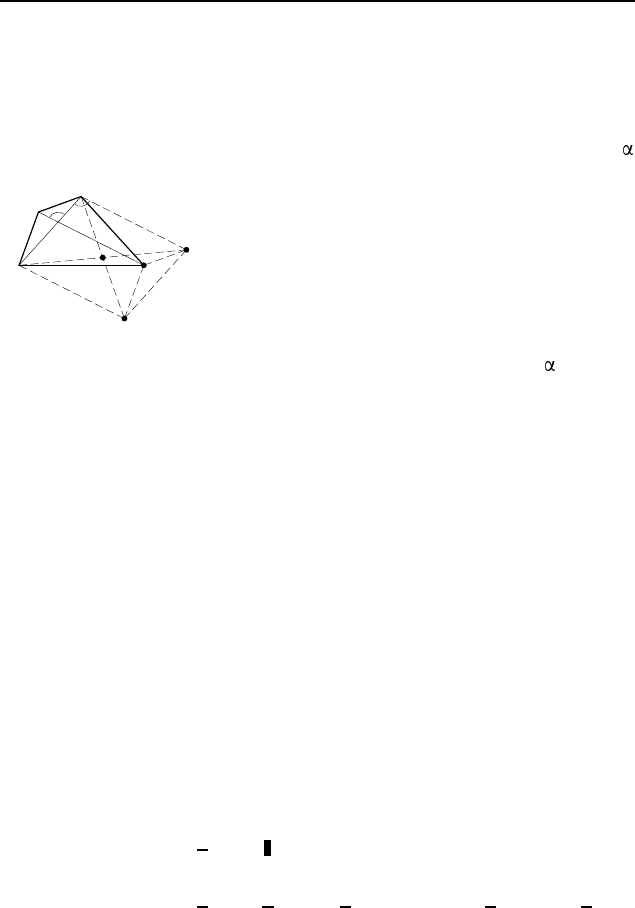
2.395. Предположим, что четырехугольник ABCD постро-
ен (рис. 368). Пусть M и N — середины противоположных сто-
рон BC и AD, AB = a, BC = b, CD = c, AD = d, MN = m —
данные отрезки. Достроим треугольники ABM и DCM до па-
раллелограммов ABMM
1
и DCMM
2
. Тогда MM
1
= AB = a,
MM
2
= CD = c. Из равенства треугольников AM
1
N и DM
2
N
следует, что точки M
1
, N и M
2
лежат на одной прямой и M N —
медиана треугольника M
1
MM
2
.
Отсюда вытекает следующий способ построения. Строим
треугольник M
1
MM
2
по двум сторонам и медиане, проведен-
ной к третьей. Пусть N — середина M
1
M
2
. На основаниях NM
1
и NM
2
строим треугольники M
1
NA и M
2
ND с боковыми сто-
ронами, равными
b
2
и
d
2
, так, что точки A и D лежат по разные
стороны от прямой M
1
M
2
. Через точки A, M и D проводим
прямые, параллельные MM
1
, AM
1
и MM
2
соответственно.
Первая и третья из этих прямых пересекают вторую в искомых
вершинах B и C.
2.396. Пусть O(a; b) и Q(c; d) — центры симметрий,
M(x; y) — произвольная точка плоскости. При симметрии отно-
сительно точки O точка M переходит в точку N(a − x; b − y),
а при симметрии относительно точки Q точка N переходит в
точку L(c − (a − x); d − (b − y)). Таким образом, при компо-
зиции этих симметрий произвольная точка M(x; y) перешла в
точку L(x − a + c; y − b + d). Следовательно, это параллель-
ный перенос. Заметим, что результат не зависит от порядка
применения симметрий.
2.397. Пусть в выбранной системе координат данные парал-
лельные оси симметрии имеют уравнения x = a и x = b. Тогда
при симметрии относительно первой прямой точка M(x; y) пе-
реходит в точку N(2a − x; y), а при симметрии относительно
второй прямой точка N переходит в точку L(2b − (2a − x); y).
Таким образом, при композиции этих симметрий произвольная
точка M(x; y) перешла в точку L(x −2a + 2b; y). Следовательно,
292 8 класс
это параллельный перенос в направлении, перпендикулярном
осям симметрий, на расстояние, равное 2|a − b|. Заметим, что
результат не зависит порядка применения симметрий.
2.398. Пусть диагонали AC и BD четырехугольника ABCD
N
D
A
B
C
K
M
Рис. 369
равны соответственно a и b, а угол между ними равен
(рис. 369). При параллельном переносе,
переводящем точку B в точку A, диа-
гональ BD переходит в отрезок AM;
при параллельном переносе, переводя-
щем точку B в точку C, диагональ BD
переходит в отрезок CK. Тогда четы-
рехугольник ACKM — параллелограмм
со сторонами a и b и углом
между
ними. Если N — точка пересечения диагоналей AK и CM
этого параллелограмма, то
AB + BC + CD + AD = DM + DK + DC + DA =
= (DM +DC)+(DK+DA) > CM +AK = NC+NM+NA+NK.
Следовательно, вершина D искомого четырехугольника ABCD
минимального периметра должна совпасть с точкой N. Парал-
лелограмм ACKM можно построить по двум сторонам и у глу
между ними. Тогда A и C — вершины искомого четырехуголь-
ника, вершина D есть точка пересечения диагоналей этого па-
раллелограмма, а четвертая вершина B — образ точки D при
параллельном переносе, переводящем точку K в точку C.
§ 2.7
2.401.
# »
MN = −
2
5
# »
CB.
Имеем:
# »
MN =
# »
AN−
# »
AM =
2
5
# »
AC−
2
5
# »
AB =
2
5
(
# »
AC−
# »
AB) =
2
5
# »
BC = −
2
5
# »
CB.
2.402. D(9; 0),
# »
AC(2; 3),
# »
BD(14; −1).
2.403.
# »
AB(3; 3),
# »
DC(3; 3),
# »
AD(5; −5),
# »
BC(5; −5),
# »
AC(8; −2),
# »
BD(2; −8).
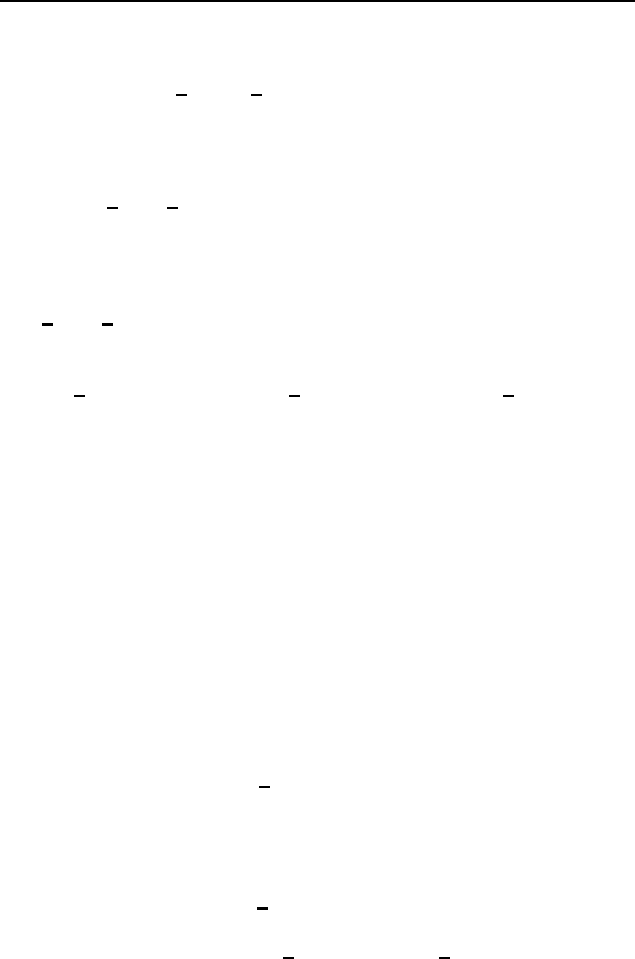
§ 2.7 293
2.404. Указание. Найдите координаты и абсолютные вели-
чины векторов
# »
AB,
# »
DC,
# »
AD,
# »
BC,
# »
AC,
# »
BD.
2.405.
# »
AM =
3
4
# »
AC −
1
4
# »
BD.
2.406
0
. Указание. Сложите почленно равенства
# »
OM =
# »
OA +
# »
AM и
# »
OM =
# »
OB +
# »
BM.
2.407.
5
7
#»
a +
2
7
#»
b . Указание.
# »
AM =
# »
AB +
# »
BM,
# »
AM =
# »
AC +
# »
CM.
2.408.
# »
AD = 2
#»
a + 2
#»
b ,
# »
BD =
#»
a + 2
#»
b ,
# »
F D = 2
#»
a +
#»
b ,
# »
BM =
= −
1
2
#»
a +
3
2
#»
b .
2.409. Указание.
# »
AA
1
=
1
2
(
# »
AB +
# »
AC),
# »
BB
1
=
1
2
(
# »
BA +
# »
BC),
# »
CC
1
=
1
2
(
# »
CA +
# »
CB).
2.410. Указание. Пусть AA
1
, BB
1
, CC
1
— медианы тре-
угольника ABC. Тогда
# »
AA
1
+
# »
BB
1
+
# »
CC
1
=
#»
0 .
2.411. Указание.
# »
M
1
M
2
+
# »
M
3
M
4
+
# »
M
5
M
6
=
#»
0 .
2.412. Указание.
# »
OA
1
−
# »
OA =
# »
AA
1
.
2.413
0
. Указание.
# »
MM
1
=
# »
MA+
# »
AA
1
+
# »
A
1
M
1
,
# »
MM
1
=
# »
MB+
+
# »
BB
1
+
# »
B
1
M
1
.
2.414
0
. Указание. Пусть AA
1
, BB
1
и CC
1
— медианы тре-
угольника ABC. Тогда
# »
AA
1
+
# »
BB
1
+
# »
CC
1
=
#»
0 .
2.415. Пусть K — точка пересечения медиан треугольни-
ка ABC. Тогда
# »
MK =
1
3
(
# »
MA +
# »
MB +
# »
MC) =
#»
0 , поэтому
точки K и M совпадают.
2.416. M(1; 2). Указание. Пусть O — начало координат, M —
точка пересечения медиан треугольника ABC. Тогда
# »
OM =
1
3
(
# »
OA +
# »
OB +
# »
OC).
2.417. Указание.
# »
OM =
1
2
(
# »
OA +
# »
OC) =
1
2
(
# »
OB +
# »
OD).
2.418
0
. Пусть A
1
, B
1
, C
1
— середины сторон BC, AC и AB
треугольника ABC, P
1
, Q
1
, R
1
— середины сторон QR, P R и RQ
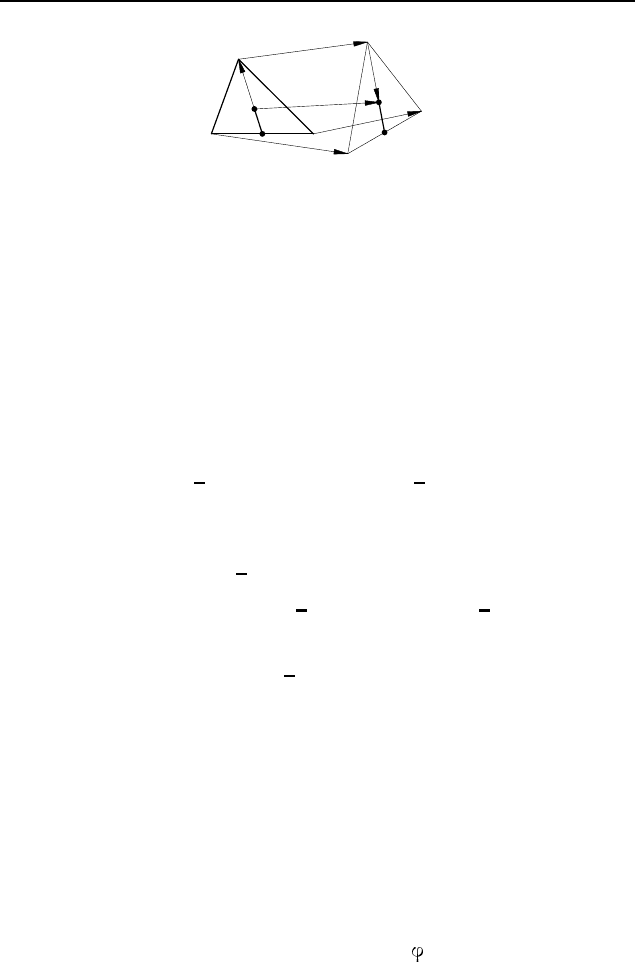
294 8 класс
B
A
A
1
C
M
N
P
P
1
Q
R
Рис. 370
треугольника P QR (рис. 370). Сложим почленно следующие
векторные равенства:
# »
MN =
# »
MA +
# »
AP +
# »
P N,
# »
MN =
# »
MB +
# »
BQ +
# »
QN,
# »
MN =
# »
MC +
# »
CR +
# »
RN.
Получим:
3
# »
MN = (
# »
AP +
# »
BQ+
# »
CR)+(
# »
MA+
# »
MB+
# »
MC)+(
# »
P N +
# »
QN+
# »
RN) =
=
# »
AP +
# »
BQ+
# »
CR−
2
3
(
# »
AA
1
+
# »
BB
1
+
# »
CC
1
)+
2
3
(
# »
P P
1
+
# »
QQ
1
+
# »
RR
1
) =
=
# »
AP +
# »
BQ +
# »
CR −
#»
0 +
#»
0 =
# »
AP +
# »
BQ +
# »
CR.
Следовательно,
# »
MN =
1
3
(
# »
AP +
# »
BQ +
# »
CR).
2.419. Указание.
# »
OO
1
=
1
2
(
# »
AA
1
+
# »
CC
1
) =
1
2
(
# »
BB
1
+
# »
DD
1
).
2.420. Указание. Если P — середина отрезка AB, то
# »
OP =
1
2
(
# »
OA +
# »
OB).
2.421. Указание. Найдите координаты векторов
# »
AC и
# »
BD и
вычислите скалярное произведение
# »
AC ·
# »
BD.
2.422. Указание. Пусть четырехугольник ABCD — ромб.
Обозначим
# »
AB =
#»
a ,
# »
AD =
#»
b . Тогда
# »
AC =
#»
a +
#»
b ,
# »
BD =
#»
b −
#»
a .
2.423. D(4; 4). Указание. Обозначьте через t абсциссу точ-
ки D, найдите координаты векторов
# »
BC и
# »
AD и решите урав-
нение
# »
BC ·
# »
AD = 0 относительно t.
2.424. Указание. Воспользуйтесь равенством
#»
a ·
#»
b = |
#»
a |· |
#»
b | · cos
.
2.425. Указание. Обозначьте AK : KB = AN : ND = k и
выразите векторы
# »
KL и
# »
NM через векторы
# »
AB и
# »
AD.

§ 2.7 295
O
A B
CD
M N
Рис. 371
MN
A
B C
D
P
Q
R
S
Рис. 372
2.426. Указание. Выразите векторы
# »
KN ,
# »
MF и
# »
GL через
векторы
# »
AL,
# »
CM и
# »
CF и найдите сумму
# »
KN +
# »
MF +
# »
GL.
2.427. Пусть M и N такие точки, что
# »
OM =
# »
OA +
# »
OD
и
# »
ON =
# »
OB +
# »
OC (рис. 371). Поскольку
# »
OA +
# »
OB +
# »
OC +
+
# »
OD =
#»
0 , то
# »
OM = −
# »
ON, т. е.
# »
OM и
# »
ON — противопо-
ложные векторы. Поэтому точки M , O и N лежат на одной
прямой. Поскольку четырехугольники OAMD и OBNC — ром-
бы, AD ⊥ MN и BC ⊥ MN, поэтому AD k BC. Аналогично
докажем, что AB k CD. Значит, четырехугольник ABCD —
параллелограмм, вписанный в окружность, т. е. прямоугольник.
2.428. В точке, из которой каждая из сторон треугольника
видна под углом 120
◦
(точка Торричелли, см. задачу 2.381).
2.429. Пусть точки P , Q, R, S принадлежат соответственно
сторонам AB, BC, CD, DA параллелограмма ABCD (рис. 372)
и AP : P B = BQ : QC = CR : RD = DS : SA = k. Тогда
# »
P Q =
# »
P B +
# »
BQ =
1
k + 1
# »
AB +
k
k + 1
# »
BC,
# »
SR =
# »
SD +
# »
DR =
k
k + 1
# »
AD +
1
k + 1
# »
DC =
k
k + 1
# »
BC +
1
k + 1
# »
AB.
Поэтому
# »
P Q =
# »
SR. Следовательно, P QRS — параллелограмм.
Пусть теперь M и N — точки пересечения диагоналей паралле-
лограммов ABCD и P QRS. Тогда
# »
MN =
1
4
(
# »
AP +
# »
BQ +
# »
CR +
# »
DS) =
=
1
4
k
k + 1
# »
AB +
k
k + 1
# »
BC +
k
k + 1
# »
CD +
k
k + 1
# »
DA
=
=
k
4(k + 1)
# »
AB +
# »
BC +
# »
CD +
# »
DA
=
k
4(k + 1)
·
#»
0 =
#»
0 .
Следовательно, точки M и N совпадают.
296 8 класс
M
N
A
B C
P
Q
R
Рис. 373
O
B
2
K
2
B
1
M
A
A
1
A
2
B C
C
1
C
2
K
1
K
3
Рис. 374
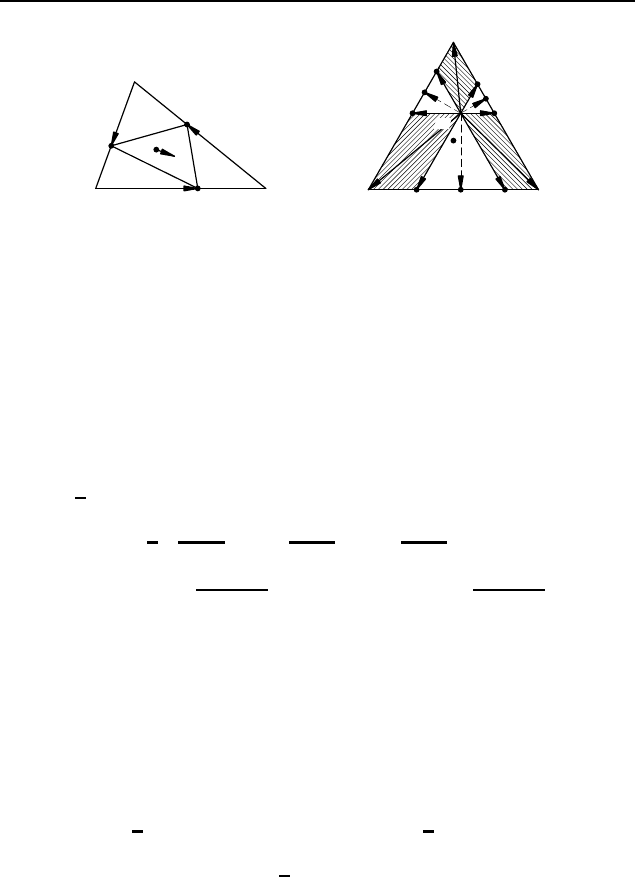
2.430. Пусть точки P , Q, R принадлежат сторонам тре-
угольника ABC и
AP : P B = BQ : QC = CR : RA = k
(рис. 373). Если M и N — точки пересечения медиан треуголь-
ников ABC и P QR соответственно, то
# »
MN =
1
3
(
# »
AP +
# »
BQ +
# »
CR) =
=
1
3
k
k + 1
# »
AB +
k
k + 1
# »
BC +
k
k + 1
# »
CA
=
=
k
3(k + 1)
(
# »
AB +
# »
BC +
# »
CA) =
k
3(k + 1)
·
#»
0 =
#»
0 .
Следовательно, точки M и N совпадают.
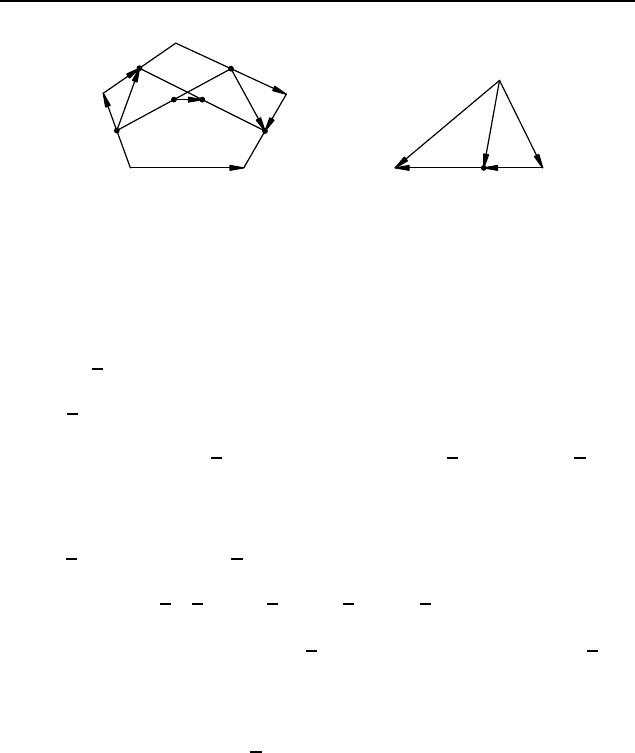
2.431. Проведем через точку M прямые, параллельные сто-
ронам треугольника, и обозначим точки пересечения этих пря-
мых со сторонами треугольника, как показано на рисунке 374.
Тогда K
1
, K
2
, K
3
— середины отрезков A
1
A
2
, B
1
B
2
, C
1
C
2
соот-
ветственно. Поэтому
# »
MK
1
=
1
2
(
# »
MA
1
+
# »
MA
2
),
# »
MK
2
=
1
2
(
# »
MB
1
+
# »
MB
2
),
# »
MK
3
=
1
2
(
# »
MC
1
+
# »
MC
2
).
Кроме того,
# »
MC
1
+
# »
MB
2
=
# »
MA,
# »
MC
2
+
# »
MA
1
=
# »
MB,
# »
MA
2
+
# »
MB
1
=
# »
MC.
§ 2.7 297
P Q
A
B
C
D
E
K
L
M
N
Рис. 375
O
A BC
Рис. 376
Тогда
# »
MK
1
+
# »
MK
2
+
# »
MK
3
=
=
1
2
(
# »
MA
1
+
# »
MA
2
+
# »
MB
1
+
# »
MB
2
+
# »
MC
1
+
# »
MC
2
) =
=
1
2
((
# »
MC
1
+
# »
MB
2
) + (
# »
MC
2
+
# »
MA
1
) + (
# »
MA
2
+
# »
MB
1
)) =
=
1
2
(
# »
MA +
# »
MB +
# »
MC) =
1
2
· 3 ·
# »
MO =
3
2
# »
MO.
2.432. Имеем:
# »
P Q =
1
2
(
# »
MK +
# »
NL) =
1
2
(
# »
MB +
# »
BK +
# »
ND +
# »
DL) =
=
1
2
1
2
# »
AB +
1
2
# »
BC +
1
2
# »
CD +
1
2
# »
DE
=
=
1
4
(
# »
AB +
# »
BC +
# »
CD +
# »
DE) =
1
4
# »
AE
(рис. 375). Следовательно,
P Q =
1
4
AE и P Q k AE.
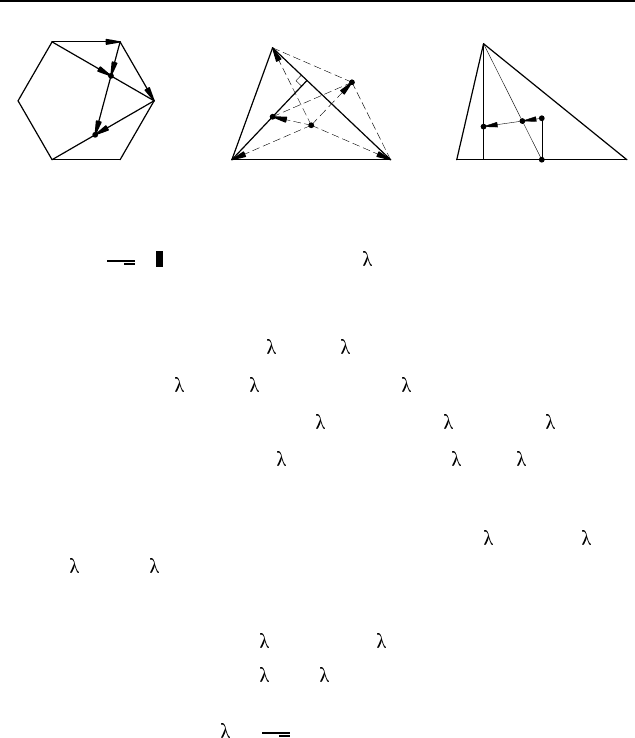
2.433. Достаточность. Если
# »
OC = k
# »
OA + (1 − k)
# »
OB,
то
# »
OC −
# »
OB = k(
# »
OA −
# »
OB), или
# »
BC = k
# »
BA (рис. 376). Следо-
вательно, векторы
# »
BC и
# »
BA коллинеарны. Поэтому точки A,
B и C принадлежат одной прямой.
Необходимость. Если точки A, B, C принадлежат одной
прямой, то векторы
# »
BC и
# »
BA коллинеарны. Поэтому найдется
число k такое, что
# »
BC = k
# »
BA. Тогда
# »
OC −
# »
OB = k(
# »
OA −
# »
OB), или
# »
OC = k
# »
OA + (1 − k)
# »
OB.
298 8 класс
#»
a
#»
b
A B
C
DE
F
M
N
Рис. 377
O
A
BC
K
M
Рис. 378
O
A
BC
H
M
Рис. 379
2.434.
1
√
3
. Заметим, что 0 6 6 1. Обозначим
# »
AB =
#»
a ,
# »
BC =
#»
b (рис. 377). Тогда
# »
AM =
# »
AC = (
#»
a +
#»
b ),
# »
CN =
# »
CE = (
# »
CF +
# »
F E) = (−2
#»
a +
#»
b ),
# »
BM =
# »
BA +
# »
AM = −
#»
a +
(
#»
a +
#»
b ) = ( − 1)
#»
a +
#»
b ,
# »
BN =
# »
BC +
# »
CN =
#»
b +
(−2
#»
a +
#»
b ) = −2
#»
a + (
+ 1)
#»
b .
Если точки B, M , N лежат на одной прямой, то векторы
# »
BM
и
# »
BN коллинеарны. Поэтому
# »
BM = k
# »
BN, или ( −1)
#»
a +
#»
b =
= −2k
#»
a + k(
+ 1)
#»
b . Поскольку
#»
a и
#»
b — неколлинеарные
векторы, имеем систему уравнений:
(
− 1 = −2k ,
= k( + 1).
Отсюда находим, что =
1
√
3
.
2.435. Рассмотрим сумму векторов
# »
OA +
# »
OB =
# »
OK
(рис. 378). Отрезок OK — диагональ ромба OAKB. Поэто-
му OK перпендикулярно AB. Следовательно, OK k CH. Тогда
если
# »
OK +
# »
OC =
# »
OM, то точка M принадлежит высоте,
проходящей через вершину C. Таким образом, если
# »
OA +
+
# »
OB +
# »
OC =
# »
OM, то точка M принадлежит каждой высоте
треугольника ABC. Следовательно, точки M и H совпадают.
2.436. Пусть O, H и M — соответственно центр описан-
ной окружности, ортоцентр и точка пересечения медиан тре-
угольника ABC (рис. 379). Тогда
# »
OH =
# »
OA +
# »
OB +
# »
OC (см.
§ 2.7 299
A
B C
K
M
P
Рис. 380
#»
a
#»
b
A
B C
D
Рис. 381
A
A
1
B
C
C
1
H
Рис. 382
задачу 2.435) и
# »
OM =
1
3
(
# »
OA +
# »
OB +
# »
OC) (см. задачу 2.414
0
).
Поэтому
# »
OM =
1
3
# »
OH. Следовательно, точки O, M и H лежат
на одной прямой, причем точка M делит отрезок OH в отноше-
нии 1 : 2, считая от точки O.
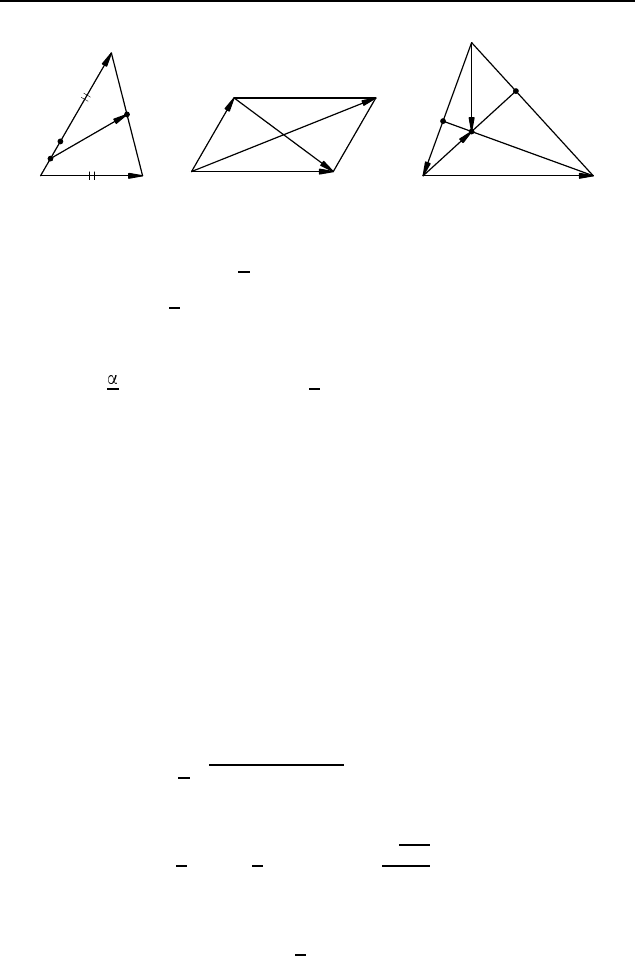
2.437.
2
. Указание.
# »
P M =
1
2
(
# »
KA+
# »
BC) (см. задачу 2.413
0
),
а абсолютные величины векторов KA и BC равны между собой
(рис. 380).
2.438. K(5; −3). Указание. Пусть M — середина AB,
K(x; y) — искомая точка на данной прямой. Тогда
# »
KM ·
# »
AB = 0.
2.439. Указание. Применяя свойства скалярного произведе-
ния векторов, докажите, что скалярное произведение данного
вектора на вектор
#»
c равно 0.
2.440. Пусть четырехугольник ABCD — параллелограмм
(рис. 381). Обозначим
# »
AB =
#»
a ,
# »
AD =
#»
b . Тогда
# »
AC =
#»
a +
#»
b ,
# »
BD =
#»
b −
#»
a ,
# »
AC
2
=
#»
a
2
+
#»
b
2
+ 2
#»
a ·
#»
b ,
# »
BD
2
=
#»
a
2
+
#»
b
2
− 2
#»
a ·
#»
b .
Следовательно, AC
2
+ BD
2
= 2a
2
+ 2b
2
= 2AB
2
+ 2AD
2
.
2.441. m =
1
2
√
2b
2
+ 2c
2
− a
2
. Указание. Достройте тре-
угольник до параллелограмма и воспользуйтесь результатом
предыдущей задачи.
2.442.
# »
AM =
2
5
# »
AB +
3
5
# »
AC; AM =
√
790
5
.
2.443. Указание. Выразите векторы
# »
KM и
# »
DM через век-
торы
# »
AB и
# »
AD и найдите скалярное произведение
# »
KM ·
# »
DM.
2.444. Указание.
# »
AP =
1
2
(
# »
AB +
# »
AC),
# »
ML =
# »
AL −
# »
AM,
угол между векторами
# »
AB и
# »
AL равен углу между векторами
# »
AC и
# »
AM.

300 8 класс
2.445. Имеем:
# »
AB ·
# »
CD +
# »
BC ·
# »
AD +
# »
CA ·
# »
BD =
= (
# »
AC +
# »
CB)(
# »
CA +
# »
AD) +
# »
BC ·
# »
AD +
# »
CA ·
# »
BD =
= −
# »
AC
2
+
# »
AC ·
# »
AD +
# »
CB ·
# »
CA +
# »
CB ·
# »
AD +
# »
BC ·
# »
AD +
# »
CA ·
# »
BD =
= (−
# »
AC
2
+
# »
CB ·
# »
CA+
# »
CA·
# »
BD)+(
# »
AC ·
# »
AD+
# »
CB ·
# »
AD+
# »
BC·
# »
AD) =
=
# »
AC(−
# »
AC −
# »
CB −
# »
BD) +
# »
AD(
# »
AC +
# »
CB +
# »
BC) =
= −
# »
AC ·
# »
AD +
# »
AD ·
# »
AC = 0.
2.446. Пусть высоты AA
1
и CC
1
треугольника ABC пересе-
каются в точке H (рис. 382). Докажем, что прямая BH перпен-
дикулярна стороне AC. Тогда третья высота BB
1
также пройдет
через точку H. Действительно,
# »
BH ·
# »
AC = (
# »
BA +
# »
AH)(
# »
AB +
# »
BC) =
= −AB
2
+
# »
BA ·
# »
BC +
# »
AH ·
# »
AB +
# »
AH ·
# »
BC =
= −AB
2
+
# »
BA ·
# »
BC +
# »
AH ·
# »
AB + 0 =
=
# »
AB(
# »
AH −
# »
AB −
# »
BC) =
# »
AB(
# »
AH −
# »
AC) =
# »
AB ·
# »
CH = 0.
Что и требовалось доказать.
2.447. Имеем:
# »
AH ·
# »
BC = (
# »
AO +
# »
OH)(
# »
OC −
# »
OB) =
= (
# »
AO +
# »
OA +
# »
OB +
# »
OC)(
# »
OC −
# »
OB) =
= (
# »
OB +
# »
OC)(
# »
OC −
# »
OB) =
# »
OC
2
−
# »
OB
2
= 0.
Поэтому AH ⊥ BC. Аналогично, BH ⊥ AC и CH ⊥ AB. Сле-
довательно, H — точка пересечения высот треугольника ABC.
2.448. См. рисунок 383.
# »
CD =
AD
AB
·
# »
CB +
BD
AB
·
# »
CA (см.
пример 1 из §2.7, с. 108), поэтому
CD
2
=
AD
AB
2
·
# »
CB
2
+
BD
AB
2
·
# »
CA
2
+ 2
AD
AB
·
BD
AB
·
# »
CB ·
# »
CA,
но
# »
AB =
# »
CB−
# »
CA, значит,
# »
AB
2
=
# »
CB
2
+
# »
CA
2
−2
# »
CB ·
# »
CA, откуда
2
# »
CB ·
# »
CA = CB
2
+ CA
2
−AB
2
.
