Graef M. Introduction to conventional transmission electron microscopy
Подождите немного. Документ загружается.

48 Basic crystallography
1.7.1 Transformation rules
Let us consider two crystallographic reference frames, {a
1
, a
2
, a
3
} and {a
1
, a
2
, a
3
}.
In general, the relation between the two sets of basis vectors can be written as
a
1
= α
11
a
1
+ α
12
a
2
+ α
13
a
3
;
a
2
= α
21
a
1
+ α
22
a
2
+ α
23
a
3
;
a
3
= α
31
a
1
+ α
32
a
2
+ α
33
a
3
.
(1.43)
This is a linear relation, known as a coordinate transformation. We will assume
throughout this book that the origin itself does not change during the coordinate
transformation. If there were a change in the position of the origin as well, then we
would need to add a translation vector to the equations above.
The nine numbers α
ij
can be grouped as a square matrix:
α
ij
=
α
11
α
12
α
13
α
21
α
22
α
23
α
31
α
32
α
33
, (1.44)
and the transformation equations can be rewritten in short form as
a
i
= α
ij
a
j
. (1.45)
The inverse transformation must also exist and is described by the inverse of the
matrix α
ij
:
a
i
= α
−1
ij
a
j
. (1.46)
Consider the position vector p. This vector is independent of the reference frame,
and has components in both the unprimed and primed reference frames. We must
have the following relation:
p = p
i
a
i
= p
j
a
j
. (1.47)
Using the inverse coordinate transformation we can rewrite the first equality as
p
i
a
i
= p
i
α
−1
ij
a
j
,
and after comparison with the last equality of equation (1.47) we find
p
j
= p
i
α
−1
ij
. (1.48)
Note the order of the indices of the matrix α; the summation index is the index i,
which means that we must premultiply the matrix by the row vector p
i
. Similarly,
one can readily show that
p
i
= p
j
α
ji
. (1.49)
1.7 Coordinate transformations 49
We interpret equations (1.48) and (1.49) as follows: the vector p is independent of
the chosen reference frame if its components with respect to two different refer-
ence frames are related to each other by equations (1.48) and (1.49). This relation
obviously also holds for direction vectors [uvw], since they are a special case of
position vectors p (integer components instead of rational ones).
It is now straightforward to derive the transformation relation for the direct metric
tensor:
g
ij
= a
i
· a
j
;
= α
ik
a
k
· α
jl
a
l
;
= α
ik
α
jl
a
k
· a
l
,
and hence
g
ij
= α
ik
α
jl
g
kl
. (1.50)
The inverse relation is given by
g
ij
= α
−1
ik
α
−1
jl
g
kl
. (1.51)
One can use these relations to define a second-rank tensor: any mathematical quan-
tity h
ij
which satisfies the above transformation rules is a second-rank tensor. Sim-
ilarly, any mathematical quantity p
i
, satisfying the transformation rules (1.48) and
(1.49), is a vector. It is straightforward to extend these definitions to higher-order
tensors, but we will not need them in this book. For a detailed overview of tensor
calculus we refer to [Wre72].
Next, we will derive the transformation relations for quantities in reciprocal
space. We have already seen that if the components of a vector p are known in
direct space, then its components in the reciprocal reference frame are given by
p
∗
i
= g
ij
p
j
.
Using equation (1.49) we have
p
∗
i
= g
ij
α
kj
p
k
. (1.52)
From equation (1.51) we find, after multiplying both sides of the equation by α
kj
,
g
ij
α
kj
= α
−1
il
g
lk
,
and substitution in equation (1.52) leads to
p
∗
i
= α
−1
il
g
lk
p
k
,
= α
−1
il
p
∗
l
,
50 Basic crystallography
where we have once again used the properties of the direct metric tensor. The
components of a vector in reciprocal space thus transform as follows:
p
∗
i
= α
−1
il
p
∗
l
, (1.53)
and the inverse relation is given by
p
∗
l
= α
li
p
∗
i
. (1.54)
In particular, these equations are valid for the reciprocal lattice vectors g.
The reciprocal basis vectors satisfy similar transformation relations, which are
derived as follows:
g = g
∗
i
a
∗
i
= g
∗
l
a
∗
l
,
= α
li
g
∗
i
a
∗
l
,
from which we find:
a
∗
i
= a
∗
l
α
li
. (1.55)
The corresponding inverse relation is given by
a
∗
i
= a
∗
j
α
−1
ji
. (1.56)
Finally, it is again easy to show that the reciprocal metric tensor transforms accord-
ing to the rules
g
∗
ij
= α
ki
α
lj
g
∗
kl
, (1.57)
and
g
∗
ij
= α
−1
ki
α
−1
lj
g
∗
kl
. (1.58)
The transformation rules derived in this section are summarized in Table 1.6.
All that is required to carry out any coordinate transformation is the matrix α
ij
,
expressing the new basis vectors in terms of the old ones. The relations in Table 1.6
require, in addition to α
ij
, the inverse α
−1
ij
and transpose α
T
ij
matrices, and the trans-
pose of the inverse matrix (α
−1
ij
)
T
. These transformation rules seem easy enough,
but one must actually pay close attention to the indices in order to avoid mistakes.
In the following subsection we will illustrate coordinate transformations by means
of a few examples.
1.7.2 Examples of coordinate transformations
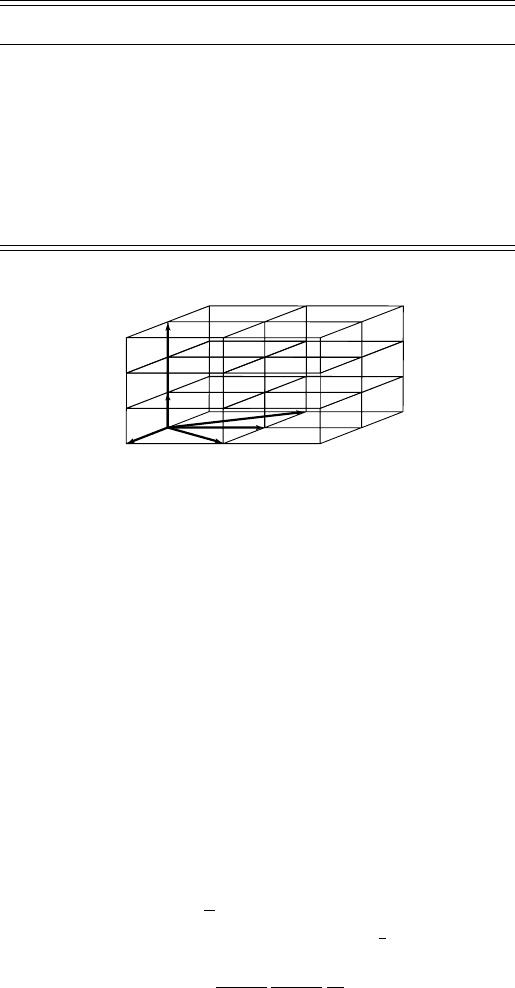
Example 1.15 Consider the two sets of basis vectors shown in Fig. 1.20; write down
the transformation matrix α
ij
. Show by explicit computation using the relations in
1.7 Coordinate transformations 51
Table 1.6. Overview of all transformation relations for
vectors and the metric tensor in direct and reciprocal
space. Pay close attention to the order of the indices!
Quantity Old to new New to old
Direct basis vectors a
i
= α
ij
a
j
a
i
= α
−1
ij
a
j
Direct metric tensor g
ij
= α
ik
α
jl
g
kl
g
ij
= α
−1
ik
α
−1
jl
g
kl
Direct space vectors p
i
= p
j
α
−1
ji
p
i
= p
j
α
ji
Reciprocal basis vectors a
∗
i
= a
∗
j
α
−1
ji
a
∗
i
= a
∗
j
α
ji
Reciprocal metric tensor g
∗
ij
= g
∗
kl
α
−1
ki
α
−1
lj
g
∗
ij
= g
∗
kl
α
ki
α
lj
Reciprocal space vectors k
∗
i
= α
ij
k
∗
j
k
∗
i
= α
−1
ij
k
∗
j
a
1
a
2
a
3
a'
1
a'
2
a'
3
Fig. 1.20. Unit cell drawing for Example 1.15.
Table 1.6 how the [uvw] direction and the (hkl) plane normal change to their new
values in the primed reference frame.
Answer: The transformation matrix α
ij
is easily derived from a visual inspection
of Fig. 1.20:
α
ij
=
110
−110
003
.
Direction indices transform according to the inverse of this matrix, or
$
u
v
w
%
=
[
uvw
]
α
−1
ji
;
=
1
2
[
uvw
]
1 −10
110
00
2
3
;
=
u + v
2
v − u
2
w
3
.

52 Basic crystallography
a
1
a
2
a
3
a'
1
a'
2
a'
3
Fig. 1.21. Unit cell drawing for Example 1.16.
Reciprocal lattice vectors transform according to the matrix α
ij
itself, or
h
k
l
= α
ij
h
k
l
=
110
−110
003
h
k
l
=
h + k
k − h
3l
.
Example 1.16 Consider the face-centered cubic lattice shown in Fig. 1.21; we
can define a primitive rhombohedral unit cell for this structure, as indicated by
the primed basis vectors. Determine the transformation matrix α
ij
, and express
the reciprocal basis vectors of the new reference frame in terms of those of the
old reference frame. Then compute the direct metric tensor for the primitive cell
using the transformation equations and show that the result is identical to the direct
computation of the metric tensor using the equations in Appendix A1.
Answer: The transformation matrix α
ij
is easily derived from a visual inspection
of Fig. 1.21:
α
ij
=
1
2
110
011
101
.
The reciprocal basis vectors transform according to the inverse of this matrix, or
a
∗
1
a
∗
2
a
∗
3
=
a
∗
1
a
∗
2
a
∗
3
α
−1
ji
;
=
a
∗
1
a
∗
2
a
∗
3
1 −11
11−1
−11 1
;
=
a
∗
1
+ a
∗
2
− a
∗
3
|−a
∗
1
+ a
∗
2
+ a
∗
3
|a
∗
1
− a
∗
2
+ a
∗
3
.
The direct metric tensor transforms according to g
ij
= α
ik
g
kl
α
jl
, or (note that
the matrix α
jl
must be transposed before multiplication since the summation index

1.7 Coordinate transformations 53
l must be the row index!)
g
ij
=
1
4
110
011
101
a
2
00
0 a
2
0
00a
2
101
110
011
;
=
a
2
4
110
011
101
101
110
011
;
=
a
2
4
211
121
112
.
The rhombohedral metric tensor is given by
g
ij
= b
2
1 cos α cos α
cos α 1 cos α
cos α cos α 1
,
where b and α are the lattice parameters of the primitive unit cell. From the draw-
ing one can easily show that b = a
√
2 and cos α =
1
2
, which leads to the same
expression for g
ij
.
1.7.3 Rhombohedral and hexagonal settings of the trigonal system
The derivation of the 14 Bravais lattices in Section 1.2.1 used the fact that all lattice
points must be equivalent; i.e. they must have the same environment. The centered
lattices can be obtained from the primitive lattices by placing additional sites at
positions given by the centering vectors A, B, C,orI. No other centering vectors
are allowed, except for the hexagonal crystal system. A number of space groups
describe symmetries that can be indexed in terms of a hexagonal reference frame
or a rhombohedral reference frame. This ambiguity has given rise to considerable
confusion in the literature. We will follow Burns and Glazer [BG90] (but with
a simplified notation) and derive the transformation relations between the two
descriptions.
Consider the hexagonal lattice shown in Fig. 1.6 on page 23. The lattice pa-
rameters are given by {a, a, c, 90, 90, 120} or {a, c} for short. When the standard
centering vectors are considered, no new lattices are obtained. However, when the
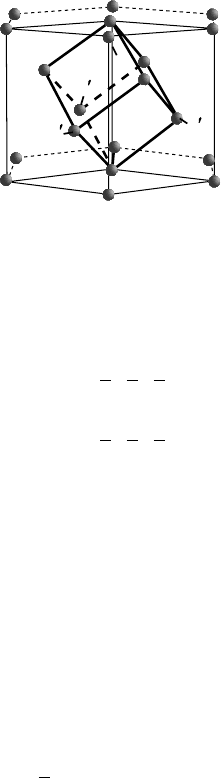
54 Basic crystallography
a
3
a
2
a
1
a
3
a
2
a
1
Fig. 1.22. Obverse setting of the rhombohedral lattice, with both hexagonal and rhombo-
hedral basis vectors indicated.
following centering vectors are used
R
1
=
2
3
,
1
3
,
1
3
;
R
2
=
1
3
,
2
3
,
2
3
,
a new lattice is obtained, since now all lattice points have identical surroundings. The
resulting lattice is shown in Fig. 1.22, with both hexagonal and rhombohedral basis
vectors indicated. The centering vectors above refer to the so-called obverse setting;
the reverse setting has the third components of the centering vectors exchanged.
The obverse setting is the preferred setting, according to the International Tables
for Crystallography [Hah96, page 79].
The transformation relation between the rhombohedral (primed) and hexagonal
(unprimed) lattices can be derived from Fig. 1.22:
a
1
a
2
a
3
=
1
3
211
−111
−1 −21
a
1
a
2
a
3
.
The inverse of this transformation matrix is given by
α
−1
=
1 −10
01−1
11 1
.
We can once again use the standard transformation relations in Table 1.6 to convert
quantities from one reference frame to the other.
The relations between the hexagonal lattice parameters {a, c} and {a
r
,α} of the
rhombohedral system can be derived as follows: the parameter a
r
is given by the

1.8 Converting vector components into Cartesian coordinates 55
length of the vector a
1
, or, using the hexagonal metric tensor,
a
2
r
=|a
1
|
2
=
1
18
$
211
%
2a
2
−a
2
0
−a
2
2a
2
0
002c
2
2
1
1
=
a
2
3
+
c
2
9
,
or
a
r
=
a
3
(
3 +
)
c
a
*
2
. (1.59)
The rhombohedral angle α follows from
a
1
· a
2
= a
2
r
cos α.
We have
a
1
· a
2
=
1
18
$
211
%
2a
2
−a
2
0
−a
2
2a
2
0
002c
2
−1
1
1
=
c
2
9
−
a
2
6
,
from which we find, after some simple rearrangements:
cos α = 1 −
9
2(c/a)
2
+ 6
. (1.60)
It is left as an exercise for the reader to invert these equations and to show that
a = a
r
√
2 − 2 cos α; (1.61)
c = a
r
√
3 + 6 cos α. (1.62)
1.8 Converting vector components into Cartesian coordinates
We have seen in previous sections that there is a distinct advantage to working
in crystal coordinates (i.e. in a non-Cartesian reference frame) in both direct and
reciprocal space. However, at the end of a simulation or calculation, the results
are almost invariably represented on a computer screen or on a piece of paper,
both of which are 2D media with essentially Cartesian reference frames. We must,
therefore, provide a way to transform direct and reciprocal crystal coordinates into
Cartesian coordinates. It is not difficult to carry out such a conversion for the
crystal systems of high symmetry (cubic, tetragonal, and orthorhombic) since their
coordinate axes are already at right angles to each other. However, for a monoclinic
or triclinic system the conversion to Cartesian coordinates is a bit more difficult and
it becomes important to have an algorithm that will do the conversion independent
of the crystal system. Such a conversion exists and is derived below. The derivation

56 Basic crystallography
a
1
a
2
a
3
a
3
e
1
e
2
e
3
*
Fig. 1.23. Definition of the Cartesian reference frame from the direct and reciprocal refer-
ence frames.
is somewhat tedious, but the resulting transformation is quite general and can be
used for both direct and reciprocal space quantities.
The transformation can be carried out by means of the so-called direct and
reciprocal structure matrices.
†
Let us assume a crystal reference frame a
i
, and the
corresponding reciprocal reference frame a
∗
j
. From these two reference frames we
can construct a Cartesian reference frame e
i
as follows: e
1
is the unit vector along
a
1
, e
3
is the unit vector along the reciprocal basis vector a
∗
3
(and is, therefore, by
construction normal to e
1
), and e
2
completes the right-handed Cartesian reference
frame (see Fig. 1.23):
e
1
=
a
1
|a
1
|
;
e
2
= e
3
× e
1
;
e
3
=
a
∗
3
|a
∗
3
|
=
a
1
× a
2
|a
∗
3
|
.
(1.63)
We will refer to this reference frame as the standard Cartesian frame. Now consider
a vector r with components r
i
with respect to the basis vectors a
i
. The components
of r in the Cartesian reference frame are given by x
j
,or
r = r
i
a
i
= x
j
e
j
.
The components r
i
and x
j
are related to one another by a linear coordinate trans-
formation represented by the matrix a
ij
:
x
i
= a
ij
r
j
.
The elements of the transformation matrix can be determined as follows:
equations (1.63) are rewritten in terms of the direct and reciprocal metric
†
This section follows the same conventions as those used in the EMS software package [Sta87].

1.8 Converting vector components into Cartesian coordinates 57
tensors as
e
1
=
a
1
√
g
11
;
e
2
=
a
∗
3
× a
1
g
11
g
∗
33
;
e
3
=
a
∗
3
g
∗
33
=
g
∗
3m
a
m
g
∗
33
.
From the definition of a
∗
3
we derive
a
∗
3
× a
1
= (a
1
× a
2
) × a
1
=−a
1
× (a
1
× a
2
).
The triple vector product can be simplified using the vector identity
u × (v × w) = (u · w)v − (u · v)w,
which leads to
a
∗
3
× a
1
= g
11
a
2
− g
12
a
1
,
and finally
e
2
=
g
11
a
2
− g
12
a
1
g
11
g
∗
33
.
The vector r can now be written as follows:
r = x
j
e
j
=
+
x
1
√
g
11
−
g
21
x
2
g
11
g
∗
33
+
g
∗
31
x
3
g
∗
33
,
a
1
+
+
g
11
x
2
g
11
g
∗
33
+
g
∗
32
x
3
g
∗
33
,
a
2
+
g
∗
33
x
3
g
∗
33
a
3
.
Using the fact that the direct and reciprocal metric tensors are each other’s inverse,
we can explicitly write the matrix a
ij
as
a
ij
=
√
g
11
g
21
√
g
11
g
31
√
g
11
0
g
∗
33
g
11
−
g
∗
32
√
g
∗
33
g
11
00
1
√
g
∗
33
;
=
abcos γ c cos β
0 b sin γ −
cF(β,γ,α)
sin γ
00
ab sin γ
, (1.64)
