Graef M. Introduction to conventional transmission electron microscopy

Подождите немного. Документ загружается.

78 Basic crystallography

(e) Compute the angle between the (001) and (111) plane normals.

(f) Compute the direct space components of the plane normal g

113

(g) Write down the explicit expressions for the reciprocal basis vectors. From these

expressions, derive the reciprocal lattice parameters.

(h) Compute the cross product between the direction vectors [100] and [01

1], and

express it in both the direct and reciprocal reference frames.

(i) Compute the Cartesian components of the point (1, −1, 1) (standard Cartesian

reference frame).

(j) Compute the Cartesian coordinates of the reciprocal lattice point (111).

1.2 Consider a monoclinic unit cell, with lattice parameters {2, 1, 1, 90, 45, 90}. Use a

unit distance of 4 cm (i.e. a lattice parameter of 1 should correspond to 4 cm on your

drawing). The b axis points down into the plane of the drawing, normal to both a

and c which lie in the plane of the drawing.

(a) Draw the

basis vectors and the following planes (in different colors or

linestyles):

(101), (201), (10

1), and (102).

(b) Draw the reciprocal basis vectors a

∗

and c

∗

to scale and in the proper orientation

with respect to the basis vectors a

ven above, based on the reciprocal basis

vectors. All g-vectors should start in the origin and use the same linestyle/color

as the corresponding planes.

(d) Measure the d-spacings on the drawing (in units of 4 cm), and calculate |g| for

each plane; verify that d = 1/|g| (to within the accuracy of your drawing).

1.3 Show that for a cubic crystal system, the direction [uvw] is always parallel to the

plane normal on the plane with Miller indices (uvw).

1.4 Use equation (1.28) to derive relation (1.21).

1.5 Show that the inverse of the Seitz operator (D|t) is given by (D

−1

|−D

−1

t).

1.6 Consider the six-fold axis

located at the point (

, 0) and parallel to the e

direction. What is the corresponding matrix W? (Hint: Decompose the operator into

two translations and a rotation, in the proper order.)

1.7 Write down all the 3 × 3 symmetry matrices for the elements of the point group

6m2

with respect to the hexagonal basis vectors.

1.8 Consider the body-centered cubic Bravais lattice. Deﬁne a primitive unit cell for this

structure and determine the transformation equations for directions and planes with

respect to the conventional cubic basis vectors.

1.9 Derive equations (1.61) and (1.62) on page 55.

1.10 Work out the transformation matrices E

, E



, and α

for the following orientation

relation in a tetragonal crystal with lattice parameters {a, c}:

(011)

 (011)

,[0

11]

 [01

Basic quantum mechanics, Bragg’s Law, and other tools

2.1 Introduction

One of the principal goals of transmission electron microscopy (TEM) is to ob-

serve and determine the crystallographic nature of a variety of features in materials,

from the actual crystal structure to the detailed atomic conﬁgurations and chem-

istry around defects. In the previous chapter, we introduced the mathematical tools

needed to describe crystal structures and to perform geometric computations in an

arbitrary Bravais lattice. In the present chapter, we introduce another set of tools

that are used to describe the interactions between electrons and the specimen.

Since observation of a phenomenon or an object always implies an interaction

between the observer and that object, it is important that such observations be car-

ried out under the proper conditions. For instance, to determine the color of an

object, we would typically illuminate the object with white light, and analyze the

frequencies of the reﬂected light, while to determine the ﬂuorescent properties of

that same object we would illuminate it with ultraviolet light, and so on. Estab-

lishing the proper observation conditions is thus crucial to the subsequent success

of the observation. Since the object modiﬁes the incident illumination, we can ex-

tract valuable information about the object by carefully analyzing this modiﬁed

signal.

To determine the crystallographic characteristics of a material, we illuminate it

with electrons. It is thus intuitively clear that the TEM must consist of three major

stages:

(i) the illumination stage, which creates a beam of electrons in a well-deﬁned reference

state;

(ii) the interaction stage, where the sample modiﬁes the reference state of the electron

beam; and

(iii) the observation stage, where the modiﬁed electron beam is converted into a signal that

can be detected by the human eye.

80 Basic quantum mechanics

In the early part of the twentieth century, the importance of the observer as part

of an experiment was recognized, and it became clear that a system of interacting

particles cannot be observed without actually modifying that system by the very act

of observing it. In classical mechanics, which deals with the motion of macroscopic

objects, the observer is rarely an important part of the equation, but in the atomistic

world things are quite different. The development of quantum mechanics (QM) in

the ﬁrst quarter of the twentieth century led to the incorporation of the observer into

the physical system, and, more importantly, led to a new understanding of what a

physical observable is. Since the electron microscope uses atomistic particles to

probe the internal structure of materials, it is clear that the theory describing image

formation in TEM must by necessity be of a quantum mechanical nature.

In addition to behaving by the rules of quantum mechanics, the electrons in a

typical TEM move at a velocity that is a substantial fraction of the velocity of

light. Motion at such high velocities must follow the rules of the special theory

of relativity. We thus conclude that an observation in a TEM is essentially an

experiment in relativistic quantum mechanics. Fortunately it is not necessary to

have an advanced physics degree to understand how a TEM works, or to interpret

the images obtained in various observation modes.

In this chapter, we shall discuss basic quantum mechanics and the special theory

of relativity at the level required for the later chapters in this book. We will see that,

once the proper starting equation (or governing equation) is obtained, we need no

longer explicitly worry about the relativistic nature of a TEM observation. Then we

introduce Bragg’s Law in direct and reciprocal space and, starting from quantum

mechanics, we deﬁne the Fourier transform, which essentially transforms quanti-

ties between the two spaces. We derive expressions for diffraction from inﬁnite and

ﬁnite lattices, and conclude the chapter with a description of a numerical proce-

dure to compute the electrostatic lattice potential. Along the way, we introduce an

expression for the wavelength of a relativistic electron.

2.2 Basic quantum mechanics

Classical physics describes how a macroscopic object behaves when it is subjected

to external forces. When the properties of the object are known (mass, mass dis-

tribution, size, shape, etc.), together with the forces acting on that object, then the

equations of classical physics allow us to compute how this object will behave as

a function of time. We can calculate the position and the orientation of the object

at any given moment in time. More importantly, we can measure the position, mo-

mentum, angular momentum, and energy of the object simultaneously (with proper

measuring tools). Classical physics is therefore deterministic, since knowledge of

the observables at one point in time allows integration of the equations of motion

2.2 Basic quantum mechanics 81

to any later (or earlier) moment in time. The mathematical framework of classi-

cal physics can be formulated at various levels, using Lagrangian or Hamiltonian

equations of motion, and it can be shown that all of classical physics can be derived

from the principle of least action [Gol78].

With the discovery of quantum mechanics in the early part of the twentieth

century, it became clear that the laws of classical physics are no longer valid in

the atomistic realm. The fundamental difference between classical physics and

quantum mechanics is that a physical observable cannot always be measured with

absolute certainty and, instead, one can only compute probabilities that a particle

will be at a certain location, with a certain momentum or angular momentum,

etc. In quantum mechanics, physical observables no longer satisfy deterministic

equations, and, therefore, the classical concept of a particle trajectory is no longer

valid. The probabilities or expectation values of physical observables are computed

from a function which is the solution to the Schr

odinger equation. This function is

known as the wave function of the system.

2.2.1 Scalar product between functions

The basis of the mathematical formalism of quantum mechanics lies in the propo-

sition that the state of a system of N particles can be described by a deﬁnite, in

general complex-valued, function  of the particle coordinates r

(i = 1,...,N ).

†

The square of the modulus of this function, ||

, describes the probability distribu-

tion of the value of the coordinates. The function  is called the wave function of

the system, and it expresses the probability amplitude. All physical observables are

expressions bilinear in  and 

∗

, where the asterisk denotes complex conjugation.

If an observable is represented by the symbol f , then the expectation value of f is

given by

 f =

...



∗

(r) f (r)dr,

where the integration extends over all of space. The primary goal of quantum

mechanics is thus to compute the wave function  for a given system of particles.

Once the wave function is known, the expectation values of all physical observables

can be computed using expressions of the type above. Note that a wave function 

need only be determined to within a constant phase factor of the form e

iα

, with α a

real number, since the phase factor cancels out when substituted in the expression

for the expectation value of an observable.

†

In this section we closely follow Chapter 2 of the book Quantum Mechanics by L.D. Landau and E.M. Lifschitz

[LL74].

82 Basic quantum mechanics

Since many computations in QM involve integrals of the above type, it is conve-

nient to introduce a shorthand notation, ﬁrst suggested by Dirac [Dir47, pp. 14–22].

For a given observable f , and two wave functions  and , we deﬁne the following

symbol:

| f |≡

...



∗

f . (2.1)

The symbol ||is known as the bra-ket. Note that there is no mention of the

coordinate variable at all; the deﬁnition (2.1) does not depend on the particular

representation or basis in which the wave functions are expressed.

The bra-ket notation is rather similar to that of the dot product between two

vectors. The symbol | f | means: take the function |, operate on it with the

operator or function f , and project the result onto the function |. In the absence

of an operator f , we can deﬁne the scalar product of two functions  and  as

(taking f = 1):

|=

...



∗

. (2.2)

If |=0, then we say that the functions  and  are orthogonal functions,

in the same way that two vectors p and q are orthogonal when p · q = 0. If, in

addition, |=1 and |=1, then the functions  and  are normalized

orthogonal or orthonormal functions.

2.2.2 Operators and physical observables

In QM, every physical quantity is described by an operator

f . An operator can be

represented by a simple multiplication by a number, or a combination of partial

derivatives, or an integral, etc. The allowed values of this physical quantity are

the eigenvalues of the operator. The spectrum of eigenvalues can be discrete, e.g.

the energy levels of the bound states of the hydrogen atom, or continuous, e.g. the

momentum of a free particle. To compute the value of a certain physical observable,

we must determine which wave functions are eigenfunctions of the corresponding

operator; i.e. we must solve the equations

f |

= f

|

, with n = 1, 2,.... (2.3)

This results in a (possibly inﬁnite) set of eigenfunctions |

 with (possibly com-

plex) eigenvalues f

. The real physical state of the system is then described by a

linear superposition of all these eigenstates, i.e.

|=



|

, (2.4)

2.2 Basic quantum mechanics 83

where c

are complex numbers. The expectation value of the operator

f for a system

in the state | is then given by



f =|

f |=





∗









|





. (2.5)

Using equation (2.3) this can be rewritten as



f =



∗



f |

=



m,n

∗



|

. (2.6)

If the set of eigenfunctions 

is complete [Ode79] and orthonormal, then the ﬁnal

bra-ket can be rewritten as



|

=δ

, (2.7)

from which



f =



m,n

∗



. (2.8)

The expectation value of the physical observable f is hence equal to the sum of

the squares of the moduli of the coefﬁcients c

, weighted by the eigenvalues of the

operator

f . This is a very general result, valid for all operators.

An example may clarify the use of these equations. In classical mechanics, the

kinetic energy T of a free particle is described by

T =

, (2.9)

with m

the rest mass of the particle. The momentum of classical mechanics is

translated into a momentum operator

p =−i h

∇, where h is Planck’s constant h =

6.626 075 × 10

−34

J s, divided by 2π, and ∇ is the gradient differential operator.

†

The eigenvalues p and eigenfunctions | of this operator are determined from the

equation:

p|=−i h

∇|=p|, (2.10)

or, in the coordinate representation:

−i h

∇(r) = p(r).

This equation has solutions of the form

(r) = Ce

p·r

. (2.11)

†

The differential form of the momentum operator is a consequence of the invariance of a closed system of particles

with respect to inﬁnitesimal translations. For a derivation of the operator we refer to Section 12 in [LL74], or

Section 25 in [Dir47].

84 Basic quantum mechanics

The constant C follows from the normalization condition |=1 and we leave

it as an exercise for the reader to show that C = h

−3/2

The allowed values of the momentum eigenvalue p form a continuous spectrum.

The kinetic energy operator becomes

T =

=−

∇

. (2.12)

The eigenvalue equation for the kinetic energy operator has the same eigenfunctions

as the momentum operator (for a free particle), but with different eigenvalues:

−

∇

p·r

. (2.13)

The average kinetic energy of a free particle can hence be computed as follows:



T =|

T |=

|=

, (2.14)

and we ﬁnd the classical expression for the kinetic energy.

2.2.3 The Schr¨odinger equation

In classical mechanics, the equations of motion can be derived from either the

Lagrangian or the Hamiltonian functions, depending on the approach [Gol78]. The

Hamiltonian of a classical system of interacting particles can be written as

H = T + V, (2.15)

where V is the potential energy of the particles. Using variational principles, one can

derive the Hamiltonian equations of motion, or, equivalently, the Euler–Lagrange

equations of motion, from which all of classical mechanics can be derived, including

Newton’s equations.

In quantum mechanics, the Hamiltonian function is converted into a Hamiltonian

operator:

H =

T +

V . (2.16)

We can again formulate an eigenvalue equation for these operators:

H|=(

T +

V )|=E

|, (2.17)

where E

is the total energy of the system. The Hamiltonian operator describes the

time evolution of the system and can be rewritten in differential form as

H|=i h

∂

∂t

|. (2.18)

2.2 Basic quantum mechanics 85

This expression follows from the fact that the time derivative of the wave function

at any given instant is determined by the value of the function | itself at that

instant, which leads to a linear (ﬁrst-order) relation [LL74]. Combining the above

equations results in the time-dependent Schr

odinger equation:

i h

∂

∂t

|=(

T +

V )|=E

|. (2.19)

For a free particle,

V = 0, the solution to this equation is given by (r, t) =

−

t−p·r)

. This solution represents a plane wave with energy E

= p

/2m

and momentum p. The wave has a frequency ν = E/h = 2πω.

The stationary (or time-independent) Schr

odinger equation takes the form:

|+[E

−

V ]|=0, (2.20)

where we have replaced the kinetic energy operator by its differential form. These

equations were obtained by Schr¨odinger in 1926 [Sch26] and from them most of

QM can be derived. We refer to standard QM textbooks for detailed discussions of

the Schr¨odinger equation and other aspects of quantum mechanics, such as angular

momentum and the Heisenberg uncertainty principle (e.g. [Hei25]).

The examples above show that the wave function is the central object in quantum

mechanics. When the wave function is known, the expectation values of all physical

observables can be calculated. The momentum eigenfunctions are very important

for electron scattering, since a scattering process generally involves momentum

transfer. As we will see in later chapters, all of electron diffraction theory can be

expressed with the tools introduced in this and the following sections.

2.2.4 The de Broglie relation

In a seven-page doctoral thesis, Louis de Broglie [de 23] postulated in 1924 that

all particles have some wave-like properties (wave–particle duality); he associated

a wavelength λ with the momentum, p, of a particle:

λ =

. (2.21)

Deﬁning the wave number k as k = 1/λ, this relation can be rewritten as p = hk,

or, in vector form, p = hk. This establishes a linear relation between momentum

space and reciprocal space, since |k| has the dimensions of a reciprocal length. As

a consequence of the de Broglie relation, we ﬁnd that reciprocal space is identical

to momentum space, apart from a scaling factor (Planck’s constant).

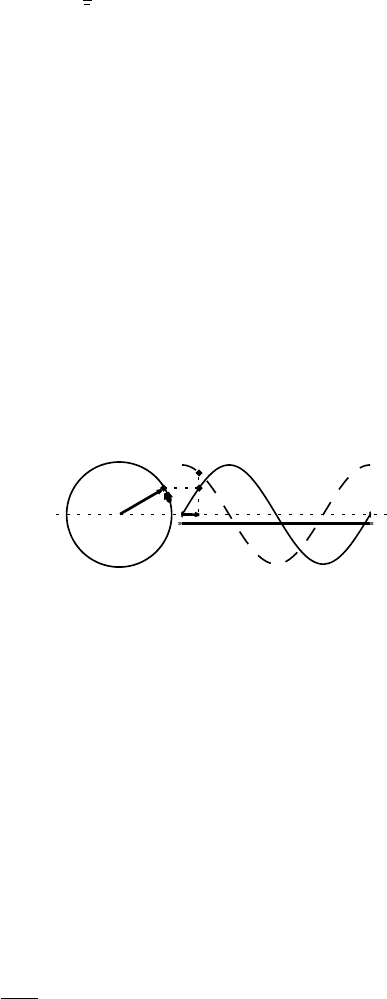
86 Basic quantum mechanics

We can now consider the wave function of a particle in coordinate space and

write it as a linear combination of the momentum eigenfunctions:

(r) = C



·r

;



2πik·r

. (2.22)

The constant C has been absorbed in the coefﬁcients c

. If the eigenspectrum of

the momentum operator is continuous, then the summation must be replaced by an

integral. Expansion of a wave function in terms of plane waves is very important

for the description of diffraction phenomena, as we will see in later chapters and in

Section 2.5.

Since plane waves form the basis for much of electron diffraction theory, it is

perhaps useful to take a closer look at the properties of a plane wave. By deﬁnition,

a plane wave is an eigenfunction of the momentum operator

p. It is easy to see

why such a function is called a plane wave: if the argument of the exponential is

constant, i.e. k · r = d, then the value of the wave function is constant:

|=e

2πid

= cos(2πd) + i sin(2π d).

It is not difﬁcult to see that the geometric locus of all the vectors r satisfying the

equation k · r = d is a plane perpendicular to the vector k. The wave function

takes on all values on the complex circle with unit radius when d goes to d + 1

or, equivalently, when the wave advances one wavelength λ. The sketch above

shows the real (R) and imaginary (I) components of one wavelength of the plane

wave.

2.2.5 The electron wavelength (non-relativistic)

Assume that an electron is accelerated by an electrostatic potential drop E. The

potential energy of the electron is then equal to eE and when the electron leaves

the ﬁeld region, it will have acquired a kinetic energy given by

T =

= eE, (2.23)

2.2 Basic quantum mechanics 87

Table 2.1. Non-relativistic electron

wavelengths (in pm) for selected

acceleration voltages E (in volts). The

relativistic values are given in the last

column (using equation 2.33).

E (volt) λ

(pm) λ (pm)

100 122.64 122.63

500 54.84 54.83

1 000 38.78 38.76

5 000 17.34 17.30

10 000 12.26 12.20

20 000 8.67 8.59

where m

is the rest mass of the electron. As we have seen above, the de Broglie

equation relates the momentum p to the (non-relativistic) electron wavelength

and thus

eE =

which can be rewritten as

√

1226.39

√

. (2.24)

When the voltage is expressed in volts, the wavelength is given in picometers.

This equation is valid for low acceleration potentials E (up to about 10 000 V),

and a selection of wavelengths is shown in Table 2.1. For comparison the table

also shows the relativistic values, computed from equation (2.33) on page 92. It

can be seen that the corrections are small, which means that for the acceleration

voltages typically used in a scanning electron microscope (SEM) it is a reasonable

approximation to use the non-relativistic expression (2.24).

2.2.6 Wave interference phenomena

Interference between particle waves is a purely quantum mechanical effect, and it

lies at the heart of transmission electron microscopy. In classical mechanics, the