Gubbins D., Herrero-Bervera E. Encyclopedia of Geomagnetism and Paleomagnetism

Подождите немного. Документ загружается.

of rolling along the surface of the depositional plane in the direction

of current flow.

In general, AMS studies in deep-sea sediments call attention to the

need for a better unders tanding of the relationship between the shape

and orientation of AMS ellipsoids and current flow, such that transport

mechanisms and sedimentation processes in deep-sea sediments (for

example, turbidites, contourites, and channel deposits), can be identifi ed

using AMS data. Recent studies ind icate bioturbation is a widespread

and continuous process, which disturbs deep-sea sediments. Flood et al.

(1985) evaluated the effect of bioturbation on AMS fabrics in deep-sea

sediments and found characteristic alteration from weakly oblate, to sec-

ondary prolate fabrics in the uppermost centimeters of sediment. More

study is need ed to assess the degree to which deep-sea sediment fabrics

are generally affected by bioturbation.

Grain orientations determined by microscopic measurement and

AMS measurements in experimentally produced fluvial and wind-

deposited (eolian) sands were compared by Taira (1989). The study

demonstrates the usefulness of AMS fabric in identification of sedi-

ment depositional processes. From analysis of experimentally pro-

duced fabrics, five distinct modes of deposition (gravity, flat bed and

sloping bed, current, grain collision, and viscous flow) were distin-

guished, each with characteristic fabric parameters. In general, the

maximum susceptibility was found to be oriented parallel to the cur-

rent (shear stress) direction, whereas the minimum susceptibility was

found to be oriented near normal, but with a distinct angle to the plane

of shear stress (the imbrication angle). The five depositional types

recreated in experimentally deposited sediments were found to fall into

distinct groupings when two AMS measurement parameters are plotted

against one another. The magnetic foliation/lineation (q) was plotted

against the angle of imbrication of the minimum susceptibility axis

) relative to the bedding plane (b).

Many useful measurement parameters, such as q and b, which

describe the magnitude, shape, or orientation of the AMS ellipsoid,

have been defined. See Magnetic susceptibility, anisotropy (q.v.) for

a complete treatment.

Strain alteration of sedim entary fabrics

Many studies have successfully correlated the orientation of the princi-

pal axes of the AMS ellipsoid with mesoscopic rock fabrics. More

recent efforts have concentrated on correlating the AMS ellipsoid

and the finite strain ellipsoid (for a review, see Tarling and Hrouda,

1993). While these studies have, in the main, found that the finite

strain and susceptibility ellipsoids are coaxial in orientation, the com-

pelling goal of such research is to quantitatively relate the AMS fabric

of a strained rock with its measured strain (using passive markers for

example). Such studies have been complicated by variations in mag-

netic mineralogy, for example, and attempts to correlate the magni-

tudes of the finite strain ellipsoid and the AMS ellipsoid continue to

be a challenge (for a review, see Borradaile, 1988).

Some features of strain-induced modification to sedimentary AMS

fabrics are well documented. A basic idea, common to interpretation

of AMS in strain studies, is the concept that as primary principal axes

are deformed, they will be deflected away from their original direction.

As the intensity of strain increases, magnetic foliations tend to tilt

away from the bedding plane, forming a “girdle” of poles parallel to

the direction of shortening. Thus, fabrics can often show girdling of

principal directions as the axes progressively reorient from originally

clustered principal directions. This has allowed some workers to use

AMS to reverse the strain from a rock in order to correct the remanent

magnetization directions, resulting in improved clustering of the rema-

nence directions (for a review, see Cogne and Perroud, 1987).

Tectonic lineations

Secondary magnetic lineations acquired through transitional tectonic

strains are reported (often termed a “pencil structure,” Graham, 1978;

Kligfield et al., 1981). A pencil structure can be thought of as ana-

logous to the intersection fabric between cleavage and bedding

commonly used in structural analysis. In a true pencil structure, indivi-

dual grains are mechanically and progressively rotated toward a direc-

tion perpendicular to the direction of principal stress, producing a

lineation normal to the shortening direction. While fabrics of this type

are often reported, clearly, magnetic susceptibility axes and grain-

shape do not correspond in all of these fabrics. For instance, many

AMS fabrics found in weakly strained sediments in young compres-

sional mountain belts show K

in the bedding plane and perpendicular

to the direction of tectonic transport, much like a pencil structure.

These AMS maximum axes are often well-grouped perpendicular to

the direction of principal stress, and are usually interpreted as having

a tectonic origin. Such well-grouped magnetic lineations, however,

are often reported in visually undeformed sediments, in which an ana-

logous rigid deformation of the rock fabric seems very unlikely with

such weak deformation.

Such fabrics can be explained by observing that, when principal axes

have nearly equal magnetic susceptibilities, exchanging of axes can be

instantaneous with very small increments of strain. A reorientation of



in the maximum susceptibility axis in very weakly strained rocks,

with no girdling of principal axes, is the result. Consider an assemblage

of magnetic grains with an initial sedimentary fabric, having a foliation

in the bedding plane and K

oriented in a downstream direction (for

example, perpendicular to a compressional mountain range). Any short-

ening parallel to the bedding plane will have the effect of tilting the

grains away from the bedding plane, thereby weakening the K

of the

bulk fabric, but leaving K

unchanged. At some point, the susceptibility

of K

and K

will become equal, and with the next increment of strain

their orientations will abruptly exchange. In this way, a “pencil struc-

ture” might seem to develop with very weak strains as the susceptibility

of initially well-clustered K

axes are diluted by small changes in the

grain orientations. This is most likely to occur with K

and K

very nearly

equal in magnitude. Exchanging susceptibility axes, as in this example,

can result in the “inverted fabrics” reported by some studies; grains

will not physically reorient with very low strain, but the bulk AMS

ellipsoid may.

An evolution of syndeformational magnetic fabrics was suggested

in a study of sediments from a Neogene accretionary complex by

Kanamatsu et al. (1996). In that study, sedimentary AMS fabrics were

found to follow a path of decreasing shape parameter (T ) and decreas-

ing degree of corrected anisotropy (P

) with the evolution from sedi-

mentary through transitional to “tectonic” fabrics. That is, AMS

ellipsoids were found to vary during weak progressive strain from

oblate to prolate in shape, while anisotropy decreased (the shape para-

meter (T ) and corrected anisotropy (P

) have been adopted as standard

parameters to evaluate AMS ellipsoids, and are discussed in Jelinek,

1981).

Strain-induced changes in mineral composition

Since AMS is determined from the combined susceptibility of all para-

magnetic, diamagnetic, and ferromagnetic minerals in a sample,

increased intensities of strain produces an important caveat for AMS

studies. The growth of minerals through dissolution and recrystalliza-

tion processes accompanying increased strain hampers interpretation

of AMS ellipsoids. Housen and van der Pluijm (1990) demonstrated

control of paramagnetic chlorite on AMS fabrics during development

of slaty cleavage. Since magnetic anisotropy increases with increasing

degree of crystallographic preferred orientation, the AMS ellipsoid

can be determined by the crystallographic principal axes. Such studies

point to the need for a thorough understanding of the paramagnetic

and diamagnetic matrix as well as ferromagnetic constituents, espe-

cially under conditions of progressive strain. Fortunately, rock magnetic

methods are providing increasingly sophisticated means to separate fer-

romagnetic and paramagnetic contributions to the susceptibility tensor.

476 MAGNETIC ANISOTROPY, SEDIMENTARY ROCKS AND STRAIN ALTERATION

For example, the anisotropy of anhysteretic remanent magnetization

(AARM) (see Magnetization, anhysteretic remanent (ARM), q.v.)isa

method unaffected by paramagnetic constituents. In many cases, a rea-

sonable approximation of single mineral anisotropies can increasingly

be obtained. These methods will continue to provide exciting opportu-

nities to advance the state of research relating magnetic fabrics and rock

fabrics.

Peter D. Weiler

Bibliography

Borradaile, G.J., 1988. Magnetic susceptibility, petrofabrics and strain.

Tectonophysics, 156:1–20.

Cogne, J.P., and Perroud, H., 1987. Unstraining paleomagnetic vec-

tors: the current state of debate. EOS Transactions of American

Geophysical Union, 68(34): 705–712.

Ellwood, B.B., 1980. Induced and remanent properties of marine sedi-

ments as indicators in depositional processes. Marine Geology, 38:

233–244.

Flood, R.D., Kent, D.V., Shor, A.N., and Hall, F.R., 1985. The mag-

netic fabric of surficial deep-sea sediments in the HEBBLE area

(Nova Scotian Continental Rise). Marine Geology, 66: 149–167.

Graham, R.H., 1978. Quantitative deformation studies in the Permian

rocks of the Alpes-Maritimes. Memoire de Bureau de Recherches

Geologiques et Minieres, 91: 219–238.

Housen, B.A., and van der Pluijm, B.A., 1990. Chlorite control of cor-

relations between strain and anisotropy of magnetic susceptibility.

Physics of the Earth and Planetary Interiors, 61: 315–323.

Jelinek, V., 1981. Characterization of the magnetic fabric of rocks.

Tectonophysics, 79:63–67.

Kanamatsu, T., Herrero-Bervera, E., Taira, A., Ashi, J., and Furomoto,

A.S., 1996. Magnetic fabric development in the Tertiary accretion-

ary complex in the Boso and Miura Peninsulas of Central Japan.

Geophysical Research Letters, 23: 471–474.

Kligfield, R., Owens, W.H., and Lowrie, W., 1981. Magnetic suscept-

ibility anisotropy, strain, and progressive deformation in Permian

sediments from the Maritime Alps (France). Earth and Planetary

Science Letters, 55: 181–189.

Taira, A., 1989. Magnetic fabrics and depositional processes. In Taira,

A., and Masuda, F. (eds.), Sedimentary Facies in the Active Plate

Margins. Tokyo: Terra Science, pp. 43–77.

Tarling, D.H., and Hrouda, F., 1993. The Magnetic Anisotropy of

Rocks. New York: Chapman & Hall.

Cross-references

Magnetic Susceptibility, Anisotropy

Magnetization, Anhysteretic Remanent (ARM)

MAGNETIC ANOMALIES FOR GEOLOGY

AND RESOURCES

Magnetic anomalies and geological mapping

Knowledge of the geology of a region is the scientific basis for

resource exploration (petroleum, solid minerals, groundwater) the

world over. Among the variety of rock types to be found in the Earth’s

crust, many exhibit magnetic properties, whether a magnetization

induced by the present-day geomagnetic field, or a remanent magneti-

zation acquired at some time in the geological past, or a combination

of both. Mapping the patterns of magnetic anomalies attributable to

rock magnetism has proved to be a very effective way of reconnoiter-

ing large areas of geology at low cost per unit area. The fact that most

sedimentary rocks and surface-cover formations (including water)

are effectively nonmagnetic means that the observed anomalies are

attributable to the underlying igneous and metamorphic rocks

(the so-called “magnetic basement”), even where they are concealed

from direct observation at the surface. Anomalies arising from the

magnetic basement are only diminished in amplitude and extended in

wavelength through the extra vertical distance between source and

magnetometer imposed by the nonmagnetic sediment layers. Thus

aeromagnetic surveys (q.v.) are able to indicate the distribution of bed-

rock lithologies and structures virtually everywhere. Interpretation of

magnetic anomaly patterns can then lead to maps of (hidden) geology

that give direction to the exploration process (Figure M1/Plate 7b). In

igneous and metamorphic (“hard rock”) terranes, outlines of local

areas promising for the occurrence of ore bodies can be delineated

for closer follow-up studies. In the case of petroleum exploration,

interpretation of the structure of the underlying basement can help

understanding of basin development and help locate areas for (costly)

seismic studies and drilling. Similar economies in the exploration pro-

cess can be made through exploitation of aeromagnetic surveys in the

systematic mapping of potential groundwater resources, of particular

importance in the arid and semiarid areas of the world.

Mineral exploration

The amplitude, shape, and internal texture of magnetic anomalies may

be used to indicate the likelihood of finding of certain ore types. Initi-

ally, aeromagnetic measurements were used in direct prospecting for

magnetic iron ores and in the indirect detection of certain classes of

magmatic-hosted Ni-deposits, kimberlite pipes for diamonds, and so

forth. Hydrothermally altered areas in magnetic environments are often

detectable as low magnetic zones and may be prospective for Au and

Pb. The largest concentrated source of magnetic anomaly in terms of

magnetic moment is the Kursk low-grade magnetic iron-quartzite ore

formation in Ukraine that can be measured even at satellite altitudes.

Most of the major satellite anomalies are, however, attributable to entire

provinces of relatively magnetic rocks, such as Northern Fennoscandia,

of which the Kiruna magmatic iron ore is but a tiny part.

Most ore deposits within the crystalline basement are, either in

themselves or through their host rocks, accompanied by magnetic

Figure M1/Plate 7b (a) Magnetic anomaly patterns over part of

Western Australia recorded in various aeromagnetic surveys.

(b) Geological interpretation of the data shown in (a). (Courtesy

of Geoscience Australia and the Geological Survey of Western

Australia).

MAGNETIC ANOMALIES FOR GEOLOGY AND RESOURCES 477

anomalies. These anomalies are often used further in the closer evalua-

tion of the extent and geometry of a deposit and in assessing the

mineral potential of other comparable geological formations. At

the reconnaissance stage of mineral assessment, area selection and pro-

specting—particularly of soil-covered areas of crystalline basement—

geological mapping can be driven in large part by interpretation of

detailed aeromagnetic anomaly maps. These provide, in a cost-effective

and environmentally friendly way, a reliable picture of the underlying

subsurface, including the location and extent of geological units and

their lithology, structure, and deformation.

Continental and oceanic anomaly mapping

Given that most countries have a national program of mineral resource

management, the foundation of which is the geological mapping

program at an appropriate scale (say 1:1000000), ambitious national

programs of aeromagnetic anomaly mapping have been instigated gen-

erally to supplement and accelerate geological mapping (for example

Canada, Australia, former Soviet Union, the Nordic countries).

National aeromagnetic anomaly maps, together with gravity anomaly

maps, have therefore become preeminent in the geophysical support

of geological reconnaissance. Given that gamma-ray spectrometer

surveys are now usually flown simultaneously with aeromagnetic sur-

veys at little additional cost, they form a third common type of geo-

physical support for geological mapping.

Over 70% of the Earth is covered by oceans. The geology here is

totally obscured, even over the continental shelves. Until the advent

of systematic ocean exploration in the second half of the 20th century,

little was known of the geological evolution of the deep oceans. The pat-

terns of magnetic anomaly stripes discovered, paralleling the mid-ocean

ridges (Figure M2/Plate 9e from Verhoef et al., 1996), became one of

the leading lines of evidence in support of continental drift and, even-

tually, global tectonics (see Vine-Matthews-Morley hypothesis). This

revelation must count as one of the most profound advances in our

understanding of the Earth’s history and its mode of development.

Being of igneous origin, the rocks of the oceanic crust solidify and

cool at the mid-ocean ridge while inheriting a magnetic field direction

from the erstwhile geomagnetic field. Repeated reversals of that field

are recorded symmetrically either side of the ocean-spreading axis as

new crust is relentlessly added, a few centimeters per year, at the axis

itself. While people’s interest in mineral resources of the deep ocean is

still limited, understanding the previous locations of the continents,

particularly during the past 200 Ma for which ocean floor can still

be found, is central to our understanding of geological processes in

this period. The sedimentary rocks laid down on the passive continen-

tal margins now separated by “new” oceans host a great deal of the

world’s hydrocarbon reserves.

Ocean crust is eventually recycled into the Earth’s mantle via sub-

duction zones with the result that ocean crust in situ older than about

200 Ma is no longer to be found. Evidence of the earlier 95% of geo-

logical history is therefore confined to the continents. Here a great deal

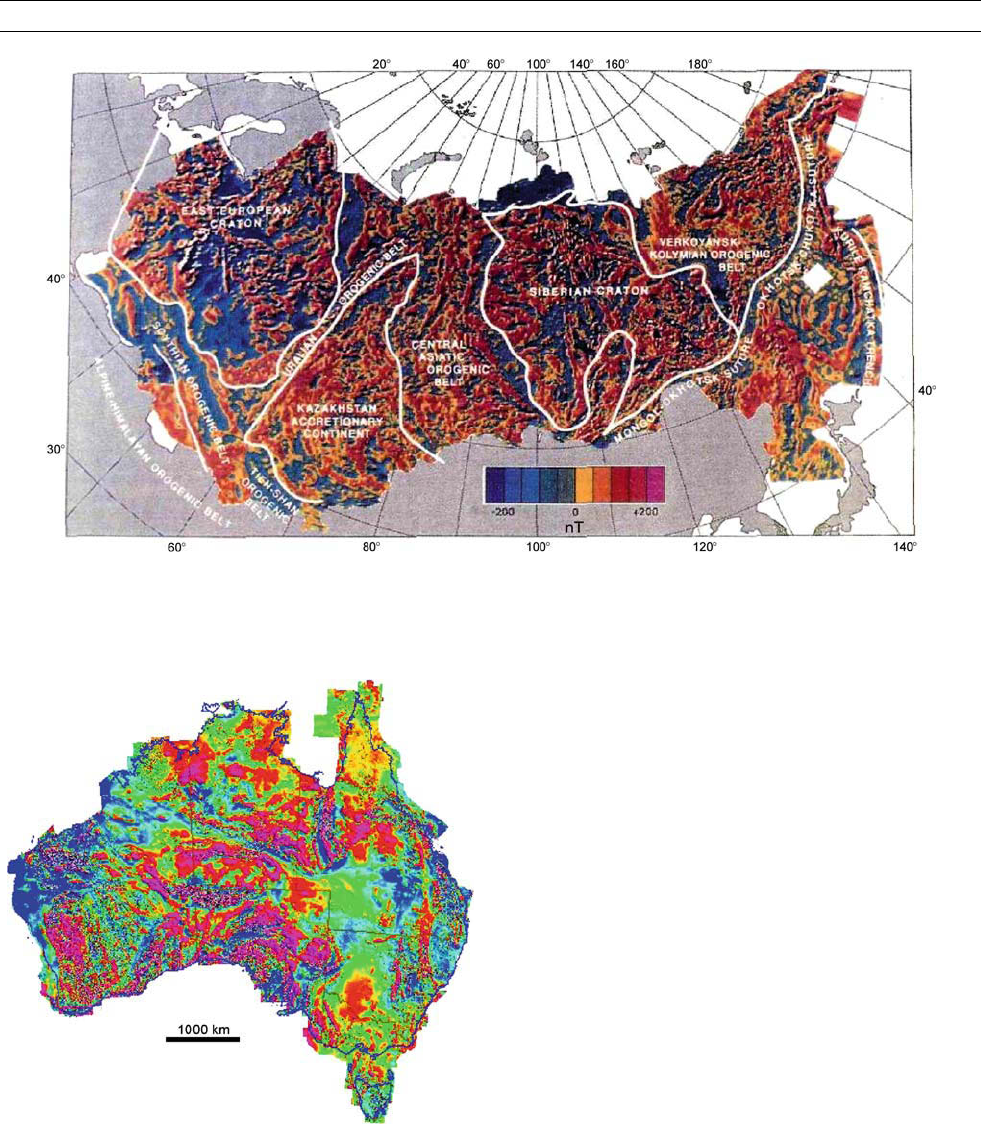
of geological complexity is revealed (Figure M3/Plate 7d; Zonenshain

et al., 1991), reflecting repeated orogenesis (mountain building) and

metamorphism since the time of the oldest known rocks, dating from

the Archean. The patterns of repeated continental collisions and

separations evident from more recent geology can be extrapolated into

this past. However, poor rock exposure in most of the oldest, worn-

down areas of the world (Precambrian shields) hampers their geologi-

cal exploration. Aeromagnetic surveys assist markedly here, though

understanding at the scale of whole continents often necessitates maps

extending across many national frontiers, as well as across oceans

where present continents were formally juxtaposed.

What holds for investigations into geology and resources over

regions or areas quite locally (say, scale 1:250000, a scale typical for

geological reconnaissance) also holds for national compilations of

larger countries (say scale 1:1000000) and at continental scale (1:5

million or 1:10 million). Magnetic anomaly mapping is arguably even

more useful at such scales since it represents unequivocal physical data

coverage, part of a nation’s (or a continent’s) geoscience data-

infrastructure. The view it offers to the geological foundations of con-

tinents is therefore of prime importance to improved understanding of

global geology. Repeated cycles of continental collision, coalescence,

and rifting-apart have led to the present-day arrangement of the

igneous and metamorphic rocks of the continental crust, as revealed

in continental scale images of magnetic anomalies, such as Australia

(Figure M4/Plate 7a; Milligan and Tarlowski, 1999).

Continental and global compilations of

magnetic anomalies

(Aero-)magnetic surveys usually record only the total strength of the

magnetic field at any given point, thus avoiding the need for any pre-

cision orientation of the magnetometer. After suitable corrections have

been applied for temporal field variations during the weeks or months

of a survey, subtraction of the long wavelength (more than several

hundred kilometers) components of the field leaves local anomalous

values that should be comparable from one survey to another. Thus

it is possible—though, in practice, challenging—to link many hun-

dreds of surveys together to make national or continental scale

coverages (Tarlowski et al., 1996; Fairhead et al., 1997).

The long wavelength components of magnetic anomalies must be

defined in an internationally coherent way, for which purpose the

IGRF (q.v.) was designed and is periodically updated by IAGA.

Anomaly definitions still vary greatly between surveys for various

Figure M2/Plate 9e Magnetic anomaly patterns in the North

Atlantic Ocean showing the symmetry of the anomalies either side

of the mid-Atlantic Ridge in the vicinity of Iceland. (Detail from

Verhoef et al., 1996, courtesy of the Geological Survey of Canada).

478 MAGNETIC ANOMALIES FOR GEOLOGY AND RESOURCES

reasons and, in addition to consistent use of the IGRF, national and

international cooperation is require d to link and level together the vari-

ety of magnetic surveys to a common level. Magnetic anomaly data

exist over most of the Earth ’ s surface, mostly a patchwork of airborne

surveys on land and marine traverses at sea (Reeves et al., 1998). In

2003, IAGA appointed a Task Group to oversee the compilation of such

a global magnetic anomaly map (www.ngdc.noaa.gov/IAGA/vmod/

TaskGroupWDMAM-04July12 s.pdf) that endeavors to complete its

work in time for the 2007 IUGG General Assembly.

Magnetic mineralogy

The physical link between geological formations and their magnetic

anomalies is the magnetic properties of rocks (Clark and Emerson,

1999). These are often measured, for example, in connection with

Ocean Drilling Program (ODP) analyses, paleomagnetic studies,

geological mapping, and mineral prospecting. ODP data provide local

information at widespread oceanic locations giving a global coverage.

International paleomagnetic databases represent the remanent magnetic

properties acquired in the geological past (see Paleomagnetism). Mag-

netomineralogical studies reveal that by far the most common mag-

netic source mineral of Precambrian shield areas is magnetite. So far,

the largest national campaign of magnetic property mapping was that

carried out in the former Soviet Union. The results were presented as

analog maps. Most of the world’s resource of digital petrophysical

data for the continents was collected in the Fennoscandian Shield by

the Nordic countries (Korhonen et al., 2002a,b). Even so, these data

represent only a small part of the crystalline basement of NW Europe.

More, similar data sets are required if we are to understand how well

this information represents crustal rocks more globally.

The results from Fennoscandia show that, when plotted on a dia-

gram of induced magnetization against density (Figure M5a) the sam-

ples form two populations, A and B. Population A represents the

paramagnetic range of susceptibilities defined by Curie’s law. Compo-

sitional variation of Fe- and Mn-oxides correlates with density, the

denser, more basic (mafic) rock lithologies being more magnetic than

acid (silicic) ones by up to an order of magnitude. This population is

only capable of causing anomalies less than about 25 nT, however.

A second population of rocks (B), mostly acid in chemistry, represents

the ferrimagnetic range of susceptibilities, mainly due to variations in

the abundance and grain size of magnetite. This population is two

Figure M3/Plate 7d Magnetic anomaly patterns recorded in aeromagnetic surveys over the former Soviet Union with the outlines of

some major tectonic domains added. Russia. (From Zonenshain et al., 1991, courtesy of the American Geophysical Union).

Figure M4/Plate 7a Magnetic Anomaly Map of Australia, 3rd edn

(Milligan and Tarlowski, 1999). (Courtesy of Geoscience

Australia).

MAGNETIC ANOMALIES FOR GEOLOGY AND RESOURCES 479

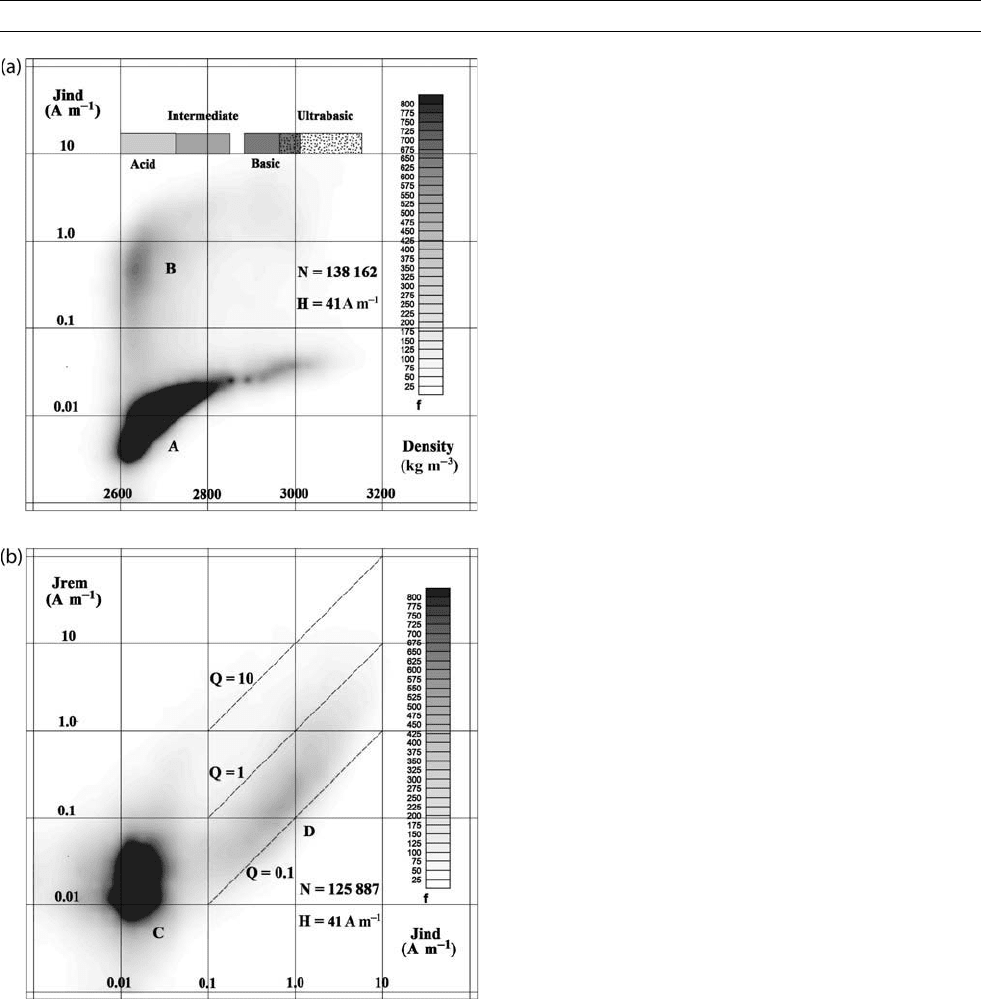
orders of magnitude more magnetic than the average of the first popu-

lation (A). Population B rocks represent most sources of local, induced

magnetic anomalies. Average susceptibilities vary typically from 0.04

to 0.02 SI units for these ferrimagnetic geological formations, but

much variation is found from one formation to another.

Another important parameter is the relative proportion of ferrimag-

netic (population B) rocks to the effectively “nonmagnetic” paramag-

netic (population A) rocks in any given area. For example, it is only

a few percent in the magnetic “low” of central Fennoscandia

but almost 100% in the northern Fennoscandian “high.” Overall in

Fennoscandia the average value is about 25%. In oceanic areas, by

contrast, it approaches 100%.

Spatial contrasts in magnetic rock properties that give rise to the

local magnetic anomalies encountered in mineral exploration are attri-

butable to such factors as (a) the aforementioned bimodal nature of

magnetic mineralogy (populations A and B), (b) the effects of mag-

netic mineralogy and grain size, (c) the history of magnetization and

demagnetization, and (d) the variation between induced and remanent

magnetization. These are related in turn to geological causes such as

initial rock lithology, chemical composition, oxygen fugacity, and

metamorphic history.

The ratio of remanent to induced magnetization varies typically

from 0.1 to 20, corresponding to rocks containing coarse-grained fresh

magnetite (most susceptible to induced magnetization) via altered and

fine-grained magnetites to pyrrhotite (with a very stable remanent

magnetization). Figure M5b shows the results for induced and rema-

nent magnetization from the Fennoscandian Shield. For the relatively

few rock samples (population D) that depart from a low level of mag-

netization (population C), the Q-ratio is mostly less than 1.0, indicat-

ing the predominance of induced magnetization over remanent as a

source of magnetic anomalies. A few exceptions are, however, highly

magnetic (above 1.0 A m

–1

). For increasingly large source bodies, var-

iations in the direction of all local remanent magnetizations cause the

net remanent magnetization to sum up more slowly than the consis-

tently oriented induced magnetization. Hence the effects of remanent

magnetization are relatively more important in magnetic anomalies

measured close to source bodies (such as on the ground) than farther

away (from an aircraft or satellite). This effect is even more noticeable

at magnetizations above 1 A m

1

, where Q-values tend to approach or

even exceed 1.0 (Figure M5b).

Colin Reeves and Juha V. Korhonen

Bibliography

Clark, D.A., and Emerson, D.W., 1991. Notes on rock magnetisation

characteristics in applied geophysical studies. Exploration Geophy-

sics, 22: 547–555.

Fairhead, J.D., Misener, D.J., Green, C.M., Bainbridge, G., and Reford,

S.W., 1997. Large scale compilation of magnetic, gravity, radio-

metric and electromagnetic data: the new exploration strategy for

the 90s (Paper 103). In Gubbins, A.G. (ed.), Proceedings of Explora-

tion‘97: Fourth Decenniel International Conference on Mineral

Exploration, Toronto, September 15–18, GEO/FX, 1068pp.

Korhonen, J.V., Aaro, S., All, T., Elo, S., Haller, L.Å., Kääriäinen, J.,

Kulinich, A., Skilbrei, J.R., Solheim, D., Säävuori, H., Vaher, R.,

Zhdanova, L., and Koistinen, T., 2002a. Bouguer Anomaly Map

of the Fennoscandian Shield 1:2000000. Geological Surveys of

Finland, Norway and Sweden and Ministry of Natural Resources

of Russian Federation. ISBN 951-960-818-7.

Korhonen, J.V., Aaro. S., All, T., Nevanlinna, H., Skilbrei, J.R., Sää-

vuori, H., Vaher, R., Zhdanova, L., and Koistinen, T., 2002b. Mag-

netic Anomaly Map of the Fennoscandian Shield 1:2000000.

Geological Surveys of Finland, Norway and Sweden and Ministry

of Natural Resources of Russian Federation. ISBN 951-690-817-9.

Figure M5 (a) Bulk density and induced magnetization in the

Fennoscandian Shield (redrawn from Korhonen et al. 2002a). The

lower population (A) contains the majority of rock samples, and

represents the paramagnetic range of susceptibilities defined by

Curie’s law. A second population of rocks (B), mostly acid in

chemistry, represents the ferrimagnetic range of susceptibilities,

due mainly to variations in the abundance and grain size of

magnetite. This population is two orders of magnitude more

magnetic than the average of the first population (A). (b) Induced

and remanent magnetization in the Fennoscandian Shield

(redrawn from Korhonen et al., 2002b). For the relatively few rock

samples (D) that depart from a low level of magnetization (C), the

Q-ratio is mostly less than 1.0, indicating the predominance of

induced magnetization over remanent. A few exceptions are,

however, highly magnetic. (Courtesy of Geological Surveys of

Finland, Norway, and Sweden and the Ministry of Natural

Resources of the Russian Federation).

480 MAGNETIC ANOMALIES FOR GEOLOGY AND RESOURCES

Milligan, P.R., and Tarlowski, C., 1999. Magnetic Anomaly Map of

Australia, 3rd edn, 1:5000000. Geoscience Australia, Canberra.

Reeves, C., Macnab, R., and Maschenkov, S., 1998. Compiling all the

world’s magnetic anomalies. EOS, Transactions of the American

Geophysical Union, 79: 338.

Tarlowski, C., McEwin, A.J., Reeves, C.V., and Barton, C.E., 1996.

Dewarping the composite aeromagnetic anomaly map of Australia

using control traverses and base stations. Geophysics, 61:

696–705.

Verhoef, J., Macnab, R., Roest, W. et al., 1996. Magnetic anomalies,

Arctic and North Atlantic Oceans and adjacent land areas. Geologi-

cal Survey of Canada Open File, 3282c.

Zonenshain, L.P., Verhoef, J., Macnab, R., and Meyers, R., 1991.

Magnetic imprints of continental accretion in the USSR. EOS,

Transactions of the American Geophysical Union, 72: 305, 310.

Cross-references

Aeromagnetic Surveying

IGRF, International Geomagnetic Reference Field

Paleomagnetism

Vine-Matthews-Morley Hypothesis

MAGNETIC ANOMALIES, LONG WAVELENGTH

Long-wavelength anomalies are static or slowly varying features of the

geomagnetic field, and originate largely within the lithosphere. These

anomalies stand in contrast to the rapidly time varying features charac-

teristic of even longer wavelengths, which originate within the outer

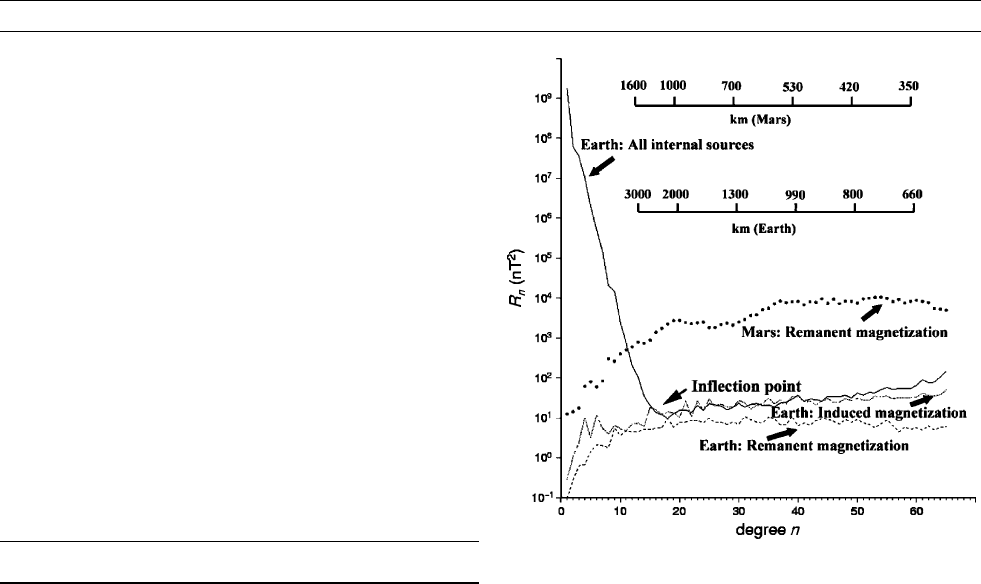
core. An inflection point, or change of slope, in the geomagnetic

power spectrum (Figure M6) can be seen at degree 13 and is a mani-

festation of the relatively sharp transition from core-dominated

processes to lithospheric-dominated processes. Long-wavelength

anomalies (Figure M7a/Plate 5c) are most easily recognized from

near-Earth satellites at altitudes of 350–750 km, and these altitudes

define the shortest wavelengths traditionally associated with such geo-

magnetic features. The lithospheric origin of these features was firmly

established by comparison with the marine magnetic record of seafloor

spreading in the North Atlantic (LaBrecque and Raymond, 1985). Vir-

tually identical features have now been recognized in satellite mag-

netic field records from POGO (1967–1971), Magsat (1979–1980),

Ørsted (1999–), and CHAMP (2000–). Long-wavelength anomalies

were first recognized by Cain and coworkers in about 1970 on the

basis of total field residuals of POGO data.

Although electrical conductivity contrasts (Grammatica and Tarits,

2002) and motional induction of oceanic currents (Vivier et al.,

2004) can produce quasistatic long-wavelength anomalies, the largest

contributors to long-wavelength anomalies are induced (M

) and rema-

nent (M

) magnetization in the Earth’s crust. Contributions from the

uppermost mantle may also be of importance, at depths where tem-

peratures do not exceed the Curie temperature (T

) of the relevant mag-

netic mineral. The earth’s main field (H ) is the inducing magnetic

field responsible for induced magnetization of lithospheric materials.

¼ kH expresses the linear relationship between the inducing field

and induced magnetization, true for small changes in the inducing

field. k is the volume magnetic susceptibility, treated here as a dimen-

sionless scalar quantity, and reflects the ease with which a material

is magnetized. If M does not return to zero in the absence of H,

the resulting magnetic field is said to be remanent or permanent. Thus

M ¼ M

þ M

, and the relative strength of the two contributions is

referred to as the Koenigsberger ratio or Q ¼ M

Inversions of long-wavelength anomaly observations into litho-

spheric source functions, for example magnetic crustal thickness

(Figure M7b/Plate 5d) are subject to many caveats. Simple solutions

are preferred, which also agree with other independently determined

lithospheric properties. Specific caveats with respect to inversions of

these magnetic field observations are that (1) direct inversion, in the

absence of priors, can uniquely determine only an integrated magneti-

zation contrast, (2) a remarkably diverse assemblage of magnetic anni-

hilators (Maus and Haak, 2003) exist, which produce vanishingly

small magnetic fields above the surface, and (3) the longest wave-

length lithospheric magnetic signals are obscured by overlap with the

core and it is formally impossible to separate them.

Unresolved research questions include (1) the continuing difficulty of

signal separation, especially with respect to external fields (Sabaka

et al., 2004), and the particular problem of resolving north-south features

from polar-orbiting satellites, (2) the relative importance of magnetic

crustal thickness variations and magnetic susceptibility variations in

producing long-wavelength anomalies, (3) the relative proportions of

induced and remanent magnetization in the continents and oceans,

(4) the mismatch between the observed long-wavelength fields at satellite

altitude, and surface fields upward continued to satellite altitude, (5) the

separation of long-wavelength anomalies caused by motional induction

of large-scale ocean currents, (6) the isolation and relative importance

of shorter wavelength anomalies (between 660 and 100 km wavelength),

and finally (7) the origin of the order of magnitude difference between

the observed lithospheric magnetic fields of the Earth and Mars.

Michael E. Purucker

Figure M6 Comparison of the Lowes-Mauersberger (R

) spectra at

the surface of the Earth and Mars for a variety of internal fields.

The inflection point in the terrestrial power spectra represents the

sharp transition from core processes at low n to lithospheric

processes at higher n. R

is the mean square amplitude of the

magnetic field over a sphere produced by harmonics of degree n.

The terrestrial spectrum of all internal sources comes from Sabaka

et al. (2004), the Martian remanent spectrum is derived from

Langlais et al. (2004), the terrestrial induced spectrum is derived

from Fox Maule et al. (2005), and the terrestrial remanent

magnetization spectrum (of the oceans, and hence a minimum

value) was derived from Dyment and Arkani-Hamed (1998).

MAGNETIC ANOMALIES, LONG WAVELENGTH 481

Figure M7/Plate 5c,d Long-wavelength anomalies (a) in the total field as seen by the CHAMP magnetic field satellite at an altitude of

400 km (MF-4 model of GFZ-Potsdam available at www.gfz-potsdam.de/pb2/pb23/SatMag/model.html). Spherical harmonic degrees

between 16 and 90 are included within this map. The magnetic crustal thickness (b), derived as described in Fox Maule et al. (2005),

explains the observations in (a). The map uses as a starting model the 3SMAC (Nataf and Ricard, 1996) compositional and thermal

model of the crust and mantle. 3SMAC is modified in an iterative fashion with the satellite data, after first removing a model of the

oceanic remanent magnetization (Dyment and Arkani-Hamed, 1998), until the magnetic field predicted by the model matches the

observed magnetic field. A unique solution is obtained by assuming that induced magnetizations dominate in continental crust, and

that vertical thickness variations dominate over lateral susceptibility variations (Purucker et al., 2002). A starting model such as

provided by 3SMAC is necessary to constrain wavelengths longer than about 2600 km. Longer wavelengths are obscured by overlap

with the core field. The white lines delineate plate boundaries, transform faults, and mid-ocean ridges. Illumination on these shaded

relief maps is from the east.

482 MAGNETIC ANOMALIES, LONG WAVELENGTH

Bibliography

Dyment, J., and Arkani-Hamed, J., 1998. Contribution of lithospheric

remanent magnetization to satellite magnetic anomalies over the

world’s oceans. Journal of Geophysical Research, 103: 15423–

15441.

Fox Maule, C., Purucker, M., Olsen, N., and Mosegaard, K., 2005.

Heat flux anomalies in Antarctica revealed by satellite magnetic

data. Science, 10.1126/science.1106888.

Grammatica, N., and Tarits, P., 2002. Contribution at satellite altitude

of electromagnetically induced anomalies arising from a three-

dimensional heterogeneously conducting Earth, using SQ as an

inducing source field. Geophysical Journal International, 151:

913–923.

LaBrecque, J.L., and Raymond, C.A., 1985. Seafloor spreading

anomalies in the MAGSAT field of the North Atlantic. Journal of

Geophysical Research, 90: 2565–2575.

Langel, R.A., and Hinze, W.J., 1998. The Magnetic Field of the

Earth’s Lithosphere. Cambridge: Cambridge University Press.

Langlais, B., Purucker, M., and Mandea, M., 2004. Crustal magnetic

field of Mars. Journal of Geophysical Research, 109: E02008,

doi:10.1029/2003JE002048.

Maus, S., and Haak, V., 2003. Magnetic field annihilators: invisible

magnetisation at the magnetic equator. Geophysical Journal Inter-

national, 155: 509–513.

Nataf, H., and Ricard, Y., 1996. 3SMAC: an a priori tomographic

model of the upper mantle based on geophysical modeling. Physics

of the Earth and Planetary Interiors, 95: 101–122.

Purucker, M., Langlais, B., Olsen, N., Hulot, G., and Mandea, M.,

2002. The southern edge of cratonic North America: evidence from

new satellite magnetometer observations. Geophysical Research

Letters, 29(15): 8000, doi:10.1029/2001GL013645.

Sabaka, T.J., Olsen, N., and Purucker, M., 2004. Extending compre-

hensive models of the Earth’s magnetic field with Ørsted and

CHAMP data. Geophysical Journal International, 159: 521–547.

Vivier, F., Maier-Reimer, E., and Tyler, R.H., 2004. Simulations of

magnetic fields generated by the Antarctic Circumpolar Current

at satellite altitude: can geomagnetic measurements be used to

monitor the flow? Geophysical Research Letters, 31: L10306,

doi:10.1029/2004GL019804.

Cross-references

CHAMP

Harmonics, Spherical

Magnetic Anomalies, Marine

Magnetic Field of Mars

Magnetic Surveys, Marine

Magsat

Ørsted

POGO (OGO-2, -4, and -6 spacecraft)

MAGNETIC ANOMALIES, MARINE

Magnetic anomalies are perturbations of the geomagnetic field due to

Earth structure. They are seen when one subtracts a regional magnetic

field from a series of observed readings. They have a different charac-

ter over surface of the deep oceans than on they do on land. The

unique nature of marine magnetic anomalies became apparent in the

early 1950s when submarine detecting magnetometers were used for

geophysical exploration by research ships. Over the oceans important

marine anomalies may have an amplitude of a few tens to a few hun-

dreds nanotesla and a wavelength of about 100 km, depending upon

the depth of water. Previously some geomagnetic field measurements

had been made on nonmagnetic ships but these readings were taken

so far apart that the short anomalies were not defined. A few aircraft

measurements had been made but they were high above the ocean sur-

face reducing the size of the anomaly or were made over the continen-

tal shelf where anomalies have a different character from those in the

deep ocean.

Early observations of marine anomalies

When research ships started taking measurements the magnetometer

was towed behind the ship so the magnetic materials of which the ship

was constructed did not influence the readings. Furthermore the inten-

sity of the field, rather than its directional components, was measured

thereby eliminating the need to know the orientation of the magnet-

ometer. The first generation of marine magnetometers was of the flux-

gate type, which had a small oriented special metal core. This core was

mechanically oriented in the direction of the Earth’s field by nulling

the field measured by secondary cores, which were at right angles to

the main core. This arrangement, while awkward, was used at sea

for several years. The first systematic survey at sea was made by

Scripps Institute of Oceanography using a fluxgate magnetometer

towed by a Coast and Geodetic Survey ship in the Pacific Ocean off

the western United States. When a regional magnetic field was sub-

tracted from the observed field to get the anomalies, these anomalies

were seen to be linear patterns, oriented nearly north-south, but with

occasional sharp east-west offsets in the linear pattern (Vacquier,

1959). The source of these linear anomalies was unknown because

there was no obvious seafloor feature, which could cause them.

At about the same time as the Pacific measurements were made mis-

cellaneous cruise measurements off the US east coast, near the conti-

nental shelf showed major marine magnetic anomalies which were

subparallel to the coast. They turned onto land and split into several

parts over the states of Georgia and Florida.

Early shipboard measurements had shown a large magnetic anomaly

over the center of the mid-Atlantic Ridge in several places. To investigate

this in a systematic way, a low-level aeromagnetic survey was made over

the part of the Reykjanes Ridge south of Iceland (Figure M8) (the

Reykjanes, using a US Naval Oceanographic Office aircraft flying out

of southern Iceland; Heirtzler et al., 1966). This survey also showed linear

anomalies, paralleling the ridge axis and symmetrically located about the

axis of the Reykjanes Ridge. This suggested that the origin of these linear

anomalies was related to the structure of the ridge.

The origin of the anomalies

In 1963, while the Reykjanes Ridge was being flown, an important

paper was published by Fred Vine and Drummond Matthews (Vine

and Matthews, 1963) pointing out that the linear anomalies in the

ocean might be caused by normally and reversely magnetized rocks

of the ocean floor. These authors suggested, furthermore, that these

rocks can be represented by magnetized blocks and they may have

acquired their magnetization when they were extruded at the axis of

the mid-ocean ridge in times past. Presumably the blocks moved out

from both sides of the ridge. This is the basis of the seafloor spreading

theory. The magnetism was acquired at the axis, while the upwelling

magma cooled. It is called remanent magnetization. As the material

moves away from the axis it is in the ambient geomagnetic field and

so secondary magnetism is induced in the rocks. That is called induced

magnetization. Thus, the magnetization has two components, although

the remanent component is usually stronger.

Applying Vine-Matthews theory to the Reykjanes Ridge data and

knowing the times of the most recent few reversals of the field it

was possible to learn that the seafloor of the Reykjanes Ridge is

spreading at about 1.5 cm y

–1

away from the ridge axis. Reykjanes

Ridge anomalies which were further from the axis allowed one, for

the first time, to know the ages of the various reversals as far back

as 10 Ma, assuming that the seafloor spreading rate has been constant.

MAGNETIC ANOMALIES, MARINE 483

This knowledge of the relationship between marine magnetic

anomalies, reversals of the geomagnetic field, and seafloor spreading

rates created a flurry of activity in marine geophysics in the 1960s.

A new simplified (proton precession) magnetometer was developed,

analytical methods were undertaken to relate the oceanic rocks to the

anomaly observed. Cruises were undertaken in many parts of the

world to extend the geomagnetic reversal timescale and to study sea-

floor spreading and the tectonics of the ocean floor. (See Figure M9/

Plate 8: World map of isochrons of the ocean floor).

The rocks of the ocean floor are usually covered with a thick layer

of sediments. The sediments are weakly magnetized so they do not

interfere with the magnetic anomalies caused by the rocks beneath.

However, if a sediment core is taken and measured in the laboratory

it will also show reversals of past geomagnetic field directions just like

anomalies measured across the ocean surface. Thus one can date sedi-

ments using the timescale of geomagnetic field reversals.

Some geomagnetic field anomalies can be observed by magnetic

field satellites in near-Earth orbit, although anomalies over the oceans

are small and difficult to analyze. Magnetic measurements have also

been made by magnetometers towed near the deep seafloor. These

have proved especially useful in studying the transition between

normally and reversely magnetized rocks.

Using magnetic anomalies to date the ocean floor

The age of the seafloor is related to the distance of the magnetized

blocks from the ridge axis, not the distance of the magnetic anomaly,

from the ridge axis. Thus it is necessary to see how the position of

the anomalies is related to the position of the source rocks. A computer

Figure M8 Marine magnetic anomalies over the Reykjanes Ridge

(RR) south of Iceland. Positive anomalies are shaded black (after

Heirtzler et al., 1966).

Figure M9/Plate 8 World map of isochrons of the ocean floor (after Muller et al., 2005).

484 MAGNETIC ANOMALIES, MARINE

program is commonly used to calculate the anomaly over a block.

These programs assume the block is infinitely long in some direction

(2D) rather than having a finite three-dimensional shape (3D), making

the calculation simpler. The shape of the source block is changed until

the calculated anomaly matches the observed anomaly. This technique

is called a forward anomaly calculation. It is inherently nonunique in

that several different shapes may cause the same anomaly. Other types

of programs assign one dimension, for example the thickness, and then

use the observed anomalies to locate the source body. Other programs

convert the observed spatial series to a frequency spectrum and filter

the spectrum to locate the bodies. It is also possible to mathematically

convert the observed anomaly series to show how it would look at the

magnetic pole. This transforme d anomaly will be directly over its

causative body.

Normal and reverse intervals of the geomagnetic field occur at irre-

gular time intervals creating a pattern of magnetic anomalies with irre-

gular spacing. Since this same irregular pattern is found in the different

oceans of the world it aids in dating the anomalies in one ocean if they

were already dated in another ocean. To refer to anomalies along

an anomaly profile, the anomalies have been given numbers 1 (at

the axis) to 34 (about 83 Ma). Intermediate intervals are assigned a

“chron” notation (see Geomagnetic polarity timescale, q.v.).

Older marine magnetic anomalies

Long shipboard magnetic profiles extending across the oceans showed

a similar sequence of magnetic anomalies, although the shape varies a

bit with latitude and the azimuth of the magnetic lineation. This sug-

gested that seafloor spreading had been constant in each major ocean,

although the spreading rate may be different from one ocean to

another. In the South Atlantic anomaly 34 is close to the continental

margins of South America and South Africa, indicating that the South

Atlantic Ocean opened about 83 Ma ago. In the North Atlantic anom-

aly 34 does not reach the continental margins, because the North

Atlantic Ocean is older than the South Atlantic Ocean.

In the Northwest Pacific the anomalies are linear but not subparallel

to existing spreading centers. The spreading center, which created

them, has since disappeared and the seafloor spreading has changed

direction. Many are older than anomaly 34 and are assigned a number

prefixed by the letter M to show that they be part of another (Meso-

zoic) series. Near the edges of the Pacific Ocean there are subduction

zones where the seafloor turns under the continents. The magnetic

anomaly pattern is extinguished at these subduction zones, such as

off Alaska, off the Aleutians, off Japan, and at the Kermadac Trench

north of New Zealand. It was found that, in the South Pacific Ocean,

anomalies are symmetric about the ridge axis, even when the anoma-

lies are separated by more than 1000 km. The Indian Ocean and the

Arctic Ocean south of Australia abound with dated magnetic anoma-

lies, although the oldest are not as old as the oldest in the Northwest

Pacific.

By using a long profile in the South Atlantic Ocean the sequence of

magnetic reversals (geomagnetic timescale) were originally deter-

mined for the last 80 Ma, where there were 171 reversals. By compar-

isons with dated rocks from the seafloor the original geomagnetic

timescale has been slightly revised (Cande and Kent, 1995).

James R. Heirtzler

Bibliography

Cande, S.C., and Kent, D.V., 1995. Revised calibration of the geomag-

netic polarity timescale for the late Cretaceous and Cenozoic.

Journal of Geophysical Research, 100: 6093–6095.

Heirtzler, J.R., LePichon, and Xavier Gregory, B.J., 1966. Magnetic

anomalies over the Reykjanes Ridge. Deep-Sea Research, 13:

427–443.

Muller, R.D., Roest, W.R., Royer, Y.-Y., Gahagan, L.M., and Sclater,

J.G., 2005. Digital isochrons of the ocean floor. Available at:

htto://gdcinfo.agg.nrcan.gc.ca/app/images/agemap.gif

Vacquier, V.V., 1959. Measurement of horizontal displacements along

faults in the ocean floor. Nature, 183: 452–453.

Vine, F.J., and Matthews, D.H., Magnetic anomalies over oceanic

ridges. Nature, 199: 947–949.

Cross-references

Geomagnetic Polarity Timescale

Geomagnetic Polarity Timescales

Magnetization, Oceanic Crust

Magnetization, Remanent, Application

Seamount Magnetism

MAGNETIC ANOMALIES, MODELING

Introduction

The magnetic anomalies of planetary lithosp here reflect the lateral

variations of magnetization in the upper most part of the lithosphere

that is colder than the Curie temperature of its magnetic minerals.

The variations may arise from several processes, such as intrusive

bodies with different magnetization than the country rocks, the juxta-

position of crustal blocks of different magnetization through plate tec-

tonics, and the creation of the oceanic crust during different core field

polarity periods.

A magnetic anomaly is the projection of the magnetic field of a

body in the direction of the local geomagnetic field. The measured

magnetic data have contributions from the core field, the lithospheric

field, the external field, the field arising from the induced currents in

the mantle because of the time variations of the external field, and

the measurement errors. The core and the lithospheric fields are

time-invariant within a few years, while the external field is strongly

time-dependent. A time-varying external field with a period of t is

translated to a special variation of wavelength l ¼ tv when the mag-

netic data is acquired by a vehicle (airplane, ship, or satellite) moving

at speed v, and contaminates the lithospheric field of the same wave-

length. To avoid the contamination, the magnetic data acquired during

the quiet times of the external field are generally used. The core field,

with amplitudes ranging from 30000 to 70000 nT, dominates the litho-

spheric field, which has usually an amplitude of a few hundred nano-

tesla near the surface and less than 20 nT at satellite altitudes of

400 km. The instrument errors are nowadays negligible, but the mea-

surement error can be appreciable especially for the satellite magnetic

data. An attitude error of only 10

in the orientation of the coordinate

axes fixed to a satellite can produce an error on the order of 2–4nT,

depending on the satellite’s latitude, which is comparable to a vec-

tor component of the lithospheric magnetic field at the satellite eleva-

tions. One possible way of removing the error arising from the attitude

is to use the magnetic intensity data, which is independent of the orien-

tation of the coordinate system. Let

F denote the measured magnetic

field and assume that it consists of the core field

B and the lithospheric

field

f , ignoring the external field. Then

Fj¼j

B þ

f j (Eq. 1)

The magnetic anomaly T is the difference between the intensity of the

observed field and that of the local core field,

T ¼j

Fjj

Bj (Eq. 2)

MAGNETIC ANOMALIES, MODELING 485