Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

coefficient where neutral species are involved. However, if electric fields

are involved and charge buildup can occur, this factor may play a signifi-

cant role in determining the diffusion coefficient. However, as described

above, the solid solubility will determine the amount of material that can

be dissolved or rejected by the film (or the substrate), the compound for-

mation, if any, and the segregation at the film-substrate interface and at

the grain boundaries of the polycrystalline films.

[29]

Segregation at the Grain Boundaries and Interfaces

When a solute is added to a polycrystalline solid, the concentration of

the solute in the grain (or the bulk of the crystal) is controlled by the solid

solubility (that is, the solubility maximum) at the given temperature.

However, the concentration maximum of the solute in the grain boundaries

depends on several factors.

[23, 30]

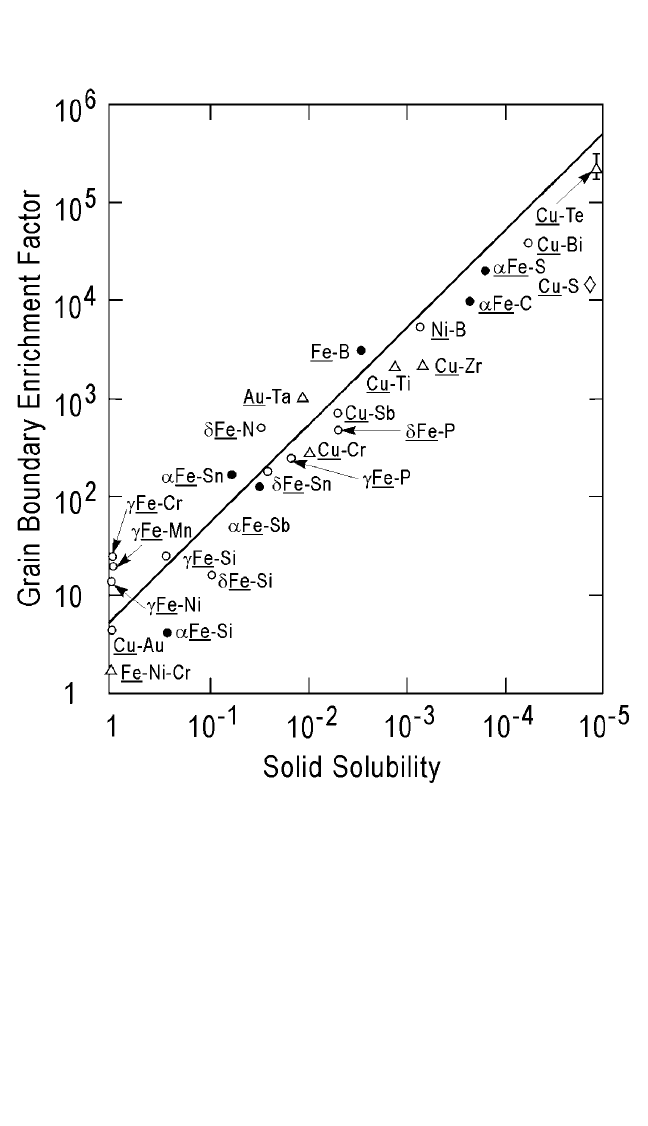
We define an enrichment factor E

as:





 .

Several investigators

[31–33]

have concluded that the lower the atomic solid

solubility is in the grains (or bulk), the larger E

is. Figure 5.2 shows the

classical plot of the measured E

as a function of the atomic solubility.

[31]

Lower bulk solubility leads to a higher rejection (of solute) into the grain

boundaries. Note that at such high concentrations of impurities (in grain

boundaries), a thin layer (or small volume) of a new phase may form

in the grain boundary. Impurities of one type can also control the concen-

tration of some other undesirable impurities. An example of this is the

addition of Al to steels. Although Al primarily controls the oxygen in solu-

tion in liquid steel, it also controls grain size and shape through the for-

mation of aluminum nitride particles that retard the motion of selected

grain boundaries.

[32]

Similarly, small amounts of Cu added to Al are known

to segregate in the grain boundaries and form q phase-particles, thus

enhancing the electromigration lifetime of such interconnects. The con-

clusion is that the impurity with the lowest atomic solid solubilities should

be used if we want to “stuff” grain boundaries.

[2]

Experience, described in

the preceding examples, has shown that grain boundary stuffing leads to

considerably reduced diffusion and metallurgical interactions, which are

predominantly controlled by grain boundary diffusion, especially at low

temperatures.

[33]

A theoretical framework exists to rationalize the observations and to

characterize broadly the behavior observed. Examine the problem as

Solute concentration in the grain boundaries



Solute concentration in grains

252 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_05.qxd 11/29/04 6:19 PM Page 252

DIFFUSION BARRIERS IN SEMICONDUCTOR DEVICES, MURARKA 253

composed of two, two-phase systems: the thin-film/boundary system and

the APDB/boundary system. Segregation of the impurity to the boundary

region is driven by the free energy of segregation that has been derived by

McLean.

[34]

Consider a lattice made up of N undistorted surface sites with

P solute (impurity) atoms distributed on them. Also consider n distorted

surface sites with p solute atoms distributed among them. If the energy of

the solute on the lattice is E, and the energy of the solute on the surface is e,

Figure 5.2 Correlation of grain boundary enrichment (ratio of concentration of the

grain boundary to the grain) factor with the atomic solid solubility.

Note: From E. D. Hondros, J. Phys. 36: coll. C-117 (1975); M. P. Seah and E. D. Hondros, Proc. R.

Soc. London, A335:191 (1973); and D. Gupta, Metall. Trans., 8A:1431 (1977)]

Ch_05.qxd 11/29/04 6:19 PM Page 253

then the free energy of the system is:

G  pe  PE  kt [ln(n!)N!  ln(n  p)!p!(N  P)!P!]. (13)

The minimum in G can be derived by differentiation with respect to p.

This results in the equation:

P(n  p)  [P(N  P) exp[(E  e)kt], (14)

or the more familiar:

(1  X

)  [X

(1  X

)] exp(∆Ekt), (15)

where X

is the adsorption level as a mole fraction of a monolayer, X

the solute mole fraction, and ∆E is the heat of adsorption of the segregant

at the boundary.

The extent of segregation at the interface boundary is thus determined

by ∆E and by the concentration of the solute (impurity) in the solvent. For

an ideal situation, for example, epitaxially grown silicon on silicon, ∆E

will be near zero and no segregation will occur at the interface. However,

dislocations have been found experimentally at this interface, resulting

from lattice parameter differences between the deposited layers and the

substrate arising from differences in impurity concentrations. In such a

case, ∆E is a positive quantity and will lead to some impurity segregation

even at the epitaxial interface.

The problem of a boundary separating two different materials presents

significant difficulties in modeling segregation behavior. One approach is

to treat each material separately with a common boundary. The thin film

has a segregation coefficient Θ

that is defined:

 X

X

, (16)

where X

is the fraction of impurity dissolved in the thin film. Similarly,

a segregation coefficient for the given underlying (or overlying) film,

such as an APDB film, can be defined:

ulf

 X

X

ulf

, (17)

where X

ulf

is the fraction of impurity in the given underlying film.

Therefore, the amount of impurity in the boundary between the thin film

and the underlying film can be viewed as the competition between the two

segregation coefficients. At equilibrium, the impurity concentration in the

boundary reflects the equilibration of the impurity levels in the two films

254 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_05.qxd 11/29/04 6:19 PM Page 254

DIFFUSION BARRIERS IN SEMICONDUCTOR DEVICES, MURARKA 255

in contact. In such a case, a segregation coefficient can be defined as a

ratio of the two interfacial segregation coefficients:

seg

 Θ

Θ

ulf

 X

ulf

X

, (18)

where K

seg

, usually known as the segregation coefficient between the two

thin-film materials, is truly a lattice segregation coefficient, in contrast to

the interfacial segregation coefficients Θ

ulf

and Θ

The segregation coefficient will thus control the equilibrium concen-

tration across the phase boundary. Precipitation of a new phase at the

phase boundary will, however, change the segregation behavior drasti-

cally. In thin films, the grain boundaries will contribute very significantly,

and possibly erratically, to the segregation phenomenon and thus to

desired APDB behavior.

Information on the solid solubilities can be obtained from the binary

phase diagrams. In cases where such information is not available, we can

make estimates based on a similar binary system or by using Hume-

Rothery rules.

[35]

One of these rules states that the extent of primary solid

solution is limited whenever the differences in the atomic radii of the sol-

vent and solute atoms exceed 15%. The larger the electronegativity dif-

ference is, the more stable the solid solution is. The crystalline structure

of the solids also influences the solubility limits. Experience has shown

that materials with similar crystal structures have extended mutual solid

solubility. These observations and rules on solid solubility apply to crys-

talline materials, where the lattice solubility greatly exceeds the contribu-

tion of defects, phase boundaries, or surfaces to the solute behavior. In

thin films, where grain boundaries and dislocations are abundant, the seg-

regation of impurities to these sites will, in general, control the total

amount of solute dissolved in such films. For example, large amounts of

arsenic and phosphorus could be present in the grain boundary regions of

polysilicon without affecting the electrical resistivity. Upon annealing at

high temperatures, larger amounts of dopant can dissolve into the silicon

grains, leading to a lower resistivity in subsequently quenched samples.

On slow cooling, the excess dopant is rejected to grain boundaries, leav-

ing behind a higher resistivity material.

[36]

Thus, the grain structure of the

films and the cooling rate will strongly affect the amount of solute

retained in the lattice and will thus determine the segregation and redis-

tribution behavior.

As far as thin-film reactions leading to compound formation are con-

cerned, the thermodynamic considerations correctly predict the outcome

of reactions. If the reaction leads to a decrease of total free energy, then

under suitable kinetic conditions, a reaction will proceed. On the other

hand, if the reaction does not lead to a lowering of free energy, it may not

Ch_05.qxd 11/29/04 6:19 PM Page 255

occur. Thus, by use of the free energy of formation data from thermody-

namics data in handbooks, we can safely predict the possibility of a reac-

tion occurring. In the absence of the free-energy data, we can use the heats

of formation to obtain a similar answer.

When a reaction between two metals occurs, the outcome generally is

a solid solution or one or more intermetallic compounds. Established

binary phase diagrams show the existence of such intermetallics. Even

with this knowledge, a realistic modeling of the interfacial reactions and

compound formation (and their impact on the properties) is very difficult

and complicated. An interfacial reaction can usually be treated as a binary

diffusion couple. For components of such a couple that exhibit a series of

equilibrium intermetallic phases across the alloy system, the prediction of

equilibrium thermodynamics is that the resultant diffusion zone will

include a series of bands with sharp boundaries, each band corresponding

to one of the intermetallics.

[37]

The width of a given band will depend on

a variety of competitive factors, such as the solubility range across the

phase and component diffusion coefficients within the band in relation to

those in adjacent phases. In this way, the chemical potential of each com-

ponent, the gradient of which is the fundamental driving force for diffusion,

will be continuous across the entire diffusion zone. Thus, at the interface

separating any pair of bands, say g and e, the chemical potentials are equal

for each component; that is, the phases at the interface may be in quasi-

equilibrium. However, the advanced state of reaction is, at best, only a ref-

erence point in relation to the initial reaction conditions.

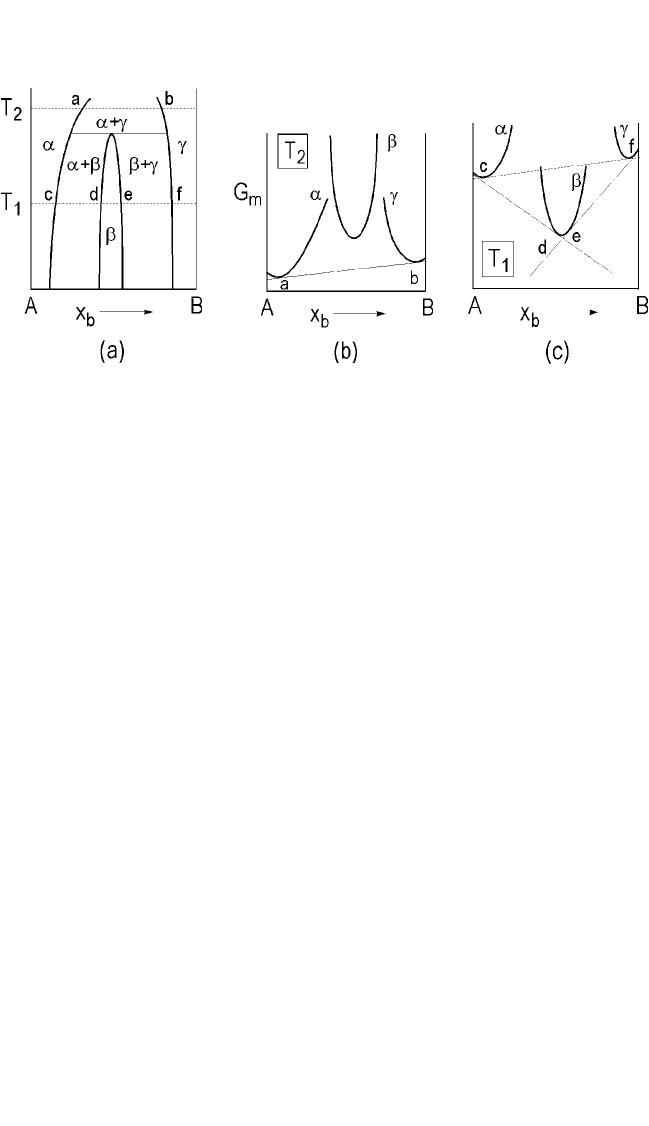
Figure 5.3(a) presents a portion of a binary equilibrium phase diagram

at constant pressure for a system A, B that forms a single intermetallic b.

The solid solubility limits for the thermal solid solutions a and g at tem-

perature T

are c and f, respectively. The intermetallic phase b exhibits a

range of solubility, d-e. The corresponding Gibbs free-energy-composition

diagram for this temperature is shown in Fig. 5.3(b) and (c), where the

common tangent construction, equivalent to the chemical potential equal-

ities of defining equilibrium, is included as solid straight lines. Note that

c, d, a, and f are points of tangency, with the metastable equilibrium a  g

indicated by the dashed common tangent. For this system, the reaction

a  g → b is a peritectoid reaction. Qualitatively, however, Fig. 5.3 would

be unchanged if the intermetallic b were congruently or peritectically

melting, rather than associated with a peritectoid reaction as shown.

In any event, this situation results from deposition of component B

(for example, copper) onto substrate A, at low enough temperature to pre-

vent any reaction during deposition. When a reaction does occur, limited

interdiffusion that creates terminal solutions very near the interface pre-

cedes the formation of any phase or phases. In such systems, a state of

metastable equilibrium involving a  g tends to be established first, a

256 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_05.qxd 11/29/04 6:19 PM Page 256

DIFFUSION BARRIERS IN SEMICONDUCTOR DEVICES, MURARKA 257

process that may be intercepted by nucleation of the intermetallic. This is

in contrast to the situation at the temperature T

(Fig. 5.3), which repre-

sents the stable state. With the formation of an intermetallic, as in the typ-

ical peritectoid case, the reacting components are physically separated as

the product phase forms. When the interface is covered with a new phase,

the thickening growth reaction requires diffusion through the intermetal-

lic layer, which may still be controlled by mass transport kinetics or by

interface reaction kinetics.

[37]

The actual situation, however, is usually quite different from such a

classical model. Realistic modeling of interfacial reactions and compound

formation require an analysis of experimental results obtained under

different conditions and for different combinations of layered diffusion

systems. Note that generally, not all the intermetallics reported in a phase

diagram are formed in thin-film couples. For example, in one of the com-

plex binary systems of Pt and Al, in thin-film reaction couples annealed in

the temperature range 200 to 500°C, only 6 of 12 possible phases were

detected.

[38]

In a relatively simple system of Ti reacting with silicon, only

three of the possible five phases have been reported.

[39]

On the other hand,

for the simple system of the thin-film couple of Mg and Cu, both reported

intermetallics have been detected.

[40]

Several factors determine the

absence of certain phases in thin-film couples: limited range of thickness,

atomic diffusivities in various phases, concentration gradients, tempera-

ture, free energies, impurities, nucleation and growth, and the amount of

material available during the interaction. The available amount of the

reacting material, measured by its thickness in films, also determines the

Figure 5.3. (a) Binary system A-B with one intermetallic; (b) and (c) molar free-

energy composition diagrams at T

and T

, respectively. Stable equilibrium is

shown by solid tangent and metastable equilibria by dashed lines.

Note: From C. W. Allen and A. G. Sargent, Mat. Res. Soc., 54:97 (1986).

Ch_05.qxd 11/29/04 6:20 PM Page 257

extent of intermetallic compound formed in the final product. Goselle and

[41]

have examined this aspect of the reaction between thin films, con-

sidering some of the factors mentioned here. The absence of the phases in

thin-film interaction products is explained on the basis of nucleation and

growth probabilities and diffusion across very thin phases that may not be

detected by the analytical techniques.

It is pointed out that the above-mentioned principles and discussions

also apply to ternary, quaternary, and other systems. However the phe-

nomena become very complicated, and reaction products difficult to predict.

Only experimental results, obtained under a defined set of conditions, pro-

vide an immediate answer.

Free Energy and Heat of Formation

Thermodynamic considerations predict the stability of a system under

given conditions. We are concerned about the adhesion of the APDB film

with the films it is separating under the conditions of forming such struc-

tures and in actual use. Afilm is said to adhere well to the substrate if all

film-substrate interfaces are not physically affected during the fabrication

or service, even when exposed to a reasonably high level of stress. Thus

to promote adhesion, we must ensure (1) excellent physical and chemical

bonding, preferably the latter, since it is energetically more favorable,

across the substrate-metal film interface, and (2) low levels of stress in the

film arising from the device/circuit fabrication processes. Reasonable

assumptions have led to the conclusion that for good adhesion, chemical

interactions leading to the interatomic bonding at the desired interface are

essential Such interactions must, however, be self-limiting so that only a

very thin layer (preferably a monolayer or two) of the interfacial reaction

product results. In addition, stresses must be kept below a level of

∼0.5 Gpa (5  10

dyn/cm

[42]

To ensure adhesion, we must also ensure

the absence of easy deformation/fracture modes, reactive environments

that produce stress, and long-term degradation modes.

For example, Al adheres well to oxides, nitrides, carbides, silicides, and

Si. On the other hand, copper does not bond well with the surfaces of the

same materials. The difference is reflected in the energies of formation of the

metal oxide, nitride, carbide, and silicide, or in the metal-nonmetal diatomic

bond strengths. It is thus apparent that the deposition of Cu directly on SiO

or on a typical polymer interlayer dielectric will not provide the needed adhe-

sion at the interface. Note, however, that the energies of formation of the Cu

fluoride and sulphate are high and are comparable to those of silicon com-

pounds, but are not as high as those of Al compounds. We can then postulate

that if the ILD surface is terminated in a (F) and/or (SO

) species, Cu may

258 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_05.qxd 11/29/04 6:20 PM Page 258

DIFFUSION BARRIERS IN SEMICONDUCTOR DEVICES, MURARKA 259

form bonds with such species and thus form an interfacial layer to provide

the necessary adhesion between the ILD and Cu. Thicker interfacial layers of

these types should, however, be avoided to eliminate the tendency of crys-

tallization of these compounds at the interface.

Temperature

Temperature is perhaps the most important parameter in determining

the need and usefulness of the APDB between two films it is separating.

Our goal is to process sets of films under optimized process conditions,

then to use the product under so-called operating conditions. We can

either choose the process and use a temperature/time combination to suit

the given APDB, or select the APDB to survive the given process and tem-

perature/time combination. Classically, a 450°C, 30- to 60-minute annealing

in hydrogen-containing ambients has been used for Al metallization

schemes. Presently, Cu has replaced A, and new low-dielectric-constant

ILDs are being developed to replace SiO

. These changes are leading to

post-metal anneals as low as 300°C. In multilevel metallization schemes,

such anneals are repeated every time a new layer of metal interconnects is

created. Thus, the first APDB layer at the contact level may experience

several of these anneals plus those (around 300 to 450°C for about

30 minutes) used during packaging of these chips. It is safe to say that

concerns related to the stability of the APDB and metal layers at the

process temperatures are becoming fewer.

The temperature rise during the device or circuit in use is increasing

with the continued miniaturization of the devices and circuits. However,

the operating device/circuit temperature is still expected to be lower than

the process temperature. Now we are concerned with the combined effect

of applied field and temperature on the stability of the APDB used.

Because lower temperatures will reduce the impact of increasing electric

fields, an efficient way to dissipate heat away from the active circuits is

becoming a major challenge.

Electric Field

The final applicability of the APDB films will be determined by the

stability of the electrical properties of the devices/circuits in which such

films are used. In most cases, the metallurgical stability, first determined

by the experiments that perform diffusion analyses and identify phase

changes, is found to determine the effectiveness of the APDB. These obser-

vations, however, do not guarantee the electrical stability when the films

Ch_05.qxd 11/29/04 6:20 PM Page 259

are subjected to high electric fields and current densities. It is thus neces-

sary to determine the two stabilities independently, especially now when

new materials such as Cu and low-k ILD are being introduced and film

thickness, particularly that of the APDB, is being reduced.

When using the APDB films on semiconductors, such as during the

formation of contacts, the electrical stability of a p-n junction and/or the

Schottky-type contacts is examined as a function of the annealing tem-

perature, time, and ambient. Changes from the idealized (or control) current-

voltage (I-V) behavior are noted and analyzed to determine the stability

and reliability under the actual fabrication and use conditions.

When the APDB layers are formed between the dielectric (ILD) and

the interconnections (Cu or Al), their electrical stability has to be fully

determined. This is done by examining their capacitance-voltage (C-V),

current-voltage (I-V), capacitance-time (C-t), and current-time (I-t) char-

acteristics. Furthermore, triangular voltage sweep characteristics, charge

and voltage-to-breakdown, in-plane and out-of-plane k, and dielectric-

loss measurements of a metal-insulator semiconductor and/or a metal-

insulator-metal capacitor need to be measured. Bias-temperature stressing

(BTS) during C-V and I-V measurements determines the electrical stabil-

ity under simulated use conditions. Exposure to invading environments

(high humidity and temperature) during such tests challenges the reliabil-

ity. The I-V measurements illustrate the dielectric strength, charge trap-

ping, and conduction mechanisms. Any metallic penetration, in general,

will change these characteristics and thus determine the usefulness of the

APDB used.

5.4 Diffusion Barrier Materials

Many investigations of diffusion barrier materials have been carried

out over the past four decades. This section reviews materials used as the

APDBs between silicon or silicide and Al, and between SiO

and Cu.

5.4.1 Metal Nitrides, Carbides, and Borides as

APDB Used with Al

Table 5.1 summarizes the reported effectiveness of various refractory

metal nitrides, carbides, and borides as APDB materials between Si or

silicide and Al. All the refractory materials have very high melting points

and are effective barriers up to at least 500°C. They all qualify, therefore,

for silicon integrated circuit applications in the thicknesses used in these

qualifying experiments (in the range of approximately 40 to 200 nm).

260 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_05.qxd 11/29/04 6:20 PM Page 260

DIFFUSION BARRIERS IN SEMICONDUCTOR DEVICES, MURARKA 261

Besides high melting point, what makes these nitrides, carbides, and

borides so effective as an APDB? These films are generally deposited by

reactive sputtering at or near room temperature and thus have a very small

grain size and a high density of fast diffusion paths. Deposited films are,

in general, in a state of compressive stress, possibly as a result of a small

excess of nitrogen, carbon, boron, and/or oxygen. This excess of nitrogen,

Table 5.1. High-Melting Diffusion Barriers Between a Substrate and Al

Metallization: Nitrides, Carbides, and Borides

Barrier Temperature

Intermetallics

Material Substrate (°C) Detected References

TiN Si 550 a

TiSi

550 a, b, c

PtSi 600 AlN, Al

Ti d, e, f

CoSi

550 d

NiSi 500 g

ZrN Si 550 Al

HfN Si 500 i

TaN NiSi 600 AlN, Al

Ta e

Ta N Pd Si 550 j

CoSi

550 j

TiC Si 500 k

PtSi 600 Al

, Al

Ti f

TiSi

500 k, l

CoSi

500 Co

ZrB Si 600 m

Temperature at which the reaction is first observed.

a. C. Y. Ting, J. Vac. Sci. Technol., 21:14 (1982)

b. N. Cheung, H. Von Seefeld, and M.-A. Nicolet, Proc. Symp. on Thin Film Interfaces and

Interactions (J. E. E. Baglin and J. M. Poate, eds.), Electrochem Soc., Princeton, NJ (1980),

p. 323

c. C.-Y. Ting and M. Wittmer, Thin Solid Films, 96:327 (1982)

d. R. J. Schutz, Thin Solid Films, 104:89 (1983)

e. M. Wittmer, Appl. Phys. Lett., 37:540 (1980)

f. M. Wittmer, J. Appl. Phys., 53:1007 (1982)

g. M. Finetti, I. Suni, and M.-A. Nicolet, J. Electron. Mater., 13:327 (1984)

h. L. Krusin-Elbaum, M. Wittmer, C.-Y. Ting, and J. J. Cuomo, Thin Solid Films, 104:81 (1983)

i. I. Suni, M. Maenpaa, and M.-A. Nicolet, J. Electrochem. Soc., 130:1215 (1983)

j. M. A. Farooq, S. P. Murarka, C. C. Chang, and F. A. Baiocchi, J. Appl. Phys., 65:3017 (1989)

k. M. Eizenberg, S. P. Murarka, and P. A. Heimann, J. Appl. Phys., 54:3195 (1983)

l. A. Applebaum and S. P. Murarka, J. Vac. Sci. Technol., A4:637 (1986)

m. J. R. Shappiro, J. J. Finnegan, and R. A. Lux, J. Vac. Sci. Technol., B4:1409 (1986)

Ch_05.qxd 11/29/04 6:20 PM Page 261