Хаимов 3.С. Основы высшей геодезии

Подождите немного. Документ загружается.

в 2

Вг

6, и

+ /,

Л2

180

(5.63)

Однако при решении прямой задачи нам даются только Ви

Lu А\ и 5, поэтому средние значения широт и азимутов оста

ются неизвестными. Неизвестны также разности &, / и t, необ

ходимые для вычисления поправочных членов. Вследствие этого

решение прямой задачи со средними аргументами по формулам

Гаусса может быть выполнено только способом последователь

ных приближений, причем принимается в качестве первого при

ближения Bm = Bi и Ат — А\ или же их определяют прибли

женно, например, по карте.

При решении задачи на большие расстояния в формулах

(5.60) удерживаются дополнительные поправочные члены. Од

нако решение прямой задачи на малые расстояния — от 40 до

120 км — целесообразнее производить по способу вспомогатель

ной точки или численными методами; на расстояния же от 120

до 400 км наиболее удобны полные формулы со средними аргу

ментами [5], а также численные методы.

Обратная геодезическая задача

При решении обратной задачи для расстояний до 400 км наи

более удобными оказываются формулы со средними аргумен

тами Гаусса. В этом случае задаются координаты Ви Lx и В2,

Ь2 двух точек, требуется определить А\, Л2, s.

Так как координаты точек известны, сразу определяются

разности Ь = В2—В\ и l = L2—Li, а также широта

Вт — (В1-\-В2)12. (5.64)

Тем самым основной недостаток решения прямой задачи,

связанный с необходимостью применения метода последователь

ных приближений, в данном случае исключается. Из формул

решения прямой задачи (5.62) получим

SCosA - b I Y -

2<2

+ (<sin^ ) a l - о

Л т ~ ( 1 ) Л 24р* \ Q'

s sin Am — 1 c-g --ffl- Г1 + = P, (5-65)

\Л)т L -ь4р J

< -Ы п В „ Г

+ +

L 24p J

где (l)m = PlMm, (2)m = p/Nm. После чего определим

tg Am = PlQ, (5.66) s = P/sin Am = Q/cos Am. (5.67)

По знакам числителя и знаменателя (5.66) определяют чет

верть, к которой относится средний азимут Ат.

Аг = Am — tl2 (5.68) и Л

= Ат ± 180° + №. (5.69)

Приведенные формулы позволяют вычислить широту и дол

готу с точностью до

0 0 0 1

—

0 0 0 2

" и азимут — до

0 0 1

" для

расстояний до 40 км. При расстояниях до 400 км в формулах

удерживают дополнительные поправочные члены. Для больших

расстояний применяют прямые способы решения главной геоде

зической задачи [5].

При использовании ЭВМ указанные формулы преобразуют

к виду, удобному для счета на машинах [13].

§ 26 РЕШЕНИЕ ГЛАВНОЙ ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ

ПО СПОСОБУ БЕССЕЛЯ

Способ Бесселя — наиболее универсальный способ решения

главной геодезической задачи прямым методом. Он позволяет

получать решение на различные расстояния с любой заданной

точностью. В нем от геодезических элементов на эллипсоиде пе

реходят к соответствующим элементам на вспомогательной

сфере. При этом геодезическая линия изображается дугой боль

шого круга так, что азимуты в соответствующих точках обеих

линий равны, широты точек на сфере равны приведенным ши

ротам соответствующих точек на эллипсоиде. Затем осуществ

ляется решение полярного треугольника и определяются иско

мые величины на сфере, после чего они переносятся на эллип

соид.

Прямая геодезическая задача

На рис. 26 показаны соответствующие элементы на эллипсоиде

и сфере:

— длина геодезической линии, а — соответствующая

ей дуга большого круга на сфере, т — вспомогательная вели-

Рдс, 26, Решение главной задач# по способу Бесселя

чина, равная дуге большого круга, проведенной из точки по

люса Р' до встречи с продолжением дуги а под углом в 90°,

М — вторая вспомогательная величина, I и со — разности сфе

роидических и сферических долгот, Bt и U% — геодезическая и

приведенная широты. Решение проводится в следующем по

рядке:

1) переход на сферу под условием равенства азимутов линий

Q1Q2 и Q /Q 2/ в соответствующих точках. Для этого использу

ется основное уравнение геодезической линии (уравнение Клеро)

г sin А = const. (5.70)

Но r = a cos U = Ncos В, поэтому уравнение (5.70) для точек Qi

и Q2 будет иметь вид

cos Uх sin Л ^ cos U2 sin Л2,

N{ cos B{ sin A j = N2 cos B2 sin A2. (5-71)

Эти формулы позволяют однозначно построить полярный тре

угольник на сфере радиуса а таким образом, что в каждой

точке дуги большого круга а азимуты будут равны азимутам

в соответствующих точках геодезической линии эллипсоида,

в том числе будут равны углы в точках Qi и Q/; Q2 и Q/. Для

этого надо от геодезических широт перейти к приведенным по

формуле

tg£/ = l/ T = i5tgB (5.72)

или по разности Вг— Uh которая для эллипсоида Красовского

будет

Bt — Ut = 346,314 sin 2Bt — 0,2907 sin 4Bt + 0,0003 sin 6Bt9 (5.73)

после чего определяют

Ut — Bi — (Bt — Ut); (5.74)

2) определение a no

и наоборот —

no a

o = as+psinacos(2Al + o)4-Ysin2acos(4M -l-2o)-f . . .,(5.75)

= —

[a— psincrcos(2M + a)

— у

sin 2acos (4M

2a)

. . .

(5.76)

Коэффициенты a, |3, у табулированы [5];

ctg M = cos AJtg Ult (5.77)

Определение a по

по формуле (5.75) осуществляется спо

собом последовательных приближений. В первом приближении

принимают

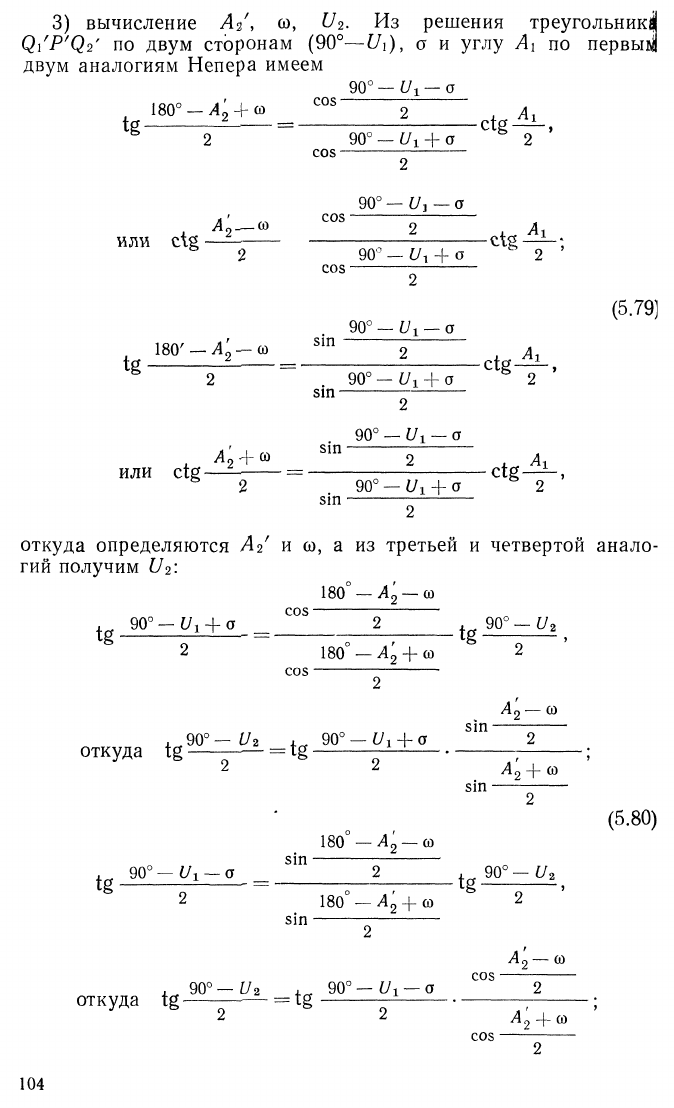
3) вычисление А /, ю, U2. Из решения треугольник!

Qi'P'Qy по двум сторонам (90°—£Л), о и углу Ах по первым

двум аналогиям Непера имеем

90° — и г — а

ctg 4 l

- Ux + a

ииг>

А 2 — со

90°

— U j— G

И ctg

COS

90° U x -f- о

COS

-А 2 — со

90°-— U \ — cx

180'-

sin

■ctg A .

(5.79)

------------

------

= -----------------------------ctg—-

2 . 9 0 °— Ux + o 2

-------------------

Л 2

+ <° 8Ш

или ctg—

------

-----------

-----------------ctg—2-,

s 2 90 — Ui-\-o 2

sin

-------------------------

откуда определяются А*' и со, а из третьей и четвертой анало

гий получим U

180° — a L — со

cos ■

90° — U1 — а

90 ° - Ц 1 + о

______________

2 . 90° — U 2

180°-Л; + (о

cos

-------------------

А2 — со

90° — U2 ^ 90° — Ux-\~ о Sm 2

откуда tg

-----

= tg

--------------------------------

-------

2 z А2 + со

sin

--------------

sin -

180 — А 2 — со

(5.80)

t 90° — U\ — а =

____________

__________t 90° — U 2

2 1 8 0 ° -Л 2 + со 2

sin

----------

--------------

cos

А2 — (о

. 90° - U 2 , „ 90° — U г — а 2

откуда tg

-------------

= tg

----------

-------------

А 2 "~j~ 0)

cos

---------------

4) вычисление разности долгот I по вычисленному значе

нию со:

/ = со — sin т [ a -f sin о cos (

М -f о)], (5.81)

где ш и Pi табулированы,

sin т == sin Ах cos Ux\ (5.82)

5) вычисление геодезической широты В2 по U2:

B2 — U2 = 346,3143 sin 2U2 + 0,2907 sin W 2 + 0,0003 sin

t/a# (5.83)

= t

/ 2

+ (B

- t / a). (5.84)

На этом завершается решение прямой геодезической задачи.

Обратная геодезическая задача

Порядок решения:

) определение разности долгот

l = L2—Li; (5.85)

) вычисление приведенных широт по геодезическим по фор

муле (5.74);

3) вычисление разности сферических долгот со по разности

геодезических долгот / по формуле (5.81). Поскольку величины

т , о,

М неизвестны, применяют способ последовательных при

ближений, принимая в первом приближении со = /, и затем, оп

ределив азимуты из аналогий Непера для треугольника Q / P ^ 1:

»— г - 1 - * ^ tgf

sin -

и2 + иг

И tg—

-----

— — — ^tg =

----------

-------

tg — ,

и2—их ъ

C° s

-------

вычисляют m, M и а по формулам (5.82), (5.77) и (5.75).

Второе приближение для со получают из формулы (5.81), за

тем вновь вычисляют A I, А2, m, М и а до тех пор, пока резуль

таты не будут иметь заданной точности;

4) вычисление s по а по формуле (5.76).

Существует много видов представления формулы Бесселя

в зависимости от расстояния и требуемой точности [15].

В связи с переходом к уравниванию триангуляции всех клас

сов на плоскости наибольшее применение получило решение об

ратной задачи иа большие расстояния. Прямая же задача ис

пользуется только для контроля.

§ 27. РЕШЕНИЕ ПРЯМОЙ ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ

ПО МЕТОДУ РУНГЕ—КУТТА— ИНГЛАНДА И ГЛАВНОЙ

ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ НА ШАРЕ

В конце прошлого и начале нынешнего века немецкие ученые

Рунге и Кутт разработали численный метод интегрирования

дифференциальных уравнений первого порядка. Благодаря своим

достоинствам и удобству программирования этот метод полу

чил широкое распространение в связи с использованием ЭВМ.

В дальнейшем этот метод был модифицирован, появились фор

мулы, ускорявшие решение задачи. Наиболее экономичным

среди них является метод Рунге—Кутта—Ингланда, который

выгодно применять для решения прямой геодезической задачи

на расстояния порядка 300 км. В средних широтах он позво

ляет определять координаты с ошибкой, не превышающей

—

15 см, и азимуты менее 0,003".

Применяя этот метод для численного интегрирования трех

дифференциальных уравнений (5.28) при решении прямой гео

дезической задачи, получим

В2 = Bi -f- (ABi -f- 4ДВз -f- AB

;

= L, + (A + 4AL

+ AL

; (5.86)

= A\ + (АЛХ + 4ДЛ

-f~ А Л

)

где

A Bi = s0V3i cos a*, A At = s0Vi sin a*/cos cp*, A A t = A Li sin <p*;

V, =

+ 0,75e

' 2

cos

q>,)/(l + 0,25e'2 cos

q>*), t = 1,2,3,4, s

= sic.

(5.87)

Для эллипсоида Красовского: c = 6 399 698,9 м; 0,25б' ==

= 0,001 684 631.

Значения аг и срг определяют в зависимости от номера при

ближения i:

i а Ф

1-е Лх Вг

2-е Ах + 0,5 A At Вг + 0,5 А Вг

3-е Аг + 0 ,2 5 (А Аг + А А2) Bt + 0,25 (А + Вг А В2)

4-е Ai — А А2 -f- 2 А А3 В^ — А В2 2 Д В$

Этот метод позволяет решать задачи на любые расстояния.

При больших длинах сторон их делят на части и затем после

довательно вычисляют каждую часть линии по указанным фор

мулам. Следует иметь в виду, что в таких случаях увеличива

ются ошибки определяемых величин и объем вычислений.

Решение главной геодезической задачи на шаре

Часто в приближенных расчетах, особенно в картографических

целях, Землю принимают за шар радиуса, равного среднему

радиусу земного эллипсоида на широте BQ: jR

= ]/7W

A/r0. Тогда

вследствие близости поверхности земного эллипсоида к шаро

вой их практически молено не различать в пределах пояса ши

риной 300—400 км даже в точных работах, так как в пределах

1,5° к северу и югу от параллели с широтой Во все линии, углы

и сферические координаты будут равны соответствующим ли

ниям, углам и координатам на эллипсоиде. При больших рас

стояниях разница между ними будет быстро возрастать. Но для

многих практических задач, особенно при использовании карт

мелкого масштаба, ошибки в определении координат и длин

линий в несколько десятков километров часто бывают вполне

приемлемыми. Решение же главной геодезической задачи в та

ких случаях значительно упрощается и сводится к простому ре

шению полярного сферического треугольника по двум сторонам

и углу между ними.

Прямая геодезическая задача. Заданы сферические коорди

наты точки Q'i (см. рис. 26) — широта Uь долгота азимут Ах

линии Q'iQr2 и ее длина ст. Требуется определить сферические

координаты точки Q'2, U2j X

= Xi + co и обратный азимут А2 =

— 180°+Л/2.

Из решения сферического треугольника Q'\P'Q'2 по теореме

косинусов и формулам котангенсов имеем

sin t

/ 2

= coscr sin t/i + sincrcos Ut cosAb

ctg со = ctg g cos U-l cosec Ax— ctg Аг sin Ul9 (5.88)

ctg A2 = ctg A\ cos a — tg и г sin a cosec Ax.

По этим формулам задача решается полностью.

Обратная геодезическая задача. Заданы сферические коор

динаты Uu U2, со точек и Q'2. Требуется определить ст, Аи А2.

Из решения того же сферического треугольника имеем

cos о = sin и г sin U2 + cos Ut cos U2 cos со,

ctg Ax = tg U2 cos и х cosec со— ctg со sin Ut (5.89)

ctg A

= ctgco sin U2— tg t^cos U2 cosec (0.

§ 28. ПЕРЕХОД ОТ ОДНОЙ СИСТЕМЫ ГЕОДЕЗИЧЕСКИХ

КООРДИНАТ К ДРУГОЙ С ПРИМЕНЕНИЕМ

ДИФФЕРЕНЦИАЛЬНЫХ ФОРМУЛ ПЕРВОГО И ВТОРОГО РОДА

Применение дифференциальных формул связано с решением за

дач по перевычислению геодезических координат на поверхно

сти земного эллипсоида. В геодезии эта задача возникает при

изменении исходной системы координат и уточнении размеров

земного эллипсоида. Самостоятельное значение она имеет в кар

тографии при сравнении координат, вычисленных на разных эл

липсоидах, и использовании картографических материалов, от

несенных к ним.

Такая задача возникла перед советскими геодезистами

в связи с переходом от эллипсоида Бесселя к эллипсоиду Кра-

совского и была успешно решена ими в 1942— 1946 гг. Прм|

уточнении исходных геодезических данных также возникает за-i

дача о перерасчете всех координат данной сети и координат уг

лов рамок съемочных трапеций.

Дифференциальные формулы позволяют сократить тот огром

ный вычислительный труд, который требуется при подобном пе

ревычислении ранее уравненных координат всех опорных геоде

зических пунктов. Это оказывается возможным потому, что пов

торное вычисление координат заменяется вычислением неболь

ших поправок к уже имеющимся координатам пунктов. Фор

мулы для вычисления таких поправок значительно проще гро

моздких формул прямой и обратной геодезических задач; реше

ние может осуществляться при помощи четырех- и пятизначных

таблиц натуральных тригонометрических функций, а не восьми

десятизначных, как при новом вычислении координат. Такими

формулами для вычисления поправок в координаты и азимуты

направлений и являются дифференциальные формулы первого

и второго рода.

Дифференциальные формулы первого рода служат для вы

числения поправок в координаты пунктов и азимуты направле

ний в случае изменения исходных данных (широт, долгот, ази

мутов или длин базисов), на основе которых развивалась геоде

зическая сеть.

Дифференциальные формулы второго рода применяются при

вычислении поправок в координаты пунктов, высоты и азимуты

направлений в случае изменения параметров референц-эллип-

соида (большой полуоси или сжатия) или изменения его ориен

тировки относительно принятых координатных осей, а также

при перевычислении координат с одного эллипсоида на другой.

Дифференциальные формулы первого рода

Сущность задачи, решаемой при помощи дифференциальных

формул первого рода, заключается в следующем. Имеем два

пункта Q

и Q

(рис. 27) с из

вестными координатами, ази

мутами направлений QiQ

и расстоянием между

ними, т. е. известны В\, Ьи Аи

£>2, L2, А2 и s Необходимо оп

ределить поправки в коорди

наты пункта

Q2—dB2, DL2 и

в азимут dA2, если коорди

наты пункта Qu азимут Aitts

изменились на небольшие ве

личины — dB\, dLu dAu ds.

(Bj+dBjLj+dLj)

Очевидно, что координаты

пункта Q

и азимут направле

ния Q2Q

также изменятся на

небольшую величину:

Рис. 27 Влияние изменений исход

ных данных на координаты опреде

ляемого пункта

В'2 — В%-\-dBz, Ll2 — L2~\~dL2> Ar2==A2~\- dA2y

где dB2i dL2i dA2 выражены в функции от dBu dLu dAu ds.

В полных курсах высшей геодезии [5] доказывается, что

dB2 = dB±

-----

— cos BmdA-i + b ;

p s

dL2 = dL1 + — tg BmdB1 + — sec BmdAt + 1 — ; (5.90)

P P 5

dA2 = dA1-\~ — secBmdS

| — igBmdAx {-/ — ,

p p s

где (Bl + B2)/2.

Эти формулы позволяют для расстояний до 40 км получать

поправки с точностью в 0,002—0,003" Для больших расстояний

формулы принимают более сложный вид.

Дифференциальные формулы второго рода

Задача, решаемая в этом случае, заключается в вычислении по

правок в координаты и азимут направления с пункта Q

, свя

занного с исходным пунктом Q

, если изменились параметры

эллипсоида, при условии, что координаты исходного пункта и

азимут Q

с него не меняются. Изменение размеров референц-

эллипсоида ведет к изменению разности координат и азимутов

между расположенными на нем пунктами, поэтому вместо оп

ределения поправок dB2, dL2) dA2 можно найти поправки в раз

ности координат и азимутов b, I, t — db, dl, dt, т. e. полагать,

что новые координаты пункта будут

B'2 = Bx + b + db\ L'2 = Lx + l + dl, A' = Ax ± 180° + t + dt. (5.91)

Таким образом, достаточно найти дифференциальные по

правки db, dl, dt в функции изменения размеров эллипсоида

da = a\—а, de2 = e2

—е2, или da = a\—а, где ai, еи щ и а, е, а —

соответственно большая полуось, первый эксцентриситет и сжа

тие нового и старого эллипсоидов. Для расстояний до 40 км и

точности вычислений порядка

0 0 1

—

0 0 2

" эти поправки будут

db = — b

[ - ^ - - ( 1

-----

sin

Bm)de2J =

= — b - — (2—-3 sin

Bm) d a j;

d l= — l + ^ -s in

Bm de2j = — I [JjL + sin

Bmda] ■ (5.92)

dt — — -f -y- sin

Bmde2J = — t

- sin

Bmd a j.

Помимо исправления координат дифференциальные фор

мулы второго рода применяются в градусных измерениях, при

установлении исходных геодезических дат и при уравнивании

астрономо-геодезической сети страны.

Однако при перевычислении координат на новый эллипсоид

приходится применять дифференциальные формулы как вто

рого, так и первого рода в связи с тем, что в результате пере

вычисления меняются координаты исходного пункта в каждой

паре смежных пунктов. В этом случае применяются более слож

ные формулы, учитывающие совместное влияние дифференци

альных поправок первого и второго рода [5].

Более сложный вид имеют дифференциальные формулы вто

рого рода, учитывающие дифференциальные поправки коорди

нат из-за изменения параметров и ориентировки земного эллип

соида [13], [14].

Глава

ПЛОСКИЕ ПРЯМОУГОЛЬНЫЕ

КООРДИНАТЫ ГАУССА—КРЮГЕРА

§ 29 ОБЩИЕ СВЕДЕНИЯ

Система плоских прямоугольных координат в проекции Га

усса — Крюгера, или просто — координаты Гаусса — Крюгера,

была введена в нашей стране постановлением III Геодезиче

ского совещания при Геодезическом комитете Госплана СССР

в 1928 г., но всеобщее распространение в геодезических работах

получила после выпуска в 1930 г. Таблиц для вычисления ко

ординат Гаусса — Крюгера, составленных В. И. Звоновым и

Д. А. Лариным под редакцией и при участии Ф. Н. Красов

ского.

Распространение системы координат Гаусса — Крюгера, вы

теснивших все применявшиеся ранее, привело к установлению

определенного порядка в использовании результатов геодези

ческих измерений и к унификации их обработки.

Необходимость введения системы плоских координат вызы

валась тем, что эллипсоидальная геодезическая система, будучи

наиболее общей и удобной при изучении научных проблем выс

шей геодезии, изображении всей Земли на картах и решении

геодезических задач на значительные расстояния, становится

сложной и мало пригодной в массовых геодезических работах

по созданию съемочного обоснования топографических карт и

различных инженерных сооружений. Координаты этой системы

(широта и долгота) выражаются в угловых единицах, линейное

значение которых меняется вместе с широтой места; направле

ния меридианов, от которых отсчитываются азимуты, непарал

лельны и необходим специальный учет этой непараллельности;

формулы, служащие для решения различных геодезических

задач, чрезвычайно сложны и громоздки.