Хант Р.В.Г. Цветовоспроизведение

Подождите немного. Документ загружается.

паразитными хроматическими контурами. SECAMсистема лишена этого недостатка

благодаря частотной модуляции хроматических сигналов.

PALсистему можно модернизировать по данному параметру за счет применения

т.н. узкополосного режекторного фильтра, который задерживает в основном яркост

ный сигнал на частотах, лежащих возле частот хроматической поднесущей. Паразит

ные краевые эффекты в данном случае возникают лишь при очень жесткой работе это

го фильтра, поэтому наилучшего результата можно добиться на промежуточных ее

уровнях.

22.15.3 Издержки всех трех систем

В любой из трех обсуждаемых систем на мелких паттернах могут возникнуть пара

зитные визуальные эффекты, проявляющие себя:

551

ГЛАВА 22 NTSC, PAL И SECAM

1.5

1.0

0.5

0.5

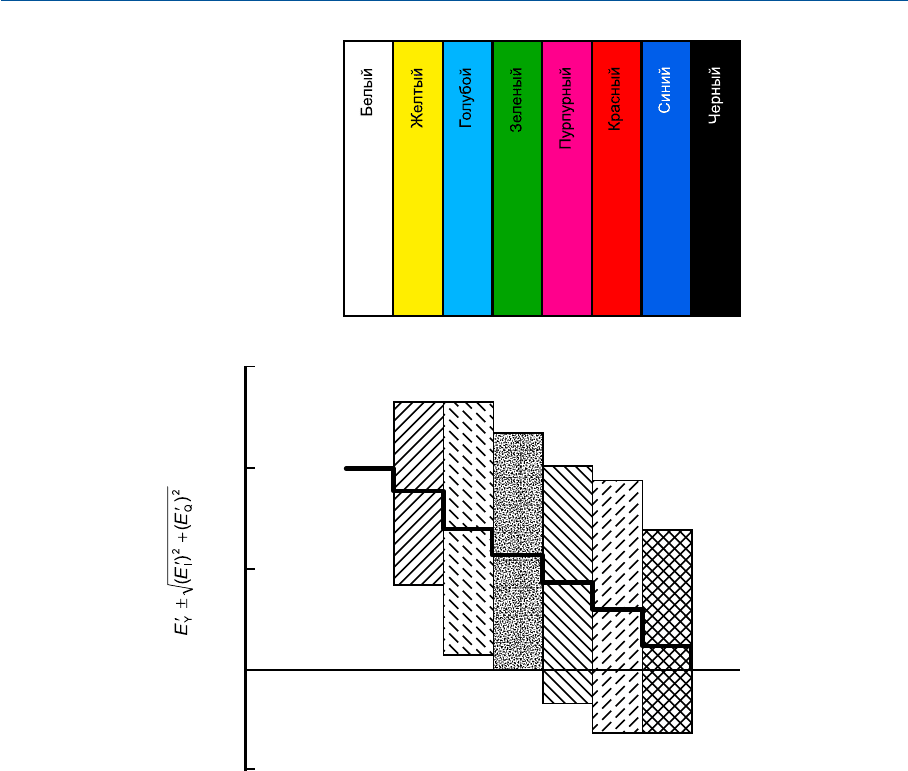
Рис. 22.11 В верхней части рисунка показан типичный тестобъект. В нижней части дан ха

рактер колебаний амплитуды передаваемого сигнала вдоль единичной строки. Жирная черная

линия — амплитуда яркостного сигнала; прямоугольники с заливкой — диапазоны амплитуд

объединенных яркостного и хроматических сигналов. Ось ординат NTSCсистемы, но с тем же

успехом она подходит и системе PAL.

— в NTSCсистеме в виде «пилы», появляющейся только на монохромных диспле

ях (цветные вообще не подвержены этому дефекту);

— на монохромных дисплеях PALсистемы в виде паразитных линий, повернутых

на 30° от горизонтали (в гораздо меньшей степени на цветных);

— в SECAMсистеме в виде «шеврона» («елочка»), появляющегося на экранах

только монохромных приемников.

Высокое технологическое сходство между NTSC и PALсистемами обеспечивает

их высокую совместимость. SECAMже стоит особняком. PALсистема, в которой

сдвиг фаз выражен гораздо меньше, чем в NTSC, позволяет передавать сигнал на го

раздо бо\льшие расстояния по коаксиальным кабелям. При этом NTSCсистему можно

использовать в локальном вещании без усложнения конструкции приемника схемой

задержки.

552

ГЛАВА 22 NTSC, PAL И SECAM

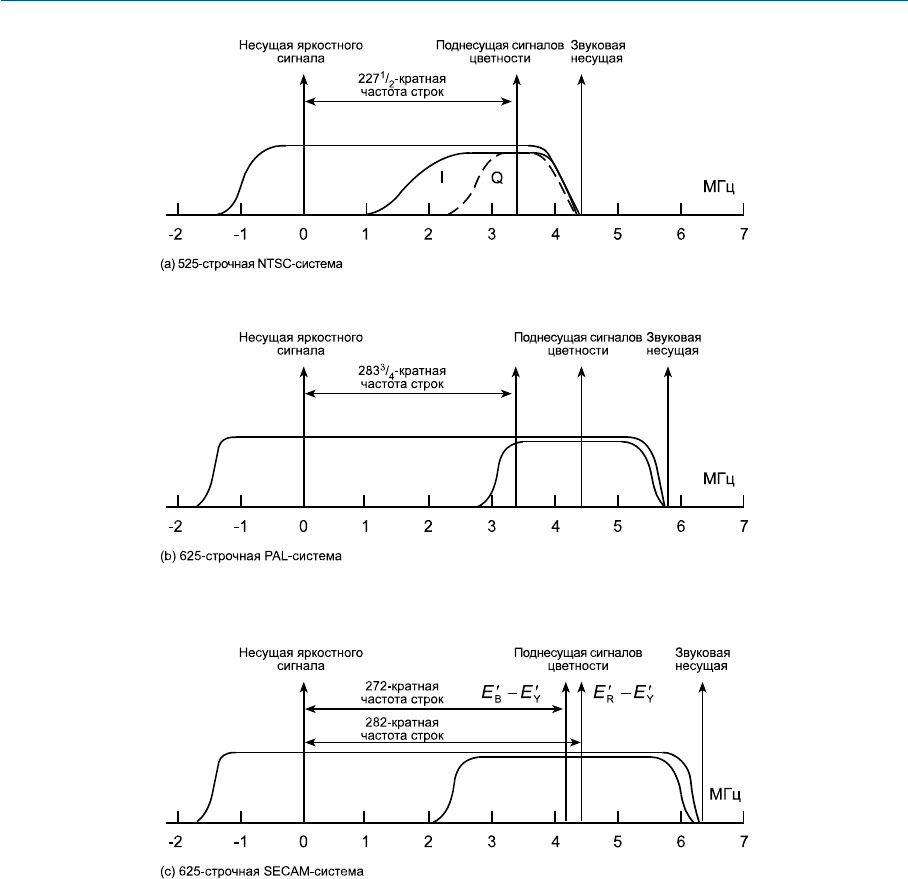
Рис. 22.12 Распределение частот: (а) — в 525строчной системе NTSC; (b) — в 625строчной

PALсистеме; (с) — в 625строчной системе SECAM.

Возможно, наиболее важным отличим SECAMсистемы от двух других является

то, что только в ней не возникает конфликта между яркостным сигналом и сигналами

цветоразностными, но в целом, SECAM — это наиболее сложная система.

PAL благодаря автоматической фазовой коррекции устойчивей в отношении по

грешностей по цветовому тону воспроизводимых стимулов, нежели система NTSC, в

которой необходимость управления цветовым тоном на стадии приема требует доста

точно высокой квалификации пользователей.

И последнее в этом разделе: PAL и SECAM обычно используют 625строчные телеви

зионные стандарты, в то время как NTSC обычно пользуется стандартами

525строчными (в результате чего изображения, воспроизводимые последней, имеют

меньшее разрешение и визуальную резкость). С другой стороны, поскольку в

525строчных системах частота полукадров обычно равна 60 Гц мелькание оказывается

не столь заметным как в 50герцовых системах при 625строках развертки.

553

ГЛАВА 22 NTSC, PAL И SECAM

ТАБЛИЦА 22.4 Частоты различных телевизионных систем

Система NTSC PAL SECAM

Количество строк 525 625 625

Частота полных кадров/с 29.97 25 25

Примерная ширина полосы на полное

изображение (МГц)

Превышение частоты хроматической

поднесущей над яркостной несущей (МГц)

3.579545 4.43361875 4.440625

4.250

Частота хроматической несущей как

произведение на частоту строк

227.5 283.75 282

272

Тип модуляции хроматических сигналов Амплитудная Амплитудная Частотная

Превышение частоты звуковой несущей над

яркостной несущей (МГц)

4.5 6.0 6.5

Ширина полосы

(на 3 дБ ниже максимума) 1.0 — —

Ширина полосы

(на 3 дБ ниже максимума) 0.3 — —

Ширина полосы

(на 3 дБ ниже

максимума)

— 1.3 1.5

Ширина полосы

(на 3 дБ ниже

максимума)

— 1.3 1.5

Превышение частоты несущей яркостного

сигнала над минимальной шириной полосы

1.25 2 2

Примерная общая ширина полосы вещания

(МГц)

6 8 8.5

22.16 НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ ГРАФИЧЕСКИЕ

ПОСТРОЕНИЯ

Если обратиться к рис. 22.13, то станет понятно, что стимул «М» (чья цветность ле

жит на линии, соединяющей позиции кардинальных стимулов G и B) можно уравнять

подходящей смесью этих стимулов, и поэтому мы можем записать:

MGB() () ()MGBº+

Аналогично стимул N, цветность которого лежит на линии, соединяющей позиции

стимула М и кардинального стимула R, можно уравнять подходящей смесью послед

них:

NMR() () ()NMRº+

Точная позиция точки, представляющей стимул N на линии, соединяющей пози

ции кардинального стимула R и стимула M, определяется законом центра тяжести и

будет той же, что и у центра тяжести весов:

mG nB

, «давящего» на (М) и

, «давящего» на (R)

Сходный результат получим, используя веса:

mE nE

Однако

mE nE E lE

GBYR

+=-

, следовательно:

ElE

Если точки М и R лежат на линии постоянной

(то есть,

), то отношения ве

сов сводятся к:

ElE

Расстояние от точки, представляющей цветность стимула N, до точки М можно вы

числить из:

ElE lE

YR R

()-+

где

— это длина линии, соединяющей точки R и М.

Поскольку l и

— константы, расстояние NM будет пропорционально

,и,

следовательно линия, соединяющая R и M, может образовать линейную шкалу

. Последнюю легко конвертировать в линейную шкалу

()EEE

RYY

, отняв 1.0

от каждого значения. Для удобства можно использовать любую линию, параллельную

554

ГЛАВА 22 NTSC, PAL И SECAM

RM, в частности, такую как РТ на рис. 22.13 (с точкой Р, лежащей на отрезке BG).

Если линия, идущая от C

через S

, пересекает ее в точке S, а позиция линии РТ выбра

на так, что PS = 1.0 на специальной шкале, то прочие значения найти будет очень лег

ко.

Отметим, что приведенная схема потому дает корректные результаты, что в точке

сигнал

, и, следовательно, линия, проходящая через S

— это линия, для ко

торой

=10.

(следовательно

()EEE

RYY

-=0

), а линия, идущая от СВ и проходя

щая через В и G — это линия, для которой

, и, таким образом

(следова

тельно,

() .EEE

RYY

-=-10

В принципе, сходное построение можно использовать для получения веера линий,

исходящих из C

. В этом случае расстояния будут равными:

где l

— это длина линии, идущей от точки В параллельно

оси, и которая пересекает

линию GR в точке М. К сожалению, геометрия

¢¢

диаграммы такова, что данный ме

тод не практичен для шкалирования

, но в отношении ряда других диаграмм

цветности он вполне применим.

555

ГЛАВА 22 NTSC, PAL И SECAM

PS T

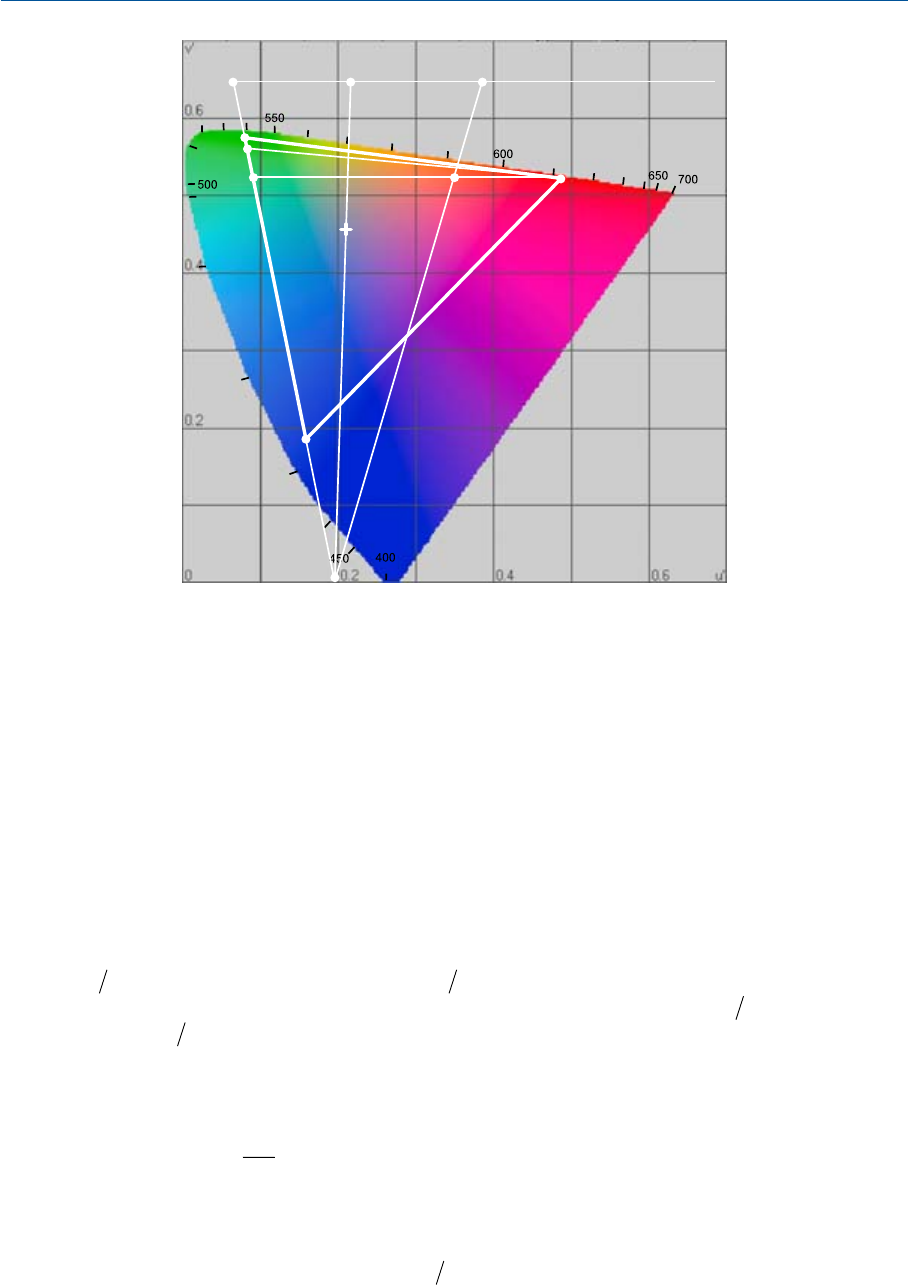
Рис. 22.13 Поскольку линия, соединяющая точки RиM—этолиния постоянной величины

смесь стимулов позиций R и M будет представлена точками с центрами тяжести весов прямо

пропорциональными фотометрической яркости стимулов R и M. Следовательно, долю стимула

R в смеси можно представить в виде равномерной шкалы на отрезке MR или на любой другой

линии, параллельной отрезку MR, в частности линии PT. Таким образом, равномерную шкалу

отрезка РТ можно использовать для поиска величин R/L и, следовательно,

()/RL L-

для линий

постоянного отношения R/L, идущих из C

ТАБЛИЦА 22.5 Телевизионные стандарты разных стран

СТРАНА СИСТЕМА

Австралия PAL

Австрия PAL

Азербайджан PAL

Азорские острова PAL

Албания PAL

Алжир PAL

Аляска (штат США) NTSC

Ангилья —

Ангола PAL

Андорра —

Антарктида NTSC

Антигуаи Барбуда NTSC

Аргентина PAL

Армения SECAM

Аруба NTSC

Атолл Мидуэй —

Афганистан PAL

Багамы NTSC

Бангладеш PAL

Барбадос NTSC

Бахрейн PAL

Белиз NTSC

Белоруссия SECAM

Бельгия PAL

Бенин SECAM

Бермуды NTSC

Болгария PAL

Боливия NTSC

Босния—Герцеговина PAL

Ботсвана PAL

Бразилия PAL

Британский Индийский океан NTSC

Бруней Даруссалам PAL

БуркинаФасо SECAM

Бурунди SECAM

Бутан —

Вануату —

Ватикан —

Великобритания PAL

Венгрия PAL

Венесуэла NTSC

ВоллисиФутуна SECAM

Восточный Тимор PAL

Вьетнам NTSC и SECAM

Габон SECAM

Гавайи (штат США) NTSC

Гаити NTSC

СТРАНА СИСТЕМА

Гайана NTSC

Гамбия PAL

Гана PAL

Гватемала NTSC

Гвиана (французский язык) SECAM

Гвинея PAL

Гвинея—Бисау PAL

Германия PAL

Гибралтар PAL

Гондурас NTSC

Гонконг PAL

Гренада NTSC

Греция PAL

Грузия SECAM

Гуам NTSC

Дания PAL

Джибути SECAM

Доминиканская республика NTSC

Египет PAL

Замбия PAL

Западная Сахара —

Западный берег и Сектор Газа

(Палестина)

PAL

Зеленый мыс —

Зимбабве PAL

Израиль PAL

Индия PAL

Индонезия PAL

Иордания PAL

Ирак SECAM

Иран SECAM

Ирландия PAL

Исландия PAL

Испания PAL

Италия PAL

Йемен PAL и NTSC

Казахстан SECAM

Камбоджа PAL

Камерун PAL

Канада NTSC

Канарские острова PAL

Катар PAL

Кения PAL

Кипр PAL

Кирибати PAL

Китай PAL

Кокосовые острова —

556

ГЛАВА 22 NTSC, PAL И SECAM

СТРАНА СИСТЕМА

Колумбия NTSC

Коморские острова —

Конго SECAM

Корея Северная PAL и NTSC

Корея Южная NTSC

КостаРика NTSC

Котд’Ивуар SECAM

Куба NTSC

Кувейт PAL

Кыргызстан SECAM

Лаос PAL

Латвия PAL

Лесото PAL

Либерия PAL

Ливан SECAM

Ливия PAL

Литва PAL

Лихтенштейн —

Люксембург PAL и SECAM

Маврикий SECAM

Мавритания SECAM

Мадагаскар SECAM

Мадейра PAL

Майот SECAM

Макау PAL

Македония PAL

Малави PAL

Малайзия PAL

Мали SECAM

Мальдивы PAL

Мальта PAL

Марокко SECAM

Мартиника SECAM

Маршалловы острова NTSC

Мексика NTSC

Микронезия NTSC

Миянмар —

Мозамбик PAL

Молдова SECAM

Монако PAL и SECAM

Монголия SECAM

Монтсеррат NTSC

Намибия PAL

Науру PAL

Непал PAL

Нигер SECAM

Нигерия PAL

Нидерланды PAL

Никарагуа NTSC

Новая Зеландия PAL

СТРАНА СИСТЕМА

Новая Каледония SECAM

Норвегия PAL

О. Галапагос NTSC

О. Кайман —

О. Кука PAL

О. Самоа PAL

О. Вознесения —

О. Гваделупа SECAM

О. Гренландия PAL

О. Ниуэ PAL

О. Норфолк PAL

О. Пасхи PAL

О. Рождества —

Объединенные Арабские

Эмираты

PAL

Оман PAL

Пакистан PAL

Палау NTSC

Панама NTSC

Папуа — Новая Гвинея PAL

Парагвай PAL

Перу NTSC

Полинезия (французский

язык)

SECAM

Польша PAL

Португалия PAL

Пуэрто—Рико NTSC

Россия SECAM

Руанда —

Румыния PAL

Сальвадор NTSC

СанМарино PAL

Саудовская Аравия PAL и SECAM

О. св.Винсента NTSC

О. св.Елены —

О. св. Киттси Невис NTSC

О. св. Люция NTSC

О. св. ПирриМиквелон SECAM

Свазиленд PAL

Сейшельские острова PAL

Сенегал SECAM

Сербия и Черногория PAL

Сингапур PAL

Сиря PAL

Словакия PAL и SECAM

Словения PAL

Соединенные Штаты Америки NTSC

Соломоновы острова —

Сомали PAL

Судан PAL

557

ГЛАВА 22 NTSC, PAL И SECAM

558

ГЛАВА 22 NTSC, PAL И SECAM

СТРАНА СИСТЕМА

Суринам NTSC

СьерраЛеоне PAL

Таджикистан SECAM

Таиланд PAL

Tайвань NTSC

Танзания PAL

Того SECAM

Тонга NTSC

Тринидади Тобаго NTSC

Тристандакунья —

Тувалу —

Тунис SECAM

Туркии Кайкос —

Туркмения SECAM

Турция PAL

Уганда PAL

Узбекистан SECAM

Украина SECAM

Уругвай PAL

Фарое острова PAL

Фиджи NTSC

Филиппины NTSC

СТРАНА СИСТЕМА

Финляндия PAL

Фолклендские острова PAL

Франция SECAM

Хорватия PAL

Чад SECAM

Чешская республика PAL

Чили NTSC

Швейцария PAL

Швеция PAL

ШриЛанка PAL

Эквадор NTSC

Экваториальная Гвинея SECAM

Эритрея —

Эстония PAL

Эфиопия PAL

ЮжнаяАфрика PAL

Ямайка NTSC

Япония NTSC

Обсуждаемую методику можно использовать для получения контуров постоянных

: поскольку для линии, соединяющей R и М, расстояния равны:

то путем замены

мы получим:

0621 0956 10...++

Но для всех точек, лежащих на линии, соединяющей R и М, значение

постоянно

и равно

(

координата R), следовательно:

UV W

¢¢

VvUVW

()

¢¢

VvvUW()/1

Заменив в последнем уравнении переменные

на переменные I, L, Q, и при

своив переменной

значение 0.528, мы получим:

LILQ(.)/. . . .1 0 528 0 528 0 381 1168 0 683-=-++

Следовательно:

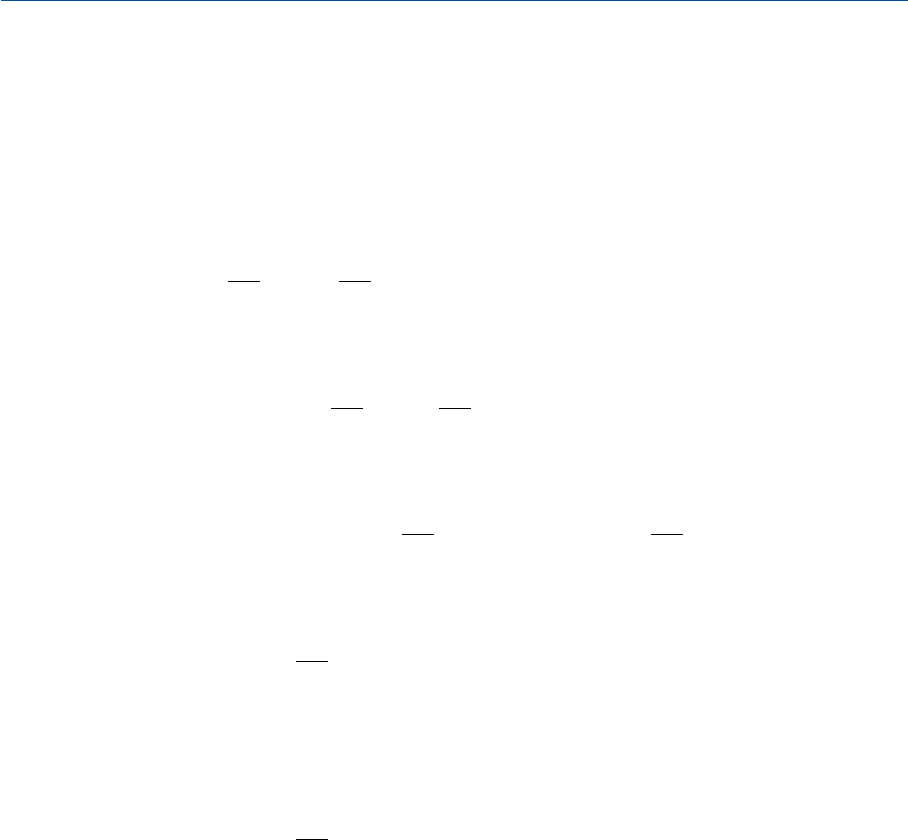
0894 0683 0381 1168....LQIL=-+

и, таким образом, получаем уравнение:

0894 0683 0381 1168....EEEE

YQIY

=-+

которое сокращается до:

=-0 557 0 400..

Но поскольку расстояния вычисляются по выражению:

0621 0956 10...++

то, заменив

, мы получим:

0621 0557 0621 0400 0956 10.. .. . .´-´++

Приняв, что l = 0.299, вышеприведенное выражение сокращается до:

0389 0255..

Таким образом отношение

будет линейным на протяжении участка RM (ну

левая отметка лежит на 22.5% от М). Аналогично, заменив

, мы получим рас

стояние для

0699 0504..

Таким образом, отношение

будет линейным на всем протяжении RM (нуле

вая отметка лежит на 50.4% от М).

И вновь для более удобного шкалирования вместо линии RM мы можем выбрать

линии параллельные ей (рис. 22.14). Линии, проходящие через S

во всех случаях со

ответствуют нулевой отметке, а линия, идущая от C

и проходящая через R (и для ко

торой

/.=199

) использована для позиционирования шкалы

; линия, выхо

дящая из C

и проходящая через G (и для которой

/.=-089

), использована для по

зиционирования шкалы

22.17 НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ УРАВНЕНИЯ

В данном разделе мы даем подборку уравнений, которые могут оказаться полезны

ми при выполнении разного рода вычислений для NTSC.

Уравнения связи фотометрической яркости воспроизводимого стимула с колоримет

рическими количествами кардинальных RGBстимулов:

559

ГЛАВА 22 NTSC, PAL И SECAM

EEEE

LRGB

YRGB

=++

0299 0587 0114

...

Уравнения перехода из RGBсистемы в систему XYZ и обратно:

10 0607 0299 0000

10 0174 0

.( ) . ( ) . ( ) . ( )

.( ) . ( )

RXYZ

º++

º+.().()

.( ) . ( ) . ( ) . ( )

587 0 066

10 0 200 0 114 1111

BXYZ

º++

XRGB

YRGB

=++

0 607 0174 0 200

0299 0587 0114

000

...

. 0 0 066 1111RGB++..

10 1909 0 985 0 058

10 0 532

.(). (). (). ()

.( ) . ( )

XRGB

º-+

º- +1997 0119

10 0 288 0 028 0 902

.().()

.( ) . ( ) . ( ) . (

ZRGB

º- - + )

RXYZ

GXYZ

=--

=- + -

1909 0 532 0 288

0985 1997 0028

...

. 58 0119 0 902XYZ-+..

Уравнения перехода от R – L, L, B – L к XYZ и обратно:

10 0 518 0 000 0 034

10 0981

.( ) . ( ) . ( ) . ( )

.( ) . ( )

CXYZ

º+-

º++

1000 1177

10 0166 0000 1098

.().()

.( ) . ( ) . ( ) . (

CXY

X =-++-

=- -

0 518 0 981 0166

1000

0 034

.( ). .( )

RL L BL

ZRL). . ( )++ -1177 1098LBL

10 1909 0 000 0 058

10 1532

.(). (). (). ()

.( ) . (

XC S C

RCB

º++

º- CSC

ZCS

RCB

). (). ( )

.( ) . ( ) . ( )

º- +

1000 1119

10 0 288 0 000 +0902.()C

RL X Y Z

BL X Y

-= - -

-= - +

1909 1 532 0 288

1000

0 058 1119

...

..0902. Z

Уравнения перехода от E

, E

к E

, E

и обратно:

EEE EE

EEE

IRY BY

QRY

=---

=-+

0 736 0 268

0478 0413

.( ).( )

.( ).(EE

- )

560

ГЛАВА 22 NTSC, PAL И SECAM