Harris C.M., Piersol A.G. Harris Shock and vibration handbook

Подождите немного. Документ загружается.

system is represented by two separate single degree-of-freedom systems, as shown in

Figs. 31.2B and 31.3B, the time-history of F(

δ,δ) is also required. Figure 31.4 may be

considered a generalized form of the applicable system. In Class I, F = 0, F

(

,δ

)

represents the properties of the isolator, and m

(

,δ

) represents the component

to be protected. In Class II, u = 0, F

(

,δ

) represents the properties of the isolator,

and m

(

,δ

) represents the supporting structure.

The system of Fig. 31.4, with the spring-dashpot units nonlinear, requires the use

of a digital computer to investigate performance characteristics. Analytical methods

are feasible if the system is linearized by assuming that each spring-dashpot unit has

a force characteristic in the form

δ,δ) = c

δ+kδ (31.7)

where c = damping coefficient, lb-sec/in., and k = spring stiffness, lb/in. Even with this

simplification, the number of parameters (m

) is so great that it is nec-

essary to confine the analysis to a particular system. If the damping may be neg-

lected [let c = 0 in Eq. (31.7)], then it is feasible to obtain equations in a form suitable

for routine use. Use of this idealization is described in the section on Response of

Equipment with a Flexible Component.

A different form of idealization is indicated when the “equipment” is flexible;

e.g., a large, relatively flexible aircraft subjected to landing shock. Then it is impor-

tant to represent the aircraft as a system with several degrees-of-freedom. To find

resulting stresses, it is necessary to superimpose the responses in the various modes

of motion that are excited.

RESPONSE OF A RIGID BODY SYSTEM

TO A VELOCITY STEP

PHYSICAL BASIS FOR VELOCITY STEP

The idealization of a shock motion as a simple change in velocity (velocity step) may

form an adequate basis for designing a shock isolator and for evaluating its effec-

tiveness. Consider the two types of acceleration ü vs. time t curves illustrated in Fig.

31.5A. The solid line represents a rectangular pulse of acceleration and the dashed

line represents a half-sine pulse of acceleration. Each pulse has a duration τ. In Fig.

31.6 CHAPTER THIRTY-ONE

FIGURE 31.4 General two degree-of-freedom system.

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.6

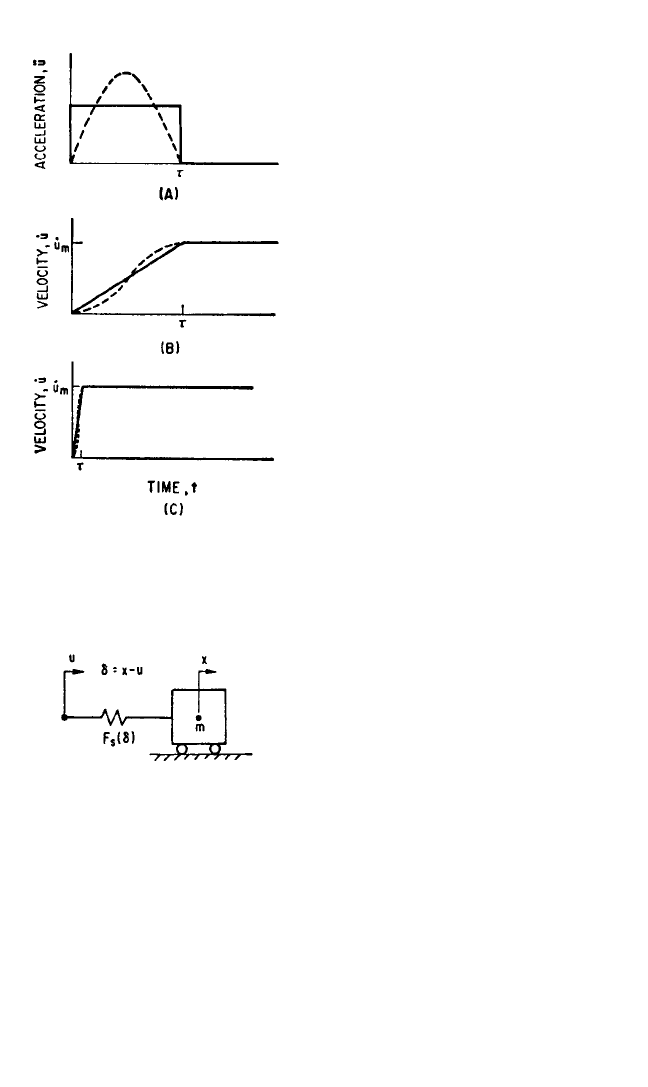
31.5B, the corresponding velocity-time

curves are shown. Each of these curves

is defined completely by specifying the

type of acceleration pulse (rectangular

or half-sine), the duration τ, and the

velocity change

. The curves of Fig.

31.5B are repeated in Fig. 31.5C with the

time scale shrunk to one-tenth. If τ is

sufficiently short, the only significant

remaining characteristic of the velocity

step is the velocity change

. The ideal-

ized velocity step, then, is taken to be a

discontinuous change of

u from zero to

. A shock isolator characteristically

has a low natural frequency (long

period), and this idealization leads to

good results even when the pulse dura-

tion τ is significantly long.

GENERAL FORM OF ISOLATOR

CHARACTERISTICS

The differential equation of motion

for the undamped, single degree-of-

freedom system shown in Fig. 31.6 is

δ+F

(δ) =−mü (31.8)

where m represents the mass of the

equipment considered as a rigid body, u

represents the motion of the support

which characterizes the condition of

shock, and F

(δ) is the force developed

by the isolator at an extension δ (posi-

tive when tensile). Equation (31.8) dif-

fers from Eq. (31.5) in that F

(δ), which

does not depend upon

δ, replaces F(

δ,δ)

because the isolator is undamped. The

effect of a velocity step of magnitude

at t = 0 is considered by choosing the ini-

tial conditions: At t = 0, δ=0 and

δ=

These conditions correspond to a negative velocity step.This choice is made to avoid

dealing with negative values of δ and

δ. If F

(δ) is not an odd function of δ, a positive

velocity step requires a separate analysis.

A first integration of Eq. (31.8) yields

− 

(δ)dδ (31.9)

At the extreme value of isolator deflection, δ=δ

and the velocity

δ of deflection is

zero. Then from Eq. (31.9),



THEORY OF SHOCK ISOLATION 31.7

FIGURE 31.5 Acceleration-time curves (A)

and velocity-time curves (B) and (C) for rect-

angular acceleration pulse (solid curves) and

half-sine acceleration pulse (dashed curves).

FIGURE 31.6 Idealized system showing use of

undamped isolator to protect equipment from

effects of support motion u.

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.7



(δ)dδ=

⁄2m

(31.10)

The right side of Eq. (31.10) represents the initial kinetic energy of the equipment

relative to the support, and the integral on the left side represents the work done on

the isolator. The latter quantity is equal to the elastic potential energy stored in the

isolator, since there is no damping.

For the special case of a rigid body mounted on an undamped isolator, Eq. (31.10)

suffices to determine all important results. In particular, the quantities of engineer-

ing significance are:

1. The maximum deflection of the isolator δ

2. The maximum isolator force, F

= F

(δ

) = m

3. The corresponding velocity change

The interrelations of these three quanti-

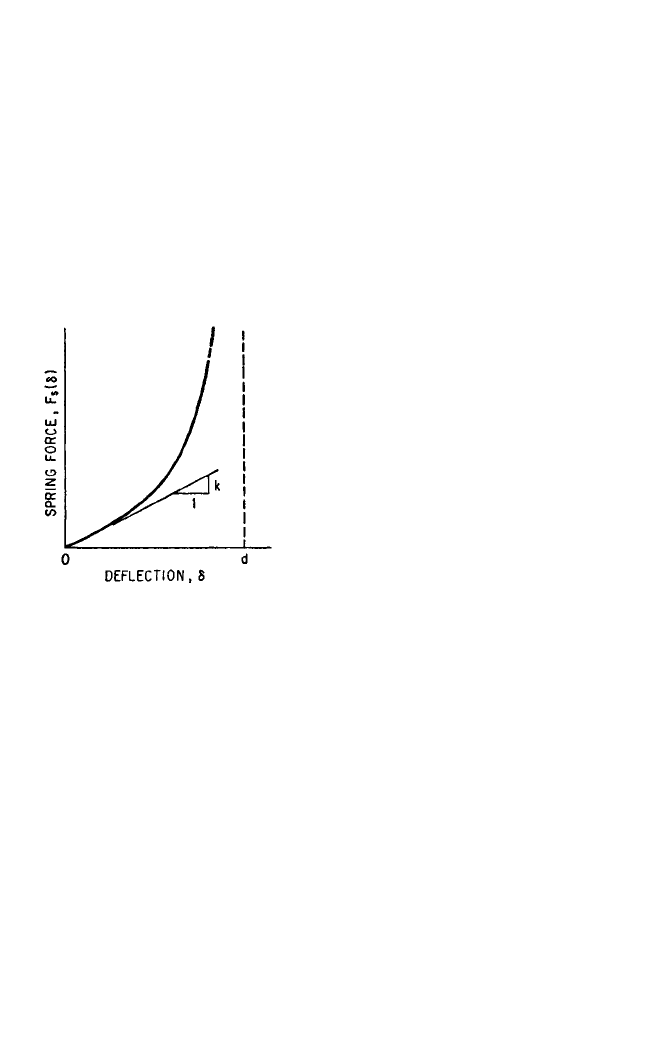
ties are shown graphically in Fig. 31.7.

The curve OAB represents the spring

force F

(δ) as a function of deflection δ.

If point A corresponds to the extreme

excursion, then its abscissa represents

the maximum deflection δ

. The shaded

area OAC is proportional to the poten-

tial energy stored by the isolator;

according to Eq. (31.10), this is equal to

the initial kinetic energy m

/2. The

maximum ordinate (at A) represents the

maximum spring force F

. [It is possible

to have a spring force F

(δ) which attains

a maximum value at δ=δ

<δ

. Then

= F

(δ

).]

The design requirements for the isolator usually include as a specification one or

more of the following quantities:

1. Maximum allowable deflection δ

2. Maximum allowable transmitted force F

3. Maximum expected velocity step

It is important to observe that the limits 1 and 2 establish an upper limit F

on the

work done on the mass. It follows that

must satisfy the relation

≥ m

or the specifications are impossible to meet. The specifications may be expressed

mathematically as follows:

≤δ

≤ F

≥

(31.11)

In many instances it is advantageous to eliminate explicit reference to the mass

m. Then the allowable absolute acceleration

of the mass is specified instead of the

31.8 CHAPTER THIRTY-ONE

FIGURE 31.7 Typical force-deflection curve

for undamped isolator.

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.8

allowable force F

where F

= m

. With this substitution the second of Eqs. (31.11)

is replaced by

≤

(31.12)

The acceleration

x is determined as a function of time by using

δ from Eq. (31.9) and

finding the time t corresponding to a given value of δ:

t =



(31.13)

From Eq. (31.13) and the relation

x = F

(δ)/m, the acceleration time-history is

found.

The integrations required by Eqs. (31.9) and (31.13) sometimes are difficult to

perform, and it is necessary to use numerical methods. Then a difficulty arises with

the integral in Eq. (31.13). As δ approaches the extreme value δ

, the velocity

δ in

the denominator of the integrand approaches zero. The difficulty is circumvented by

first using Eq. (31.13) to integrate up to some intermediate displacement δ

less than

; then the alternative form, Eq. (31.14), may be used in the region of δ=δ

t = t

+ 

(31.14)

where t

is the time at which δ=δ

, as determined from Eq. (31.13).

In the next three sections three different kinds of spring force-deflection charac-

teristics F

(δ) are considered. Equation (31.10) is applied to find the relation

between

and δ

. Curves relating

, δ

, and

in a form useful for design or analy-

sis are presented.

EXAMPLES OF PARTICULAR ISOLATOR CHARACTERISTICS

Linear Spring. The force-deflection characteristic of a linear spring is

(δ) = kδ (31.15)

where k = spring stiffness, lb/in. Using the notation



rad/sec (31.16)

the maximum acceleration is

=ω

(31.17)

From Eqs. (31.10) and (31.16), the relation between velocity change

and maxi-

mum deflection δ

=ω

(31.18)

Combining Eqs. (31.18) and (31.17),

=ω

(31.19)



dδ



THEORY OF SHOCK ISOLATION 31.9

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.9

Hardening Spring (Tangent Elasticity). The isolator spring may be nonlinear

with a “hardening” characteristic; i.e., the slope of the curve representing spring

force vs. deflection increases with increasing deflection. Rubber in compression has

this behavior.A representative curve having this characteristic is defined by

(δ) = tan (31.20)

where the constant k is the initial slope of the curve (lb/in.) and a vertical asymptote

is defined by δ=d (in.). Such a curve is shown graphically in Fig. 31.8. Using the

notation of Eq. (31.16) and the relation m

= F

(δ

), Eq. (31.20) gives the following

relation between maximum acceleration and maximum deflection:

= tan (31.21)

Note that ω

, the angular natural fre-

quency for a linear system, has the same

meaning for small amplitude (small δ

)

motions of the nonlinear system. For

large amplitudes the natural frequency

depends on δ

. Using Eq. (31.16), substi-

tuting for F

(δ) from Eq. (31.20) in Eq.

(31.10), and performing the indicated

integration, the relation between veloc-

ity change and maximum displacement

= log



sec



(31.22)

A graphical presentation relating the

important variables

, and δ

is con-

venient for design and analysis. Such data are presented compactly as relations

among the dimensionless parameters δ

/d,

/ω

d, and

.The physical signif-

icance of the ratio

is interpreted by multiplying both numerator and

denominator by m. Then the numerator represents the product of the maximum

spring force F

(= m

) and the maximum spring deflection δ

. This product is the

maximum energy that could be stored in the spring. The denominator m

is twice

the energy that is stored in the spring. The minimum possible value of the ratio

⁄2. Actual values of the ratio, always greater than

⁄2, may be considered to

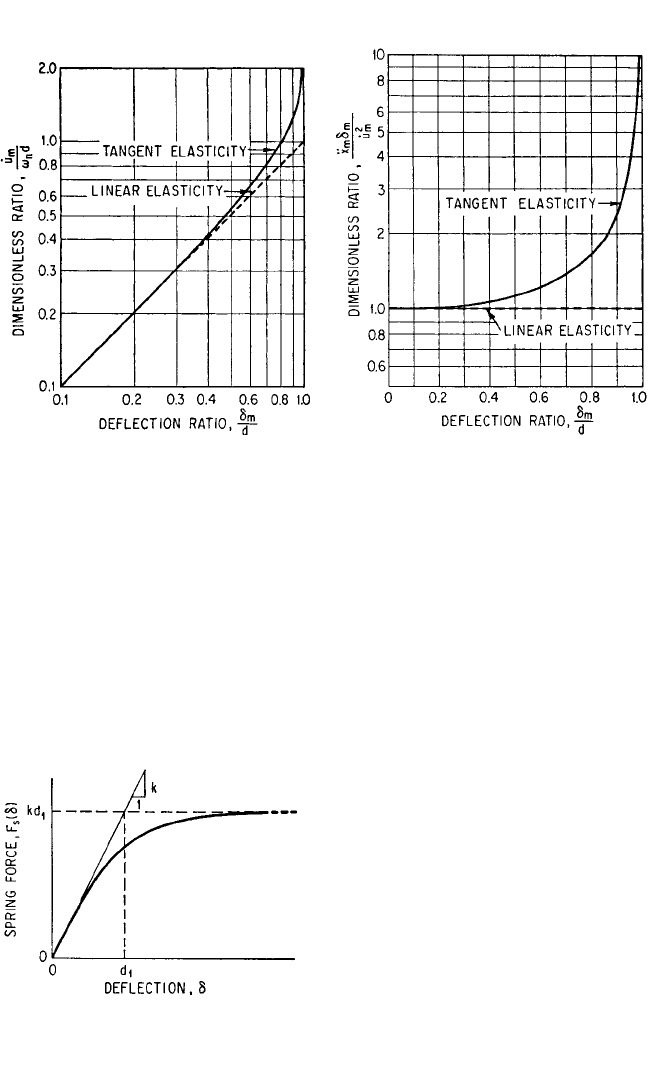
be a measure of the departure from optimum capability.

In Fig. 31.9 the solid curve represents

/ω

d as a function of δ

/d and the dashed

curve shows the corresponding result for a linear spring [see Eq. (31.18)]. In Fig.

31.10 the solid curve shows

vs. δ

/d for an isolator with tangent elasticity.

The dashed curve in Fig. 31.10 shows

for a linear spring [see Eqs. (31.17)

and (31.18)]; the ratio is constant at a value of unity because a linear spring is 50 per-

cent efficient in storage of energy, independent of the deflection.

Softening Spring (Hyperbolic Tangent Elasticity). A nonlinear isolator also

may have a “softening” characteristic; i.e., the slope of the curve representing force

πδ



πδ



πδ



2kd



31.10 CHAPTER THIRTY-ONE

FIGURE 31.8 Typical force-deflection curve

for hardening spring (tangent elasticity).

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.10

vs. deflection decreases with increasing deflection. The force-deflection characteris-

tic for a typical “softening” isolator is

(δ) = kd

tanh (31.23)

where k is the initial slope of the curve. Figure 31.11 shows the form of this curve

where the meaning of d

is evident from the figure. If F

(δ) is replaced by m

, δ by

, and k by mω

, Eq. (31.23) becomes

= tanh (31.24)

where δ

and

are maximum values of

deflection and acceleration, respec-

tively, and ω

may be interpreted as the

angular natural frequency for small val-

ues of δ

. To relate

to δ

, substitute

(δ) from Eq. (31.23) in Eq. (31.10), let

= k/m, and integrate:

= log



cosh



(31.25)

A graphical presentation of the rela-

tion between

/ω

and δ

is given



THEORY OF SHOCK ISOLATION 31.11

FIGURE 31.9 Dimensionless representation

of relation between velocity step

and maxi-

mum isolator deflection δ

for undamped iso-

lators.

FIGURE 31.10 Dimensionless representation

of relation among velocity step

, maximum

transmitted acceleration

, and maximum isola-

tor deflection δ

for undamped isolators.

FIGURE 31.11 Typical force-deflection curve

for softening spring (hyperbolic tangent elas-

ticity).

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.11

by the solid curve of Fig. 31.12. The dashed curve shows the corresponding relation

for a linear spring. In Fig. 31.13 the solid curve represents

as a function of

. Note that, for large values of δ

, the ordinate approaches the minimum

value

⁄2 attainable with an isolator of optimum energy storage efficiency.The dashed

curve shows the same relation for a linear spring.

Linear Spring and Viscous Damping. The addition of viscous damping can

almost double the energy absorption capability of a linear shock isolator. Consider

the system of Fig. 31.2A, with both spring and dashpot linear as defined by Eq.

(31.7). Substituting F(

δ,δ) from Eq. (31.7) in Eq. (31.5) gives the equation of motion.

The initial conditions are

δ=

, δ=0, when t = 0; for t > 0, ü = 0. Letting c

= 2mω

and ζ=c/c

[see Eq. (2.12)], the equation of motion becomes

δ+2ζω

δ+ω

δ=0 (31.26)

Solutions of Eq. (31.26) for maximum deflection δ

and maximum acceleration

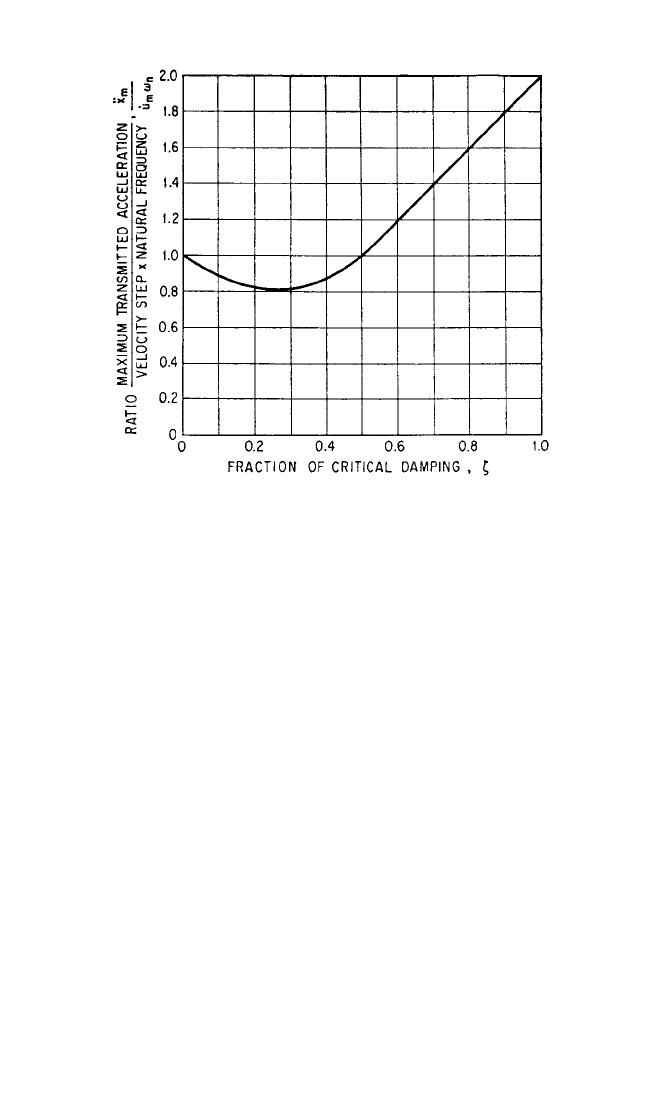
functions of ζ are shown graphically in Figs. 31.14 and 31.15. In Fig. 31.14, the dimen-

sionless ratio

is plotted as a function of the fraction of critical damping ζ.

Note that the presence of small damping reduces the maximum acceleration. As ζ is

increased beyond 0.25, the maximum acceleration increases again. For ζ>0.50, the

maximum acceleration occurs at t = 0 and exceeds that for no damping; it is

accounted for solely by the damping force c

δ=c

31.12 CHAPTER THIRTY-ONE

FIGURE 31.12 Dimensionless representation

of relation between velocity step

and maxi-

mum isolator deflection δ

for undamped iso-

lators.

FIGURE 31.13 Dimensionless representation

of energy-storage capabilities of undamped iso-

lators.

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.12

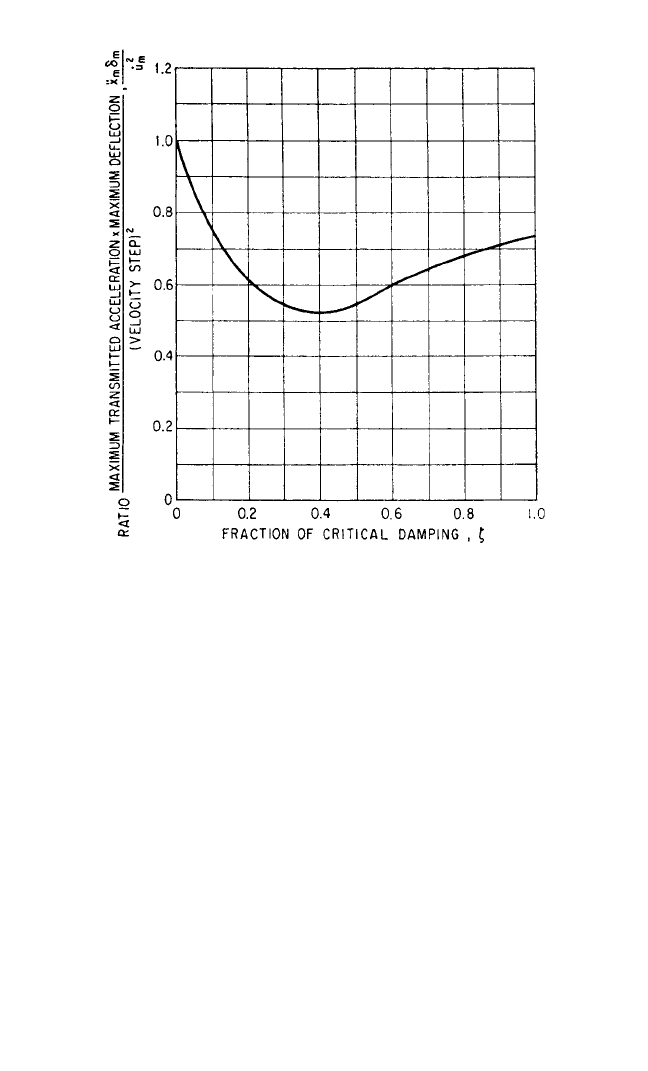
In Fig. 31.15 the parameter

is plotted as a function of ζ. (As pointed out

with reference to Fig. 31.10,

is an inverse measure of shock isolator effective-

ness.) Figure 31.15 shows that the presence of damping improves the energy storage

effectiveness of the isolator even beyond ζ=0.50. In the neighborhood ζ=0.40, the

parameter

attains a minimum value of 0.52—only slightly above the theoret-

ical minimum of 0.50. This parameter has the value 1.00 for an undamped linear sys-

tem, and even higher values for a hardening spring (see Fig. 31.10). On the other hand,

may approach 0.50 when a softening spring is used.

True viscous damping of the type considered above is difficult to attain except in

electrical or magnetic form. Fluid dampers which depend upon orifices or other con-

stricted passages to throttle the flow are likely to produce damping forces that vary

more nearly as the square of the velocity. Dry friction tends to provide damping

forces which are virtually independent of velocity. The analysis of response to a

velocity step in the presence of Coulomb friction is similar to that described in the

section entitled General Formulas—No Damping.

Example 31.1. Equipment weighing 40 lb and sufficiently stiff to be considered

rigid is to be protected from a shock consisting of a velocity step

= 70 in./sec. The

maximum allowable acceleration is

= 21g (g is the acceleration of gravity) and

available clearance limits the deflection to δ

= 0.70 in. Find isolator characteristics

for: linear spring, hardening spring, softening spring, and linear spring with viscous

damping.

Linear Spring. Taking the maximum velocity

equal to the expected velocity

and using Eqs. (31.18) and (31.11),

THEORY OF SHOCK ISOLATION 31.13

FIGURE 31.14 Dimensionless representation of maximum trans-

mitted acceleration

for an isolator having a linear spring and vis-

cous damping.

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.13

=≤δ

or ω

≥=100 rad/sec

From Eqs. (31.19) and (31.12),

=ω

≤

. Then

≤= =116 rad/sec

Selecting a value in the middle of the permissible range gives ω

= 108 rad/sec [17.2

Hz]. The corresponding maximum isolator deflection is δ

= 0.65 in. and the maxi-

mum acceleration of the equipment is

= 7580 in./sec

= 19.6g.The isolator stiffness

given by Eq. (31.16) is

k = mω

=×(108 rad/sec)

= 1210 lb/in.

If, as is usually the case, the isolation is provided by several individual isolators in

parallel, then the above value of k represents the sum of the stiffnesses of the indi-

vidual isolators.

Hardening Spring. The tangent elasticity represented by Eq. (31.20) is

assumed. Since the linear spring meets the specifications with only a small margin of

40 lb



386 in./sec

21 × 386 in./sec



70 in./sec



70 in./sec



0.70 in.



31.14 CHAPTER THIRTY-ONE

FIGURE 31.15 Dimensionless representation of energy absorption

capability of an isolator having a linear spring and viscous damping.

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.14

safety, it is inferred that the poorer energy storage capacity of the hardening spring

shown by Fig. 31.10 will severely limit the permissible nonlinearity. Using the speci-

fied values as maxima,

== =1.16

From Fig. 31.10:

= 0.54; thus d ==1.30 in.

From Fig. 31.9:

= 0.58; thus ω

==93 rad/sec [14.8 Hz]

The initial spring stiffness k from Eq. (31.16) is

k = (93)

= 896 lb/in.

Because the selected linear spring provides a small margin of safety and the hard-

ening spring provides none, superficial comparison suggests that the former is supe-

rior. Various other considerations, such as compactness and stiffness along other

axes, may offset the apparent advantage of the linear spring. Moreover, a shock

more severe than that specified could cause the linear spring to bottom abruptly and

cause much greater acceleration of the equipment.

Softening Spring. The hyperbolic tangent elasticity represented by Eq. (31.23)

is assumed. The softening spring has high energy-storage capacity as shown by

Fig. 31.13. By working to sufficiently high values of δ

, it is possible to utilize this

storage capacity to afford considerable overload capability. Choose

= 20g and

= 3. From Fig. 31.13,

= 0.645 at δ

= 3. Then

= 0.645 = 0.41 in. d

==0.137 in.

From Fig. 31.12,

/ω

= 2.15 at δ

= 3. Then

==238 rad/sec [37.9 Hz]

The initial spring stiffness k from Eq. (31.16) is

k = (238)

= 5870 lb/in.

This initial stiffness is much greater than those found for the linear spring and

hardening spring.Accordingly, for small shocks (small

) the isolator with the soft-

ening spring will induce much higher acceleration of the equipment than will those



386



2.15 × 0.137



(70)



20 × 386



386



1.30 × 0.54



0.70



0.54



(21 × 386) × 0.70



(70)



THEORY OF SHOCK ISOLATION 31.15

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.15